SỞ GIÁO DỤC ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 ĐĂK NÔNG
NĂM HỌC: 2023 – 2024 Môn: TOÁN
Khoá thi ngày: 8/6/2022
Thời gian làm bài: 120 phút (không kể thời gian giao đề) Câu 1. (2,0 điểm)
a) Tính giá trị biểu thức: A  27  3  12 . 2 2 x  9 x  2x
b) Rút gọn biểu thức: B  
 x  2; x  3   . x  3 x  2 Câu 2. (2,0 điểm)
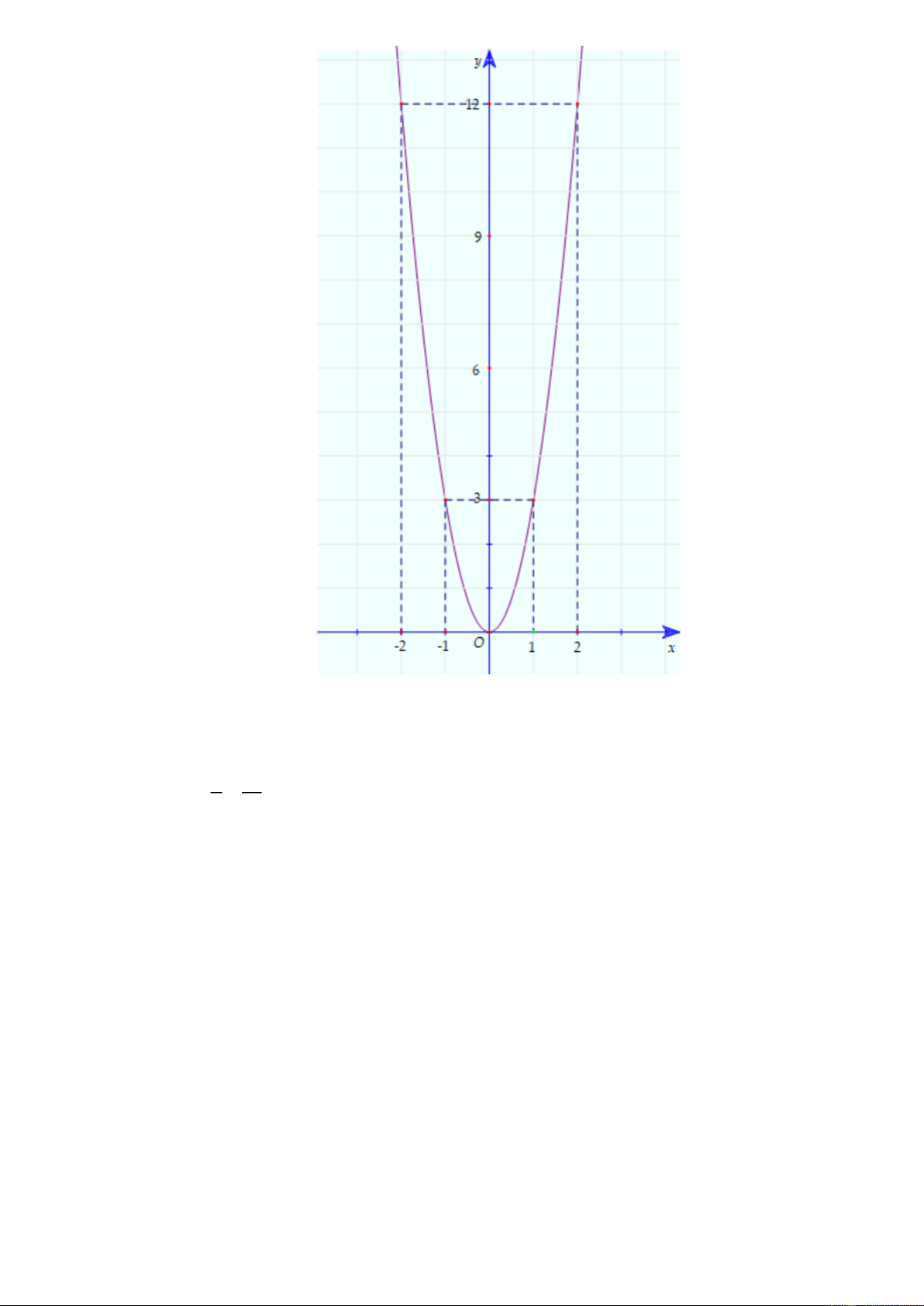
a) Vẽ đồ thị của hàm số  P 2 : y  3x .
b) Giải phương trình bậc hai: 2
x  5x  6  0 . Câu 3. (2,0 điểm) 3
 x  2y  5
a) Giải hệ phương trình bậc nhất hai ẩn:  .
x  2y  7
b) Để làm hoa viên, do đất trũng nên Thành phố Gia Nghĩa lên kế hoạch đổ 2000 xe đất trong
một thời gian quy định. Nhờ giao thông thuận lợi nên mỗi ngày đội thi công đổ được thêm 50
xe đất. Vì thế đội thi công hoàn thành sớm hơn kế hoạch là 2 ngày. Hỏi theo kế hoạch, mỗi
ngày đội thi công cần đổ được bao nhiêu xe đất?
Câu 4. (3,0 điểm) Cho tam giác ABC có ba góc nhọn  AB  AC nội tiếp đường tròn tâm O , đường
cao BE, CF cắt nhau tại H .
a) Chứng minh tứ giác BCEF nội tiếp.
b) Chứng minh BF .CA  BH .CF . AH
c) Gọi K là trung điểm của đoạn thẳng BC . Tính tỉ số . OK
Câu 5. (1,0 điểm) Cho các số thực x, y thỏa mãn 5
x  y  xy 
. Tìm giá trị nhỏ nhất của biểu thức 4 2 2
P  x  y .
---------------------------------@Hết@--------------------------------- Trang 1 HƯỚNG DẪN GIẢI Câu 1. (2,0 điểm)
a) Tính giá trị biểu thức: A  27  3  12 . 2 2 x  9 x  2x
b) Rút gọn biểu thức: B  
 x  2; x  3   . x  3 x  2 Lời giải
a) Tính giá trị biểu thức: A  27  3  12 . A 
27  3  12  3 3  3  2 3  4 3 2 2 x  9 x  2x
b) Rút gọn biểu thức: B  
 x  2; x  3   . x  3 x  2 2 2 x  9 x  2x
x 3x 3 xx  2 B    
 x  3 x  2x  3 . x  3 x  2 x  3 x  2 Câu 2. (2,0 điểm)
a) Vẽ đồ thị của hàm số  P 2 : y  3x .
b) Giải phương trình bậc hai: 2
x  5x  6  0 . Lời giải
a) Vẽ đồ thị của hàm số  P 2 : y  3x . x 2  1 0 1 2 2 y  3x 12 3 0 3 12 Trang 2
b) Giải phương trình bậc hai: 2
x  5x  6  0 .
Ta có: a  b  c  ( 1  )  ( 5  )  6  0 x 1 1    c 6 . x    6   2  a 1  Câu 3. (2,0 điểm) 3
 x  2y  5
a) Giải hệ phương trình bậc nhất hai ẩn:  .
x  2y  7
b) Để làm hoa viên, do đất trũng nên Thành phố Gia Nghĩa lên kế hoạch đổ 2000 xe đất trong
một thời gian quy định. Nhờ giao thông thuận lợi nên mỗi ngày đội thi công đổ được thêm 50
xe đất. Vì thế đội thi công hoàn thành sớm hơn kế hoạch là 2 ngày. Hỏi theo kế hoạch, mỗi
ngày đội thi công cần đổ được bao nhiêu xe đất? Lời giải 3
 x  2y  5
a) Giải hệ phương trình bậc nhất hai ẩn:  .
x  2y  7 3
 x  2y  5 4x 12 x  3 x  3        .
x  2y  7
x  2y  7 3   2y  7 y  2  x  3
Vậy hệ phương trình có nghiệm duy nhất  . y  2 
b) Để làm hoa viên, do đất trũng nên Thành phố Gia Nghĩa lên kế hoạch đổ 2000 xe đất trong Trang 3
một thời gian quy định. Nhờ giao thông thuận lợi nên mỗi ngày đội thi công đổ được thêm 50
xe đất. Vì thế đội thi công hoàn thành sớm hơn kế hoạch là 2 ngày. Hỏi theo kế hoạch, mỗi
ngày đội thi công cần đổ được bao nhiêu xe đất?
Gọi số xe đất mỗi ngày cần đổ theo kế hoạch là x  * x .
Thực tế mỗi ngày đổ được số xe đất là x  50 (xe đất). 2000
Theo kế hoạch số ngày đổ đất là: (ngày) x 2000
Thực tế số ngày đổ đất là: (ngày) x  50
Vì số ngày đổ đất thực tế sớm hơn kế hoạch là 2 ngày nên ta có phương trình: 2000 2000 2 
 2  2000x 100 000  2000x  2x 100x x x  50 2
 x  50x  50 000  0 Ta có: 2 2 
  b  ac  25 1. 5  0 000  50 625 Vì 
  0 nên phương trình có 2 nghiệm phân biệt b
    25  50625 25  225 x     200 (thỏa mãn) 1 a 1 1
b   25  50625 25   225 x   
 250 (không thỏa mãn). 2 a 1 1
Vậy theo kế hoạch, mỗi ngày đội thi công cần đổ 200 xe đất.
Câu 4. (3,0 điểm) Cho tam giác ABC có ba góc nhọn  AB  AC nội tiếp đường tròn tâm O , đường
cao BE, CF cắt nhau tại H .
a) Chứng minh tứ giác BCEF nội tiếp.
b) Chứng minh BF .CA  BH .CF . AH
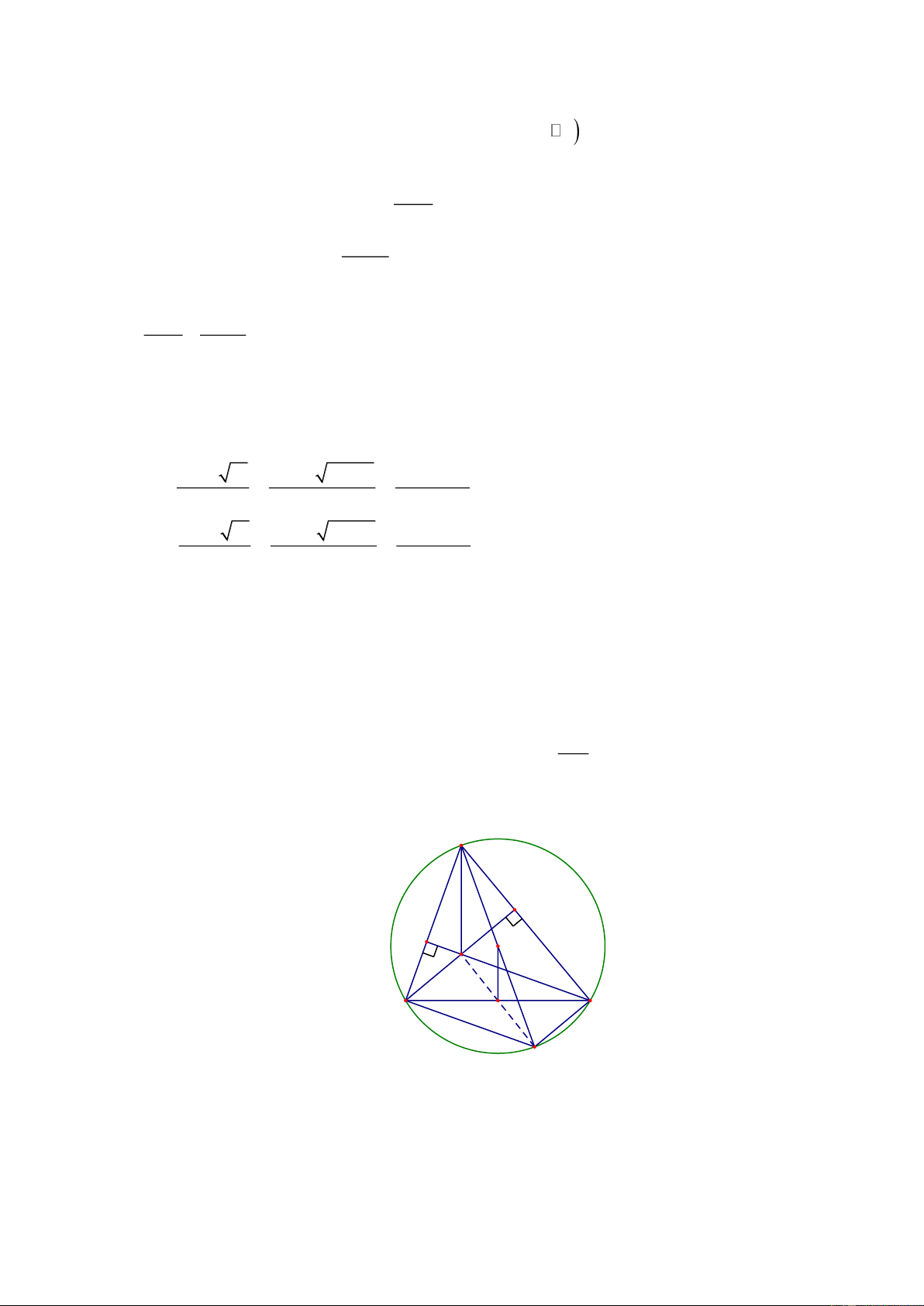
c) Gọi K là trung điểm của đoạn thẳng BC . Tính tỉ số . OK Lời giải A E F O H B K C I
a) Chứng minh tứ giác BCEF nội tiếp.
Xét tứ giác BCEF có:
BFC  90 ( CF là đường cao)
BEC  90 ( BE là đường cao)
 BFC  BEC  90 Trang 4
mà F và E là 2 đỉnh kề nhau cùng nhìn cạnh BC
 Tứ giác BCEF nội tiếp.
b) Chứng minh BF .CA  BH .CF .
Ta có: tứ giác BCEF nội tiếp (chứng minh câu a)
 FBH  FCA (hai góc nội tiếp cùng chắn cung FE ) Xét FBH  và F  CA có:
BFH  CFA  90
FBH  FCA (chứng minh trên)  F  BH # F
 CA g.g BF BH  
 BF .CA  BH .CF . CF CA AH
c) Gọi K là trung điểm của đoạn thẳng BC . Tính tỉ số . OK
Kẻ đường kính AI của đường tròn tâm O  ABI  ACI  90 C  H // BI   AB  
 Tứ giác BHCI là hình bình hành BH // CI   AC
mà K là trung điểm của BC  K là trung điểm HI . Xét A
 HI có: O là trung điểm của AI và K là trung điểm HI
OK là đường trung bình của A  HI 1  AH OK  AH hay  2 . 2 OK
Câu 5. (1,0 điểm) Cho các số thực x, y thỏa mãn 5
x  y  xy 
. Tìm giá trị nhỏ nhất của biểu thức 4 2 2
P  x  y . Lời giải
Ta có:  x  y2 2 2
 0  x  y  2xy        2 2 2 2 x y x
y và  x  y2  4xy . 5
Ta có: x  y  xy 
 5  4x  y  4xy  4x  y  x  y2 . 4
 x  y2  4x  y 5  0  x  y  
1  x  y  5  0  x  y  1
x  y2 1     . x  y  5 
x  y2  25 2 1 2 1 Ta có: 2 2 2
x  y    x  y  P   x  y  . 2 2 x  y 1 Dấu “=” xảy ra khi 
 x  y  . x  y  1 2 1 1
Vậy giá trị nhỏ nhất của P  khi x  y  . 2 2
---------------------------------@Hết@--------------------------------- Trang 5