Đề thi tuyển sinh 10 THPT năm 2023-2024 toán chuyên Sở GD Hải Dương (có đáp án và lời giải chi tiết)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 TRUNG HỌC PHỔ THÔNG HẢI DƯƠNG
NĂM HỌC 2023 – 2024
Môn thi: TOÁN (chuyên) Ngày thi: 03/06/2023 ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút, không tính thời gian phát đề Đề thi có 01 trang Câu 1 (2,0 điểm)
1. Cho hai số a, b thoả mãn các điều kiện .
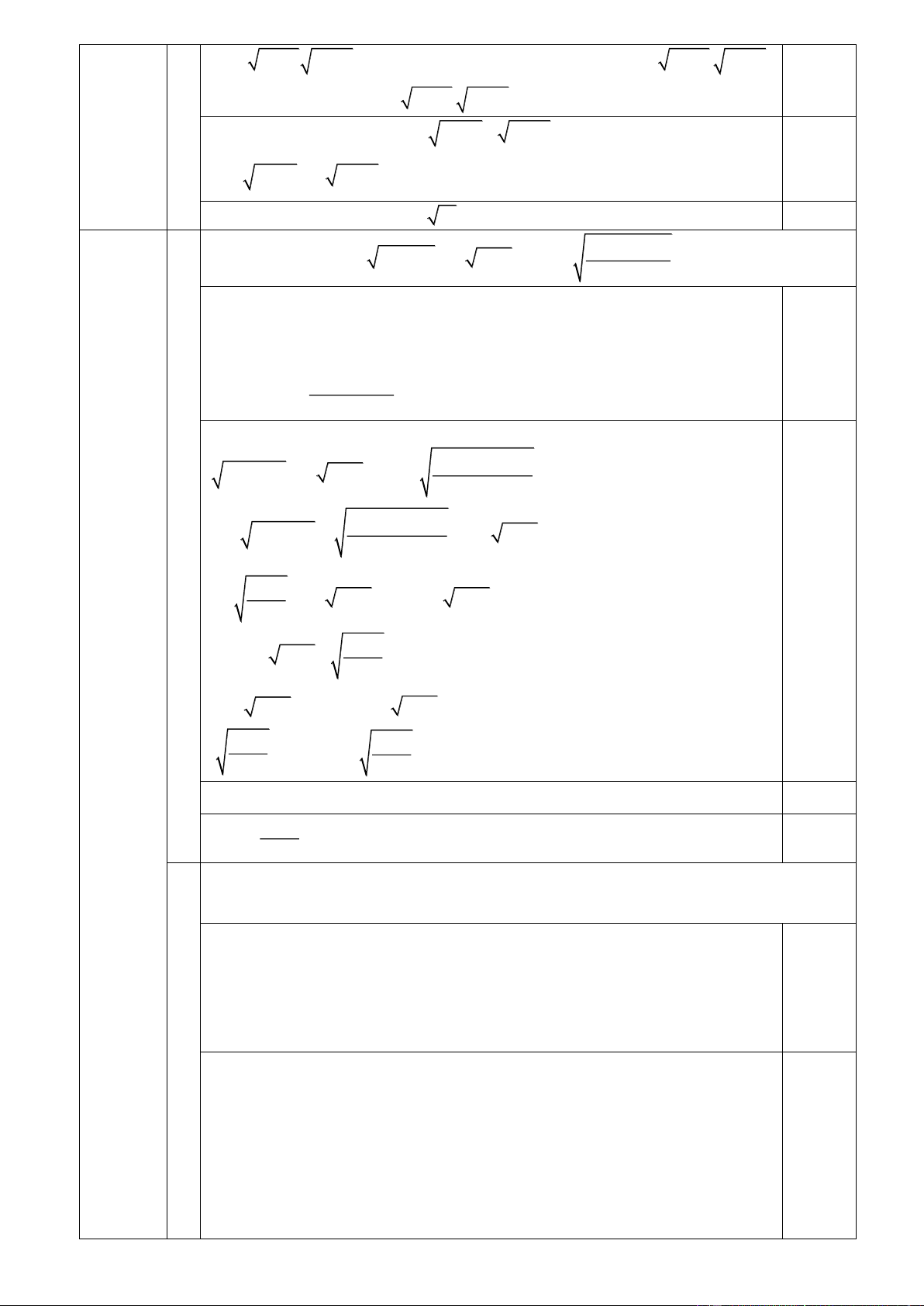
a b = 1, a + b ¹ 0 . Rút gọn biểu thức: 1 æ1 1 ö 3 æ1 1 ö 6 Q ç ÷ ç ÷ = + + ç ÷ + + ç ÷ ç ÷ è ø ç ÷ (a b)3 3 3 a b (a + b + )2 2 2 2 2 2 èa b ø + (a + b)4 2. Cho hai số dương , x y thoả mãn 2 2
x y 1  y x 1  15 . Tính giá trị của biểu thức: P   2
x   x 2 1
y 1  y  Câu 2 (2,0 điểm) 2 x + 2x - 3 1. Giải phương trình: 2
x + 3x + 2 x - 1 = 2x + x
ìï xy + 2x + y = 2 ï
2. Giải hệ phương trình: í 2 2
ï x + y + 2x + 4y = 3 ïî Câu 3 (2,0 điểm)
1. Tìm tất cả các số nguyên tố p lẻ sao cho 4 2
2 p - p + 16 là số chính phương.
2. Tìm nghiệm nguyên của phương trình 2 2
6x + 7xy + 2 y + x + y - 2 = 0 . Câu 4 (3,0 điểm)
1. Cho tam giác đều ABC nội tiếp đường tròn O , điểm E thuộc cung nhỏ AB của
đường tròn O E  ,
A E  B . Đường thẳng AE cắt các tiếp tuyến tại B,C của đường tròn
O lần lượt tại M, N . a) Chứng minh rằng 2 M . B NC  AB .
b) Gọi F là giao điểm của MC và BN , H là trung điểm BC . Chứng minh rằng ba điểm
E, F , H thẳng hàng.
2. Cho đường tròn (O) và hai điểm ,
A B cố định nằm trên đường tròn (O) sao cho · 0
AOB = 120 . Điểm M thay đổi trên cung lớn »
AB của đường tròn (O). Đường tròn nội tiếp
tam giác MAB tiếp xúc với M ,
A MB lần lượt tại E, F . Chứng minh rằng đường thẳng EF luôn
tiếp xúc với một đường tròn cố định. Câu 5 (1,0 điểm)
Cho a,b, c là các số không âm và không có hai số nào đồng thời bằng 0 . Chứng minh rằng: 1 1 1 10 + + ³ 2 2 2 2 2 2 a + b b + c c + a
(a + b + c)2 ---------HẾT--------- Họ và tên thí sinh:
………………………………………… Số báo danh:
………………………………
Cán bộ coi thi số 1 …………………………………………Cán bộ coi thi số 2 ………………………. Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM HẢI DƯƠNG
KỲ THI TUYỂN SINH LỚP 10 TRUNG HỌC PHỔ THÔNG
NĂM HỌC 2023 – 2024
Môn thi: TOÁN (chuyên)
(Hướng dẫn chấm có 05 trang) Câu Ý Nội dung Điểm
Cho hai số a, b thoả mãn các điều kiện .
a b = 1, a + b ¹ 0 . Rút gọn biểu thức: 1 æ1 1 ö 3 æ1 1 ö 6 Q ç ÷ ç ÷ = + + ç ÷ + + ç ÷ ç ÷ è ø ç ÷ (a b)3 3 3 a b (a + b + )2 2 2 2 2 2 èa b ø + (a + b)4 Ta có: a + b + = (a + b)2 2 2 2 Nên 1 æ1 1 ö 3 æ1 1 ö 6 Q ç ÷ ç ÷ = + + ç ÷ + + ç ÷ ç ÷ è ø ç ÷ (a b)3 3 3 a b (a b)4 2 2 èa b ø + + (a + b)4 0,25 3 + ( 2 2 3 3 a + b a b ) 6 = + + (a + b)3 (a + b)4 (a + b)4 ( 3 3
a + b )(a + b)+ 3( 2 2 a + b )+ 6 = (a + b)4 4 4 2 2 2 2 1
a + b + ab(a + b )+ 3(a + b )+ 6 = (a + b + )2 2 2 2 0,25 4 4 a + b + 4( 2 2 a + b )+ 6 1 = 2 2 2 (2 điểm) (a + b + ) 2 ( 4 4 2 2
a + b + 2a b )+ 4( 2 2 a + b )+ 4 = (a + b + )2 2 2 2 0,25 (a + b )2 2 2 + 4( 2 2 a + b )+ 4 = (a + b + )2 2 2 2 (a + b + )2 2 2 2 = (a + b + )2 2 2 2 0,25 = 1 Cho hai số dương , x y thoả mãn 2 2
x y 1  y x 1  15 . Tính giá trị của biểu thức: P   2
x   x 2 1
y 1  y 2 2 2 P  x 
y   xy   2 2
x y   y x   2 2 1 1 1 1 
x 1 y 1  xy  15 0,25 Đặt 0,25 Trang 2 2 2 2 M 
x 1 y 1  xy  M   2 x   1  2 y   2 2 2 2
1  x y  2xy x 1. y 1 2 2 2 2 2 2
 2x y  x  y 1 2xy x 1. y 1 2  x  2 y   2 1  y  2 x   2 2
1  2x y 1.y x 1 1 0,25
 x y 1 y x 12 2 2 1
16  M  4 . Vậy P  4  15 . 0,25 2 x + 2x - 3 Giải phương trình: 2
x + 3x + 2 x - 1 = 2x + x ìïïï 2 ï x + 3x ³ 0 ï Điề ï u kiện: í x - 1³ 0 Û x ³ 1 ï 0,25 ï 2 ï x + 2x - 3 ïï ³ 0 ïïî x Phương trình trở thành (x - ) 1 (x + ) 3 x(x + )
3 + 2 x - 1 - 2x - = 0 x æ ç ( ö x - ) 1 (x + ) 3 ÷ Û ç x ç (x + ) 3 ÷ - + ÷ ç
÷ (2 x - 1- 2x)= 0 1 ç x ÷ è ø x + 3 Û (x- x- ) 1 - 2(x - x - ) 1 = 0 0,25 x æ ö Û ( + ç ÷ x - x - ) x 3 1 ç - 2÷= 0 ç ÷ çè x ÷ø é é x - x - 1 = 0 x = x - 1 ( ) 1 ê ê 2 ê ê Û (2 điểm) ê x + 3 ê x + 3 ê - 2 = 0 ê = 2(2) êë x êë x ( ) 2 2
1 Û x = x - 1 Û x - x + 1= 0 (vô nghiệm) 0,25 x + 3 (2)Û
= 4 Û x + 3 = 4x Û x = 1 (Thoả mãn điều kiện) 0,25 x
ìï xy + 2x + y = 2 ï
Giải hệ phương trình: í 2 2
ï x + y + 2x + 4y = 3 ïî ìï (x + ) 1 (y + 2)= 4 ï
Hệ phương trình đã cho trở thành í ïï(x + )2 1 + (y + 2)2 = 8 ïî 0,25 ìï a = x + 1 ìï . a b = 4 Đặ ï t ïí ta được hệ í ï b = y + 2 ïî 2 2 ï a + b = 8 ïî 2 ìï ab = 4 ìï ab = 4 ï ï Û í Û í
ïï(a b)2 2ab 8 ï + - = î ï (a + b)2 = 16 î éìï ab = 4 ï ìï ab = 4 êí ( ) 1 ï ê 0,25 ï ï a + b = 4 ï ïîê Û í a é + b = 4 Û ê ï ê ì ï ïê ab = 4 ï a ê + b = - 4 ï ïî ë íê (2) ïê a + b = - 4 ïîë Trang 3 ìï a = 2 ìï x = 1 ( ) ï ï 1 Û í Þ í ï 0,25 b = 2 ï y = 0 ïî ïî ìï a = - 2 ìï x = - 3 ( ï ï 2)Û í Þ í ï 0,25 b = - 2 ï y = - 4 ïî ïî
Tìm tất cả các số nguyên tố p lẻ sao cho 4 2
2 p - p + 16 là số chính phương. Đặt 4 2
A = 2 p - p + 16 Với p = 3 thì 2
A = 169 = 13 là số chính phương. Vậy p = 3 thoả 0,25 mãn. 1 2 Với p > 3 thì 2 p º ( 1 mod ) 3 . Suy ra 4 p = ( 2 p ) º ( 1 mod ) 3 0,25 Suy ra 4 2
A = 2 p - p + 16 º 2.1- 1+ 16 º 2(mod ) 3 0,25
Do các số chính phương chia cho 3 chỉ dư 0 hoặc 1 nên A không là 0,25 số chính phương.
Tìm nghiệm nguyên của phương trình 2 2
6x + 7xy + 2 y + x + y - 2 = 0 . Ta có phương trình 3 2 2
6x + 7xy + 2 y + x + y - 1= 1 (2 điểm) 2 Û 0,25 6x + (7 y + ) 2
1 x + 2 y + y - 1= 1 Û (2x + y + ) 1 (3x + 2 y - ) 1 = 1
2x  y 1 1    1 2 3
 x  2y 1  1  0,25
2x  y 1  1  2  3
 x  2y 1  1    x  2  1   0,25  y  4   x  4 2   0,25  y  6
1. Cho tam giác đều ABC nội tiếp đường tròn O , điểm E thuộc cung
nhỏ AB của đường tròn O E  ,
A E  B . Đường thẳng AE cắt các tiếp
tuyến tại B,C của đường tròn O lần lượt tại M , N . a) Chứng minh rằng 2 M . B NC  AB . N A E 4 M (3 điể 1 m) O F B C I H Ta có 0
ABM  ACB  BAC  60  BM / / AC  BMA  CAN   1 0,25
Tương tự ta có CN / / AB  BAM  CNA 2 0,25
Từ (1) và (2) ta có A
 MB đồng dạng N  AC (g-g) 0,25 Trang 4 MB AB 2    M . B NC  . AB AC  M . B NC  AB 0,25 AC NC
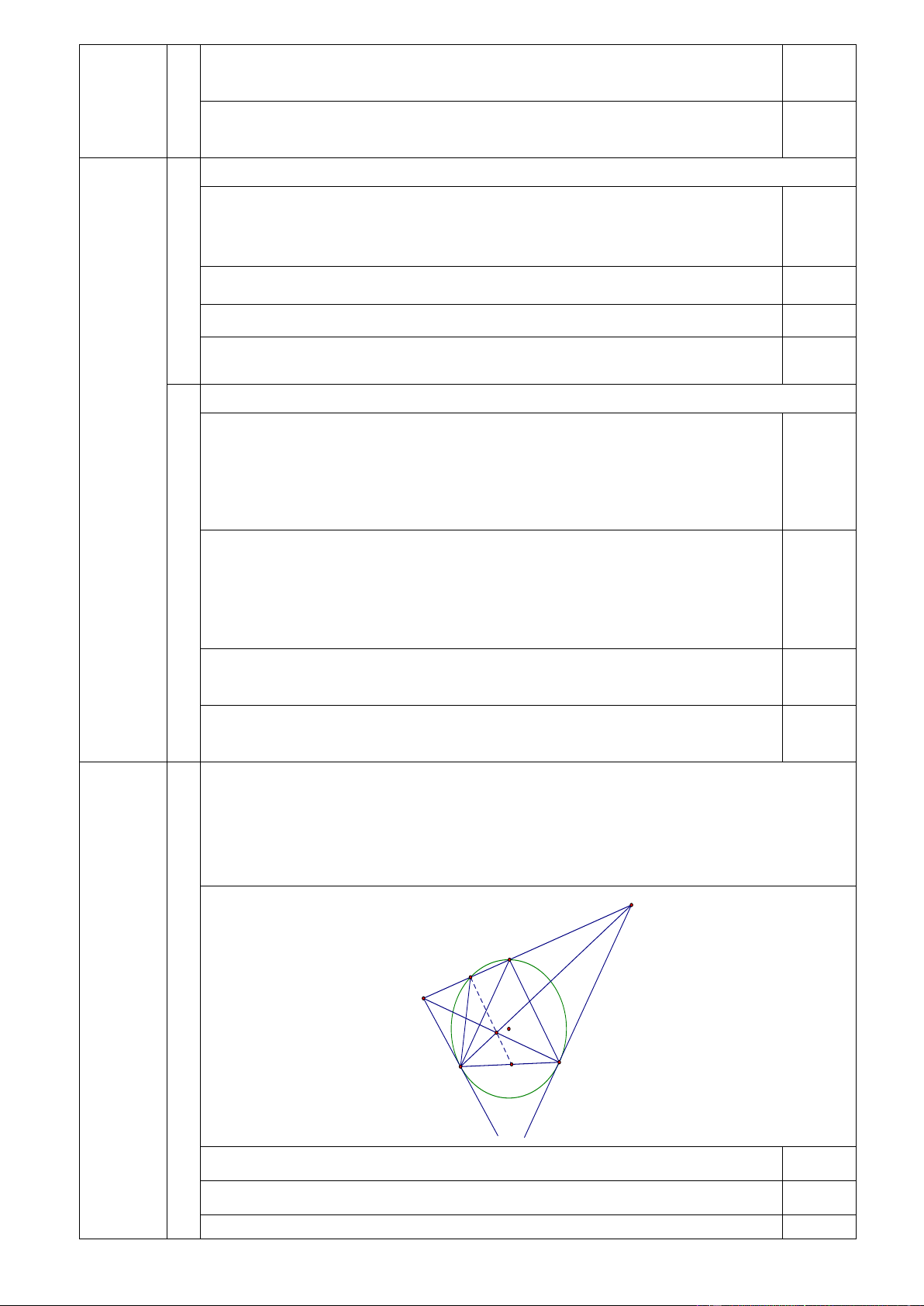
b) Gọi F là giao điểm của MC và BN , H là trung điểm BC . Chứng minh
rằng ba điểm E, F , H thẳng hàng. N A E M O F B C I H
Gọi I là giao điểm của EF và BC . Từ a) suy ra 0,25 MB BC 2 M . B NC  BC   3 2 BC NC Mặt khác 0 0 0
MBC  MBA  ABC  60  60  120 . Tương tự 0 BCN  120
Suy ra MBC  BCN 4 Từ (3) và (4) ta có M
 BC đồng dạng B  CN (c-g-c). Suy ra BMC  NBC Ta có 0 0
BFM  BCF  FBC  BCF  BMC  180  MBC  60 5
Do BEAC nội tiếp nên 0
BEM  BCA  60 6 0,25
Từ (5) và (6) ta có BFM  BEM . Suy ra BMEF nội tiếp
BEF  BMF  NBC  FBI . Do đó I
 BF đồng dạng IEB  (g-g). Suy IB IF 0,25 ra 2 
 IB  IE.IF 7 IE IB
Chứng minh tương tự ta có 2 IC  I . E IF 8 . 0,25
Từ (7) và (8) suy ra IB  IC  I  H . Vậy E, F, H thẳng hàng.
2. Cho đường tròn (O) và hai điểm ,
A B cố định nằm trên đường tròn (O) sao cho · 0
AOB = 120 . Điểm M thay đổi trên cung lớn »
AB của đường tròn (O).
Đường tròn nội tiếp tam giác MAB tiếp xúc với M ,
A MB lần lượt tại E, F .
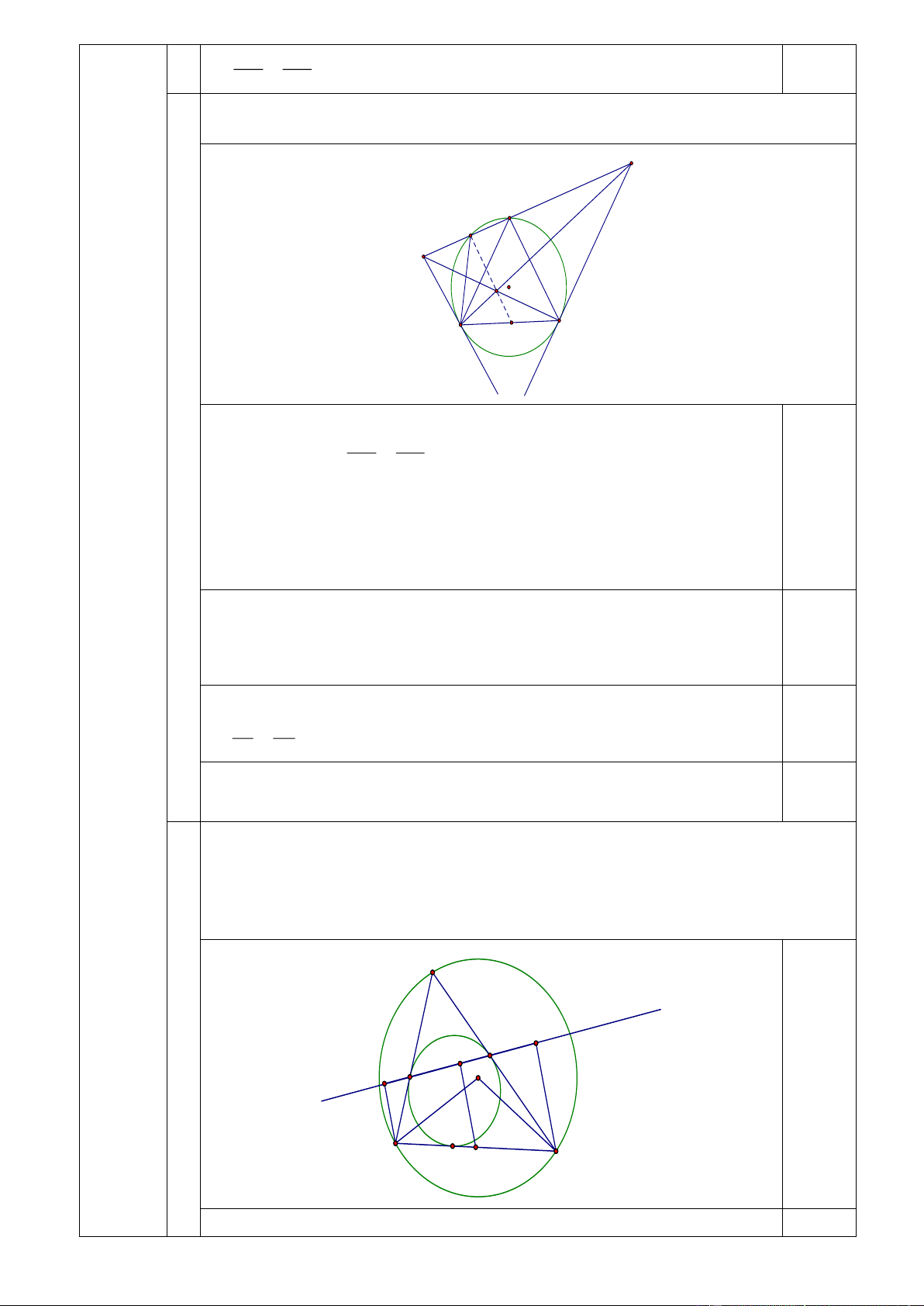
Chứng minh rằng đường thẳng EF luôn tiếp xúc với một đường tròn cố định. M 3 K F J E H O A B D I
Gọi I là trung điểm của AB . Vẽ AH , IJ , BK cùng vuông góc EF . 0,25 Trang 5 Ta có 0 0
AOB  120  AMB  60 , hơn nữa ME  MF nên tam giác MEF đều. 3 3
Tam giác vuông AHE có 0
AH  AE.sin 60  .AE  .AD   1 2 2 0,25 3 3
Tam giác vuông BKF có 0
BK  BF.sin 60  BF  BD 2 2 2
Cộng vế (1) và (2) ta có 3 3 3 0,25 AH  BK  AB  2IJ  AB  IJ  AB không đổi. 2 2 4
Vì điểm I cố định nên EF tiếp xúc với đường tròn cố định tâm I , 3 0,25 bán kính AB . 4
Cho a,b, c là các số không âm và không có hai số nào đồng thời bằng 0 . Chứng minh rằng: 1 1 1 10 + + ³ ( ) * 2 2 2 2 2 2 a + b b + c c + a
(a + b + c)2
Giả sử c  mina, , b  c . Khi đó : 2  c  2 2 2 2
c  a  c  ac  a  c  a  ac  a     2  2  c  0,25 2 2 2 2
c  b  c  bc  b  c  b  bc  b     2  2 2  c   c  2 2
a  b  a   b       2   2  1 1 1 VT ( ) * ³ + + 5 2 2 2 2 æ c ö æ c ö æ c ö æ c ö (1 điể ç ÷ + ç ÷ + ç ÷ + ç ÷ ç ÷ + ç ÷ m) a b b ç ÷ a + ç ÷ çè 2÷ ø çè 2÷ ø çè 2÷ ø çè 2÷ ø Đặ c c 0,25 t x = a + ; y = b +
. Khi đó x > 0, y > 0 và x + y = a + b + c . 2 2 1 1 1 Ta có VT ( ) * ³ + + 2 2 2 2 x + y y x 1 2 1 1 3 4 3 ³ + = + + ³ + 2 2 2 2 2 2 x + y xy x + y 2xy 2xy
x + y + 2xy 2xy 0,25 4 3 4 2 10 10 = + ³ + 3. = = = VP( ) * (x + y)2 2xy (x + y)2 (x + y)2 (x + y)2
(a + b + c)2 ìï c = 0 ìï c = 0 Dấu bằng xảy ra khi ï ï í Û í
. Do vai trò của a,b, c bình đẳng ï x = y ï a = b ïî ïî 0,25 nên dấu “=” của ( )
* xảy ra khi và chỉ khi trong ba số a, b, c có một số
bằng 0 và hai số còn lại bằng nhau.
Lưu ý: Học sinh giải theo cách khác nếu đúng vẫn cho điểm tối đa. Trang 6