Đề thi tuyển sinh 10 THPT năm 2023-2024 toán chuyên Sở GD Thái Bình (có đáp án và lời giải chi tiết)

Tổng hợp Đề thi tuyển sinh 10 THPT năm 2023-2024 toán chuyên Sở GD Thái Bình (có đáp án và lời giải chi tiết) rất hay và bổ ích giúp bạn đạt điểm cao. Các bạn tham khảo và ôn tập để chuẩn bị thật tốt cho kỳ thi tốt nghiệp sắp đến nhé. Mời bạn đọc đón xem.

73 37 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024

Môn: Môn Toán

Thông tin:

4 trang 9 tháng trước

Tác giả:

Profile Minh Thư
Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH THÁI BÌNH
ĐỀ CHÍNH THỨC
ĐỀ THI VÀO LỚP 10 THPT CHUYÊN
NĂM HỌC 2023-2024
MÔN TOÁN CHUYÊN
Thời gian : 150 phút
ĐỀ BÀI
Câu 1:
a) Cho các số thực x,y khác 0, thoả mãn:
3
xy
yx
và
22
10
xy
yx
.
Chứng minh
11
1
xy
b) Cho đa thức bậc 3
Px
thoả mãn khi chia
Px
cho
đều được số dư là 6 và
1 18 P
. Tìm đa thức
Px
c) Cho các số thực không âm a,b,c thoả mãn đồng thời các điều kiện:
abc
= 8;
26; 144 a b c abc
. Tính giá trị biểu thức: P =
111
9 9 9

bc a ca b ab c
Câu 2:
a) Giải phương trình:
2
3 6 4 5 6 1 x x x x
b) Giải hệ phương trình
32
60
2 3 2
x xy y
x y x y xy
Câu 3: Cho tam giác ABC vuông tại A với AB = c, AC = b. Vẽ đường tròn tâm O
1
đường kính AB và
đường tròn tâm O
2
đường kính AC. Gọi H là giao điểm thứ hai của hai đường tròn (O
1
) và (O
2
).
Đường thẳng d thay đổi luôn đi qua A cắt các đường tròn (O
1
) và (O
2
) lần lượt tại các điểm D, E không
trùng với A sao cho A nằm giữa D,E.
a) Chứng minh rằng đường trung trực của đoạn thẳng DE luôn đi qua một điểm cố định khi đường
thẳng (d) thay đổi.
b) Xác định vị trí của đường thẳng (d) để diện tích tứ giác BDEC đạt giá trị lớn nhất. Tìm giá trị lớn
nhất đó theo b,c.
c) Kẻ đường thẳng đi qua trung điểm của đoạn DE và vuông góc với BC tại K. Chứng minh rằng
2 2 2
KB BD KH
Câu 4: Chứng minh rằng nếu p là số nguyên tố lớn hơn 3 thì (7 − p)(7 + p) chia hết cho 24
Câu 5: Cho 3 số thực dương x,y,z thoả mãn
1xy yz zx
. Tìm giá trị lớn nhất của biểu thức:
P =
2 2 2
2 2 2
2
28 28
1 1 1
x y z
x y z
x y z
Trang 2
ĐÁP ÁN
Câu 1: a) Từ giả thiết ta có
22
2 2 3 3
33
3
33
10
10 2 5 , 0


x y xy
x y x y xy x y x y xy x y xy x y
x y xy
xy xy x y x y x y
Ta có
2
22
11
2 5 5 1
xy
x y x y xy xy xy
xy x y
(đpcm)
b) Theo định lý Bezout:
6 1 2 3 P x S x x x x
Do P bậc 3
S x a
. và
1 2 3 4 6 18 1 P a a
Suy ra
32
1 2 3 6 6 11 P x x x x x x x
Thử lại ta thấy đúng.
Vậy
32
6 11 P x x x x
c) Đặt
, , , ,a b c x y z
điều kiện:
, , 0x y z
2 2 2 2 2 2
8; 26; 144 x y z x y z x y z
2
2 2 2
8; 19; 12
2
x y z x y z
x y z xy yz zx xyz
(Do
, , 0x y z
)
Ta có:
1 1 1
9 9 9
P
yz x xz y xy z
Ta có:
9 1 1 1 yz x yz x x y z z y
Tương tự:
9 1 1 ; 9 1 1 xz y x z xy z x y
1 1 1
1 1 1

x y z
x y z
3
1
x y z
xyz x y z xy yz xz
=
11
12 19 8 1
=
11
40
Vậy P =
11
40
Câu 2:
a) Điều kiện:
6
5
x
Từ giả thiết ta có:
2
5 6 4 5 6 x x x x x
2
2
56
5 6 4 .
56

xx
x x x
xx
Vì
6
5
x
nên phương trình tương đương:
2
56
2 3 1 0
56




xx
xx
xx
Do đó x = 2 hoặc x = 3 (thoả mãn điều kiện) hoặc:
3 5 6 xx
(*)
Giải phương trình (*):
2
52
9 5 6 0
93



x x x x
( vô nghiệm vì x ≥
6
5
>
5
9
)
Vậy phương trình có nghiệm x = 2 và x = 3
b)
32
6 0 1
2 3 2 2
x xy y
x y x y xy
Xét (2):
22
2 3 2 2 6 x y x y xy x y
Trang 3
Từ (1):
3 2 2 2 3 2 2 3
2 0 yx 2 0 x xy y x y x xy y
22
20 x y x xy y
Ta để ý (x, y) = (0,0) không là nghiệm của hệ
do đó
2
2 22
2
3
0
4

y
xx yy y x
.
Vậy
2
2 6 6 1 x y y y
Nếu
12 yx
(Thử lại thoả mãn )
Nếu
12 yx
(Thử lại thoả mãn)
Vậy (x,y) = (2,1) và (x,y) = (−2,−1) là nghiệm của hệ.
Câu 3:
a) Gọi M là trung điểm
12
11
;.
22
BC MO AC MO AB
Do D thuộc đường tròn đường kính AB nên tam giác ADB vuông tại D.
12
1
.
2
DO AB MO
Tương tự thì
21
EO MO
Có tam giác ABC vuông tại A (giả thiết).
90
o
ADB EAC
Mà tam giác DAB vuông tại D nên
90
o
ADB DBA
1 2 1 2
22 EAC ABD EAC ABD DO A EO C DO B EO A
Dễ thấy
1 2 1 2 1 2
/ / , / / 90
o
MO AC MO AB MO B MO A MO D MO E
Xét
1
MO D
và
2
EO M
có:
12
MO EO
(cmt)
12
DO M MO E
(cmt)
12
DO MO
(cmt)
1
MO D
2
EO M
(c.g.c)
MD ME
(2 cạnh tương ứng).
M
thuộc trung trực DE. Do đó trung trực DE luôn đi qua M cố định (đpcm).
Trang 4
b) Có
2 2 2 2
11
2 2 2 2 . . .
22
BDEC BDA BAC AEC
S S S S DB DA AB AC EA EC BD DA EA EC bc
2
2 2 2 2
22
1 1 1
2 2 2
11
44
BDEC
AB AC bc b c bc b c
S b c Max b c
Dấu "=" xảy ra
,. DA DB EA EC
d tạo với AB một góc 45°.
c) Ta có điều phải chứng minh:
2 2 2 2 2 2 2 2 2 2 2
KB BD KH IB KI IB ID IH IK IH ID IH ID IE
Do đó tam giác DHE vuông tại H.
Thật vậy, có
90 90
oo
DHB EHC DAB EAC DHE
Do đó tam giác DHE vuông tại H, tức KB
2
= BD
2
+ KH
2
(đpcm).
Câu 4:
Do
p
nguyên tố
3pp
không là bội của 3 và 2
2
1 mod3p
và p
2
1 (mod8)
2
13p
và 8 suy ra
2
1 24p
Vì
3,8 1
nên
22
7 7 49 48 1 24 p p p p
Vậy ta có điều phải chứng minh
Câu 5: Áp dụng bất đẳng thức AM - GM:
22
22
1


x x x
x y x z
x x xy yz zx

xx
x y x z
2


yy
y x y z
y xy yz zx
1
.
4

yx
y z y x
2


zz
z x z y
z xy yz zx
1
.
4

zx
z y z x
2 2 2
2
1 1 1

x y z
x y z
1 + 1 +
1
4
=
9
4
(1)
Và ta có:
2
2
2
22
2
1 1 7
7 7 7 7 2
2 2 2
28 28 x x x zxz yy z
Dấu "=" của các bất đẳng thức (1), (2) xảy ra khi
77x y z
và
1xy yz zx
khi và chỉ khi
15
15
yz
;
7 15
15
x
Từ (1), (2) có
9 19
7
44
P
suy ra MaxP = 7
15
15
yz
;
7 15
15
x
Vậy MaxP =
19
4
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI VÀO LỚP 10 THPT CHUYÊN TỈNH THÁI BÌNH NĂM HỌC 2023-2024 MÔN TOÁN CHUYÊN ĐỀ CHÍNH THỨC
Thời gian : 150 phút ĐỀ BÀI Câu 1: x y 2 2 x y
a) Cho các số thực x,y khác 0, thoả mãn:   3 và   10 . y x y x Chứng minh 1 1   1 x y
b) Cho đa thức bậc 3 P x thoả mãn khi chia P x cho x 1, x  2, x  3 đều được số dư là 6 và P   1  1
 8. Tìm đa thức Px
c) Cho các số thực không âm a,b,c thoả mãn đồng thời các điều kiện: a b c = 8; 1 1 1
a b c  26; abc  144 . Tính giá trị biểu thức: P =   bc a  9 ca b  9 ab c  9 Câu 2: a) Giải phương trình: 2
3x x  6  4x  5x  6   1 3 2 
x xy  6 y  0
b) Giải hệ phương trình   x  
y x  2y  3 xy  2
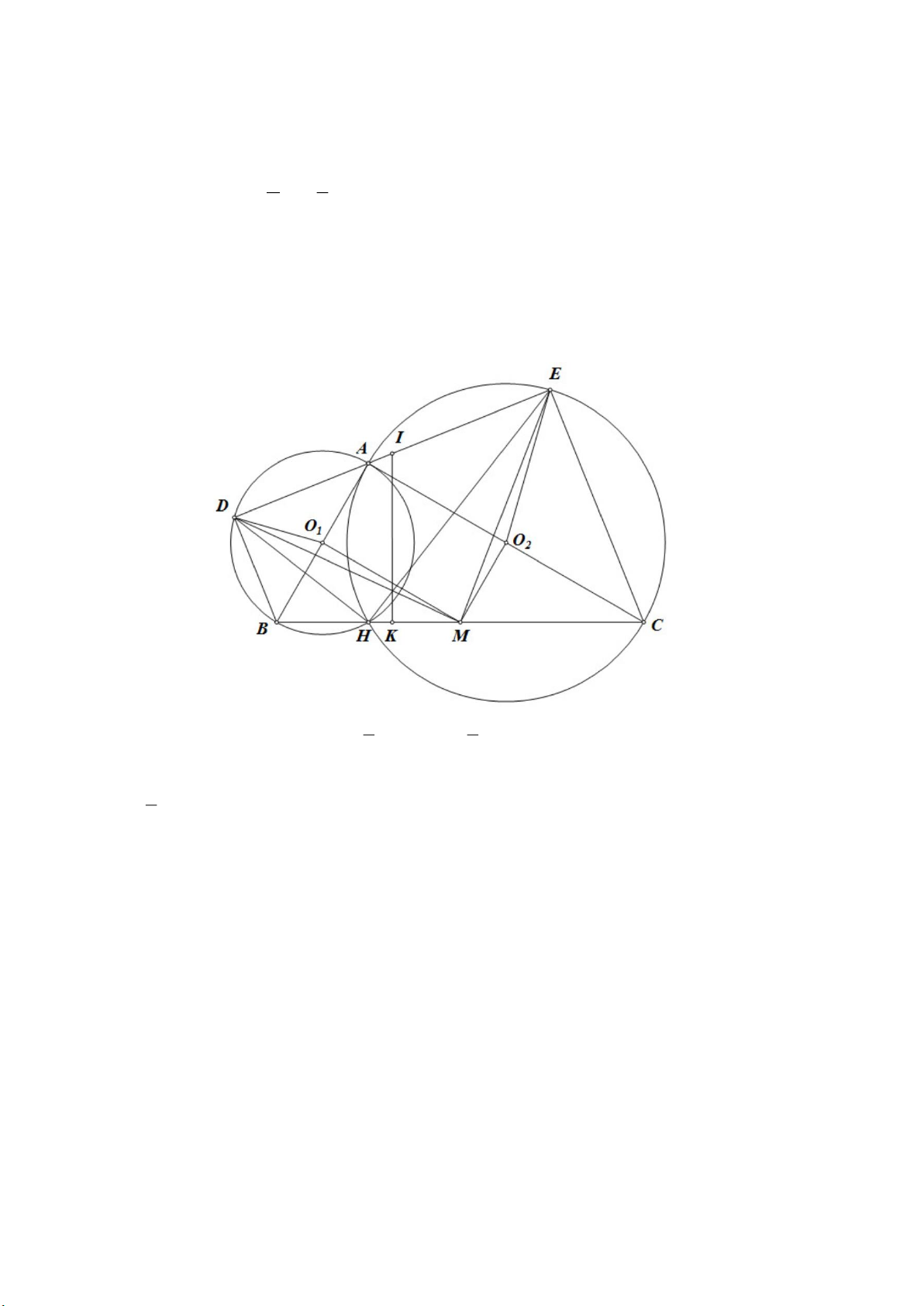
Câu 3: Cho tam giác ABC vuông tại A với AB = c, AC = b. Vẽ đường tròn tâm O1 đường kính AB và
đường tròn tâm O2 đường kính AC. Gọi H là giao điểm thứ hai của hai đường tròn (O1) và (O2).
Đường thẳng d thay đổi luôn đi qua A cắt các đường tròn (O1) và (O2) lần lượt tại các điểm D, E không
trùng với A sao cho A nằm giữa D,E.
a) Chứng minh rằng đường trung trực của đoạn thẳng DE luôn đi qua một điểm cố định khi đường thẳng (d) thay đổi.
b) Xác định vị trí của đường thẳng (d) để diện tích tứ giác BDEC đạt giá trị lớn nhất. Tìm giá trị lớn nhất đó theo b,c.
c) Kẻ đường thẳng đi qua trung điểm của đoạn DE và vuông góc với BC tại K. Chứng minh rằng 2 2 2
KB BD KH
Câu 4: Chứng minh rằng nếu p là số nguyên tố lớn hơn 3 thì (7 − p)(7 + p) chia hết cho 24
Câu 5: Cho 3 số thực dương x,y,z thoả mãn xy yz zx  1. Tìm giá trị lớn nhất của biểu thức: 2x y z P = 2 2 2  
x  28y  28z 2 2 2 1  x y 1 z 1 Trang 1 ĐÁP ÁN
Câu 1: a) Từ giả thiết ta có 2 2
x y  3xy
 x yx y  3xy x y x y xy x y  3xy x y 3 3  2 2   3 3    
x y  10xy
 10xy  2xy x y  x y  5x, y  0 x y 1 1
Ta có  x y2 2 2
x y  2xy  5xy xy  5     1(đpcm) xy x y
b) Theo định lý Bezout: P x  6  S x x  
1  x  2 x  3
Do P bậc 3  S x  a . và P  1  a  2   3   4    6  1  8  a  1
Suy ra P x   x   x   x   3 2 1 2
3  6  x  6x 11x Thử lại ta thấy đúng. Vậy Px 3 2
x  6x 11x
c) Đặt  a, b, c    x, y, z điều kiện: x, y, z  0 2 2 2 2 2 2
x y z  8; x y z  26; x y z  144
x y z2   2 2 2
x y z
x y z  8; xy yz zx
 19; xyz  12 (Do x, y, z  0 ) 2 1 1 1 Ta có: P    yz x  9 xz y  9 xy z  9
Ta có: yz x  9  yz x x y z  1   z   1  y   1
Tương tự: xz y  9  x   1  z  
1 ; xy z  9   x   1  y   1
x  1  y  1  z  1
x y z   3 11 11  = x   1  y   1  z   1
xyz x y z xy yz xz  1 12  19  8  = 1 40 11 Vậy P = 40 Câu 2: 6
a) Điều kiện: x  5 2 x x  Từ giả thiết ta có: 5 6 2
x  5x  6  4x  5x  6  x 2
 x  5x  6  4 . x 5x  6  x 6 
x x   Vì x
nên phương trình tương đương:   x   x   2 5 6 2 3 1   0 5  x  5x  6 
Do đó x = 2 hoặc x = 3 (thoả mãn điều kiện) hoặc: 3x  5x  6 (*)   6 5 Giải phương trình 5 2 (*): 2
9x  5x  6  x x    0   ( vô nghiệm vì x ≥ > )  9  3 5 9
Vậy phương trình có nghiệm x = 2 và x = 3 3 2
x xy  6y  0  1 b) 
x yx  2y  3xy  2 2
Xét (2):  x y x y   xy   2 2 2 3
2  x  2y  6 Trang 2 Từ (1): 3 2
x xy y  2 2 x y  3 2 2 3 2
 0  x xy  yx  2y  0
 x y 2 2 2
x xy y   0
Ta để ý (x, y) = (0,0) không là nghiệm của hệ 2  y  do đó 3 2 2 2
x xy y x   y  0   .  2  4 Vậy 2
x  2 y  6 y  6  y  1 
Nếu y  1  x  2 (Thử lại thoả mãn )
Nếu y  1  x  2 (Thử lại thoả mãn)
Vậy (x,y) = (2,1) và (x,y) = (−2,−1) là nghiệm của hệ. Câu 3: 1 1
a) Gọi M là trung điểm BC MO AC; MO  . AB 1 2 2 2
Do D thuộc đường tròn đường kính AB nên tam giác ADB vuông tại D. 1
DO AB MO . Tương tự thì EO MO 1 2 2 2 1
Có tam giác ABC vuông tại A (giả thiết).   90o ADB EAC
Mà tam giác DAB vuông tại D nên   90o ADB DBA
EAC ABD  2EAC  2ABD DO A EO C DO B EO A 1 2 1 2 Dễ thấy / / , / /    90o MO AC MO AB MO B MO A
MO D MO E 1 2 1 2 1 2
Xét MO D và EO M có: 1 2
MO EO (cmt) 1 2
DO M MO E (cmt) 1 2 DO MO 1 2 (cmt)
 MO D  EO M (c.g.c) 1 2
MD ME (2 cạnh tương ứng).
M thuộc trung trực DE. Do đó trung trực DE luôn đi qua M cố định (đpcm). Trang 3 1 1 b) Có 2S  2S  2S  2SD . B DA A . B AC E . A EC   2 2
BD DA    2 2
EA EC   bc BDEC BDA BAC AEC 2 2 1
  AB AC  1
bc  b c  1
bc  b c2 2 2 2 2 2 2 2 1  S
 b c2 1
Max  b c BDEC 2 4 4
Dấu "=" xảy ra  DA DB, EA EC.  d tạo với AB một góc 45°.
c) Ta có điều phải chứng minh: 2 2 2 2 2 2 2 2 2 2 2
KB BD KH IB KI IB ID IH IK IH ID IH ID IE
Do đó tam giác DHE vuông tại H. Thật vậy, có     90o   90o DHB EHC DAB EAC DHE
Do đó tam giác DHE vuông tại H, tức KB2 = BD2 + KH2 (đpcm). Câu 4:
Do p nguyên tố p  3  p không là bội của 3 và 2 2
p  1mod3 và p2  1 (mod8) 2
p 1 3 và 8 suy ra 2  p 1 24
Vì 3,8  1 nên   p  p 2   p    2 7 7 49 48 p   1 24
Vậy ta có điều phải chứng minh
Câu 5: Áp dụng bất đẳng thức AM - GM: 2x x 2   x x x   2 2 1  x
x xy yz zx
x yx zx y x z y y 1 y x   .  2
y xy yz zx
y x y z 4 y z y x z z 1 z x   .  2
z xy yz zx
z xz y 4 z y z x 2x y z 1 9    1 + 1 + = (1) 2 2 2 1  x y  1 z  1 4 4 1 2 1 2 7 2 Và ta có: 2 2 2
x  28 y  28z
x  7x  x  7z   y z  7  7 2 2 2 2
Dấu "=" của các bất đẳng thức (1), (2) xảy ra khi x  7 y  7z và xy yz zx  1 khi và chỉ khi 15 7 15 y z  ; x  15 15 9 19 15 7 15
Từ (1), (2) có P   7  
suy ra MaxP = 7  y z  ; x  4 4 15 15 19 Vậy MaxP = 4 Trang 4