Đề thi tuyển sinh lớp 10 môn Toán năm 2021 – 2022 sở GD&ĐT Nam Định

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 THPT KHÔNG CHUYÊN NAM ĐỊNH Năm học: 2021 – 2022 Môn: Toán ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút (không kể thời gian phát đề)
Phần I. Trắc nghiệm (2,0 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm.
Câu 1. Điều kiện xác định của biểu thức x  2  3  x là A. 2   x  3. B. 2   x  3. C. 2   x  3. D. 3   x  2 .
Câu 2. Trong các hàm số sau hàm số nào đồng biến trên R? 1 4 A. y  2x  5 . B. y  (1 2)x 1. C. y   x . D. y  x  6 . 3 3 x  3y  1 
Câu 3. Hệ phương trình  có nghiệm  ; x y là 5  x  y  11 A. 2;  1  . B.  1  ;0 . C.  2  ;  1 . D.  1  ; 2 .
Câu 4. Một hình trụ có chiều cao h  5cm , bán kính r  3cm . Thể tích hình trụ đó bằng A. 3 15 cm . B. 3 45cm . C. 3 45 cm . D. 3 75 cm .
Câu 5. Cho tam giác ABC vuông tại A , có đường cao AH  3cm, góc ABC  60 . Độ dài cạnh AC là A. 2cm . B. 3cm . C. 2 3cm . D. 3 2cm.
Câu 6. Biết phương trình 2
2x  7x  4  0 . Có hai nghiệm phân biệt x ; x . Giá trị của biểu thức 1 2
S  2 x  x  x x bằng 1 2  1 2 A. 10 . B. 5 . C. 7  . D. 9  .
Câu 7. Đường thẳng y  2x  3 và đường thẳng 2
y  (m  2)x  m 1song song với nhau khi và chỉ khi: A. m  2  . B. m  0 . C. m  2 . D. m  2  .
Câu 8. Cho tam giác đều ABC có độ dài cạnh 4 3cm , Bán kính đường tròn nội tiếp tam giác ABC bằng: A. 3cm . B. 2 cm . C. 4 cm . D. 6 cm .
Phần II. Tự luận (8,0 điểm) Câu 1. (1,5 điểm)  3  3   3 3 
1) Chứng mính đẳng thức:  2  . 2   1.  3 1   3 1         1 1  x 1
2) Rút gọn biểu thức: A   :   với x  0; x  4.  x  2 x x  2  x  4 x  4 x  2
Vậy với x  0; x  4 : A  . x Câu 2. (1,5 điểm)
1) Tìm tọa độ của tất cả các điểm thuộc parabol 2 y  2
 x có tung độ bằng 8 . 2) Cho phương trình 2 x  m   2 2
1 x  m  2m  0 (với m là tham số). Tìm tất cả các giá trị của m để
phương trình có hai nghiệm phân biệt x ; x (với x  x ) thỏa mãn: x  3 x . 1 2 1 2 1 2  x y  2   3 
Câu 3. (1,0 điểm) Giải hệ phương trình y x   2 2x   3y  1 Câu 4. (3,0 điểm)
1. Mảnh đất hình chữ nhật ABCD có chiều dài AB  6 m , chiều A B
rộng BC  4 m . Người ta trồng hoa trên phần đất là nửa hình tròn
đường kính AD và nửa đường tròn đường kính BC , phần còn lại
của mảnh đất để trồng cỏ. Tính diện tích phần đất trồng cỏ (phần
tô đậm trong hình vẽ bên, kết quả làm tròn đến chữ số thập phân thứ nhất).
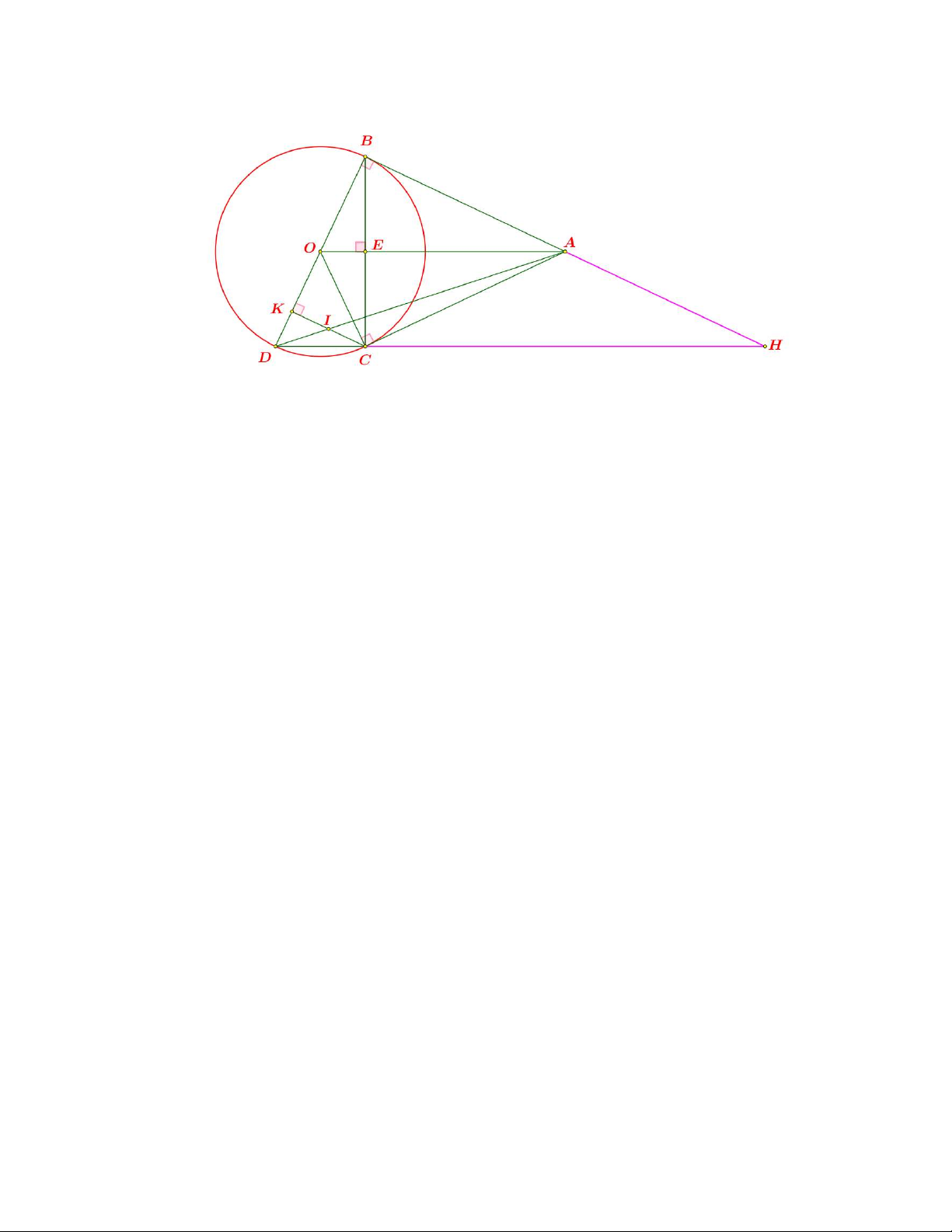
2. Cho O và điểm A nằm bên ngoài đường tròn. Từ A kẻ các D C tiếp tuyến A ,
B AC với đường trònO ( B,C là các tiếp điểm). Kẻ đường kính BD của đường tròn O
a) Chứng minh ABOC là tứ giác nội tiếp đường tròn và  BDC   AOC .
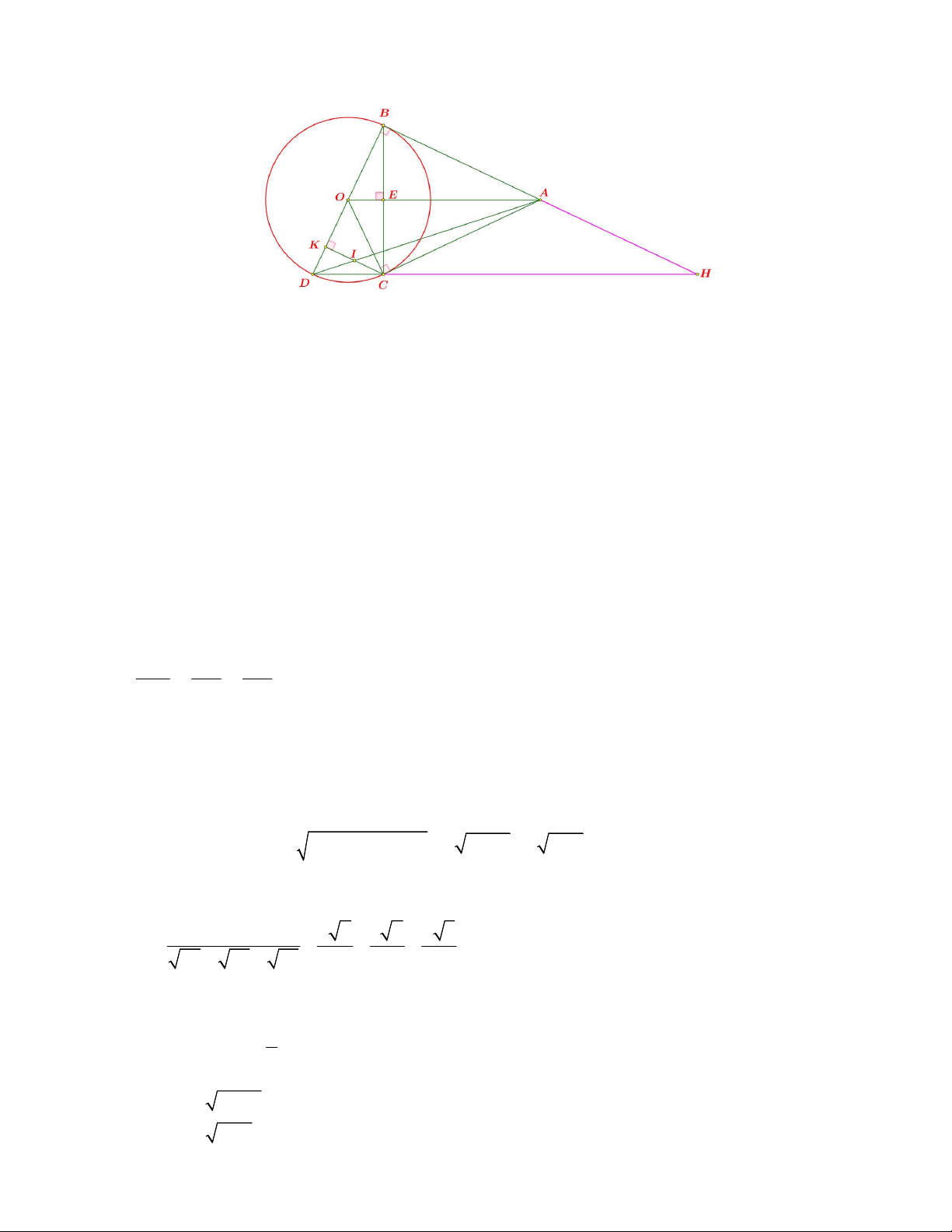
b) Kẻ CK vuông góc với BD tại K . Gọi I là giao điểm của AD và CK . Chứng minh rằng I là trung điểm của CK . Câu 5. (1,0 điểm)
1. Giải phương trình 4x 1 92x   1 x  
1  2 2x 1  2 x 1  0 (1).
2. Cho các số thực dương , a ,
b c thỏa mãn a  b  c  3 . Tìm giá trị nhỏ nhất của biểu thức 2021 b a c b a c P     .
ab  cd  ac 1 b 1 c 1 a
_______________ HẾT _______________
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT I - Trắc nghiệm. Câu 1 2 3 4 5 6 7 8 Đáp án A D A C C B C B II – Tự luận Câu 1. (1,5 điểm)  3  3   3 3 
3) Chứng mính đẳng thức:  2  . 2   1.  3 1   3 1         1 1  x 1
4) Rút gọn biểu thức: A   :   với x  0; x  4.  x  2 x x  2  x  4 x  4 Lời giải.  3  3   3  3  1) Ta có:  2  . 2    3 1   3 1         3  3   1   3  3   1   2 .2    
 2  3.2  3  4 3 1  3 1   3 1     
Vậy đẳng thức được chứng minh. 2) Với x  0; x  4:  1 1  x 1 A   :    x  2 x x  2  x  4 x  4   1 1 x 1      x   x 2 : x  2   x  22  x x   2 2 1 x  2   . x  x  2 . x 1 x x  2
Vậy với x  0; x  4 : A  . x Câu 2. (1,5 điểm)
3) Tìm tọa độ của tất cả các điểm thuộc parabol 2 y  2
 x có tung độ bằng 8 . 4) Cho phương trình 2 x  m   2 2
1 x  m  2m  0 (với m là tham số). Tìm tất cả các giá trị của m để
phương trình có hai nghiệm phân biệt x ; x (với x  x ) thỏa mãn: x  3 x . 1 2 1 2 1 2 Lời giải. 1) Thay y  8
 vào phương trình parabol: 2 y  2  x . Ta có: 2 2 2  x  8   x  4  x  2 
Vậy tọa độ tất cả các điểm thỏa mãn đề bài là: 2;8 và 2; 8 . 2) Phương trình: 2 x  m   2 2 1 x  m  2m  0 (1)
Phương trình (1) là phương trình bậc hai ẩn x có:     m   2     2 m  m 2 2 ' 1 2
 m  2m 1 m  2m  1>0
Phương trình có hai nghiệm phân biệt x ; x với mọi m , mà x  x nên: 1 2 1 2
x  m 11  m x  m 11  m  2 1 2
x ; x thỏa mãn: x  3 x  m  3 m  2 1 2 1 2 m  3m  2 m  3  tm x < x 1 2  3m  6  m        m  3   m  2 3 m  3  m  6 m  tm x < x 1 2   2 3
Vây tất cả các giá trị của m thỏa mãn đề bài là: m  3 và m   . 2 Câu 3. (1,0 điểm)  x y  2   3  Giải hệ phương trình y x   2 2x   3y  1 Lời giải. * Điều kiện: ; x y  0  2 x t    3  1 * Đặt
 t khi đó hệ trở thành  t y 2 2x  3y  1   2 t  1 Giải   1 ta được: 2
t  3t  2  0  t   1 t  2  0  t    2 x * Với t  1 
 1  x  y thế vào 2 ta được: y x 1 2 2x 3x 1 0 x 12x 1 0          1  (thỏa mãn điều kiện) x   2 1   
Vậy suy ra y  1; y  . Do đó hệ phương trình có nghiệm là  x y     1 1 ; 1;1 ; ;   2   2 2  x * Với t  2 
 2  x  2y thế vào 2 ta được: y  y2 2 2 2
 3y 1  0  8y  3y 1  0
Do   23  0 nên phương trình vô nghiệm.   
KL: Vậy hệ phương trình có nghiệm là  x y     1 1 ; 1;1 ; ;     2 2  Câu 4. (3,0 điểm)
1. Mảnh đất hình chữ nhật ABCD có chiều dài AB  6 m , chiều A B
rộng BC  4 m . Người ta trồng hoa trên phần đất là nửa hình tròn
đường kính AD và nửa đường tròn đường kính BC , phần còn lại
của mảnh đất để trồng cỏ. Tính diện tích phần đất trồng cỏ (phần
tô đậm trong hình vẽ bên, kết quả làm tròn đến chữ số thập phân thứ nhất).
2. Cho O và điểm A nằm bên ngoài đường tròn. Từ A kẻ các D C tiếp tuyến A ,
B AC với đường trònO ( B,C là các tiếp điểm). Kẻ đường kính BD của đường tròn O
a) Chứng minh ABOC là tứ giác nội tiếp đường tròn và  BDC   AOC .
b) Kẻ CK vuông góc với BD tại K . Gọi I là giao điểm của AD và CK . Chứng minh rằng I là trung điểm của CK . Lời giải.
1) Diện tích hình chữ nhật ABCD là .   2 6 4 24 m 
Có ABCD là hình chữ nhật  AD  BC  4 m AD 4
Bán kính đường tròn đường kính AD là   2m 2 2 2  2 .
Diện tích nửa đường tròn đường kính AD là  2  2 m  2 BC 4
Bán kính đường tròn đường kính BC là   2m 2 2 2  2 .
Diện tích nửa đường tròn đường kính BC là  2  2 m  2
Diện tích phần đất trồng cỏ là
       ,  2 24 2 2 11 4 m  . 2)
a) Chứng minh ABOC là tứ giác nội tiếp đường tròn và  BDC   AOC . Do A ,
B AC là các tiếp tuyến của đường tròn 0 (gt) AB  OB  
(Tính chất tiếp tuyến) AC  OC Từ đó suy ra  ABO   ACO  90 Xét tứ giác ABOC có:  ABO  
ACO  90  90  180 và hai góc ở vị trí đối nhau
Nên tứ giác ABOC nội tiếp đường tròn. Ta có A ,
B AC là các tiếp tuyến của đường tròn 0 (gt)
Suy ra AB  AC (Tính chất tiếp tuyến) nên A thuộc đường trung trực của BC
Lại có OB  OC  R nên suy ra O cũng thuộc đường trung trực của BC
Từ đó suy ra OA là đường trung trực của BC  OA  BC (1)
Xét O có: BD là đường kính (gt) và C O Suy ra 
DCB  90 (Góc nội tiếp chắn nửa đường tròn)  DC  BC 2
Từ (1) và (2) suy ra OA  CD (Từ vuông góc đến song song)   BDC   AOC
b) Kẻ CK vuông góc với BD tại K . Gọi I là giao điểm của AD và CK . Chứng minh rằng I là trung điểm của CK . Kẻ CD  AB tại H   HCB   BCD  90 Ta có  ACH   ACB  90 và  AHC   ABC  90 Mà  ABC   ACB (do tam giác ABC cân) Từ đó suy ra  ACH   AHC  ACH cân AH  AC
Mà AB  AC nên suy ra AB  AH  AC (3)
Vì HB  CK (Vì cùng vuông góc BD ) CI DI IK   (Định lí Talet) (4) AH DA AB
Từ (3) và (4) suy ra CI  IK
Từ đó suy ra I là trung điểm của CK Câu 5. (1,0 điểm)
1. Giải phương trình 4x 1 92x   1 x  
1  2 2x 1  2 x 1  0 (1).
2. Cho các số thực dương , a ,
b c thỏa mãn a  b  c  3 . Tìm giá trị nhỏ nhất của biểu thức 2021 b a c b a c P     .
ab  cd  ac 1 b 1 c 1 a Lời giải. 1 1. Điều kiện: x  . 2 2
a  2x 1 2x 1 a Đặt 2 2     4x 1  a  2b . 2 b  x 1 x 1  b
Khi đó, phương trình (1) trở thành 2 2 2 2 2
a  2b  3ab  2a  2b  0  a  b  3b  3ab  2a  2b  0
 a  ba  b  3ba  b  2a  b  0  a  ba  b  3b  2  0 a  b  0 a  b    a 2b 2 0     a  2b  2
Với a  b , ta có 2x 1  x 1  2x 1  x 1  x  2 TM . Với a  2b  2 , ta có
2x 1  2 x 1  2  2x 1  2  2 x 1  2x 1 4 2x 1  4  4 x   1  7  4 2 x  TM 2 2 2
 2x 1  4 2x 1  4x  4x 1  32x 16  4x  28x 17  0   74 2 X  KTM  2  7  4 2 
Vậy phương trình có tập nghiệm là S  2  ; .  2   a  b  3  c 
2. Ta có: a  b  c  3  b  c  3 a . a  c  3 b  3  c Vì , a ,
b c dương nên a  b  2 ab  3  c  2 ab  ab  . 2 3  a 3  b Tương tự, ta có: bc  ; ac  . 2 2
9  a  b  c 9  3 Suy ra ab  bc  ca    3. 2 2 Ta có b a b a ab c b c b bc a c a c ac   ;   ;   1 b 2 b 2 1 c 2 c 2 1 a 2 a 2 b a c b a c ab  bc  ca 3 Suy ra     . 1 b 1 c 1 a 2 2 2021 3 4033 Vậy P   
. Dấu “  ” xảy ra khi a  b  c  1 . 3 2 6
__________ THCS.TOANMATH.com __________