SỞ GIÁO DỤC ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 HÀ TĨNH
NĂM HỌC: 2023 – 2024 Môn: TOÁN
Khoá thi ngày: 06/6/2023
Câu 1. (2,0 điểm). Rút gọn các biểu thức sau: a) A  50  3 2  1 1  x b) B   :  
x  0, x 1   x 1 x 1 x 1 Câu 2. (2 điểm)
a)Cho hai đường thẳng d : y  m 1 x  5 (m là tham số) và d : y  3x  2 . Tìm giá trị của 2  1   
m để hai đường thẳng d và d song song với nhau. 2  1 
2x  y  4
b) Giải hệ phương trình  3
 x  2y  1 
Câu 3. (1 điểm). Cho phương trình 2 2
x  2mx  m  m 1  0 (m là tham số). Tìm các giá trị của m  để x x 3 1
phương trình đã cho có hai nghiệm phân biệt x ; x thỏa mãn: 1 2  1 2 2 2
x  x  2 1 x x 3 1 2  1 2 
Câu 4. (1 điểm). Một phòng họp ban đầu có 104 ghế được xếp thành các dãy và số ghế trong mỗi
dãy đều bằng nhau. Có một lần phòng họp phải cắt bớt 2 dãy ghế và mỗi dãy còn lại xếp thêm 1
ghế (số ghế trong mỗi dãy vẫn bằng nhau) để vừa đủ chố ngồi cho 120 đại biểu. Hỏi ban đầu
trong phòng họp có bao nhiêu dãy ghế?
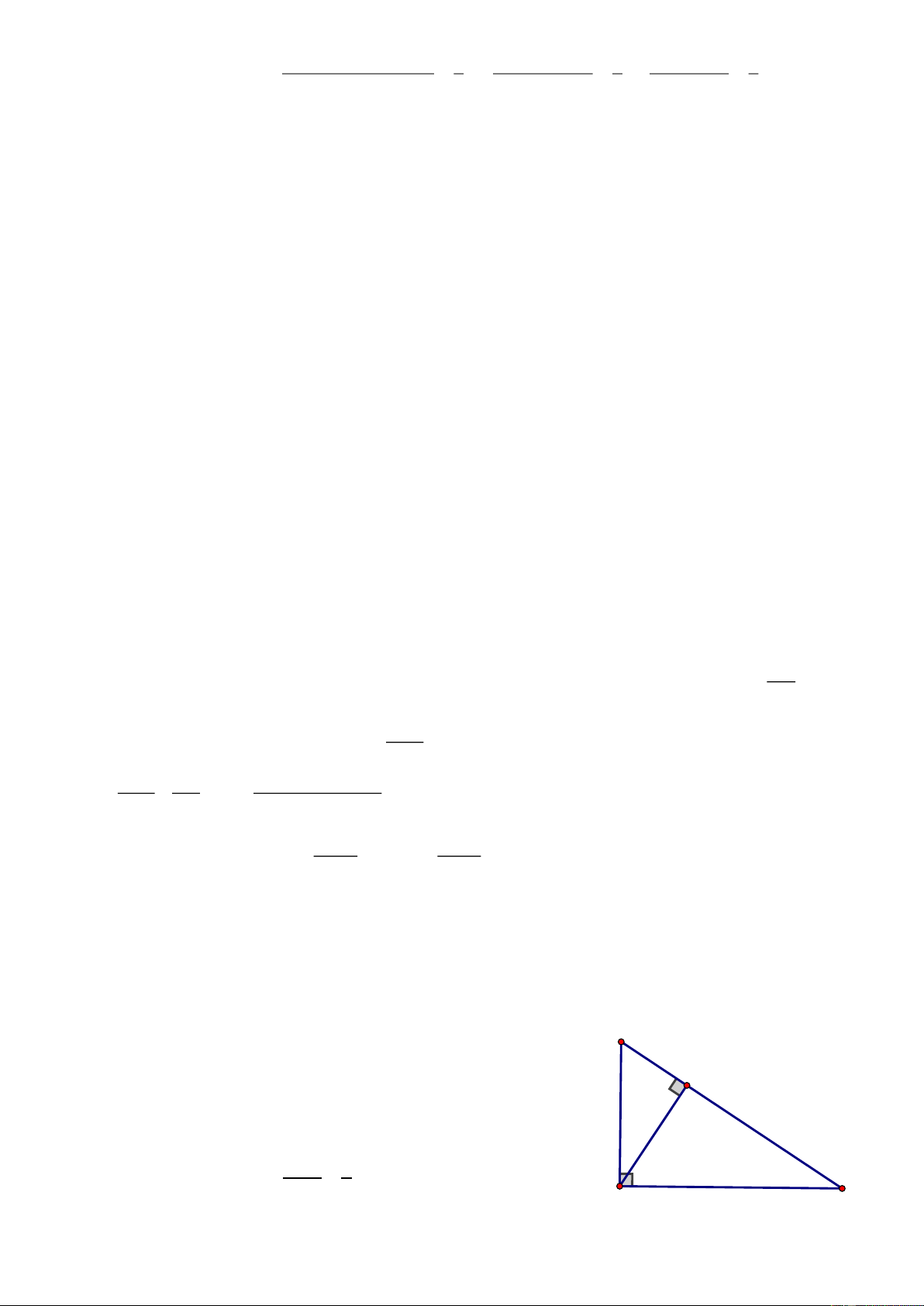
Câu 5. (1 điểm). Cho tam giác ABC vuông tại A, đường cao AH ( (H  BC) . Biết độ dài AC =
5cm và AH = 3cm. Tính độ dài đoạn CH và diện tích tam giác ABC?
Câu 6. (2 điểm) Cho tam giác nhọn ABC. Đường tròn (O) đường kính BC cắt cạnh AB, AC lần
tượt tại E và K (E khác B và K khác C). Gọi H là giao điểm của 2 đường thẳng BK và CE.
a) Chứng minh AEHK là tứ giác nội tiếp.
b) Đường thẳng AH cắt BC tại D và cắt đường tròn (O) tại M (M nằm giữa A và H). Đường
thẳng ED cắt đường tròn (O) tại điểm F (E khác E). Gọi P là giao điểm KF và BC, I là tâm đường
tròn ngoại tiếp tam giác HEM. Chứng minh 2
CK  BC.PC và ba điểm B, I, M thẳng hàng.
Câu 7. (1,0 điểm) Cho a, b, c là ba số thực khác 0. Tìm giá trị nhỏ nhất của biểu thức: 2 2 2 a b c P   
a  b  c2
b  c  a2
c  a  b2 2 2 2 3 3 3 ----------HẾT----------
- Thí sinh không được sử dụng tài liệu.
- Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: ………………………………………………………..Số báo danh: …………………. Trang 1 HƯỚNG DẪN GIẢI
Câu 1. Rút gọn các biểu thức sau: a) 2
A  50  3 2  5 .2  3 2  5 2  3 2  2 2    1 1  x x 1 x 1 x 1 2 x x 1 b) B : =       x  x     x 1
x 1  x 1   x   1  x   . . 2  0, 1  1  x x 1 x  Câu 2. (2 điểm)
a) Cho hai đường thẳng d : y  m 1 x  5 (m là tham số) và d : y  3x  2 . Tìm giá trị 2  1   
của m để hai đường thẳng d và d song song với nhau. 2  1  m 1  3
Để d và d song song với nhau   m  4 2  1  5   2 
b) Giải hệ phương trình
2x  y  4
y  4  2x
y  4  2x y  2        3
 x  2y  1 
2.(2x  y)  3x  2y  8 1 7  x  7 x 1
Câu 3. (1 điểm). Cho phương trình 2 2
x  2mx  m  m 1  0 (m là tham số). Tìm các giá trị của  m để x x 1 1
phương trình đã cho có hai nghiệm phân biệt x ; x thỏa mãn: 1 2  1 2 2 2
x  x  2 1 x x 3 1 2  1 2 
Cách 1: Giả sử phương trình 2 2
x  2mx  m  m 1  0 (1) có hai nghiệm phân biệt x ; x . 1 2
x  x  2m
Theo định lí Vi-ét ta có: 1 2  2
x x  m  m 1  1 2 2 x x  3 1 x x  3 1 m  m  2 1
Mặt khác theo bài ra 1 2 1 2      2 2
x  x  2 1 x x  3 x  x 2 2  2 3 4m  2 3 1 2 1 2 1 2 m  1 2 2 2
 3m  3m  6  4m  2  m  3m  4  0   m  4  Thử lại:
- Với m = 1 thì phương trình (1) trở thành: 2
x  2x 1  0,  '  2  0 suy ra phương trình đã cho có
2 nghiệm phân biệt nên m = 1 thỏa mãn.
-Với m = -4 (1) trở thành: 2
x  8x 19  0,  '  3
  0 suy ra phương trình đã cho vô nghiệm nên m = -4 không thỏa mãn. Vậy m = 1
Cách 2: Để phương trình 2 2
x  2mx  m  m 1  0 (1) có hai nghiệm phân biệt x ; x 1 2 2
    m  2 ' 0 m  m  
1  0  m 1  0  m  1  (*)
x  x  2m
Khi đó Theo định lí Vi-ét ta có: 1 2  2
x x  m  m 1  1 2 Trang 2 2 x x  3 1 x x  3 1 m  m  2 1
Mặt khác theo bài ra 1 2 1 2      2 2
x  x  2 1 x x  3 x  x 2 2  2 3 4m  2 3 1 2 1 2 1 2 m  1 2 2 2
 3m  3m  6  4m  2  m  3m  4  0   m  4 
Đối chiếu điều kiện (*) ta thấy m = 1 thỏa mãn. Vậy m = 1. Bình luận:
- Đối với cách giải 1 học sinh không cần tìm điều kiện của m để phương trình đã cho có 2
nghiệm phân biệt sẽ đơn giản cho HS khi tính biểu thức  hoặc  ' và giải các bất phương trình
  0hoặc '  0 có thể tránh được sai sót khi giải các bất phương trình, thậm chí cả biểu thức 
hoặc  ' theo tham số m.
- Đối với cách giải 2 học sinh đòi hỏi phải nắm vững các phép biến đổi và giải bất phương trình.
Ở trong bài toán trên biểu thức  ' là đa thức bậc 1 nên khá đơn giản nên việc giải các bất phương
trình '  0 đơn giản đối với học sinh (Nếu biểu thức biểu thức  hoặc  ' là các đa thức bậc 2
hoặc cao hơn thì việc giải các bất đẳng thức trên là khó, học sinh thường gặp khó khăn.
Trong quá trình làm bài thì các em có thể linh hoạt theo từng bài toán cụ thể.
Câu 4. (1 điểm). Một phòng họp ban đầu có 104 ghế được xếp thành các dãy và số ghế trong mỗi
dãy đều bằng nhau. Có một lần phòng họp phải cắt bớt 2 dãy ghế và mỗi dãy còn lại xếp thêm 1
ghế (số ghế trong mỗi dãy vẫn bằng nhau) để vừa đủ chố ngồi cho 120 đại biểu. Hỏi ban đầu
trong phòng họp có bao nhiêu dãy ghế? Giải: 104
Gọi x là số dãy ghế ban đầu (dãy, x  2, x  N ), suy ra số nghế của mỗi dãy ban đầu là (ghế) x 120
Theo bài ra, thực tế số ghế mỗi dãy là:
(ghế), vì mỗi dãy xếp thêm 1 nghế nên ta có phương x  2 120 104
120x 104(x  2) trình: 2 2  1 
1  x  2x 16x  208  x 18x  208  0 x  2 x x(x  2) 9 17 9 17 2
 '  81 208  289 17  x   26; x   8 1 2 1 1
Đối chiếu điều kiện ta được x = 26 thỏa mãn.
Vậy ban đầu trong phòng họp có 26 dãy ghế.
Câu 5. (1 điểm). Cho tam giác ABC vuông tại A, đường cao AH ( (H  BC) . Biết độ dài AC =
5cm và AH = 3cm. Tính độ dài đoạn CH và diện tích tam giác ABC? B
Áp dụng định lý Pi-ta-go vào tam giác vuông HAC ta có: H 2 2 2 2 2 2
HC  AC  AH  5  3  16  4  HC  4(c ) m 3cm
Áp dụng hệ thức lượng vào tam giác ABC, đường cao AH ta 2 AH 9 có: 2
AH  BH.HC  HB   (cm) HC 4 A C 5cm Trang 3 9 25
 BC  HC  HB  4   (cm). 4 4 1 1 25 75
Suy ra diện tích tam giác ABC bằng: 2 AH.BC  .3.  (cm ) 2 2 4 8 1
Nhận xét: Để tính diện tích tam giác ABC học sinh có thể sử dụng công thức: S  A . B AC , ABC  2 khi đó tính cạ 1 1 1
nh AB bằng cách áp dụng công thức:   2 2 2 AH AB AC
Câu 6. Cho tam giác nhọn ABC. Đường tròn (O) đường kính BC cắt cạnh AB, AC lần tượt tại E
và K (E khác B và K khác C). Gọi H là giao điểm của 2 đường thẳng BK và CE.
a) Chứng minh AEHK là tứ giác nội tiếp.
b) Đường thẳng AH cắt BC tại D và cắt đường tròn (O) tại M (M nằm giữa A và H). Đường
thẳng ED cắt đường tròn (O) tại điểm F (E khác E). Gọi P là giao điểm KF A
và BC, I là tâm đường tròn ngoại tiếp tam giác HEM. Chứng minh 2
CK  BC.PC và ba điểm B, I, M thẳng hàng. K E Hướng dẫn giải: H
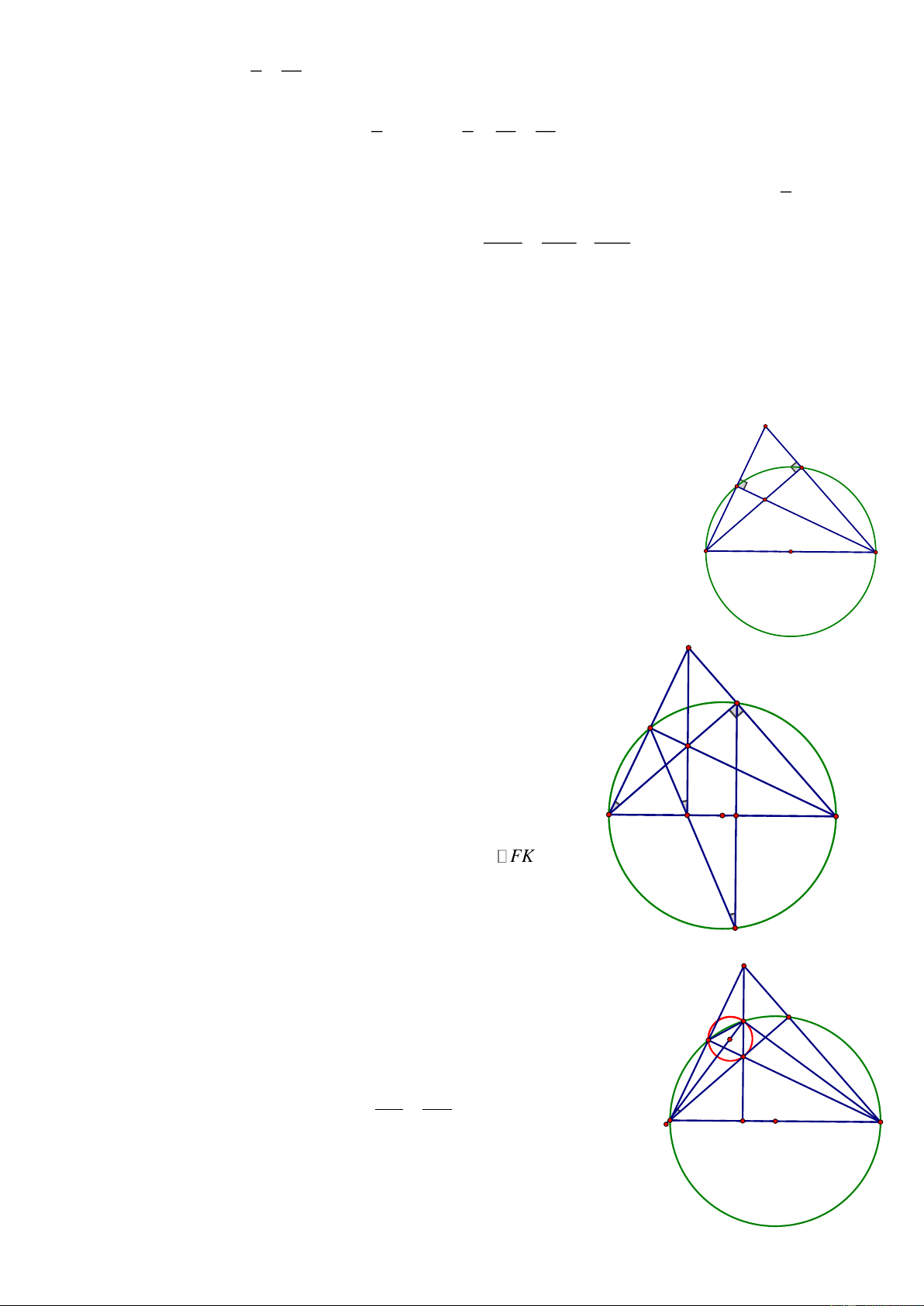
a) Hình 1: Theo bài ra ta có 0
AEH  AKH  90 nên tứ giác AEHK giác nội B C
tiếp đường tròn đường kính AH. Hình 1 b) Hình 2: Chứng minh 2
CK  BC.PC
Theo bài ta có BK  AC;CE  AB , H là giao điểm của BK và A
CE nên H là trực tâm của tam giác ABC nên
AH  BC  HD  BD . Chứng minh tương tự như câu a K E
ta có tứ giác HEBD nội tiếp  1 B 1
D (cùng chắn cung EH của H
đường tròn ngoại tiếp tứ giác HEBD) hay  1 D EBK , mặt khác F  1 1 1
EBK (cùng chắn cung nhỏ EK của đường tròn đường
kính BC hay đường tròn (O). Từ đây suy ra B D P C F   1 1
D mà hai góc này ở vị trí đồng vị DH FK , do Hình 2
DH  BC  FK  BC  KP  BC . Khi đó áp dụng hệ thức lượ 1
ng vào tam giác vuông KBC đường cao KP ta suy ra 2
CK  BC.PC . F A
* Chứng minh: B, I, M thẳng hàng: (Hình 3)
Vì M thuộc nửa đường tròn đường kính BC nên BM  CM (*), mà M K
MD  BC nên áp dụng hệ thức lượng trong tam giác vuông MBC, E I
đường cao MD ta có: 2 CM  C . D CB (1) H CD CH Mặt khác ta có CD  H# CE  B (g.g)    .
CD CB  CH.CE (2) CE CB B D C Từ (1) và (2) ta suy ra: 2
CM  CH.CE nên CM là tiếp tuyến của đường Hình 3
tròn ngoại tiếp tam giác HEM, mà I là tâm của đường tròn ngoại tiếp
tam giác HEM nên IM  MC (**). Từ (*) và (**) ta suy ra ba điểm B, Trang 4 I, M thẳng hàng.
Câu 7. (1,0 điểm) Cho a, b, c là ba số thực khác 0. Tìm giá trị nhỏ nhất của biểu thức: 2 2 2 a b c P   
a  b  c2
b  c  a2
c  a  b2 2 2 2 3 3 3 2 2 4 2 a a a
Cách 1: Ta có: b  c   2 2
2 b  c     2
a  3b  c2 2 a  6  2 2 b  c  4 a  6  2 2 2 2 a b  a c  (dấu = xảy ra khi b =c) 2 4 2 4 Tương tự b b c c ta cũng có:  ;  2
b  3c  a2 4 b  6  2 2 2 2
b c  b a  2
c  3a  b2 4 c  6  2 2 2 2 c a  c b  4 4 4 Do đó a b c P    4 a   2 2 2 2 a b  a c  4 b   2 2 2 2 b c  b a  4 c   2 2 2 2 6 6
6 c a  c b 
Áp dụng BĐT S-vac-xơ (Hệ quả của BĐT Bu-nhi-a-cop-ski) ta có:
a b c a b c 2 2 2 2 4 4 4    4 a   2 2 2 2 a b  a c  4 b   2 2 2 2 b c  b a  4 c   2 2 2 2
c a  c b   2 2 2
a  b  c 2   2 2 2 2 2 2 6 6 6
10 a b  b c  c a  1
Mà a b  b c  c a  a  b  c 2 2 2 2 2 2 2 2 2 2 suy ra: 3
a b c 2
a b c 2 2 2 2 2 2 2 3 3     P  2 2 2
a  b  c 2   2 2 2 2 2 2
a b  b c  c a   10 2 2 2
a  b  c 2   2 2 2
a  b  c 2 13 13 10 3 3
Vậy P đạt giá trị nhỏ nhất bằng
khi a  b  c  0 . 13 2
Cách 2. Ta có: b  c   2 2
2 b  c   6. 1 1  2 2 2 2 2 2 2
a  b  c a a a a        2
a  3b  c2 2 a  6 2 2 b  c  2
a  3b  c2 2 5 a  6 2 2
b  c  5 5. 2 2 2
a  6b  6c  (dấu = xảy ra khi b =c) 6. 6. 1  2 2 2 2
a  b  c c  1  2 2 2 2
a  b  c b  Tương tự:   ;   2 2
b  3c  a2 5 5. 2 2 2
b  6c  6a  2
c  3a  b 5 5. 2 2 2
c  6a  6b  Do đó suy ta 3 6   P    1 1 1 2 2 2
a  b  c      2 2 2 2 2 2 2 2 2 5 5
 a  6b  6c
b  6c  6a
c  6a  6b  6    9  6 9 54 2 2 2
a  b  c    2 2 2
a  b  c    2 2 2 2 2 2 2 2 2  5
 a  6b  6c  b  6c  6a  c  6a  6b  5 13 2 2 2
a  b  c  65 54 3 3 3 P   
. Vậy P đạt giá trị nhỏ nhất bằng
khi a  b  c  0 . 65 5 13 13
---------------------------------@Hết@--------------------------------- Trang 5 Trang 6