Đề thi tuyển sinh lớp 10 năm 2023-2024 môn toán Sở GD và ĐT Nam Định (có đáp án và lời giải chi tiết)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH VÀO LỚP 10 NAM ĐỊNH
THPT KHÔNG CHUYÊN NĂM HỌC 2023 – 2024 MÔN: TOÁN ĐỀ CHÍ NH THỨC.
(Thời gian làm bài: 120 phút)
Đề thi gồm 02 trang.
Phần I: Trắc nghiệm (2,0 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm. 5
Câu 1: Điều kiện xác định của biểu thức là x  2023 1
A. x  2023. B. x  2023. C. x  2023. D. x  2023.
Câu 2: Hàm số nào sau đây đồng biến với mọi x  ? A. y     2 1
5 x . B. y  x  3. C. y  2  7  x  2. D. 2 y  x .
Câu 3: Phương trình 2
2x  x 1  0 có hai nghiệm x , x trong đó x  x . Giá trị 2x  x bằng 1 2 1 2 1 2 A. 0. B. 1  ,5. C. 2.  D. 2.
Câu 4: Với giá trị nào của m thì đường thẳng y  m  
1 x  2 đi qua điểm ( A 1;1) ? A. m  0. B. m  1. C. m  2. D. m  2.  x  y 
Câu 5: Số nghiệm của hệ phương trình 2 5  là
x  3y  2 A. 2 . B. 0. C. 1. D. vô số. Câu 6: Cho ABC  vuông tại ,
A biết AC  6, BC  10. Khi đó tan B có giá trị bằng 3 3 4 5 A. . B. . C. . D. . 4 5 3 3
Câu 7: Một hình nón có bán kính đáy bằng 4 ,
cm chiều cao bằng 6 .
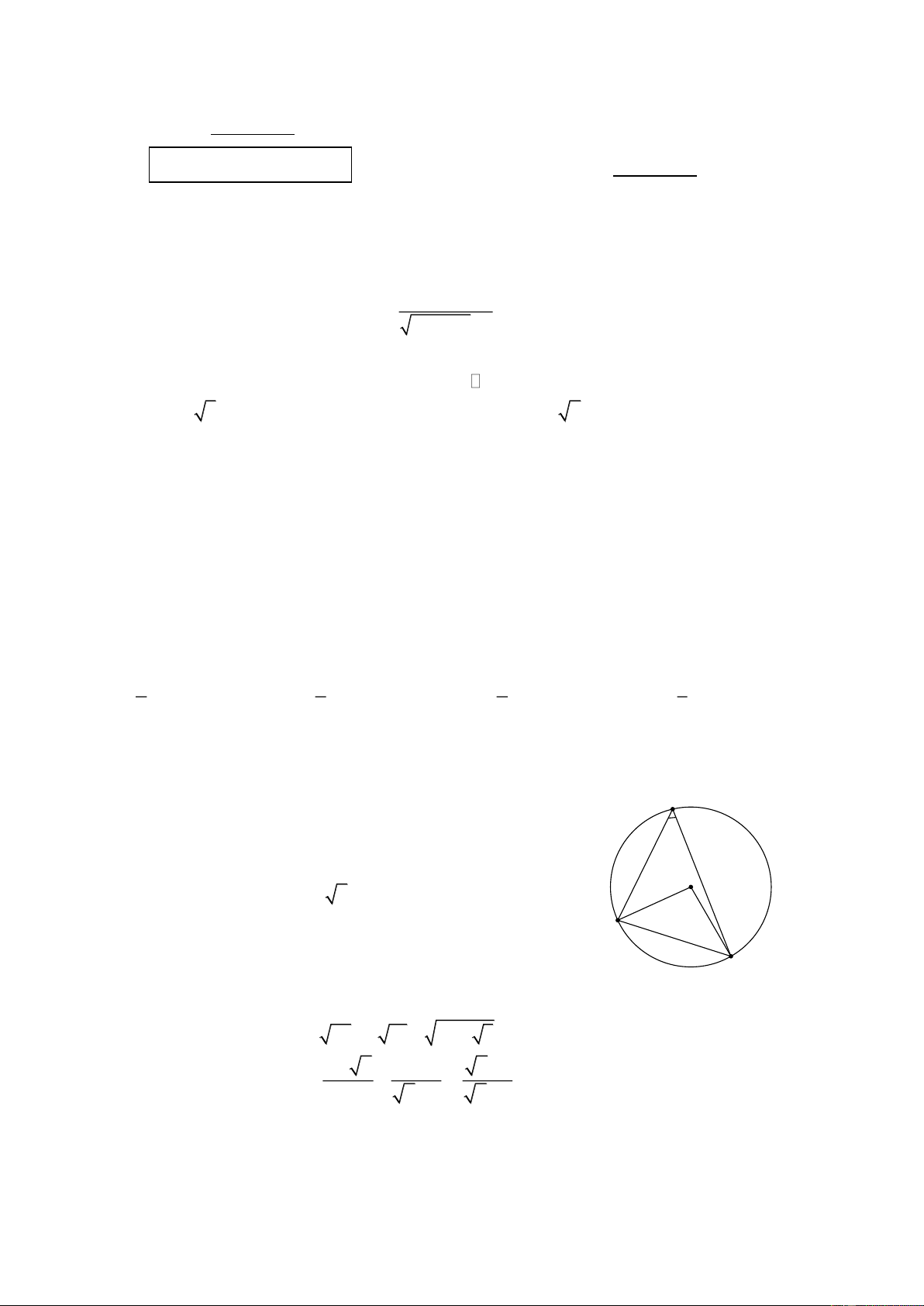
cm Thể tích của hình nón đã cho là A. 3 96 cm . B. 3 32 cm . C. 3 30 cm . D. 3 36 cm . Câu 8: Cho ABC  có 45o BAC 
, nội tiếp trong đường tròn A
tâm O bán kính 2 .
cm Diện tích tam giác OBC bằng o 45 A. 2 1cm . B. 2 4 cm . O C. 2 2 cm . D. 2 2 2 cm . B
Phần II: Tự luận (8,0 điểm) C
Câu 1 (1,5 điểm).
a) Chứng minh đẳng thức 27  2 12  4  2 3  1  .     b) Rút gọn biểu thức 9 x 2 x 1 A     :  
với x  0 và x  9. x  9 x  3 x  3  
Câu 2 (1,5 điểm).
a) Tìm toạ độ giao điểm của đồ thị hai hàm số 2
y  x và y  2  x  3. b) Cho phương trình 2
x  2m  
1 x  6m  4  0 (với m là tham số). Tìm tất cả các giá trị của m
để phương trình có hai nghiệm x , x thoả mãn 2 2
x  x  3x x x  x . 1 2 1 2  2 1  1 2
x  3y  4 
Câu 3 (1,0 điểm). Giải hệ phương trình  1 1   1. x 4 y
Câu 4 (3,0 điểm).
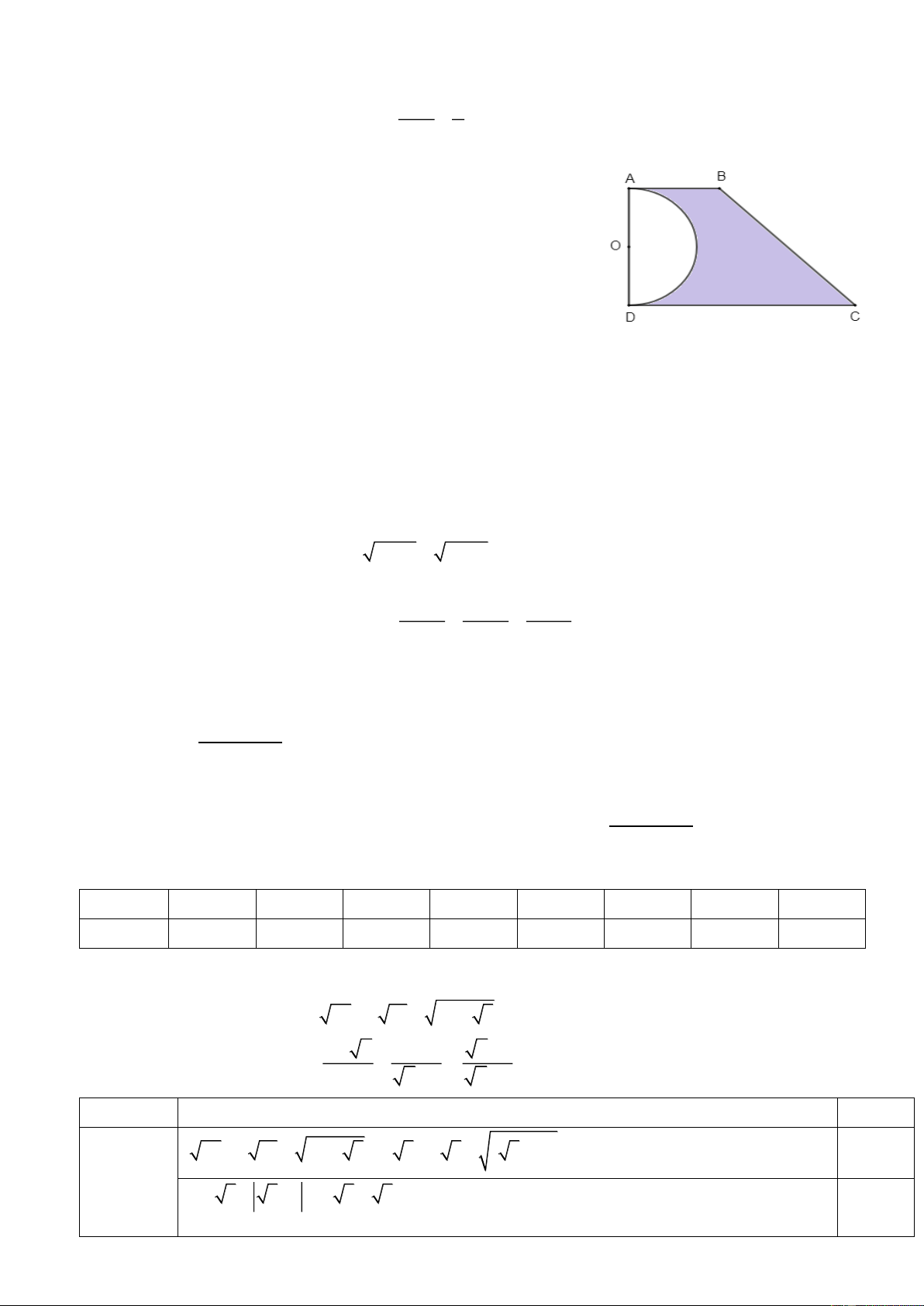
1) Một mảnh vườn hình thang ABCD có   90o BAD ADC , AB  3 , m AD  5 , m DC  7 .
m Người ta trồng hoa trên phần đất là
nửa hình tròn tâm O đường kính AD, phần còn lại của mảnh vườn
để trồng cỏ (phần tô đậm trong hình vẽ bên). Tính diện tích phần
đất trồng cỏ (kết quả làm tròn đến chữ số thập phân thứ hai, lấy   3,14 ).
2) Cho tam giác ABC nhọn  AB  AC nội tiếp (O). Hai đường cao AD và BE cắt nhau tại H.
Gọi M là trung điểm của AH , đường thẳng đi qua M vuông góc với BM cắt AC tại N. Gọi K là
giao điểm thứ hai của AH với đường tròn tâm . O
a) Chứng minh bốn điểm B, M , E, N cùng thuộc một đường tròn và MBN  KAC.
b) Kéo dài KN cắt đường tròn O tại T. Chứng minh tam giác BHK cân và ba điểm B,O,T thẳng hàng.
Câu 5. (1,0 điểm). a) Giải phương trình 2
x  4x  2 1 3x  2x 1.
b) Cho x, y, z là các số thực dương thỏa mãn x  y  z  1. Tìm giá trị nhỏ nhất của biểu thức x  yz y  zx z  xy P    . y  z z  x x  y ------- HẾT -------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM ĐỀ THI TUYỂN SINH LỚP 10 NAM ĐỊNH
THPT KHÔNG CHUYÊN NĂM HỌC 2023-2024 Môn: Toán
Phần I: Trắc nghiệm (2,0 điểm)
Mỗi đáp án đúng được 0,25 điểm. Câu 1 2 3 4 5 6 7 8 Đáp án A B A D C A B C
Phần II: Tự luận (8,0 điểm)
Câu 1. (1,5 điểm)
a) Chứng minh đẳng thức 27  2 12  4  2 3  1  .     b) Rút gọn biểu thức 9 x 2 x 1 A     :  
với x  0 và x  9. x  9 x  3 x  3   Ý Nội dung Điểm a         2 0,25 27 2 12 4 2 3 3 3 4 3 3 1 (0,5 điểm)
  3  3 1   3  3 1  1. 0,25
Vậy 27  2 12  4  2 3  1  . b   9  x 2 x 1   (1,0
Với x  0 và x  9 ta có A  0,25    
x  3 x  3 : x  3  x  3 điểm) 
9  x  2  x  3 x 1 x  3 x 1    0,25
x  3 x  3 : x 
 x 3 x 3 : 3 x  3 x  3 x   3 0,25 
x  3 x  3 . x  1  1 . Vậy 1 A 
với x  0 và x  9. 0,25 x  1 x 1
Câu 2. (1,5 điểm)
a) Tìm toạ độ giao điểm của đồ thị hai hàm số 2
y  x và y  2  x  3. b) Cho phương trình 2
x  2(m 1)x  6m  4  0 (với m là tham số). Tìm tất cả các giá trị của m
để phương trình có hai nghiệm x , x thoả mãn 2 2
x  x  3x x x  x . 1 2 1 2  2 1  1 2 Ý Nội dung Điểm a
Hoành độ giao điểm của đồ thị hai hàm số 2
y  x và y  2
 x  3 là nghiệm (0,5 x  1 0,25 của phương trình 2     điểm) x 2x 3 0  x  3 
Vậy toạ độ các điểm cần tìm là 1  ;1 và  3  ;9. 0,25 b
Ta có   m  2 ' 2 1 0  . m (1,0 0,25 điểm)
Do đó phương trình đã cho luôn có hai nghiệm phân biệt x , x với . m  1 2     Theo hệ thức Vi x x 2(m 1) -et ta có 1 2  0,25
x x  6m  4.  1 2 Ta có 2 2
x  x  3x x x  x  x  x
x  x  3x x  0 1 2 1 2  2 1   1 2  1 2 1 2 
 x  x  3x x  0 (do x , x phân biệt) 1 2 1 2 1 2 0,25   1
m     m   1 2 1 3 6 4  0  m  . Vậy m  . 2 2 0,25
x  3y  4  1 
Câu 3. (1,0 điểm) Giải hệ phương trình  1 1  1  2  x  4 y Nội dung Điểm
ĐKXĐ: x  4; y  0 0,25 PT   1  x  4  3  y 0,25 Thay x  4  3
 y vào PT2 ta có 1 1 2
  1  y   x  2. 0,25 3  y y 3
Đối chiếu với ĐKXĐ ta có    x y  2 ;  2;   là nghiệm của hệ. 0,25  3 
Câu 4. (3,0 điểm)
1) Một mảnh vườn hình thang ABCD có   90o BAD ADC , AB  3 , m AD  5 , m DC  7 . m Người
ta trồng hoa trên phần đất là nửa hình tròn tâm O
đường kính AD, phần còn lại của mảnh vườn để
trồng cỏ (phần tô đậm trong hình vẽ bên). Tính diện
tích phần đất trồng cỏ (kết quả làm tròn đến chữ số
thập phân thứ hai, lấy   3,14 ).
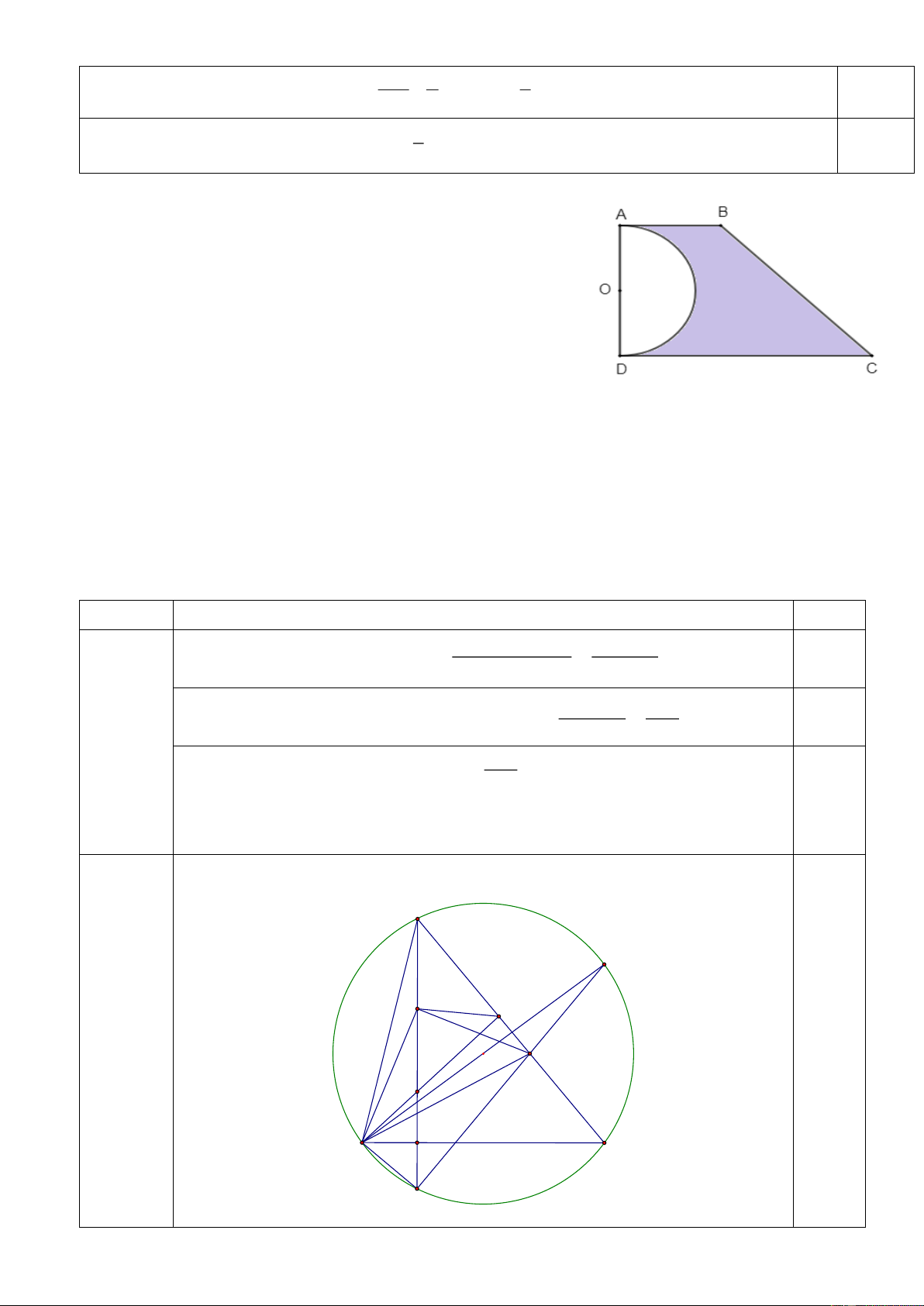
2) Cho tam giác ABC nhọn  AB  AC nội tiếp (O). Hai đường cao AD và BE cắt nhau tại H. Gọi
M là trung điểm của AH , đường thẳng đi qua M vuông góc với BM cắt AC tại N. Gọi K là giao
điểm thứ hai của AH với đường tròn tâm . O
a) Chứng minh rằng bốn điểm B, M , E, N cùng thuộc một đường tròn và MBN  KAC.
b) Kéo dài KN cắt đường tròn O tại T. Chứng minh rằng tam giác BHK cân và ba điểm
B, O,T thẳng hàng. Ý Nội dung Điểm 1
 AB  DC.AD 3 7 Diện tích hình thang .5 ABCD là 2   25m . (1,0 2 2 0,25 điểm) .2,52
Diện tích nửa hình tròn đường kính 25 AD là 2  m . 2 8 0,25
Diện tích phần đất trồng cỏ là 25 2 25   15,19 m . 8 0,5
Chú ý: Nếu học sinh không làm tròn thì trừ 0,25 điểm bước này. 2a (1,0 A điểm) T M E N O H D B C K Ta có 0
BMN  90  M thuộc đường tròn đường kính BN. 0,25 Ta có 0
BEN  90  E thuộc đường tròn đường kính BN.
Do đó bốn điểm B, M , E, N cùng thuộc đường tròn đường kính BN. 0,25
Chứng minh được MBN  MEA. 0,25 Xét AEH 
vuông tại E, có EM là đường trung tuyến
 EM  AM  A
 ME cân tại M  MEA  MAE  MBN  KAC. 0,25 2b
Xét (O) có KBC  KAC mà KAC  EBC (cùng phụ với ACB ) 0,25 (1,0
 KBC  EBC điểm)
 BC là tia phân giác của góc KBH. Lại có BC  HK  B  HK cân tại 0,25 . B
 BKH  BHK. Ta có BHK  MHE  MEH  MNB  BKM  BNM.
Do đó tứ giác BMNK nội tiếp. 0,25 0 0
 BMN  BKN 180  BKN  BKT  90  K thuộc đường tròn đường kính BT. Mà ,
B K,T O  BT là đường kính của (O)  B,O,T thẳng 0,25 hàng.
Câu 5. (1,0 điểm) a) Giải phương trình 2
x  4x  2 1 3x  2x 1.
b) Cho x, y, z là các số thực dương thỏa mãn x  y  z  1. Tìm giá trị nhỏ nhất của biểu thức x  yz y  zx z  xy P    . y  z z  x x  y Ý Nội dung Điểm a  1 x       (0,5 ĐKXĐ: 1 3x 0  3 1     x  . điểm) 2x 1  0 1 2 x   2 Ta có: 2
x  4x  2 1 3x  2x 1 0,25 2
 x  4x  5  2 1 3x  2  2x 1  1     
 x  x   21 3x 4 2x 1 1 1 5   1 3x  2 2x 1 1   
 x  x   6 x  1 2 x  1 1 5   1 3x  2 2x 1 1     x   6 2 1 x  5    0    1 3x  2 2x 1 1  x 1 (tm)   6 2 x  5    1 3x  2 2x 1 1 Xét phương trình 6 2 x  5   * 1 3x  2 2x 1 1 1 11 Do x   6 2 6 2 
   5 và x  5   5 2 1 3x  2 2x 1 1 2 1 2 nên phương trình   * vô nghiệm. 0,25
Vậy phương trình đã cho có nghiệm duy nhất x 1. b
Từ giả thiết x  y  z 1 x  yz  x(x  y  z)  yz  (x  y)(x  z). (0,5
Tương tự y  zx  (y  z)(y  x); z  xy  (z  x)(z  y). 0,25 điểm) Do đó
(x  y)(x  z)
( y  z)( y  x)
(z  x)(z  y) P    . y  z z  x x  y
Đặt x  y  a, y  z  b, z  x  c  a,b,c  0 và a bc  2. 1  ab ac   bc ba   ca cb  P             2  c b   a c   b a  1  ab ac bc ba ca cb   2 .  2 .  2 .
  a  b  c  2.   2 c b a c b a   0,25 Dấu "  " xảy ra khi 2
a  b  c  . 3
Vậy giá trị lớn nhất của biểu thức 1
P bằng 2 khi x  y  z  . 3
Chú ý: - Nếu thí sinh làm đúng mà cách giải khác với đáp án và phù hợp với kiến thức của chương
trình THCS (theo giới hạn quy định của Sở GDĐT) thì tổ chấm thống nhất cho điểm thành phần đảm
bảo tổng điểm như hướng dẫn quy định.
- Tổng điểm toàn bài không làm tròn.
----------HẾT---------
Họ và tên học sinh:……………………………. Họ tên, chữ ký của GT 1:…………………………….
Số báo danh:………….……………………….. Họ tên, chữ ký của GT 2:…………………………….