Đề thi tuyển sinh lớp 10 năm học 2017 – 2018 môn Toán trường THPT chuyên Quốc học – TT Huế

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUỐC HỌC THỪA THIÊN HUẾ NĂM HỌC 2017-2018 Khóa ngày : 02/6/2017 ĐỀ CHÍNH THỨC
Môn thi: TOÁN (CHUYÊN TOÁN)
Thời gian làm bài: 120 phút (không kể thời gian giao đề) Câu 1: (1,5 điểm) 1 9  x x  1
a) Cho các biểu thức P(x)   , Q(x) 
với x  0. Tìm số nguyên x nhỏ nhất x x  3 x x P(x) 1 thỏa mãn  . Q(x) 2 4 3 2
2x  21x  55x  32x  4012
b) Tính giá trị của biểu thức F 
khi x  5  3 (không sử dụng 2 x  10x  20 máy tính cầm tay). Câu 2: (2,0 điểm) 2
a) Trong mặt phẳng tọa độ Oxy, cho parabol (P) : y  x , đường thẳng d có hệ số góc k và đi qua
điểm M (0;1). Chứng minh rằng với mọi giá trị của k, (d) luôn cắt (P) tại hai điểm phân biệt A và
B có hoành độ x ,x x  x  2. 1 2 thỏa điều kiện 1 2  3 3 x   y  9 
b) Giải hệ phương trình  . 2 2 x
  2y  x  4y 
Câu 3: (1,5 điểm) Cho phương trình 2 2 2
x  2(m  1) x  1  m  m  2  0 (1) (x là ẩn số).
a) Giải phương trình (1) khi m  0.
b) Tìm tất cả các giá trị của m để phương trình (1) có bốn nghiệm phân biệt.
Câu 4: (3,0 điểm) Cho đường tròn (O) có tâm O và hai điểm C, D trên (O) sao cho ba điểm C,O,D
không thẳng hàng. Gọi Ct là tia đối của tia C ,
D M là điểm tùy ý trên Ct, M khác C. Qua M kẻ các tiếp  tuyến ,
MA MB với đường tròn (O) (A và B là các tiếp điểm, B thuộc cung nhỏ CD). Gọi I là trung
điểm của CD, H là giao điểm của đường thẳng MO và đường thẳng AB.
a) Chứng minh tứ giác MAIB nội tiếp.
b) Chứng minh đường thẳng AB luôn đi qua một điểm cố định khi M di động trên tia Ct. 2 MD HA c) Chứng minh  . 2 MC HC Câu 5: (2,0 điểm) a) Cho a, ,
b c là các số dương thay đổi và thỏa mãn điều kiện ab  bc  ac  1. Tìm giá trị nhỏ 2 2 2 a b c
nhất của biểu thức E    . a  b b  c c  a
b) Tìm tất cả các số nguyên dương n sao cho 2 3n n 
là một số chính phương. Hết
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
ĐÁP ÁN KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUỐC HỌC NĂM HỌC 2017 – 2018
Khóa ngày 02 tháng 6 năm 2017 Môn thi: TOÁN
Thời gian làm bài: 120 phút, không kể thời gian phát đề NHÓM GIẢI ĐỀ:
1. ThS. TRẦN NGỌC ĐỨC TOÀN. 2. THẦY NGUYỄN VĂN VŨ.
3. THẦY HOÀNG ĐỨC VƯƠNG.
Câu 1. Với x  0 ta có:  3 x3 1 9 1  x x
 1 3 x 1 3 x x P(x)        x  3 x x 3  x  x x x x x P(x) 1  3 x  x x  1 1  3 x  x x 1  3 x  x   :  .  Q(x) x x x x  x x  x P(x) 1 1  3 x  x 1   
 2  6 x  2x  x  x  3x  5 x  2  0 Q(x) 2  2 x x
  x  23 x  
1  0  x  2  0  x  4.
Do đó x nguyên dương nhỏ nhất và x thỏa mãn ycbt là x  4.
b) Thực hiện phép chia đa thức cho đa thức ta có: 4 3 2
2x  21x  55x  32x  4012 2 38x  4112 F 
 2x  x  5  2 2 x  10x  20 x  10x  20
Thay x  5  3 vào F ta được:   2    385  3 4112 2 5 3 5
3  5  5 32105 320     385  3 4112 2 28
10 3  5  3  5  2810 35010 3 20 3922  38 3  56  19 3 
 56  19 3  1961  19 3  2017 . 2 Câu 2.
a) Đường thẳng (d) có hệ số góc k nên có phương trình (d) : y  kx  b
Vì (d) qua M (0;1) nên ta có 1  0k  b  b  1  (d) : y  kx  1
Phương trình hoành độ giao điểm của (P) và (d ) : 2 2
x  kx  1  x  kx  1  0 (*)
NHÓM GIẢI ĐÊ: ThS. Trần Ngọc Đức Toàn – Thầy Nguyễn Văn Vũ – Thầy Hoàng Đức Vương
Vì a,c trái dấu nên (*) luôn có hai nghiệm phân biệt. Nói cách khác, (d) luôn cắt (P) tại hai điểm phân
biệt A và B có hoành độ x , x 1 2 .
Theo định lí Viet, ta có S  x  x  k,P  x x  1  1 2 1 2
Khi đó: x  x
 2  x  x  2x x  4  x  x 2 2 2 2 2
 4x x  4  k  4  4  k  0 1 2 1 2 1 2 1 2 1 2 (hiển nhiên)
Vậy, với mọi giá trị của k, (d) luôn cắt (P) tại hai điểm phân biệt A và B có hoành độ x , x 1 2 thỏa điều kiện x  x  2. 1 2  3 3 x   y  9   1
b) Giải hệ phương trình  . 2 2 x
  2y  x  4y 2  2 2 2 2
 Ta có: 2  3x  6y  3x  12y  0  3x  3x  6y  12y  0 3.
 Lấy phương trình  
1  3, vế theo vế ta được: 3 3 2 2
x  y  3x  3x  6y  12y  9   3 2
x  x  x     3 2 3 3 1
y  6y  12y  8  0
 x  3  y  3 1
2  0  x  1  2  y  x  y  3 .
 x  3  y.
 Thay x  3  y vào phương trình 2 ta được:   y2 2 3
 2y  y  3  4y  0 y   1  x  2 2 3y 9y 6 0      . y   2  x  1 
 Vậy hệ phương trình có hai nghiệm 1;2;2;  1 . Câu 3. Điều kiện: x  .  2 2 2 Đặt t 
x  1  1  x  t  1, phương trình (1) trở thành: 2 2 2 2
t  1  2(m  1)t  m  m  2  0  t  2(m  1)t  m  m  3  0 (2) t  1  (l) 
a) Khi m  0, (1)  2
t  1  2t  2  0  t  3 (n)  2 2 2
Với t  3 ta có x  1  3  x  1  9  x  8  x  2  2
b) Phương trình (1) có bốn nghiệm phân biệt  phương trình (2) có hai nghiệm t  1,t  1 1 2 phân biệt  2   '  (m  1)    2
m  m  3  0 t    1  0 (*) 1  t  1  0  2 
Đưa về tổng tích và áp dụng định lý Vi-ét đối với phương trình (2) ta được:
NHÓM GIẢI ĐÊ: ThS. Trần Ngọc Đức Toàn – Thầy Nguyễn Văn Vũ – Thầy Hoàng Đức Vương  4  4    3   4  0 m    m m      3     3    (*)  (
 t  1)  (t  1)  0  t   t  2  0  2
 (m  1)  2  0 1 2 1 2       2 (
 t  1).(t  1)  0 t
 t  (t  t )  1  0   1 2   1 2 1 2
m  m  3  2(m 1)  1  0      m   0  4    m        m   1  0 m   0  3 m   0            m   0    m   4  0      m   4  m  4  (
 m  1)(m  4)  0        2   m   3m  4  0  m   1  0  m  1            m    4  0    
Vậy, m  4 thỏa yêu cầu bài toán. Câu 4.
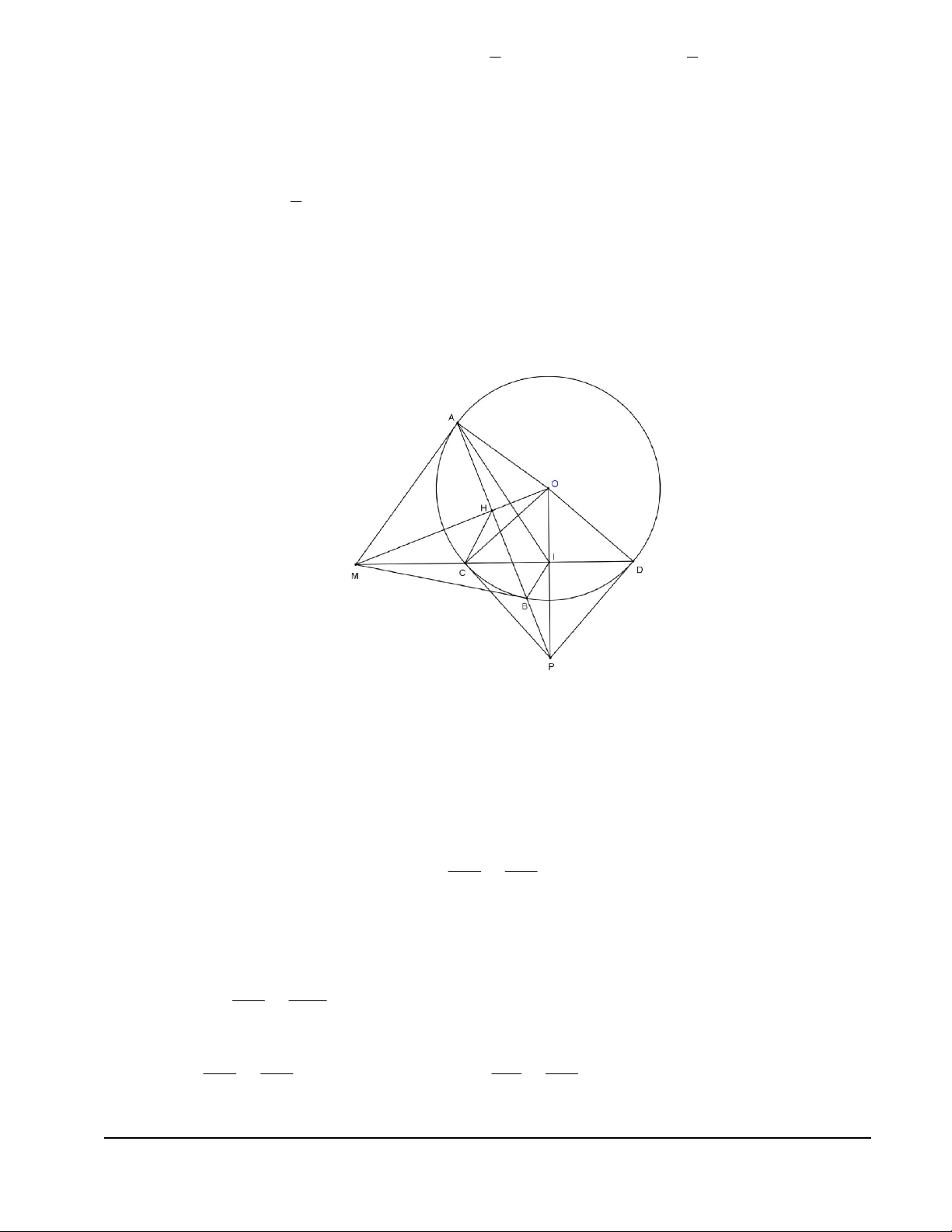
a) Chứng minh tứ giác MAIB nội tiếp.  0  0  0
 Ta có: MAO  90 , MIO  90 (do I là trung điểm CD), MBO  90 . Suy ra 5 điểm M, ,
A O, I, B cùng nhìn đoạn MO dưới một góc vuông. Do đó, 5 điểm M, ,
A O,I,B thuộc
đường tròn đường kính OM . Vậy tứ giác MAIB nội tiếp.
b) Chứng minh đường thẳng AB luôn đi qua một điểm cố định khi M di động trên tia Ct.   0
 Gọi giao điểm của tiếp tuyến tại C và tại D là P . Ta có: OCP  ODP  90 . Suy ra tứ giác
OCPD nội tiếp đường tròn đường kính OP . MH MC    Do 2
MH .MO  MA  MC .MD  
và CMH  OMD  CHOD nội tiếp. MD MO
 O,H,C,P,D   0
cùng thuộc đường tròn đường kính OP 0
 OHP  90 mà OHB  90 nên 3 điểm ,
A B, P thẳng hàng.
 Vậy khi M di động trên tia Ct thì AB luôn đi qua điểm P cố định. 2 MD HA c) Chứng minh  . 2 MC HC
Ta có: MH .MO  MC .MD (câu b) MH MC HC MC    MC  H  MO  D   . MD MO OD MO
NHÓM GIẢI ĐÊ: ThS. Trần Ngọc Đức Toàn – Thầy Nguyễn Văn Vũ – Thầy Hoàng Đức Vương  2 2  2 MC .OD H  C   Ta có: 2  OM  2 H
 A  MH.OH  2 2 2 HA MH.OH.OM MH.OH.OM MH.OM MC.MD MD       . 2 2 2 2 2 2 HC MC .OA MC .OH.OM MC MC MC 2 MD HA Vậy  . 2 MC HC Câu 5.
a) Theo bất đẳng thức cô si, ta có: 2 2 a b  c a b  c 2 a b  c    2 .  a   a  . b  c 4 b  c 4 b  c 4 2 2 2 b a  c b a  c b a  c    2 .  b   b  . a  c 4 a  c 4 a  c 4 2 2 2 c a  b c a  b c a  b    2 .  c   c  . a  b 4 a  b 4 a  b 4 2 2 2 a b c
a  b  c
a  b  c
ab  bc  ac 1 Do đó:  
 a  b  c     . b  c a  c a  b 2 2 2 2 a
  0;b  0;c  0 1  1  Vậy E   a   b  c
 a  b  c  . min 2  3
 ab  bc  ac  1  2 n 2 2 2 n n
b) Giả sử n  3  m  m  n  3  m  nm  n  3 . n k  k Đặt   3k m n , suy ra 3n k m n   
, mà m  n  m  n  3
 3  n  2k  n  2k  1.
 Xét n  2k  1 thì     n k k k  n 2 2 3 3 3 3 k 1 2.3k n m n m n            n   1   3k n
 2k  1  k  0;1   . n   3 
 Xét n  2k  2  n  k  2  k .   Do đó: n k k n k n k 2 n k 2 n             2   n k 2 2 3 3 3 3 3 3 1  8.3 . n k  2   
Theo bất đẳng thức Bernoulli thì n k 2 8.3 8.1 2 8. 1  2  n k 2      
 16n  16k  24.  
Suy ra 2n  16n  16k  24  8k  12  7n. Hơn nữa n  2k  2  8k  12  7n  14k  14 (vô lí)
Vậy n  1;n  3.
“Giữa thành công và thất bại có con sông gian khổ... trên con sông đó có cây cầu tên là sự cố gắng”
NHÓM GIẢI ĐÊ: ThS. Trần Ngọc Đức Toàn – Thầy Nguyễn Văn Vũ – Thầy Hoàng Đức Vương