-
Thông tin
-
Quiz
Đề thi tuyển sinh lớp 10 THPT 2023-2024 môn toán Sở GD Hưng Yên mã đề 110 (có đáp án và lời giải chi tiết)
Tổng hợp Đề thi tuyển sinh lớp 10 THPT 2023-2024 môn toán Sở GD Hưng Yên mã đề 110 (có đáp án và lời giải chi tiết) rất hay và bổ ích giúp bạn đạt điểm cao. Các bạn tham khảo và ôn tập để chuẩn bị thật tốt cho kỳ thi tốt nghiệp sắp đến nhé. Mời bạn đọc đón xem.
Chủ đề: Đề thi vào 10 môn Toán năm 2023-2024 872 tài liệu
Môn: Môn Toán 1.3 K tài liệu
Thông tin:
Tác giả:
Preview text:
SỞ GIÁO DỤC ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 HƯNG YÊN
NĂM HỌC: 2023 – 2024 Môn: TOÁN Mã đề 110
Khoá thi ngày: 03 tháng 6 năm 2023
Thời gian làm bài: 90 phút (không kể thời gian giao đề) Câu 1:
Tâm đường tròn nội tiếp tam giác là giao điểm của ba đường nào trong tam giác đó?
A. Ba đường trung tuyến.
B. Ba đường cao.
C. Ba đường phân giác.
D. Ba đường trung trực. Câu 2:
Cho đường tròn tâm O;4cm và đường thẳng a không có điểm chung với đường tròn. Gọi
h là khoảng cách từ tâm O tới đường thẳng a . Khẳng định nào sau đây đúng?
A. h 4 cm .
B. h 6 cm .
C. h 4 cm . D. h 4 cm . Câu 3:
Hàm số y ax b a 0 nghịch biến trên khi
A. b 0 .
B. a 0 .
C. b 0. D. a 0 . Câu 4:
Đẳng thức nào sau đây đúng?
A. sin50 cot40 .
B. sin50 cos40 .
C. sin50 cos50 .
D. sin50 tan 40. Câu 5:
Cho đường tròn O; R và O;r thoả mãn R r đồng thời R r OO R r . Kết luận nào sau đây đúng?
A. Hai đường tròn đó đựng nhau.
B. Hai đường tròn đó cắt nhau.
C. Hai đường tròn đó tiếp xúc ngoài.
D. Hai đường tròn đó tiếp xúc trong. Câu 6:
Diện tích xung quanh của hình nón có bán kính đáy r và đường sinh l là 1 1
A. rl .
B. rl .
C. 2rl . D. 2 r l . 2 3 Câu 7: Giá trị của 3 27 bằng A. 3 . B. 9 C. 3 . D. 9 . Câu 8:
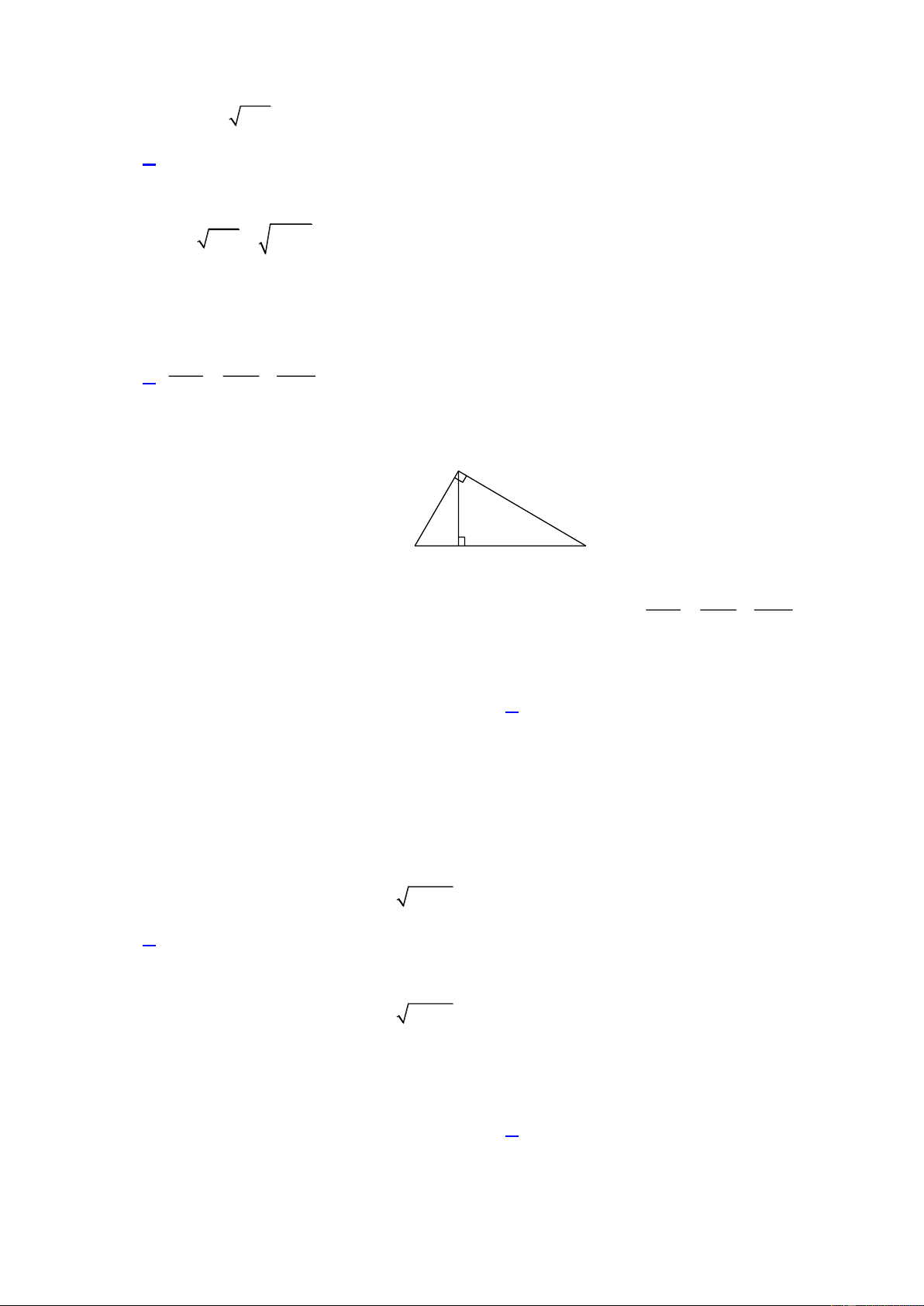
Cho tam giác ABC vuông tại A , đường cao AH . Hệ thức nào sau đây sai? A. 2
AB BH BC . B. 2
AC BC HC . 1 1 1 C. . D. 2
AH BH CH . 2 2 2 AB AC AH Câu 9:
Phương trình x 5y 7
nhận cặp số nào sau đây là nghiệm? A. 0 ;1 . B. 1 ;2 . C. 3; 2 . D. 2; 4 .
Câu 10: Điều kiện xác định của biểu thức x 10 là A. x 10 . B. x 10 . C. x 10 . D. x 10 .
7x 3y 11
Câu 11: Cho hệ phương trình có nghiệm ;
x y . Tổng x y bằng
4x y 9 Trang 1 A. 2 . B. 3 . C. 3 . D. 2 .
x y 1 Câu 12: Hệ phương trình có bao nhiêu nghiệm? x y 1
A. Vô nghiệm. B. Vô số nghiệm.
C. Một nghiệm. D. Hai nghiệm.
Câu 13: Trong các hàm số sau hàm số nào là hàm số bậc nhất? 2 A. y x .
B. y 1 2x . C. y . D. 2 y 2x . x
Câu 14: Tứ giác nào sau đây nội tiếp đường tròn? A. Hình thoi.
B. Hình bình hành. C. Hình thang. D. Hình chữ nhật.
Câu 15: Cho đường tròn tâm O có hai dây AB,CD không đi qua tâm. Biết rằng khoảng cách từ tâm O
đến hai dây là bằng nhau. Kết luận nào sau đây là đúng? A. 2 2
AB CD .
B. AB CD .
C. AB CD .
D. AB CD .
Câu 16: Hàm số nào sau đây đồng biến khi x 0 ?
A. y x 3 . B. 2 y 2x . C. 2 y 3 x . D. 2 y x .
Câu 17: Giá trị của x thỏa mãn x 2 là A. x 2 . B. x 4 . C. x 4 . D. x 2 .
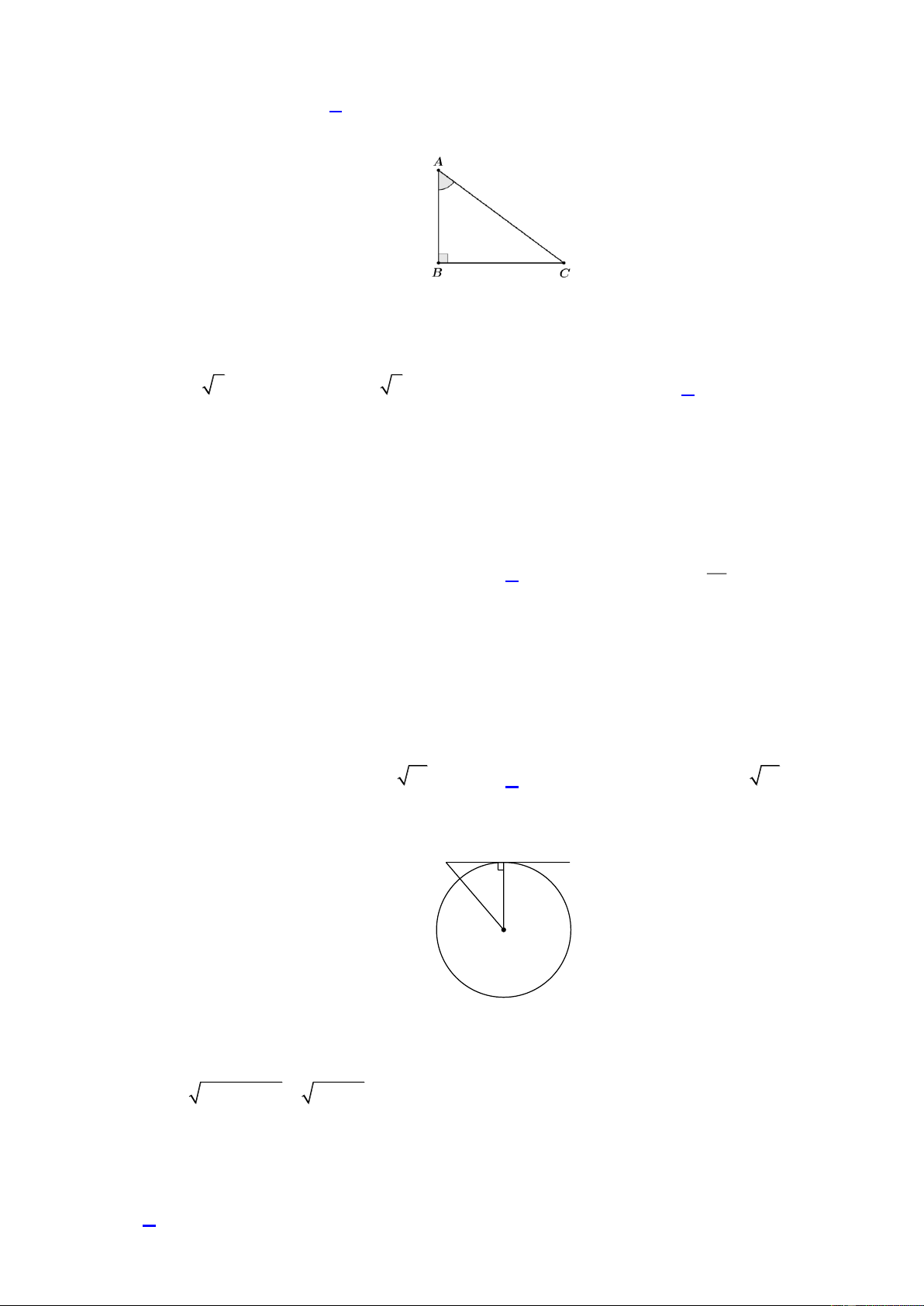
Câu 18: Cho tam giác ABC vuông tại B . Khẳng định nào sau đây đúng?
A. AB B . C tan A.
B. BC A . B tan A.
C. BC A . C tan A .
D. AB A . C tan A.
Câu 19: Phương trình nào dưới đây là phương trình bậc hai một ẩn? A. 2
x x 1 0 .
B. x x 1 0 . C. 4 2
x 2x 4 0 . D. 2 x 2023 0 .
Câu 20: Diện tích của mặt cầu có bán kính r 2cm bằng 32 A. 4 2 cm . B. 8 2 cm . C. 16 2 cm . D. 2 cm . 2
Câu 21: Cho đường tròn tâm O bán kính 4 cm và một điểm A cách O là 5 cm . Kẻ tiếp tuyến AB với
đường tròn ( B là tiếp điểm). Khi đó độ dài đoạn thẳng AB là bao nhiêu?
A. AB 9 cm . B. AB 21 cm . C. AB 3cm . D. AB 41 cm .
Câu 22: Cung AB của một đường tròn bán kính 6 cm có độ dài 2 cm . Số đo cung AB đó bằng A. 60 . B. 30 . C. 45. D. 90 .
Câu 23: Cho hàm số y 2
x m 3. Giá trị của tham số m để đồ thị hàm số đi qua điểm A2;5 là A. m 6. B. m 4 . C. m 9 . D. m 2 .
Câu 24: Tọa độ giao điểm của đồ thị hàm số y 2x 1 và y x 2 là A. 3 ; 1 . B. 1 ;2 . C. 1; 2 . D. 3;5 .
Câu 25: Gọi x ; x là nghiệm của phương trình 2
x 6x 1 0 . Tích x x bằng 1 2 1 2 A. 1. B. 2 . C. - 6 . D. - 1. Trang 2
Câu 26: Góc tạo bởi đường thẳng d : y 3x 2023 với trục Ox là A. 60 . B. 30 . C. 120 . D. 45.
Câu 27: Cho tam giác ABC vuông tại A đường cao AH và HB 2 cm ; BC 8 cm . Độ dài cạnh AB bằng A. 4 2 cm . B. 4cm . C. 4 3 cm . D. 6cm.
Câu 28: Rút gọn biểu thức 2 2
a 6a 9 a 6a 9 với 3
a 3 ta được kết quả bằng A. 6 . B. 18 . C. a . D. 2a .
Câu 29: Cho tam giác ABC vuông tại A đường cao AH 4 cm ; HC 8 cm . Độ dài cạnh BC bằng A. 10 cm . B. 10 2 cm . C. 10 3 cm . D. 8 cm .
Câu 30: Phương trình 2
x 4x 4m 8 0 (với m là tham số) có nghiệm bằng 2 . Khi đó m bằng A. 1. B. 1. C. 3 . D. 3 .
Câu 31: Cho AB là dây cung của đường tròn O;13cm và khoảng cách từ tâm O đến dây cung AB
bằng 5cm . Độ dài dây cung AB bằng A. 5cm . B. 24cm . C. 13cm . D. 12cm .
Câu 32: Parabol dưới đây là đồ thị của hàm số nào? y -1 1 x O -1 -2 A. 2
y x . B. 2
y x . C. 2 y 2 x . D. 2 y 2x .
Câu 33: Hai đường tròn O;6cm và O;5cm, với OO 11cm có số tiếp tuyến chung là A. 2 . B. 1. C. 3 . D. 4 .
Câu 34: Hai số có tổng S 6 và tích P 5
là nghiệm của phương trình nào dưới đây? A. 2
x - 6x + 5 = 0 . B. 2
x - 5x + 6 = 0 . C. 2
x - 5x - 6 = 0 . D. 2
x - 6x - 5 = 0 .
Câu 35: Biết 3 2 2 1 a b 2 với ( a, b là các số nguyên). Khi đó a b bằng A. 1. B. 4 . C. 3 . D. 2 .
Câu 36: Cho hai đường thẳng d : y x 2 và d : y 2m m x m m . Số giá trị của tham số 2 2 2 1
m để d và d song song với nhau là 2 1 A. 2 . B. 1. C. 0 . D. 3 .
Câu 37: Số giá trị nguyên của a để 3 a 12 a 6a 8 a 5 9 là A. 65. B. 63. C. 64 . D. 1. Trang 3
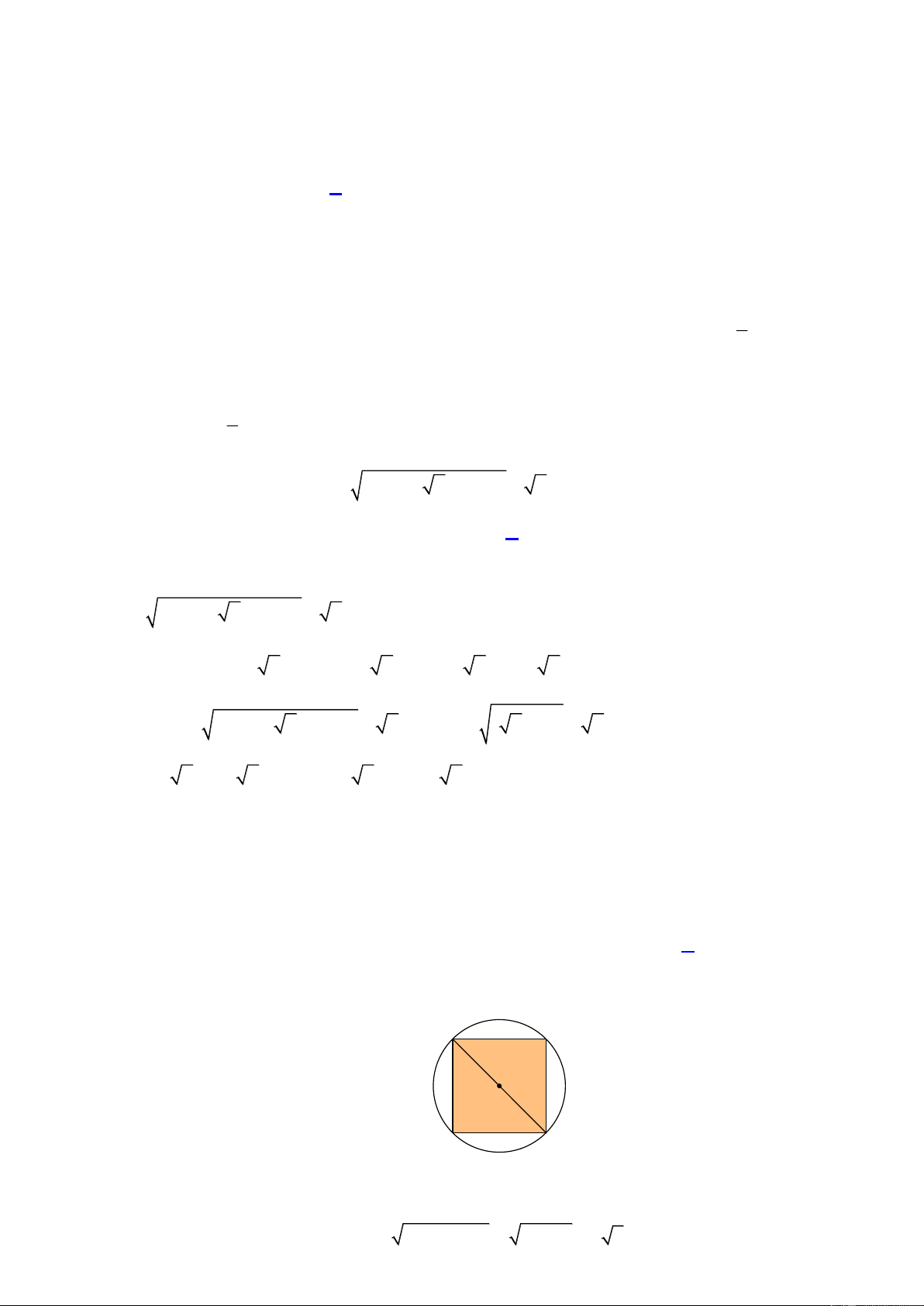
Câu 38: Cho hình vuông có cạnh 6 cm nội tiếp đường tròn O . Diện tích hình tròn O bằng A. 2 12 cm . B. 2 9 cm . C. 2 36 cm . D. 2 18 cm . 3
x y 2m 16
Câu 39: Cho hệ phương trình
có bao nhiêu giá trị nguyên của tham số m để hệ
x y 2m 4
phương trình có nghiệm ;
x y sao cho x 0 , y 0 ? A. 7 . B. 6 . C. 5 . D. 4 .
Câu 40: Cho đường tròn O có góc nội tiếp BAC bằng 100 ( B và C thuộc đường tròn). Số đo của góc BOC bằng A. 100 . B. 260 . C. 160 . D. 200 .
Câu 41: Một cột đèn vuông góc với mặt đất có bóng trên đó dài 8,5 m . Các tia nắng tạo với mặt đất
một góc bằng 43. Chiều cao của cột đèn là (làm tròn đến chữ số thập phân thứ hai) A. 6,22 m . B. 5,80 m . C. 7,93 m . D. 9,12 m .
Câu 42: Cho đường tròn O; 20cm và hai bán kính O ,
A OB vuông góc với nhau tại O . Một dây MN
cắt hai bán kính O ,
A OB lần lượt tại E, F sao cho ME EF FN . Độ dài dây MN là (Kết
quả làm tròn đến chữ số thập phân thứ hai) A. 37, 96cm . B. 37, 95cm . C. 37, 93cm . D. 37, 94cm .
Câu 43: Để ba đường thẳng d : y 6 5 ; x d
: y m 3 x ; m d
: y 3x 2 đồng quy thì giá trị 1 2 3
của tham số m bằng A. m 2 .
B. m 3 . C. m 3 . D. m 2 .
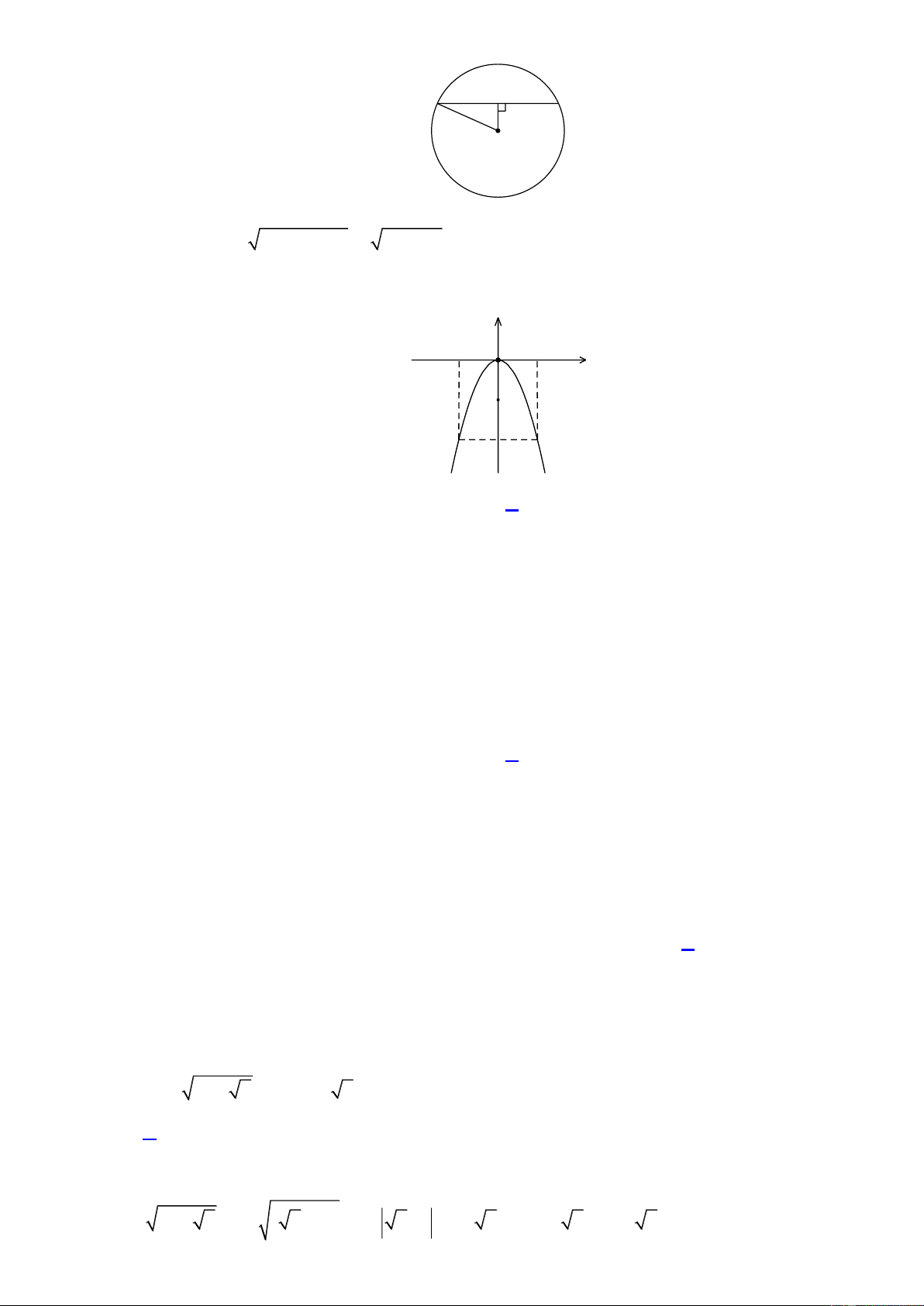
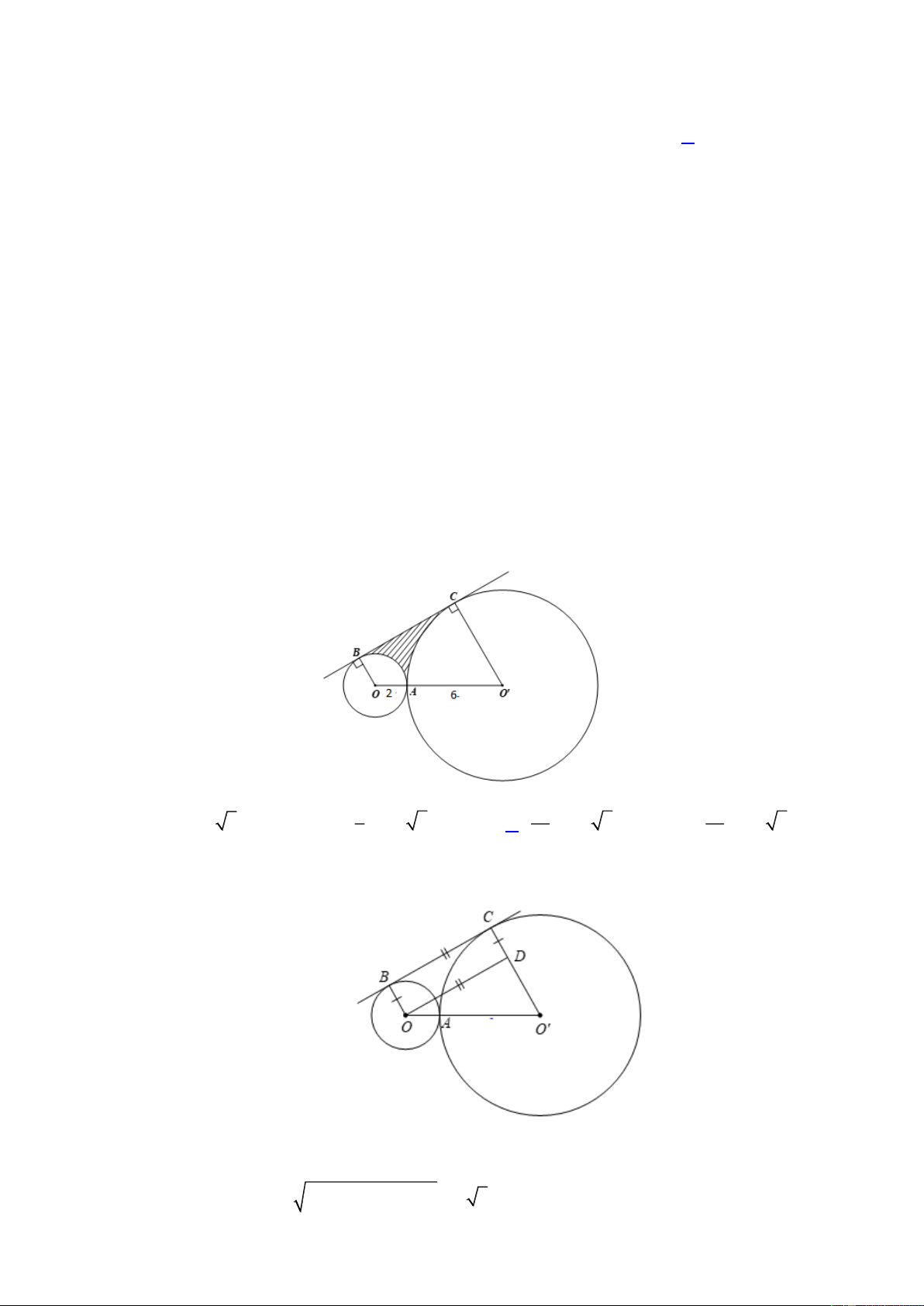
Câu 44: Cho hai đường tròn (O ; 2 cm)
và (O ; 6 cm) tiếp xúc ngoài nhau tại A , vẽ tiếp tuyến chung
ngoài BC của hai đường tròn ( B,C là tiếp điểm). Chu vi phần hình phẳng giới hạn bởi tiếp
tuyến chung BC và hai đường tròn trên là (Tham khảo hình vẽ) 8 10 10
A. 3 4 3 cm .
B. 4 3 cm . C.
4 3 cm. D. 2 3 cm. 3 3 3
Câu 45: Một chiếc ca-nô chạy trên sông xuôi dòng 108km và ngược dòng 63km thì hết 7 giờ. Một lần
khác cũng trong 7 giờ, ca-nô xuôi dòng 81km và ngược dòng 84km (Biết vận tốc ca-nô và
vận tốc dòng nước không đổi). Vận tốc dòng nước là A. 4km/h . B. 3km/h . C. 2km/h . D. 2,5km/h .
Câu 46: Cho phưong trình 3
x m 2 2
1 x 3m 4 x m 12 0 ( m là tham số). Hỏi có bao nhiêu
giá trị nguyên dương bé hơn 2023 của m để phương trình có 3 nghiệm phân biệt? Trang 4 A. 2018 . B. 2017 . C. 2022 . D. 2021.
Câu 47: Cho tam giác nhọn ABC nội tiếp O có AC 3. Kẻ tiếp tuyến xAy với O . Từ C kẻ
CM // xy M AB . Khẳng định nào sau đâu đúng?
A. AM.AB 9 .
B. AM.AB 6 .
C. AM.AB 18.
D. AM.AB 12 .
Câu 48: Để phương trình 2
x n x n m 2 2 2 1 2 2
m n 0 ( với ,
m n là tham số) có nghiệm thì giá trị của P . m n bằng A. 4 . B. 2 . C. 1. D. 4 .
Câu 49: Cho ba số thực a, b, c thỏa mãn a 2b 3c 28 . Giá trị nhỏ nhất của biểu thức 75 9 4
A a b c là a 2b c A. 29 . B. 26 . C. 28 . D. 27 .
Câu 50: Cho Parabol P 2
: y x và đường thẳng d : y x m . Điều kiện của m để d cắt P tại
hai điểm phân biệt nằm về hai phía của trục tung là A. m 1 .
B. m 0. C. m 1 . D. m 0 .
-------------------------------49Hết49----------------------------------- Trang 5 HƯỚNG DẪN GIẢI Câu 1:
Tâm đường tròn nội tiếp tam giác là giao điểm của ba đường nào trong tam giác đó?
A. Ba đường trung tuyến.
B. Ba đường cao.
C. Ba đường phân giác.
D. Ba đường trung trực. Lời giải
Tâm đường tròn nội tiếp tam giác là giao điểm của ba đường phân giác. Câu 2:
Cho đường tròn tâm O;4cm và đường thẳng a không có điểm chung với đường tròn. Gọi
h là khoảng cách từ tâm O tới đường thẳng a . Khẳng định nào sau đây đúng?
A. h 4 cm .
B. h 6 cm .
C. h 4 cm . D. h 4 cm . Lời giải
Đường thẳng a không có điểm chung với đường tròn O;4cm nên khoảng cách từ tâm O tới
đường thẳng a lớn hơn bán kính Suy ra: h 4 cm . Câu 3:
Hàm số y ax b a 0 nghịch biến trên khi
A. b 0 .
B. a 0 .
C. b 0. D. a 0 . Lời giải
Hàm số y ax b a 0 nghịch biến trên khi a 0 . Câu 4:
Đẳng thức nào sau đây đúng?
A. sin50 cot40 .
B. sin50 cos40 .
C. sin50 cos50 .
D. sin50 tan 40. Lời giải
Ta có: 50 40 90 nên sin50 cos40 . Câu 5:
Cho đường tròn O; R và O;r thoả mãn R r đồng thời R r OO R r . Kết luận nào sau đây đúng?
A. Hai đường tròn đó đựng nhau.
B. Hai đường tròn đó cắt nhau.
C. Hai đường tròn đó tiếp xúc ngoài.
D. Hai đường tròn đó tiếp xúc trong. Lời giải
Đường tròn O; R và O;r thoả mãn R r đồng thời R r OO R r nên hai đường tròn đó cắt nhau. Câu 6:
Diện tích xung quanh của hình nón có bán kính đáy r và đường sinh l là 1 1
A. rl .
B. rl .
C. 2rl . D. 2 r l . 2 3 Lời giải Trang 6
Hình nón có bán kính đáy r và đường sinh l thì có diện tích xung quanh là: S rl . xq Câu 7: Giá trị của 3 27 bằng A. 3 . B. 9 C. 3 . D. 9 . Lời giải Ta có 3 3 3 27 3 3 . Câu 8:
Cho tam giác ABC vuông tại A , đường cao AH . Hệ thức nào sau đây sai? A. 2
AB BH BC . B. 2
AC BC HC . 1 1 1 C. . D. 2
AH BH CH . 2 2 2 AB AC AH Lời giải A B H C 1 1 1
Trong tam giác ABC vuông tại A , đường cao AH , hệ thức sai là . 2 2 2 AB AC AH Câu 9:
Phương trình x 5y 7
nhận cặp số nào sau đây là nghiệm? A. 0 ;1 . B. 1 ;2 . C. 3; 2 . D. 2; 4 . Lời giải
Phương trình x 5y 7
là phương trình bậc nhất hai ẩn, để xác định nghiệm thì ta thế từng
cặp nghiệm của 4 phương án vào phương trình. Ta có 3 5.2 7
nên 3;2 là nghiệm của phương trình.
Câu 10: Điều kiện xác định của biểu thức x 10 là A. x 10 . B. x 10 . C. x 10 . D. x 10 . Lời giải
Điều kiện xác định của biểu thức x 10 là x 10 0 x 1 0 .
7x 3y 11
Câu 11: Cho hệ phương trình có nghiệm ;
x y . Tổng x y bằng
4x y 9 A. 2 . B. 3 . C. 3 . D. 2 . Lời giải Trang 7
7x 3y 11
7x 3y 11 19 x 38 x 2 x 2
4x y 9 12
x 3y 27
4x y 9 4.2 y 9 y 1
Tổng x y 2 1 3 .
x y 1
Câu 12: Hệ phương trình có bao nhiêu nghiệm? x y 1
A. Vô nghiệm. B. Vô số nghiệm.
C. Một nghiệm. D. Hai nghiệm. Lời giải
x y 1 x y 1 Ta có: x y 1 x y 1 1 1 1 Vì
nên hệ phương trình có vô số nghiệm. 1 1 1
Câu 13: Trong các hàm số sau hàm số nào là hàm số bậc nhất? 2 A. y x .
B. y 1 2x . C. y . D. 2 y 2x . x Lời giải
Hàm số bậc nhất có dạng y ax b a 0 nên y 1 2x là hàm số bậc nhất.
Câu 14: Tứ giác nào sau đây nội tiếp đường tròn? A. Hình thoi. B. Hình bình hành. C. Hình thang. D. Hình chữ nhật. Lời giải
Hình chữ nhật có tổng hai góc đối bằng 180 nên hình chữ nhật nội tiếp đường tròn.
Câu 15: Cho đường tròn tâm O có hai dây AB,CD không đi qua tâm. Biết rằng khoảng cách từ tâm O
đến hai dây là bằng nhau. Kết luận nào sau đây là đúng? A. 2 2
AB CD .
B. AB CD .
C. AB CD .
D. AB CD . Lời giải
Trong đường tròn tâm O , hai dây AB,CD cách đều tâm thì bằng nhau nên AB CD .
Câu 16: Hàm số nào sau đây đồng biến khi x 0 ?
A. y x 3 . B. 2 y 2x . C. 2 y 3 x . D. 2 y x . Lời giải Hàm số 2
y ax a 0 có a 0 thì hàm số đồng biến khi x 0 Nên hàm số 2
y 2x đồng biến khi x 0 .
Câu 17: Giá trị của x thỏa mãn x 2 là A. x 2 . B. x 4 . C. x 4 . D. x 2 . Lời giải Có x 2
x 4 x 4 Trang 8
Câu 18: Cho tam giác ABC vuông tại B . Khẳng định nào sau đây đúng?
A. AB B . C tan A.
B. BC A . B tan A.
C. BC A .
C tan A .
D. AB A . C tan A. Lời giải
Tam giác ABC vuông tại B nên BC A . B tan A.
Câu 19: Phương trình nào dưới đây là phương trình bậc hai một ẩn? A. 2
x x 1 0 .
B. x x 1 0 . C. 4 2
x 2x 4 0 . D. 2 x 2023 0 . Lời giải
Phương trình bậc hai một có dạng 2
ax bx c 0 với a 0 nên phương trình 2 x 2023 0 là
phương trình bậc hai một ẩn.
Câu 20: Diện tích của mặt cầu có bán kính r 2cm bằng 32 A. 2 4 cm 2 cm . B. 2 8 cm . C. 2 16 cm . D. 2 cm . 2 Lời giải Diện tích mặt cầu là: 2 2
S R S 2 4 4 2 16 cm .
Câu 21: Cho đường tròn tâm O bán kính 4 cm và một điểm A cách O là 5 cm . Kẻ tiếp tuyến AB với
đường tròn ( B là tiếp điểm). Khi đó độ dài đoạn thẳng AB là bao nhiêu?
A. AB 9 cm . B. AB 21 cm . C. AB 3cm . D. AB 41 cm . Lời giải A B 4 5 O
Vì AB là tiếp tuyến và B là tiếp điểm nên OB R 4cm và AB OB tại B
Áp dụng định lý Pytago cho tam giác ABO vuông tại B ta được: 2 2 2 2
AB OA OB 5 4 3cm Vậy AB 3cm .
Câu 22: Cung AB của một đường tròn bán kính 6 cm có độ dài 2 cm . Số đo cung AB đó bằng A. 60 . B. 30 . C. 45. D. 90 . Trang 9 Lời giải . . R n l.180 2 .180
Áp dụng công thức tính độ dài cung tròn: l n 60 180 .R . .6
Câu 23: Cho hàm số y 2
x m 3. Giá trị của tham số m để đồ thị hàm số đi qua điểm A2;5 là A. m 6. B. m 4 . C. m 9 . D. m 2 . Lời giải
Đồ thị hàm số y 2
x m 3 đi qua điểm A2;5 x 2; y 5 thay vào hàm số 5 2
.2 m3 5 4
m3 m 6 .
Câu 24: Tọa độ giao điểm của đồ thị hàm số y 2x 1 và y x 2 là A. 3 ; 1 . B. 1 ;2 . C. 1; 2 . D. 3;5 . Lời giải
Hoành độ giao điểm của hàm số y 2x 1 và y x 2 là nghiệm của phương trình
2x 1 x 2
2x x 21 x 3
Thay x 3 vào y 2x 1 ta được: y 2.3 1 y 5
Vậy tọa độ giao điểm của y 2x 1 và y x 2 là 3;5 .
Câu 25: Gọi x ; x là nghiệm của phương trình 2
x + 6x - 1= 0 . Tích x x bằng 1 2 1 2 A. 1. B. 2 . C. - 6 . D. - 1. Lời giải Phương trình 2
x + 6x - 1= 0 có hai nghiệm phân biệt x ; x vì ac 1. 1 1 0 1 2
Theo định lí Viet ta có x x 1 . 1 2
Câu 26: Góc tạo bởi đường thẳng d : y 3x 2023 với trục Ox là A. 60 . B. 30 . C. 120 . D. 45. Lời giải
Ta có d : y 3x 2023 có hệ số góc a 3 0 nên tan 3 60 .
Câu 27: Cho tam giác ABC vuông tại A đường cao AH và HB 2 cm ; BC 8 cm . Độ dài cạnh AB bằng A. 4 2 cm . B. 4cm . C. 4 3 cm . D. 6cm. Lời giải Trang 10 A B H C
Vì tam giác ABC vuông tại A đường cao AH nên ta có 2
AB BH.BC 2.8 16 Suy ra AB 4 cm .
Câu 28: Rút gọn biểu thức 2 2
a 6a 9 a 6a 9 với 3
a 3 ta được kết qủa bằng A. 6 . B. 18 . C. a . D. 2a . Lời giải 2 2
Ta có: a 3 a 3 a 3 a 3 a 3 0 Với 3
a 3 thì
a 3 a 3 a 3 3 a 6 . a 3 0
Câu 29: Cho tam giác ABC vuông tại A đường cao AH 4 cm ; HC 8cm . Độ dài cạnh BC bằng A. 10 cm . B. 10 2 cm . C. 10 3 cm . D. 8 cm . Lời giải A B H C
Vì tam giác ABC vuông tại A đường cao AH nên ta có: 2 2 AH 4 2
AH BH.CH BH 2 cm CH 8
Suy ra BC BH HC 2 8 10 cm
Câu 30: Phương trình 2
x 4x 4m 8 0 ( với m là tham số) có nghiệm bằng 2 . Khi đó m bằng A. 1. B. 1. C. 3 . D. 3 . Lời giải Phương trình 2
x 4x 4m 8 0 có nghiệm bằng 2 nên: 2
2 4.2 4m 8 0 4 4m 0 m 1 .
Câu 31: Cho AB là dây cung của đường tròn O;13cm và khoảng cách từ tâm O đến dây cung AB
bằng 5cm . Độ dài dây cung AB bằng A. 5cm . B. 24cm . C. 13cm . D. 12cm . Lời giải Trang 11 A H B O Ta có: 2 2 2 2 AH = OA - OH =
13 - 5 = 12 AB 2AH 2.12 24cm
Câu 32: Parabol dưới đây là đồ thị của hàm số nào? y -1 1 x O -1 -2 A. 2
y x . B. 2
y x . C. 2 y 2 x . D. 2 y 2x . Lời giải
Gọi parabol cần tìm có dạng 2
y ax a 0.
Vì parabol đi qua A1; 2 . Thay x 1; y 2
vào phương trình Parabol ta được 2 2 .1 a a 2
. Vậy Parabol cần tìm có dạng 2 y 2 x .
Câu 33: Hai đường tròn O;6cm và O ;5cm , với OO 11cm có số tiếp tuyến chung là A. 2 . B. 1. C. 3 . D. 4 . Lời giải
Có OO R r 6cm 5cm 11cm .
Hai đường tròn trên tiếp xúc ngoài nên số tiếp tuyến chung là 3 .
Câu 34: Hai số có tổng S 6 và tích P 5
là nghiệm của phương trình nào dưới đây? A. 2
x - 6x + 5 = 0 . B. 2
x - 5x + 6 = 0 . C. 2
x - 5x - 6 = 0 . D. 2
x - 6x - 5 = 0 . Lời giải
Hai số có tổng S 6 và tích P 5
là nghiệm của phương trình 2
x Sx P 0 hay 2
x - 6x - 5 = 0
Câu 35: Biết 3 2 2 1 a b 2 với ( a, b là các số nguyên). Khi đó a b bằng A. 1. B. 4 . C. 3 . D. 2 . Lời giải 2 3 2 2 1 2 1
1 2 1 1 2 11 2 0 1 2 Trang 12
Suy ra a 0;b 1 a b 1 .
Câu 36: Cho hai đường thẳng d : y x 2 và d : y 2m m x m m . Số giá trị của tham số 2 2 2 1
m để d và d song song với nhau là 2 1 A. 2 . B. 1. C. 0 . D. 3 . Lời giải
Để hai đường thẳng song song thì m 1 2 2 a a 2m m 1 2m m 1 0 m 12m 1 0 1 m 2 2 b b
m m 2
m m 2 0 m 1m 2 0 2
m 1;m 2 1 Vậy m
thì hai đường thẳng trên song song. Số giá trị của m là 1. 2
Câu 37: Số giá trị nguyên của a để 3 a 12 a 6a 8 a 5 9 là A. 65. B. 63. C. 64 . D. 1. Lời giải
3 a 12 a 6a 8 a 5 9 . ĐKXĐ: a 0 Ta có: a
a a a a a
a a 3 12 6 8 6 12 8 2
Do đó: a a a a a 3 3 3 12 6 8 5 9 2 a 5 9
a 2 a 5 9 2 a 16 a 8 0 a 64
Do a là số nguyên nên a 0;1;2;...;6 3 .
Vậy có 64 giá trị của a .
Câu 38: Cho hình vuông có cạnh 6 cm nội tiếp đường tròn O . Diện tích hình tròn O bằng A. 2 12 cm . B. 2 9 cm . C. 2 36 cm . D. 2 18 cm . Lời giải A B O 6 cm D C
Xét hình vuông ABCD
Theo định lý pytago ta có: 2 2 2 2
AC CD AD 6 6 6 2 m c Trang 13 AC 6 2
Vì AC là đường kính của đường tròn O nên R 3 2 cm 2 2 2
Vậy diện tích hình tròn O là: 2
S .R .3 2 18 2 cm 3
x y 2m 16
Câu 39: Cho hệ phương trình
có bao nhiêu giá trị nguyên của tham số m để hệ
x y 2m 4
phương trình có nghiệm ;
x y sao cho x 0 , y 0 ? A. 7 . B. 6 . C. 5 . D. 4 . Lời giải 3
x y 2m 16
4x 4m 20 x m 5 Ta có:
x y 2m 4
x y 2m 4 y m 1
Hệ phương trình có nghiệm x; y sao cho x 0 , y 0 nên ta có:
x m 5 0 m 5 1 m 5
y m 1 0 m 1
Vì m nên m 0;1;2;3;4; 5
Câu 40: Cho đường tròn O có góc nội tiếp BAC bằng 100 ( B và C thuộc đường tròn). Số đo của góc BOC bằng A. 100 . B. 260 . C. 160 . D. 200 . Lời giải A B 100° O C m
Ta có: BAC 100 sđBmC 200 sđBAC 360 200 160 BOC 160 .
Câu 41: Một cột đèn vuông góc với mặt đất có bóng trên đó dài 8,5 m . Các tia nắng tạo với mặt đất
một góc bằng 43. Chiều cao của cột đèn là (làm tròn đến chữ số thập phân thứ hai) A. 6,22 m . B. 5,80 m . C. 7,93 m . D. 9,12 m . Lời giải Trang 14 B 43° A 8,5 m C Xét AB
C A 90 theo hệ thức giữa cạnh và góc trong tam giác vuông, ta có: AB A .
C tan C AB 8,5.tan 43 7,93m .
Câu 42: Cho đường tròn ;
O 20cm và hai bán kính O ,
A OB vuông góc với nhau tại O . Một dây MN
cắt hao bán kính O ,
A OB lần lượt tại E, F sao cho ME EF FN . Độ dài dây MN là (Kết
quả làm tròn đến chữ số thập phân thứ hai) A. 37,96cm . B. 37, 95cm . C. 37, 93cm . D. 37,94cm . Lời giải A B E H F M N O
Kẻ OH vuông góc với MN HM HN
Lại có ME EF FN HE HF Xét F
OE vuông tại O có đường cao OH đồng thời là đường trung tuyến nên F OE vuông
cân tại O EFO 45 Do đó OHF
vuông cân tại H OH HF HE
Đặt OH HF HE xcm, x 0
Ta có: ME FE HN 2x HN 3x Xét OHN
vuông tại H , áp dụng định lí Py-ta-go có 2 2 2
OH HN ON 2 2 2
x 9x 20 2 10x 400 2
x 40 x 2 10 cm , do x 0
Vậy MN 2HN 6x 12 10 37, 95cm. Trang 15
Câu 43: Để ba đường thẳng d : y 6 5 ; x d
: y m 3 x ; m d
: y 3x 2 đồng quy thì giá trị 1 2 3
của tham số m bằng A. m 2 .
B. m 3 . C. m 3 . D. m 2 . Lời giải
Tọa độ giao điểm của đường thẳng d và d là nghiệm của hệ phương trình sau: 3 1
y 6 5x
6 5x 3x 2 x 1
y 3x 2
y 3x 2 y 1
Để ba đường thẳng d : y 6 5 ; x d
: y m 3 x ; m d
: y 3x 2 đồng quy thì tọa độ 1 2 3
giao điểm của đường thẳng d và d thỏa mãn phương trình đường thẳng d 2 3 1
Thay x 1, y 1 vào phương trình d ta được 1 m 31 m 1 m 3 m m 2 2
Vậy với m 2 thỏa mãn điều kiện bài.
Câu 44: Cho hai đường tròn O;2cm
và O ;6cm tiếp xúc ngoài nhau tại A , vẽ tiếp tuyến chung
ngoài BC của hai đường tròn ( B,C là tiếp điểm). Chu vi phần hình phẳng giới hạn bởi tiếp
tuyến chung BC và hai đường tròn trên là (Tham khảo hình vẽ) 8 10 10
A. 3 4 3 cm .
B. 4 3 cm . C.
4 3 cm. D. 2 3 cm. 3 3 3 Lời giải Kẻ OD O C
Tứ giác OBCD là hình chữ nhật 2 2
Suy ra : BC OD 6 2 6 2 4 3 cm Trang 16 O D 4 1 Xét ODO
vuông tại D , ta có: sin DOO OO 8 2 DOO 30 ; OO D
60 BOO 120 sđ AC 60 ; sđ AB 120 .
Chu vi phần hình phẳng giới hạn bởi tiếp tuyến chung BC và hai đường tròn trên là . . R n .R .n .2.120 .6.60 10 l
l BC BC 4 3 4 3 cm . AB AC 180 180 180 180 3
Câu 45: Một chiếc ca-nô chạy trên sông xuôi dòng 108km và ngược dòng 63km thì hết 7 giờ. Một lần
khác cũng trong 7 giờ, ca-nô xuôi dòng 81km và ngược dòng 84km (Biết vận tốc ca-nô và vận
tốc dòng nước không đổi). Vận tốc dòng nước là A. 4 km/h . B. 3km/h . C. 2 km/h . D. 2,5km/h . Lời giải
Gọi vận tốc thực của ca-nô là x km/h , vận tốc của dòng nước là y km/h , x y 0 . 108 63
Thời gian ca-nô xuôi dòng 108km và ngược dòng 63km lần lượt là ; (giờ)
x y x y 81 84
Thời gian ca-nô xuôi dòng 81km và ngược dòng 84km lần lượt là ; (giờ)
x y x y 108 63 7
x y x y
Theo bài ta có hệ phương trình: I 81 84 7
x y x y 3.108 3.63 324 189 81 84 1 1 21 21 7
x y x y
x y x y
x y x y x y 27 I 4.81 4.84 324 336 147 1 1 28 28 7
x y x y
x y x y x y
x y 21
x y 27 x 24 Suy ra
(thỏa mãn). Vậy vận tốc dòng nước là 3km/h .
x y 21 y 3
Câu 46: Cho phưong trình 3
x m 2 2
1 x 3m 4 x m 12 0 ( m là tham số). Hỏi có bao nhiêu
giá trị nguyên dương bé hơn 2023 của m để phương trình có 3 nghiệm phân biệt? A. 2018 . B. 2017 . C. 2022 . D. 2021. Lời giải 3
x m 2 2
1 x 3m 4 x m 12 0 1 Vì 1 2m
1 3m 4 m 12 0 nên phương trình
1 có một nghiệm x 1. Chia 3
x m 2 2
1 x 3m 4 x m 12 0 cho x 1 ta được 2
x 2mx m 12 Trang 17
Như vậy phương trình
1 được viết thành: x 1 2
x 2mx m 12 0 x 1 0 x 1 2
x 2mx m 12 0 2
x 2mx m 12 0 2 Để phương trình
1 cho có 3 nghiệm phân biệt thì phương trình 2 cần có hai nghiệm phân biệt khác 1. 2 0
m m 12 0
m 3m 4 0 2 1 2 .
m 1 m 12 0 13 m 0 m 3 1
Ta có m 3m 4 0 m 3 hoặc m 4
Số giá trị nguyên dương bé hơn 2023 của m để phương trình có 3 nghiệm phân biệt là 5 ; 6 ;
7 ; .... 2022 và m 13.
Vậy có tất cả: 2022 5 11 2017 giá trị của m thỏa mãn bài toán.
Câu 47: Cho tam giác nhọn ABC nội tiếp O có AC 3. Kẻ tiếp tuyến xAy với O . Từ C kẻ
CM // xy M AB. Khẳng định nào sau đâu đúng?
A. AM.AB 9 .
B. AM.AB 6 .
C. AM.AB 18.
D. AM.AB 12 . Lời giải x A y 3 B O M C
Có xy // CM nên xAM AMC (hai góc so le trong) 1
Có xAM ACB
sđ AB , suy ra ACB AMC 2 Xét A CBvà A
MC có: BAC chung; ACB AMC (cmt) Suy ra A CB∽ A MC (g.g) Do đó: AB AC 2 2 AC A . B AM A .
B AM 3 9 . AC AM
Câu 48: Để phương trình 2
x n x n m 2 2 2 1 2 2
m n 0 ( với ,
m n là tham số) có nghiệm thì giá trị của P . m n bằng A. 4 . B. 2 . C. 1. D. 4 . Lời giải Xét phương trình 2
x n x m m 2 2 2 1 2 2
m n 0 có Trang 18
n 2 n m 2 2 1 2 2 m n 2 2 2 2 2
n 2n 1 4n 2mn m n 2
n n 2 2 2 1
m 2mn n n
1 m n
Để phương trình có nghiệm kép thì 0 n 1 0 n 1
n 2 m n2 1 0 m n 0
m n 1
Vậy P mn 1. 1 1 .
Câu 49: Cho ba số thực dương a, b, c thỏa mãn a 2b 3c 28 . Giá trị nhỏ nhất của biểu thức 75 9 4
A a b c là a 2b c A. 29 . B. 26 . C. 28 . D. 27 . Lời giải 75 9 4
3a 75 b 9 c 4 a b 3c
Ta có A a b c a 2b c 4 a 2 2b 4 c 4 2 4 75 9 4
3a 75 b 9 c 4 1
A a b c .
a 2b 3c a 2b c 4 a 2 2b 4 c 4
Áp dụng BĐT cosi cho các cặp số dương ta được: 3a 75 3a 75 b 9 b 9 c 4 c 4 2. . 15; 2. . 3; 2 . 2 4 a 4 a 2 2b 2 2b 4 c 4 c
3a 75 b 9 c 4 Suy ra 15 3 2 20 4 a 2 2b 4 c
a,b,c 0; a 2b 3c 28 3a 75 a 10 4 a
Dấu " " xảy ra khi b 9 b 3 (1) 2 2b c 4 c 4 4 c 1 1
Lại có a 2b 3c 28 nên .a 2b 3c .28 7 4 4
Dấu " " xảy ra khi a 2b 3c 28 (2)
Từ (1) và (2) suy ra A 20 7 A 27 . Dấu " " xảy ra khi a 10;b 3; c 4.
Vậy GTNN của A bằng 27 khi a 10;b 3; c 4.
Câu 50: Cho Parabol P 2
: y x và đường thẳng d : y x m . Điều kiện của m để d cắt P tại
hai điểm phân biệt nằm về hai phía của trục tung là Trang 19 A. m 1 .
B. m 0. C. m 1 . D. m 0 . Lời giải
Hoành độ giao điểm của Parabol P 2
: y x và đường thẳng d : y x m là nghiệm của phương trình: 2
x x m , hay 2
x x m 0 1 .
Để để d cắt P tại hai điểm phân biệt nằm về hai phía của trục tung thì phương trình 1
cần có hai nghiệm x ; x trái dấu 1.m 0 m 0 m 0 . 1 2
---------------------------49Hết49-------------------------------- Trang 20