SỞ GD&ĐT VĨNH PHÚC
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN NĂM HỌC 2017-2018 ĐỀ THI MÔN: TOÁN ĐỀ CHÍNH THỨC
Dành cho thí sinh thi chuyên Toán, chuyên Tin học
Thời gian làm bài: 150 phút, không kể thời gian giao đề —————————
Câu 1 (2,0 điểm). Cho phương trình 2 2
x  2(m 1)x  2m  3m 1  0 , trong đó m là tham số, x là ẩn số.
a) Tìm tất cả các giá trị của m để phương trình có nghiệm. 9
b) Giả sử phương trình đã cho có hai nghiệm là x , x . Chứng minh rằng x  x  x x  . 1 2 1 2 1 2 8 2
2x  xy 1
Câu 2 (2,0 điểm). Cho hệ phương trình 
, trong đó m là tham số và x, y là 2 2
4x  4xy  y  m các ẩn số.
a) Giải hệ phương trình với m  7 .
b) Tìm tất cả các giá trị của m để hệ phương trình có nghiệm.
Câu 3 (3,0 điểm). Cho hình thang ABCD với AD, BC là hai cạnh đáy, BC  AD , BC  BD  1,
AB  AC , CD  1,   0
BAC  BDC  180 , E là điểm đối xứng với D qua đường thẳng BC.
a) Chứng minh rằng 4 điểm A, C, E, B cùng nằm trên một đường tròn và   BEC  2AEC .
b) Đường thẳng AB cắt đường thẳng CD tại điểm K , đường thẳng BC cắt đường thẳng AE tại
điểm F . Chứng minh rằng FA  FD và đường thẳng FD tiếp xúc với đường tròn ngoại tiếp tam giác ADK .
c) Tính độ dài cạnh CD.
Câu 4 (2,0 điểm). Cho phương trình 2 2 2
x  y  z  3xyz (1). Mỗi bộ số  x, y, z trong đó x, y, z là
các số nguyên dương thỏa mãn (1) được gọi là một nghiệm nguyên dương của phương trình (1).
a) Tìm tất cả các nghiệm nguyên dương có dạng x, y, y của phương trình (1).
b) Chứng minh rằng tồn tại nghiệm nguyên dương a,b,c của phương trình (1) và thỏa mãn
điều kiện mina; ; b 
c  2017 . Trong đó kí hiệu min ; a ; b 
c là số nhỏ nhất trong ba số a, b, . c
Câu 5 (1,0 điểm). Cho số tự nhiên n  1 và n  2 số nguyên dương a , a ,...,a thỏa mãn điều 1 2 n2
kiện 1  a  a  ...  a
 3n . Chứng minh rằng tồn tại hai số a , a (1  j  i  n  2;i, j  ) sao 1 2 n2 i j
cho n  a  a  2n . i j ---Hết---
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh …………………………………………………….. Số báo danh ……….. SỞ GDĐT VĨNH PHÚC
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN NĂM HỌC 2017 – 2018
HƯỚNG DẪN CHẤM MÔN: TOÁN
(Đáp án gồm 05 trang)
(Dành cho chuyên Toán, chuyên Tin học)
Câu 1 (2,0 điểm). Cho phương trình 2 2
x  2(m 1)x  2m  3m 1  0 , trong đó m là tham số, x là ẩn số. Nội dung Điểm
1a) Tìm tất cả các giá trị của m để phương trình có nghiệm. 1,00 PT có nghiệm 2 2
  '  (m 1)  (2m  3m 1)  0 0,25 2
 m  m  0  m(m 1)  0 0,25 m  0  m 1  0 0  m  1 m  0      m  0 m 1 0     0,25   m 1 m  0  m 1  0  m  1 0,25
1b) Giả sử phương trình đã cho có hai nghiệm là x , x . Chứng minh rằng 1 2 9 1,00
x  x  x x  . 1 2 1 2 8
x  x  2(m 1) Theo Viet ta có: 1 2  2
x .x  2m  3m 1  0,25 1 2 2  1  9 2  P |
 x  x  x .x || 2m  m 1| 2 m   1 2 1 2   0,25  4  16 2 1 1 3  1  9
Có 0  m  1    m    m     0,25 4 4 4  4  16 2  9 1    9 1 Suy ra P  2  m      
, dấu bằng xảy ra khi m  . 0,25 16 4    8   4 2
2x  xy 1
Câu 2 (2,0 điểm). Cho hệ phương trình 
, trong đó m là tham số và x, y là 2 2
4x  4xy  y  m các ẩn số. Nội dung Điểm
2a) Giải hệ phương trình với m  7 . 1,00 2   2 2x 1
2x  xy 1   y Với m=7 ta có:    x
(do x  0 không thỏa mãn). 0,25 2 2
4x  4xy  y  7  2 2
4x  4xy  y  7 2 2 2
2x 1  2x 1 2  4x  4x     7 0,25 x  x   
 4x  4x 2x   1  2x  2 1 4 2 2 2 2 4 2
1  7x  8x  7x 1  0   2 x   2 1 x   0    8  0,25 2
 x  1  x  1  .
Với x  1 y  1. 0,25
Với x  1 y  1
 . Vậy hệ phương trình có hai nghiệm  ;
x y  1;  1 ,1;  1 .
2b) Tìm tất cả các giá trị của m để hệ phương trình có nghiệm. 1,00
Ta có x  0 không thỏa mãn suy ra x  0.
Rút y từ PT thứ nhất rồi thế vào PT thứ hai ta có: 2 2 2 0,25
2x 1  2x 1 2 4x  4x     m x  x 
Hệ có nghiệm  x  x  x    x  2 4 2 2 2 2 4 4 2 1 2
1  mx có nghiệm khác 0. 0,25 4 2
 8x  mx 1  0 có nghiệm khác 0. Đặt 2
t  x ,t  0. Thay vào phương trình trên ta được 0,25 2
8t  mt 1  0 (1). Như vậy yêu cầu bài toán    1 có nghiệm dương.
Dễ thấy phương trình (1) luôn có 2 nghiệm trái dấu do ac  0 suy ra (1) luôn có một 0,25
nghiệm dương. Do đó với mọi số thực m hệ phương trình luôn có nghiệm.
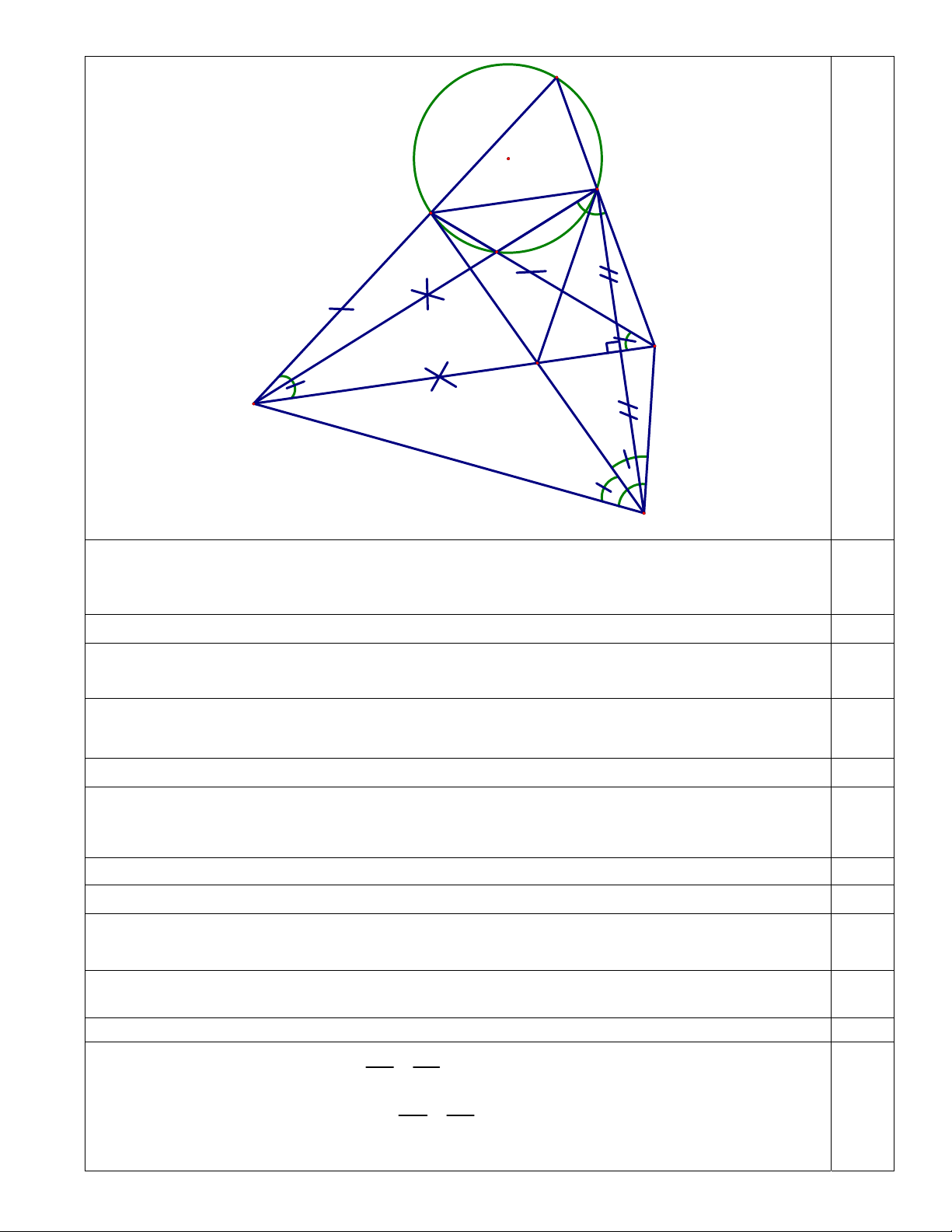
Câu 3 (3,0 điểm). Cho hình thang ABCD thỏa mãn AD, BC là hai đáy , BC  AD , BC  BD  1 ,
AB  AC , CD  1,   0
BAC  BDC  180 , E là điểm đối xứng với D qua đường thẳng BC.
a) Chứng minh rằng 4 điểm A, C, E, B cùng nằm trên một đường tròn và  
BEC  2.AEC .
b) Đường thẳng AB cắt đường thẳng CD tại điểm K , đường thẳng BC cắt đường thẳng
AE tại điểm F . Chứng minh rằng FA  FD và đường thẳng FD tiếp xúc với đường tròn
ngoại tiếp tam giác ADK .
c) Tính độ dài cạnh CD. Nội dung Điểm K D A L C F B E
3a) Chứng minh rằng 4 điểm A, C, E, B cùng nằm trên một đường tròn và  
BEC  2.AEC . 1,00
Do E đối xứng D qua BC nên   BDC  BEC 0,25 Có   0   0
BAC  BDC  180  BAC  BEC  180 suy ra ,
A C, E, B cùng nằm trên một đường 0,25 tròn.
Có tam giác ABC cân tại A nên  
ABC  ACB , kết hợp với tứ giác ACEB nội tiếp ta được     0,25
ABC  AEC, ACB  BEA . Từ đó suy ra  
AEC  BEA    BEC  2.AEC . 0,25
3b) Đường thẳng AB cắt đường thẳng CD tại điểm K , đường thẳng BC cắt đường
thẳng AE tại điểm F . Chứng minh rằng FA  FD và đường thẳng FD tiếp xúc với 1,00
đường tròn ngoại tiếp tam giác ADK .
Có: DE  BC, AD  BC  ADE 
vuông tại D và FD  FE  FA . 0,25 Mặt khác   0  
BAC  BDC  180  BAC  BDK  tứ giác AKDL nội tiếp. 0,25 Có  
ADB  DBC (do AD||BC), tứ giác ACEB nội tiếp suy ra  
CAE  CBE , do BC là trung 0,25 trực của BE nên  
DBC  CBE . Do đó  
ADB  CAE suy ra
FA là tiếp tuyến của đường tròn ngoại tiếp tam giác ADK, kết hợp với FA  FD  FD là 0,25
tiếp tuyến của đường tròn ngoại tiếp tam giác ADK.
3c) Tính độ dài cạnh CD. 1,00 FC CE
Do EF là phân giác  BEC , suy ra 
 CE (vì BE  BD 1) FB EB AC BE 0,25
Ta có AFC đồng dạng với BFE    AF BF
Áp dụng định lý Ptolemy có: AE.BC  A .
B CE  AC.BE  2AF  AC(1 CE) 0,25 2 AC BE BC BF  FC FC       1  1 CE 0,25 1 CE AF BF BF BF BF    EC2 1  2 1 EC  2 0.25
 CD  EC  2 1.
Câu 4 (2,0 điểm). Cho phương trình 2 2 2
x  y  z  3xyz (1). Mỗi bộ số  x, y, z trong đó x, y, z là
các số nguyên dương thỏa mãn (1) được gọi là một nghiệm nguyên dương của phương trình (1). Nội dung Điểm
4a) Tìm tất cả các nghiệm nguyên dương có dạng x, y, y của phương trình (1). 1,00
Giả sử phương trình có nghiệm nguyên dương là x, y, y . Khi đó thay vào phương trình 0,25 ta được: 2 2 2 2 2 2 2
x  y  y  3xy  x  2y  3xy . suy ra 2 2
x  y  x y  x  ty . Thay trở lại phương trình trên ta được 0,25 2 2 2 2 2
t y  2y  3t. .
y y  t  2  3ty .
Từ phương trình này ta được 2t  t 1,  2 . 0,25
Với t  1 y 1 x 1.
Với t  2  y 1 x  2. Do đó phương trình đã cho có hai nghiệm nguyên dương dạng 0,25
x, y, y là:1,1,  1 ,2,1,  1 .
4b) Chứng minh rằng tồn tại nghiệm nguyên dương a,b,c của phương trình (1) và
thỏa mãn điều kiện mina; ; b 
c  2017 . Trong đó kí hiệu min ; a ; b 
c là số nhỏ nhất 1,00
trong ba số a, b, . c
Ta có x  1, y  2, z  5 là một nghiệm của phương trình đã cho 0,25
Giả sử a  mina; ; b 
c với a  b  c thỏa mãn 2 2 2
a  b  c  3abc .
Xét phương trình: a  d 2 2 2
 b  c  a  d  2 3
bc  2ad  d  3bcd 0,25 *
 d  3bc  2a  N .
Suy ra phương trình (1) có nghiệm a '; ;
b c với a '  a  d .
Do a  b  c , suy ra mina '; ; b  c  mina; ; b  c  a . 0,25
Lặp lại quá trình trên sau không quá 2017 lần ta được mina; ; b  c  2017 . 0,25
Câu 5 (1,0 điểm). Cho số tự nhiên n  1 và số nguyên dương a , a ,..., a
thỏa mãn điều kiện 1 2 n2
1  a  a  ...  a
 3n . Chứng minh rằng luôn tồn tại hai số a , a (1 j  i  n  2;i, j  ) 1 2 n2 i j
sao cho n  a  a  2n . i j Nội dung Điểm
Với mọi k đặt b  a  k  a  a  a  k  a  k  b  b (2). Do đó ta có thể chọn k i i i j
 i   j  i j sao cho b
 3n và chuyển về xét dãy số 1 b  b  ...  b
 3n . Khi đó ta chỉ cần 0,25 n2 1 2 n2
chứng minh tồn tại hai số b , b (1  j  i  n  2;i, j  ) sao cho n  b  b  2n . i j i j Xét 2 trường hợp:
1. Nếu tồn tại j 1,2,...,n  
1 sao cho n  b  2n thì ta có: n  b  b  2n 0,25 j n2 j
2. Nếu với mọi j 1,2,...,n  
1 ta có b n 1; 2n   1 thì các số j
b , b ,..., b  1, 2,...,3n 1 \ n 1,..., 2n 1 . Các số thuộc tập 1 2 n 1      0,25 1,2,...,3n  
1 \ n 1,..., 2n  
1 chia thành n cặp số: 1; 2n, 2; 2n   1 ,...,  ; n 3n   1 . Do đó
trong n 1 số b , b ,..., b , tồn tại 2 số b , b ( j  i) thuộc cùng một cặp, chẳng hạn 1 2 n 1  i j
t; 2n t  
1 hay n  b  b  2n  t 1 t  2n 1  2n . Theo (2) từ cặp số b , b thỏa mãn i j i j 0,25
n  b  b  2n thì tồn tại cặp số a , a thỏa mãn n  a  a  2n . i j i j i j Lưu ý khi chấm bài:
- Hướng dẫn chấm (HDC) chỉ trình bày một cách giải bao gồm các ý bắt buộc phải có trong bài
làm của học sinh. Khi chấm nếu học sinh bỏ qua bước nào thì không cho điểm bước đó.
- Nếu học sinh giải cách khác, giám khảo căn cứ các ý trong đáp án để cho điểm.
- Trong bài làm, nếu ở một bước nào đó bị sai thì các phần sau có sử dụng kết quả sai đó không được điểm.
- Bài hình học nếu không vẽ hình phần nào thì không cho điểm phần đó.
- Điểm toàn bài tính đến 0,25 và không làm tròn. ---Hết---