Đề thi tuyển sinh lớp 10 THPT năm học 2017 – 2018 môn Toán sở GD và ĐT An Giang

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT AN GIANG Khóa ngày 07 – 7 ‐ 2017 ĐỀ THI CHÍNH THỨC Môn thi: TOÁN Đề thi gồm 01 trang
Thời gian: 120 phút không kể thời gian phát đề Câu 1. 3,0 điểm
Giải các phương trình và hệ phương trình sau đây: a √3 √12 √27 b 20 0 2 3 7 c 1 Câu 2. 1,5 điểm Cho hàm số có đồ thị là Parabol . a Vẽ đồ thị của hàm số đã cho.
b Tìm tọa độ giao điểm của và đường thẳng : 2 1 bằng phép tính. Câu 3. 1,5 điểm
Cho phương trình bậc hai ẩn : 4 1 8 0 là tham số .
a Chứng minh rằng phương trình luôn có hai nghiệm phân biệt , với mọi số .
b Tìm để hai nghiệm ; của phương trình đã cho thỏa điều kiện | | 17 Câu 4. 3,0 điểm
Cho điểm thuộc nửa đường tròn đường kính . Kẻ tiếp tuyến với nửa đường tròn đó
nằm trên cùng nửa mặt phẳng có bờ là đường thẳng
chứa nửa đường tròn . Tia phân giác của góc
cắt nửa đường tròn tại . Kéo dài và cắt nhau tại . Kẻ vuông góc với tại . a Chứng minh tứ giác nội tiếp. b Chứng minh . c Chứng minh tam giác cân. d Tia cắt và
lần lượt tại và . Chứng minh là hình thoi. Câu 5. 1,0 điểm
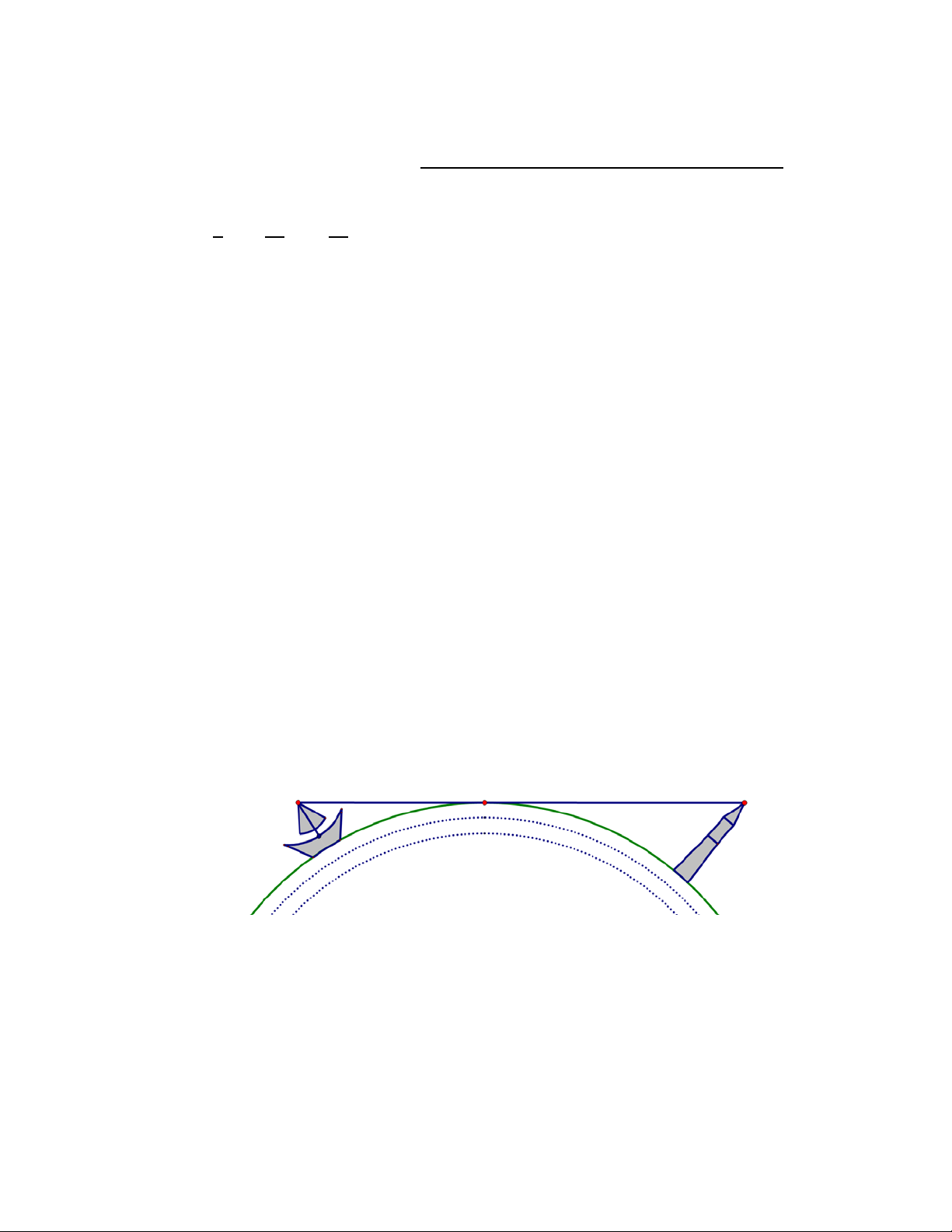
Ngọn Hải đăng Kê Gà ở tỉnh Bình Thuận là ngọn tháp thắp đèn gần bờ biển dùng để định
hướng cho tàu thuyền giao thông trong khu vực vào ban đêm. Đây là ngọn Hải đăng được xem
là cổ xưa và cao nhất Việt Nam, chiều cao của ngọn đèn so với mặt nước biển là 65 . Hỏi:
a Một người quan sát đứng tại vị trí đèn của Hải đăng nhìn xa tối đa bao nhiêu trên mặt biển?
b Cách bao xa thì một người quan sát đứng ở trên tàu bắt đầu trông thấy ngọn đèn
này, biết rằng mắt người quan sát đứng ở trên tàu có độ cao 5 so với mặt nước biển?
Cho biết bán kính Trái Đất gần bằng 6400
và điều kiện quan sát trên biển là không bị che khuất
‐‐‐‐‐ Hết ‐‐‐‐‐
HƯỚNG DẪN GIẢI CHI TIẾT
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT
Khóa ngày 07 – 7 – 2017 – An Giang
Gv giải đề: Nguyễn Chí Dũng
* Lưu ý: Lời giải chỉ mang tính chất tham khảo, không phải là đáp án chính thức. Câu 1. 3,0 điểm
Giải các phương trình và hệ phương trình sau đây: a √3 √12 √27 ⇔ √3 √12 √27 √27 ⇔ 1 √3 √12 Vậy 1 b 20 0 Ta có: 4 5 1 4. 5 20 Suy ra: 4; 5 Vậy 5; 4 2 3 7 c 1 2 3 7 5 10 2 ⇔ 3 3 3 ⇔ 3 3 3 ⇔ 1
Vậy hệ pt có nghiệm duy nhất 2; 1
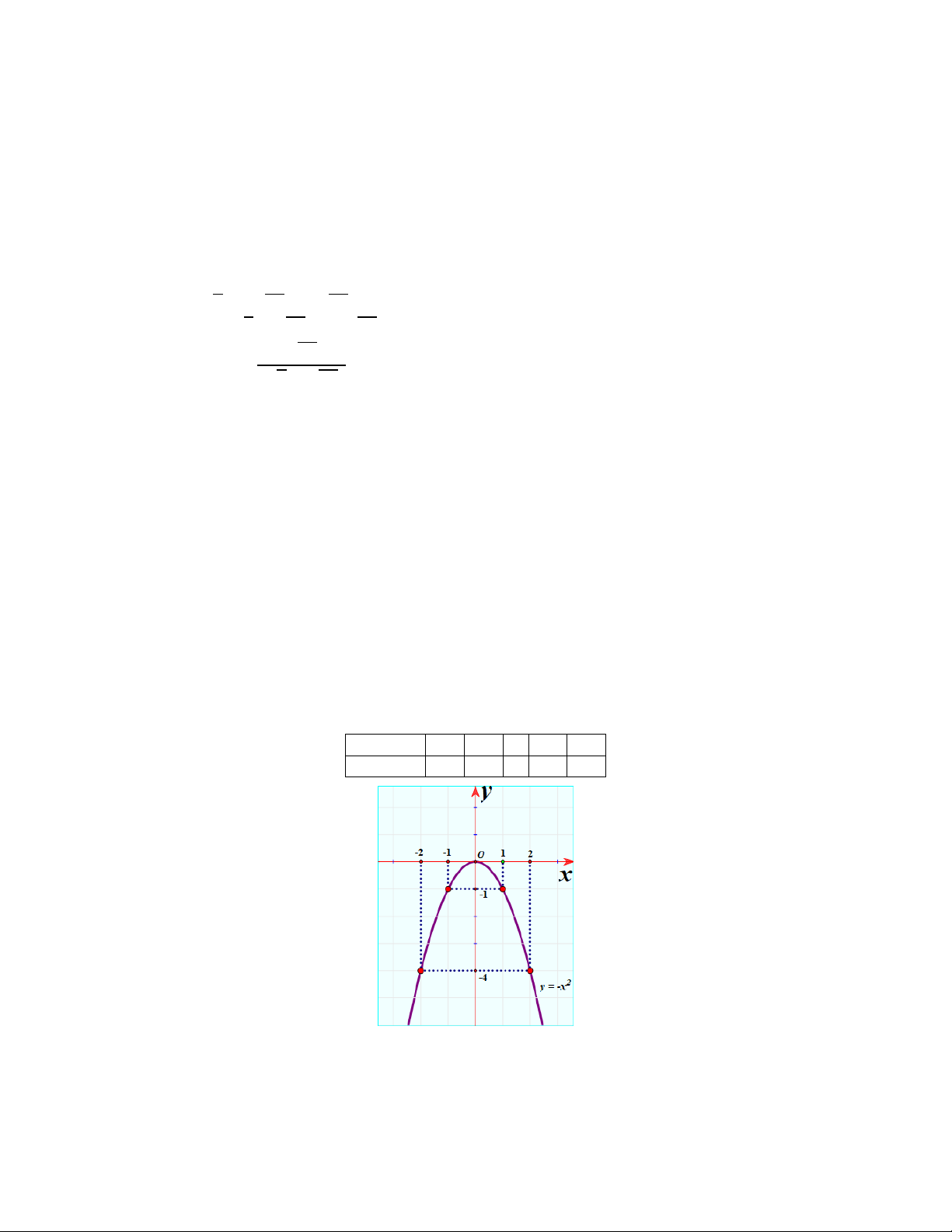
Câu 2. 1,5 điểm Cho hàm số có đồ thị là Parabol . a Vẽ đồ thị của hàm số đã cho. 2 1 0 1 2 4 1 0 1 4
b Tìm tọa độ giao điểm của và đường thẳng : 2 1 bằng phép tính. Pt hoành độ giao điểm: 2 1 ⇔ 2 1 0 ⇔ 1 0 ⇔ 1 Suy ra: 1
Vậy 1; 1 là tọa độ giao điểm cần tìm. Câu 3. 1,5 điểm
Cho phương trình bậc hai ẩn : 4 1 8 0 là tham số .
a Chứng minh rằng phương trình luôn có hai nghiệm phân biệt ; với mọi số . Do .
0 nên pt luôn có hai nghiệm phân biệt với mọi số
b Tìm để hai nghiệm ; của phương trình đã cho thỏa điều kiện | | 17 Theo Vi‐ét, ta có: 4 1 ; . 8 Theo đề bài, ta có: | | 17 ⇔ 4 17 4 1 4. 8 17 ⇔ 16 8 1 32 17 ⇔ 16 8 256 0 1 √257 ⇔ 4 Câu 4. 3,0 điểm
Cho điểm thuộc nửa đường tròn đường kính . Kẻ tiếp tuyến với nửa đường tròn đó
nằm trên cùng nửa mặt phẳng có bờ là đường thẳng
chứa nửa đường tròn . Tia phân giác của góc
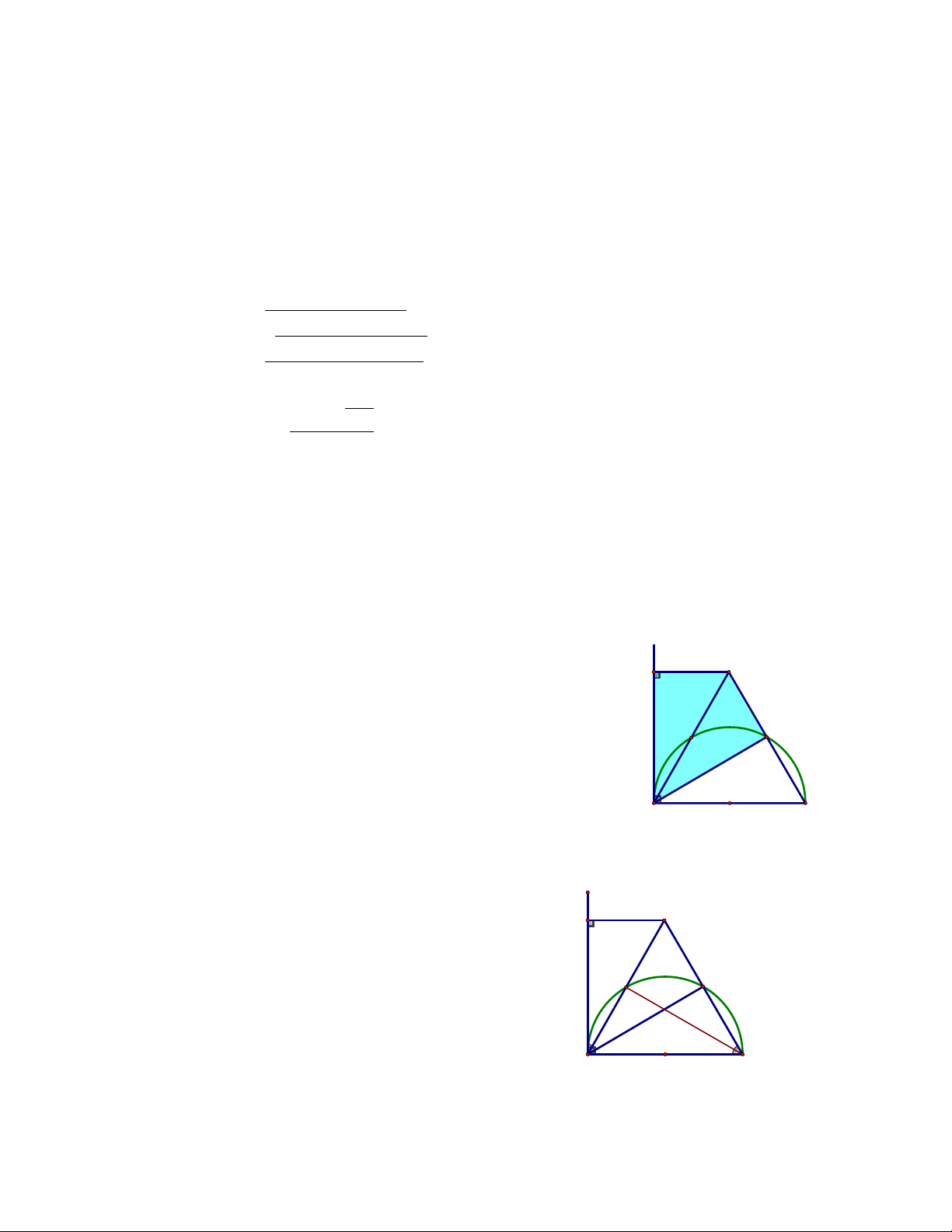
cắt nửa đường tròn tại . Kéo dài và cắt nhau tại . Kẻ vuông góc với tại . a Chứng minh tứ giác nội tiếp. x E H Xét tứ giác ta có: 90 do tại
90 kề bù với góc nội tiếp chắn nửa đường tròn D C Suy ra: 90 90 180
Mà , là hai đỉnh đối nhau nên nội tiếp. b Chứng minh . A B cùng chắn cung cùng chắn cung Mà nên x E H c Chứng minh tam giác cân. D C 90 90 Mà nên Vậy tam giác cân tại B A B d Tia cắt và
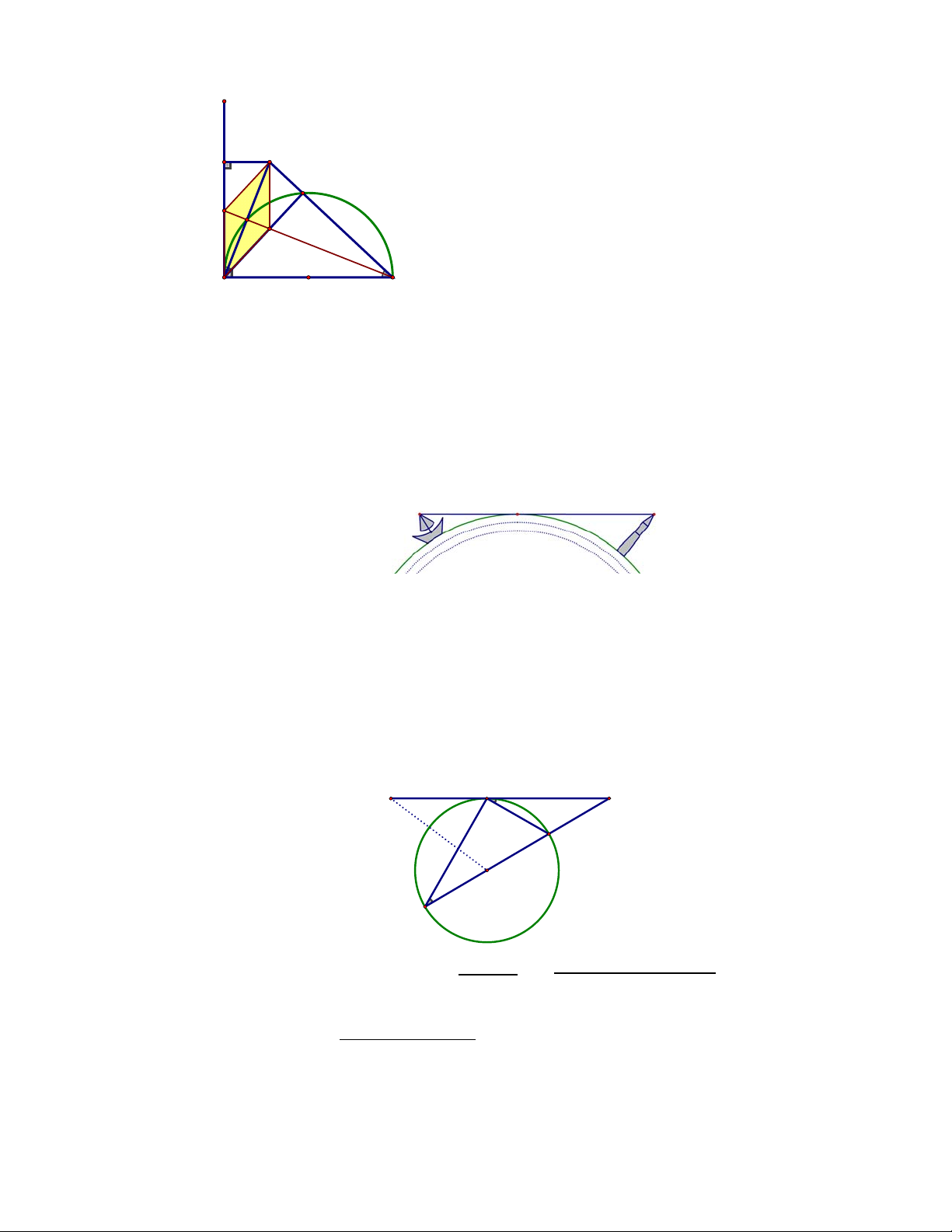
lần lượt tại và . Chứng minh là hình thoi. x E H C D K F A B ∆ có
là phân giác, là đường cao nên ∆ cân tại Suy ra: là trung tuyến
Do đó: là trung điểm của * ∆ cân tại và có là đường cao nên là trung tuyến
Do đó: là trung điểm của ** Từ * và ** suy ra: là hình bình hành Mặt khác,
là phân giác của góc nên là hình thoi. Câu 5. 1,0 điểm
Ngọn Hải đăng Kê Gà ở tỉnh Bình Thuận là ngọn tháp thắp đèn gần bờ biển dùng để định
hướng cho tàu thuyền giao thông trong khu vực vào ban đêm. Đây là ngọn Hải đăng được xem
là cổ xưa và cao nhất Việt Nam, chiều cao của ngọn đèn so với mặt nước biển là 65 . Hỏi:
c Một người quan sát đứng tại vị trí đèn của Hải đăng nhìn xa tối đa bao nhiêu trên mặt biển?
d Cách bao xa thì một người quan sát đứng ở trên tàu bắt đầu trông thấy ngọn đèn
này, biết rằng mắt người quan sát đứng ở trên tàu có độ cao 5 so với mặt nước biển?
Cho biết bán kính Trái Đất gần bằng 6400
và điều kiện quan sát trên biển là không bị che khuất T N M A O B a ∆ ∽ ∆ (g-g) Suy ra: . ⇒ √ . 65. 65 2.6400000 29
Vậy một người quan sát đứng tại vị trí đèn của Hải đăng nhìn xa tối đa khoảng 29 có thể thấp hơn 29 b Tương tự, 5 5 2.6400000 8 Suy ra: 29 8 37 có thể thấp hơn 37 Vậy cách bao xa khoảng 37
thì một người quan sát đứng ở trên tàu bắt đầu trông thấy ngọn đèn này.
‐‐‐‐‐ Hết ‐‐‐‐‐