Đề thi tuyển sinh lớp 10 THPT năm học 2017 – 2018 môn Toán sở GD và ĐT Phú Thọ

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH PHÚ THỌ
VÀO LỚP 10 TRUNG HỌC PHỔ THÔNG
NĂM HỌC 2017 – 2018 ĐỀ CHÍNH THỨC Môn: TOÁN
Thời gian làm bài: 120 phút, không kể thời gian giao đề
Đề thi có 01 trang
Câu 1 (1,5 điểm) x 1 a) Giải phương trı̀nh: 1  0 . 2
2x  y  3
b) Giải hệ phương trình:  . 2 x  y  5
Câu 2 (2,5 điểm) 1
Trong mặt phẳng tọa độ Oxy cho parabol (P) có phương trình 2
y  x và hai điểm A, 2
B thuộc (P) có hoành độ lần lượt là x  1; x  2 . A B a) Tìm tọa độ A, B.
b) Viết phương trình đường thẳng (d) đi qua hai điểm A,B.
c) Tính khoảng cách từ O (gốc tọa độ) đến đường thẳng (d).
Câu 3 (2,0 điểm) Cho phương trình: 2 2
x  2(m 1)x  m  m 1  0 (m là tham số).
a) Giải phương trình với m  0 .
b) Tìm m để phương trình có hai nghiệm phân biệt x , x thỏa mãn điều kiện : 1 2 1 1   4 . x x 1 2
Câu 4 (3,0 điểm)
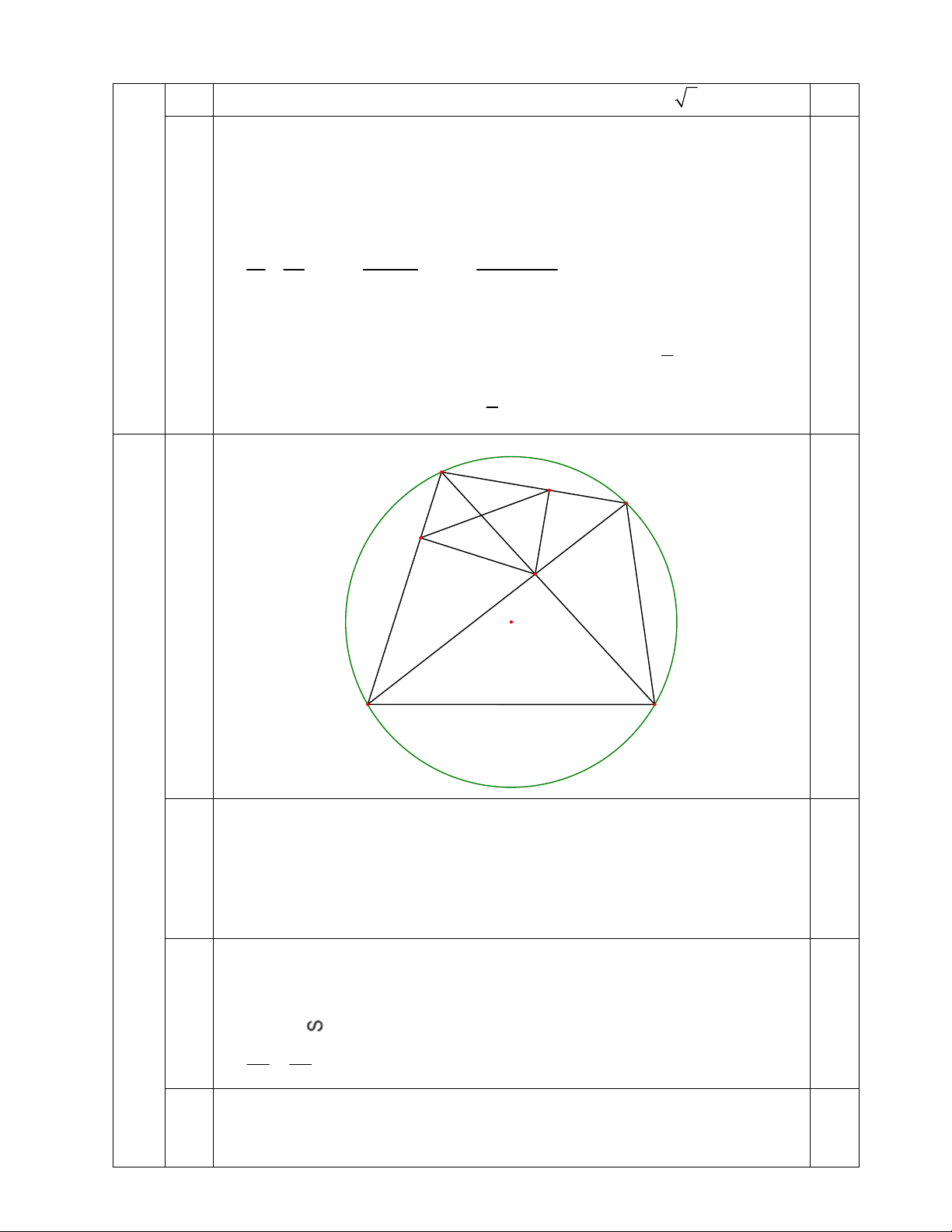
Cho tứ giác ABCD nội tiếp đường tròn (O; R). Gọi I là giao điểm AC và BD. Kẻ IH vuông
góc với AB; IK vuông góc với AD ( H  ; AB K  AD ).
a) Chứng minh tứ giác AHIK nội tiếp đường tròn.
b) Chứng minh rằng IA.IC = IB.ID.
c) Chứng minh rằng tam giác HIK và tam giác BCD đồng dạng.
d) Gọi S là diện tích tam giác ABD, S’ là diện tích tam giác HIK. Chứng minh rằng: 2 S ' HK  2 S 4.AI
Câu 5 (1,0 điểm)
Giải phương trình : x     3 4 (x  4)  42 3 3 2 2 .
-------------- Hết--------------
Họ và tên thí sinh: ...................................................................... SBD: .................
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
HƯỚNG DẪN GIẢI VÀ BIỂU ĐIỂM DỰ KIẾN: Phầ Điể Câu Nội dung n m x 1 x 1 1  0 
 1  x 1  2  x  1 a) 2 2 0.75
Vậy nghiệm của phương trình là x = 1. 2 2 2x  y  3 x  2x  2 x  2x  2  0 (1)      2 x  y  5 2x  y  3 y  3  2x (2) Câu 1
Giải (1):  '  3 ; x  1 3 1,2 (1,5 Thay vào (2): đ)
b) Với x 1 3 thì y  3  21 3 1 2 3 0.75
Với x  1 3 thì y  3  21 3 1 2 3
Vậy nghiệm của hệ phương trình là:
x,y 1 3;12 3,1 3;1 2 3. Vì A, B thuộc (P) nên: 1 2 1 x  1   y  ( 1  )  A A 2 2 a) 1 2 x  2  y   2  2 0.75 B B 2  1  Vậy A 1  ; , B(2;2)   .  2 
Gọi phương trình đường thẳng (d) là y = ax + b. Ta có hệ phương trình: Câu  1  3  1 a  b  3  a  a  2 b)  2   2   2 0.75 (2,5 2a  b  2
2a  b  2 b 1 đ) 1 Vậy (d): y  x 1. 2
(d) cắt trục Oy tại điểm C(0; 1) và cắt trục Ox tại điểm D(– 2; 0)  OC = 1 và OD = 2
Gọi h là khoảng cách từ O tới (d).
Áp dụng hệ thức về cạnh và đường cao vào  vuông OCD, ta có: c) 1 1 1 1 1 5 1.0      2 2 2 2 2 h OC OD 1 2 4 2 5  h  5 2 2 Câu
x  2(m 1)x  m  m 1  0 (1) 3
a) Với m = 0, phương trình (1) trở thành: 2 x  2x 1  0 1.0 (2,0  '  2 ; x  1 2 1,2 đ)
Vậy với m = 2 thì nghiệm của phương trình (1) là x  1 2 . 1,2  '  m  2
Phương trình (1) có hai nghiệm phân biệt  m  2 x  x  2(m 1)
Áp dụng hệ thức Vi-ét, ta có: 1 2  2 x x  m  m 1  1 2 Do đó: 1 1 x  x 2(m 1) 1 2 b)   4   4   4 2 x x x x m  m 1 1.0 1 2 1 2   2 2 m 1 m  m 1  0 m  m 1  0       3 2 2
m 1  2(m  m 1) 2m  m  3  0 m    2  3 
Kết hợp với điều kiện  m  1
 ;  là các giá trị cần tìm.  2  A H 1 B 1 1 K 1 I 0.25 O 1 D C Câu 4 (3,0 Tứ giác AHIK có: đ)  0 AHI  90 (IH  AB) a)  0 AKI  90 (IK  AD) 0.75   0  AHI  AKI  180
 Tứ giác AHIK nội tiếp.  IAD và  IBC có:   1 A  1
B (2 góc nội tiếp cùng chắn cung DC của (O))   b)
AID  BIC (2 góc đối đỉnh) 0.5   IAD  IBC (g.g) IA ID    IA.IC  IB.ID IB IC
Xét đường tròn ngoại tiếp tứ giác AHIK có c)   1 A  1
H (2 góc nội tiếp cùng chắn cung IK) 0.75 Mà     1 A  1 B  1 H  1 B
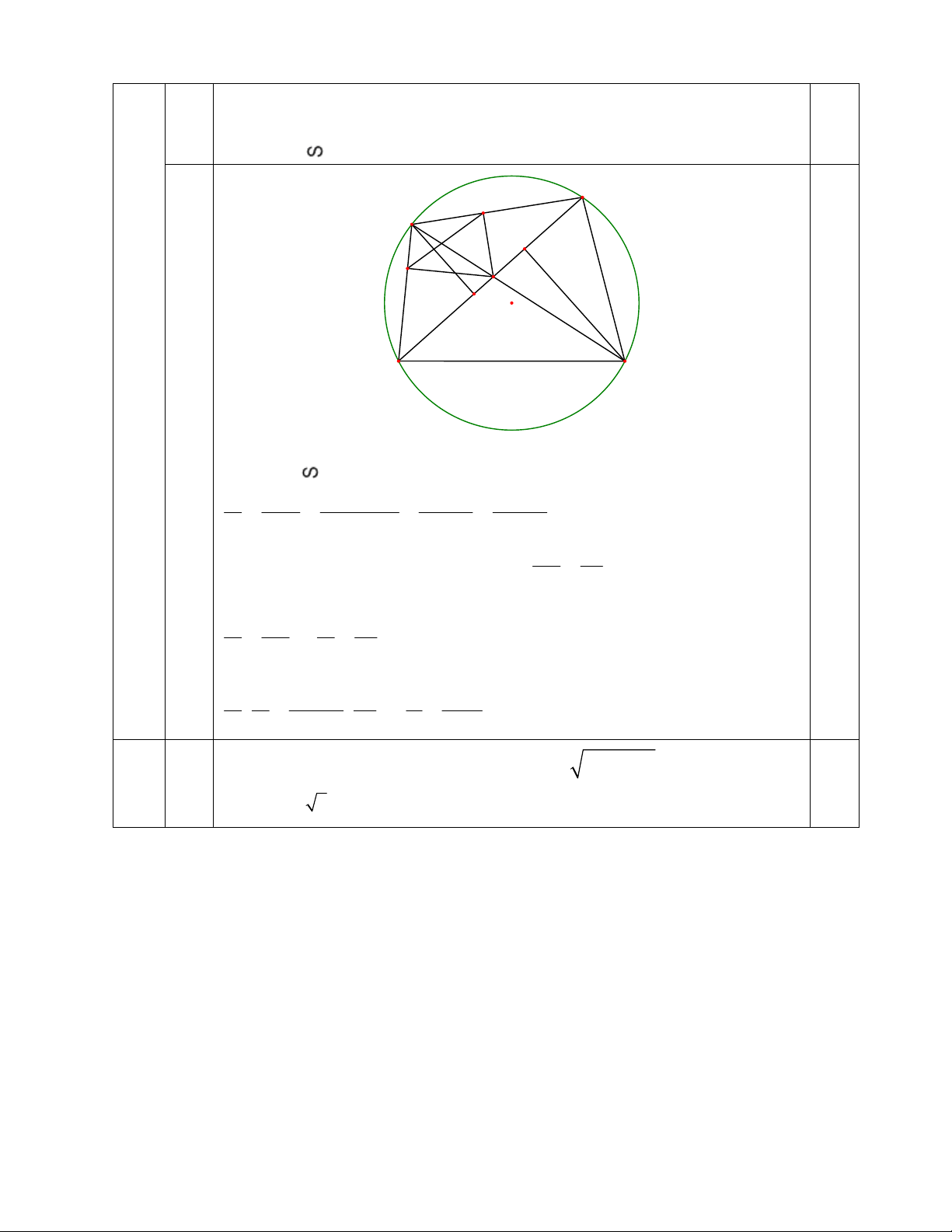
Chứng minh tương tự, ta được   K1  1 D  HIK và  BCD có:     1 H  1 B ; K1  1 D   HIK  BCD (g.g) B H A I F K E O D C
d) Gọi S1 là diện tích của  BCD. 0.75 Vì  HIK  BCD nên: 2 2 2 2 S' HK HK HK HK     (1) 2 2 S BD (IB  ID) 4IB.ID 4IA.IC 1 CF IC
Vẽ AE  BD , CF  BD  AE / /CF   AE IA
 ABD và  BCD có chung cạnh đáy BD nên: S CF S IC 1 1    (2) S AE S IA Từ (1) và (2) suy ra 2 2 S' S HK IC S' HK 1      (đpcm) 2 S S 4IA.IC IA S 4IA 1 Câu 5
Câu 5 (1 điểm) Giải phương trình  x     x   2 3 3 2 2 3 4 ( 4) 4 1.0 (1,0 ĐKXĐ 3 x  4 đ)
x 4 3 (x 4) 42 x 4 x  3 (x 4) 42 3 3 3
 x  42  x  42 3 2 2 3 2 2 2 2 2
x 4 x x 42 3 2 3 2 x  3 x 4 4 x            3 2 2 2
(x  4)  4  x  4 3 2 2 2
(x  4)  x  4   
x 4 x x 42 3 2 3 2 x  3 x 4 4 x             3 2 2 2
(x  4)  x  3 2 2 2
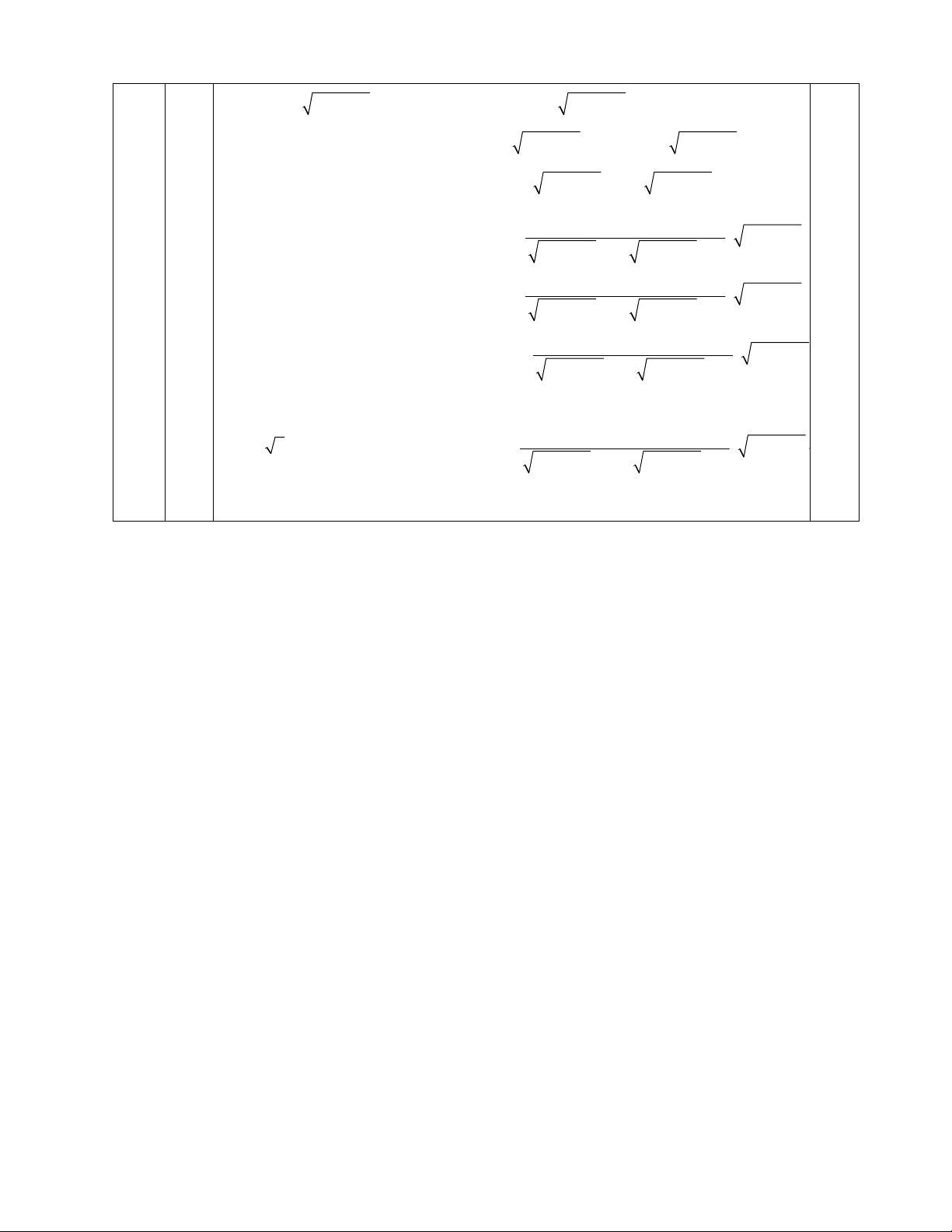
(x  4)  x  4   2x 2 2 6 x  4  x 3   2 x  2 4 x  3 x 4 2 x  3 x 4 4   x        (x  4)    3 2 4 2 3 2 2 4  3 2 2 (x  4)  x (x  4)  x 2 3 2 3  x   x x   x x
4 x x 42 4 4 3 2 3 2 x  3 x 4 4    x          (x  4)    3 2 4 2 3 2 2 4  3 2 2 (x  4)  x (x  4)  x   2 3 x  4  x  4 
 x  4  x  x  42 3 2 3 2  x  3
x  4  x  (x  4)   3 2 4 2 3 2 2 4  3 2 2  (x  4)  x (x  4)  x  3 2
 x  4  x  0  x  2 2
x  x  2  0  x  2 2 3  x  4  x  3 Vi x 4 thi    x 42 3 2 x  3 x 4 4   x        (x  4)    3 2 4 2 3 2 2 6  3 2 2 
(x  4)  x (x  4)  x 