Đề thi tuyển sinh lớp 10 THPT năm học 2017 – 2018 môn Toán sở GD và ĐT TP. HCM

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 TRUNG HỌC PHỔ THÔNG THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC 2017 – 2018 MÔN THI: TOÁN
Ngày thi: 03 tháng 6 năm 2017 ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút (không kể thời gian phát đề)
(Đề thi gồm 01 trang) Câu 1. (2 điểm) a) Giải phương trình: 2
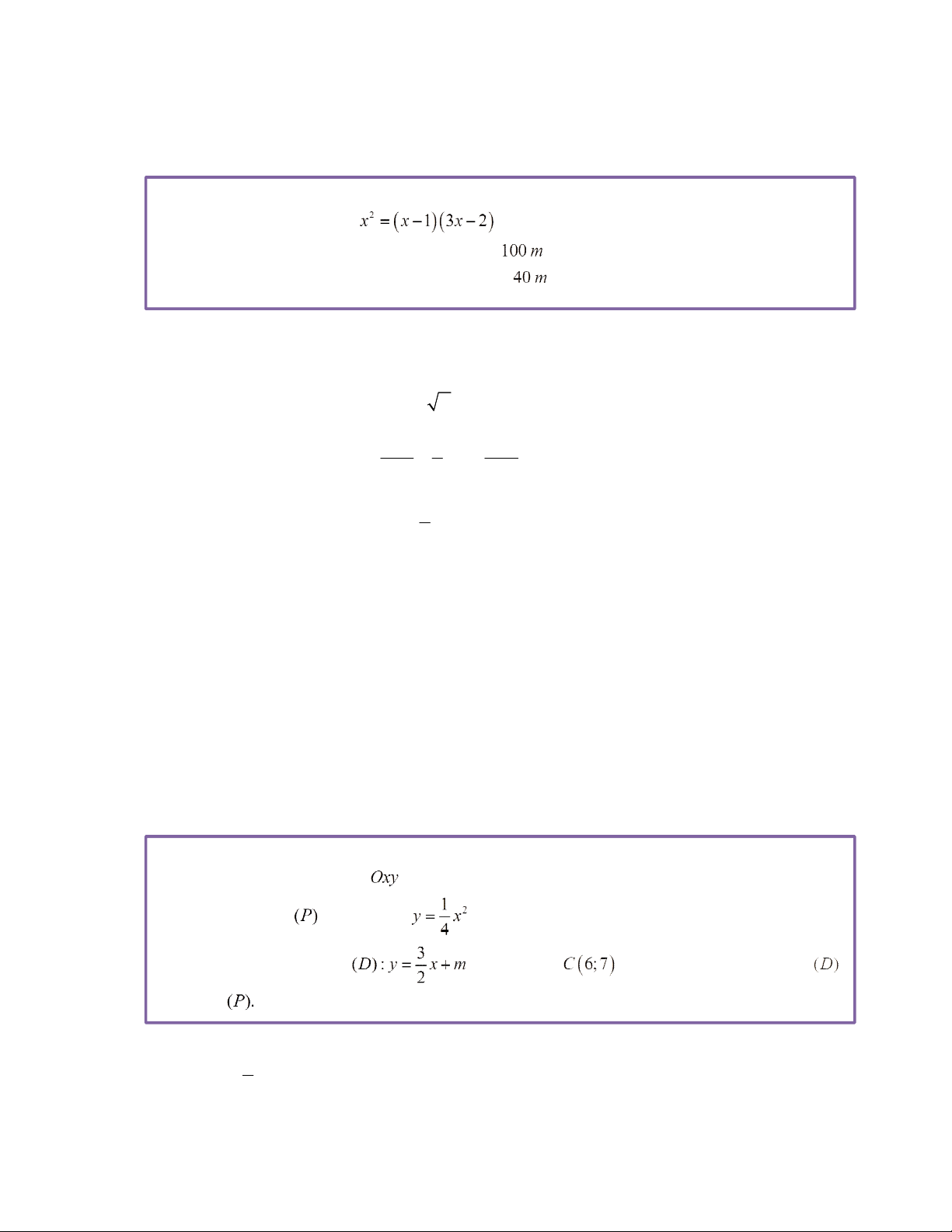
x   x   1 3x  2
b) Một miếng đất hình chữ nhật có chu vi 100 m . Tính chiều dài và chiều rộng của miếng đất,
biết rằng 5 lần chiều rộng hơn 2 lần chiều dài 40 m . Câu 2. (1,5 điểm)
Tròn mặt phẳng tọa độ Oxy : 1
a) Vẽ đồ thị (P) của hàm số 2 y  x . 4 3
b) Cho đường thẳng (D) : y 
x  m đi qua điểm C 6;7 . Tìm tọa độ giao điểm của (D) và 2 (P). Câu 3. (1,5 điểm) 
1) Thu gọn biểu thức sau: A     14 6 3 3 1 5  3
2) Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B) phải leo lên và
xuống một con dốc (như hình vẽ bên dưới). Cho biết đoạn thẳng AB dài 762 m , góc 0 A  6 , góc 0 B  4 .
a) Tính chiều cao h của con dốc.
b) Hỏi bạn an đến trường lúc mấy giờ? Biết rằng tốc độ trung bình lên dốc là 4 km/h và tốc
độ trung bình xuống dốc là 19 km/h. Câu 4: (1,5 điểm) Cho phương trình: 2
x   m   2 2
1 x  m 1  0 (1) ( x là ẩn số)
a) Tìm điều kiện của m để phương trình (1) có 2 nghiệm phân biệt.
b) Định m để hai nghiệm x , x của phương trình (1) thỏa mãn: 1 2
 x  x 2  x  3x 1 2 1 2 Câu 5. (3,5 điểm)
Cho tam giác ABC vuông tại A . Đường tròn tâm O đường kính AB cắt các đoạn BC và OC
lần lượt là D và I . Gọi H là hình chiếu của A lên OC ; AH cắt BC tại M .
a) Chứng minh: Tứ giác ACHD nội tiếp và   CHD  ABC.
b) Chứng minh: Hai tam giác OHB và OBC đồng dạng với nhau và HM là tia phân giác của góc . BHD c)) ọ
G i K là trung điểm của BD. Chứng minh: MD.BC  MC.CD và MB.MD  MK.MC.
d)) Gọi E là giao điểm của AM và OK ; J là giao điểm của IM và O (J khác I).
Chứng minh: Hai đường thẳng OC và EJ cắt nhau tại một điểm nằm trên O . HƯỚNG DẪN CHI TIẾT Câu 1. (2 điểm) a) Giải phương trình:
b) Một miếng đất hình chữ nhật có chu vi
. Tính chiều dài và chiều rộng của miếng
đất, biết rằng 5 lần chiều rộng hơn 2 lần chiều dài . Hướng dẫn giải. a. Ta có 2 2 2 2
x  (x 1)(3x  2)  x  3x  2x  3x  2  2x  5x  2  0 . Tính 2
  (5)  4.2.2  25 16  9  0,   3. 5  3 1 5  3
Phương trình có hai nghiệm x   , x   2 . 1 2 2.2 2 2.2  1 
Tập nghiệm của phương trình: S  2;   2 
b. Gọi x, y (m) là chiều dài và chiều rộng của miếng đất.
Nửa chu vi 100 : 2  50 (m).
Khi đó: x  y  50
Và 5y  2x  40  2x  5y  4
 0 . Ta có hệ phương trình
x  y  50  2
 x  2 y  100 
x  y  50
x  50  y x  30         
2x  5 y  40 
2x  5 y  40 7  y  140  y  20 y  20     
Vậy chiều dài của mảnh đất là 30 (m) và chiều rộng là 20 (m). Câu 2. (1,5 điểm)
Tròn mặt phẳng tọa độ : a) Vẽ đồ thị của hàm số . b) Cho đường thẳng đi qua điểm
. Tìm tọa độ giao điểm của và Hướng dẫn giải. 1 a. Đồ thị 2 y  x . 4
Tập xác định D   . Bảng giá trị x 2  1  0 1 2 1 1 y 1 0 1 4 4 Đồ thị 3 3
b. Đường thẳng (D) : y 
x  m qua C(6;7) nên ta có 7 
.6  m  m  2  . Vậy đường thẳng 2 2 3 ( )
D có phương trình y  x  2 . 2
Phương trình hoành độ giao điểm (D) và (P) : 1 3 1 3 2 2 2 x  x  2  x 
x  2  0  x  6x  8  0 4 2 4 2 Ta có 2  '  ( 3
 )  8  1  0 . Phương trình có hai nghiệm x  3 1  4, x  3 1  2 . 1 2 3 3 3 3 Khi đó y  x  2  .4  2  4 , y  x  2  .2  2  1 . 1 1 2 2 1 1 2 2
Tọa độ giao điểm (D) và (P) là A4; 4 và B 2  ;1 Câu 3. (1,5 điểm)
1) Thu gọn biểu thức sau:
2) Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B) phải leo lên và
xuống một con dốc (như hình vẽ bên dưới). Cho biết đoạn thẳng AB dài , góc , góc
a) Tính chiều cao của con dốc.
b) Hỏi bạn an đến trường lúc mấy giờ? Biết rằng tốc độ trung bình lên dốc là km/h và
tốc độ trung bình xuống dốc là km/h. Hướng dẫn giải.  1) Vì A     14 6 3 3 1 nên A  0 5  3 Ta có: 4 2  3 7  2 3 14  6 3 2 2   
 A  4  2 3  A  5  3 5  3 4 5  3 2   2  A   A  4 5  3  A  2 2)
a) Xét tam giác ABC có đường cao CH. CH CH Ta có: AH  ; BH  0 0 tan 6 tan 4 CH CH  1 1 
Mà AH  BH  762  
 762  CH  762 :   32. 0 0  0 0  tan 6 tan 4  tan 6 tan 4 
b) Xét tam giác ABC có đường cao CH. Ta có: CH CH 32 0 sin 6   AC    306. 0 0 AC sin 6 sin 6 CH CH 32 0 sin 4   BC    459. 0 0 BC sin 4 sin 4
Thời gian di chuyển từ A đến B: S AC 306
- Thời gian đi từ A đến C: t     0, 0765 giờ AC v 4 4.1000 S CB 459
- Thời gian di chuyển từ C đến B: t     0, 024 giờ CB v 19 19.1000
- Thời gian di chuyển từ A đến B: t
 0,0765  0, 024  0,1005 giờ  6 phút AB
Vậy bạn An đến trường lúc 6 giờ 6 phút. Câu 4: (1,5 điểm) Cho phương trình: ( là ẩn số) a) Tìm điều kiện của
để phương trình (1) có 2 nghiệm phân biệt. b) Định để hai nghiệm
của phương trình (1) thỏa mãn: Hướng dẫn giải. Phương trình 2 2
x  (2m 1)x  m 1  0 (1).
a. Ta có a  1  0 và 2 2
  (2m 1)  4(m 1)  4
 m  5 . Phương trình có hai nghiệm phân biệt khi 5
  0  4m  5  0  m  . 4 5
b. Theo Câu a, với điều kiện m 
, phương trình (1) có hai nghiệm x , x , theo định lý Viet ta có: 4 1 2
x  x  2m 1 1 2  và 2 2 2 2
(x  x )  (x  x )  4x x  (2m 1)  4(m 1)  4m  5 . Theo đề bài 2 1 2 1 2 1 2 x x  m 1  1 2 2
(x  x )  x  3x  x  3x  4m  5 . 1 2 1 2 1 2 Ta có:
x  2m 1 x 1 2
x  x  2m 1
x  x  2m 1 1 2 1 2       3m  3
x  3x  4m  5 4x  6m  6 x   1 2  2  2  2  3m  3  m 1 x  2m 1 x  1 1  2    2     3m  3 3m  3   x  x  2 2   2   2 Khi đó m 1 3(m 1) 2 2 2 2
x x  m 1  .
 m 1  3(m 1)  4(m 1) 1 2 2 2 2
 m 1  0  m  1 m  1 
Vậy m  1 m  1
 thỏa yêu cầu bài toán. Câu 5. (3,5 điểm) Cho tam giác vuông tại . Đường tròn tâm đường kính cắt các đoạn và lần lượt là và . Gọi là hình chiếu của lên ; cắt tại a) Chứng minh: Tứ giác nội tiếp và b) Chứng minh: Hai tam giác và
đồng dạng với nhau và HM là tia phân giác của góc
c) Gọi K là trung điểm của BD. Chứng minh: và d) Gọi là giao điểm của và ; . .là giao điểm của và (J khác I).
Chứng minh: Hai đường thẳng và
cắt nhau tại một điểm nằm trên . Hướng dẫn giải. a. Ta có:   0
AHC  ADC  90  ACDH nội tiếp. Ta có:  
CHD  CAD (do ACDH nội tiếp) Mà:   CAD  CBA Suy ra:   CHD  ABC OH OB b. Ta có: 2 2
OH.OC  OA  OB   OB OC
Suy ra: OHB ∽ OBC c g c        OHB  ABC Mà:   CHD ABC cmt      OHB  DHC Mặt khác:   0   0
OHB  BHM  90 ; DHC  DHM  90 Suy ra:  
BHM  DHM  HM là tia phân giác của góc BHD . MD HD
c. Ta có: HM là tia phân giác trong của BHD   MB HB CD HD
Mà: HC  HM  HC là tia phân giác ngoài của BHD   CB HB CD MD Suy ra: BHD    . MD BC  . MB CD CB MB OH OE Ta có: 2 2
OHE ∽ OKC  
 OH.OC  OK.OE  OB  OD OK OC    0
OBK ∽ OEB  OBE  OKB  90 Suy ra:    0
ODK ∽ OED  ODE  OKD  90 
Ta có: 5 điểm O, H , D, E, B cùng thuộc đường tròn đường kính OE  DHBE nội tiếp
 MD.MB  MH .ME
Ta có: tứ giác CHKE nội tiếp  MH .ME  MK.MC Suy ra:  .
MD MB  MK.MC
d. Gọi F là giao điểm của EJ với đường tròn.
Ta có: EB là tiếp tuyến của đường tròn O 2
 EB  EJ.EF  EK.EO  EM .EH
Theo phương tích đảo  FHMJ nội tiếp  0
 MJF  90  IF là đường kính  đpcm ------HẾT------