HƯỚNG DẪN GIẢI VÀ BIỂU ĐIỂM DỰ KIẾN:
I. TRẮC NGHIỆM (2 điểm). Câu 1 2 3 4 Đáp án D A B D
II. TỰ LUẬN (8 điểm). Câu Phần Nội dung Điểm
Với m = 2, hệ (1) trở thành: x  2y  1 x  2y  1 5  x  25      2x  y  12 4x  2y  24 2x  y  12 a) 0.75 x  5 x  5     2.5  y  12 y  2
Vậy với m = 2 thì nghiệm của hệ (1) là (5; 2). 1 2  Ta thấy:  b) 2 1 0.25
 Hệ (1) luôn có nghiệm duy nhất với mọi m. Câu x  2y  3  m 2x  4y  6  2m x  2y  3  m      5 2x  y  3(m  2) 2x  y  3m  6 5  y  5m (2,0đ) x  2m  3  m x  m  3     y  m y  m Do đó: c)
A = x2 + y2 = (m + 3)2 + m2 = 2m2 + 6m + 9 1.0 2  3  9 9  2 m    m     2  2 2 3
Dấu “=” xảy ra  m   2 9 3 Vậy min A   m   2 2
Gọi số hàng ghế lúc đầu là x ( * x  N ; x  2;80x ).  80
Số ghế ở mỗi hàng lúc đầu là (chiếc). x
Nếu bớt đi 2 hàng thì số hàng còn lại là x – 2. Câu 80
Khi đó, số ghế ở mỗi hàng là (chiếc). 6 a) x  2 1.0 (2,0đ)
Vì lúc đó mỗi hàng còn lại phải xếp thêm 2 ghế nên ta có phương trình: 80 80   2 x  2 x
Giải phương trình được: x1 = 10 (thỏa mãn điều kiện)
x2 = – 8 (không thỏa mãn điều kiện)
Vậy lúc đầu có 10 hàng ghế.
Xét phương trình hoành độ giao điểm của (P) và (d): 2 2
x  x  2  x  x  2  0
Vì a + b + c = 1 + 1 – 2 = 0 nên phương trình có hai nghiệm: x1 = 1; x2 = – 2
Với x = 1 thì y = 1 – 2 = – 1
Với x = – 2 thì y = – 2 – 2 = – 4
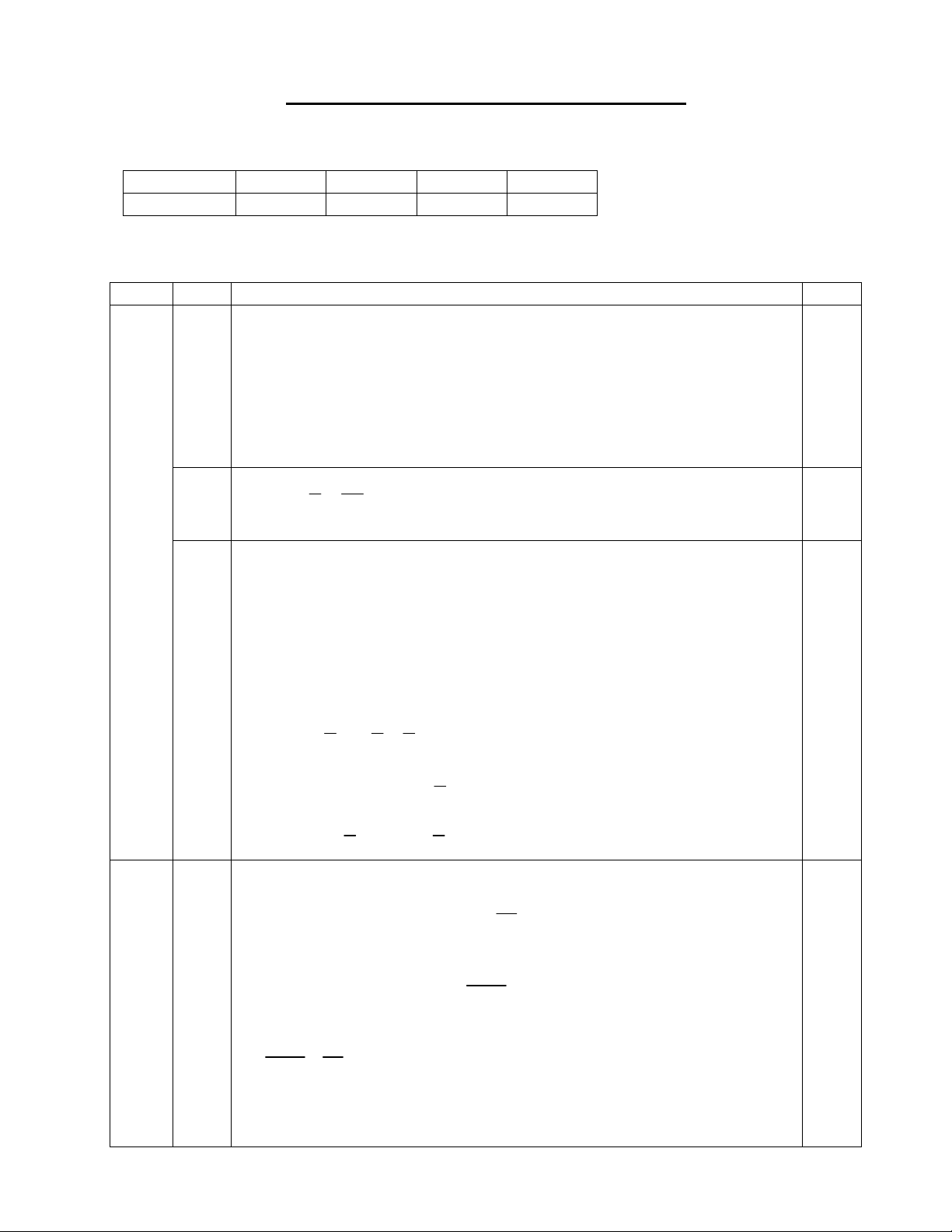
 A(1; – 1) và B(– 2; – 4) y O b) -3 -2 -1 1 2 3 x 1.0 -1 A 2 C B 4
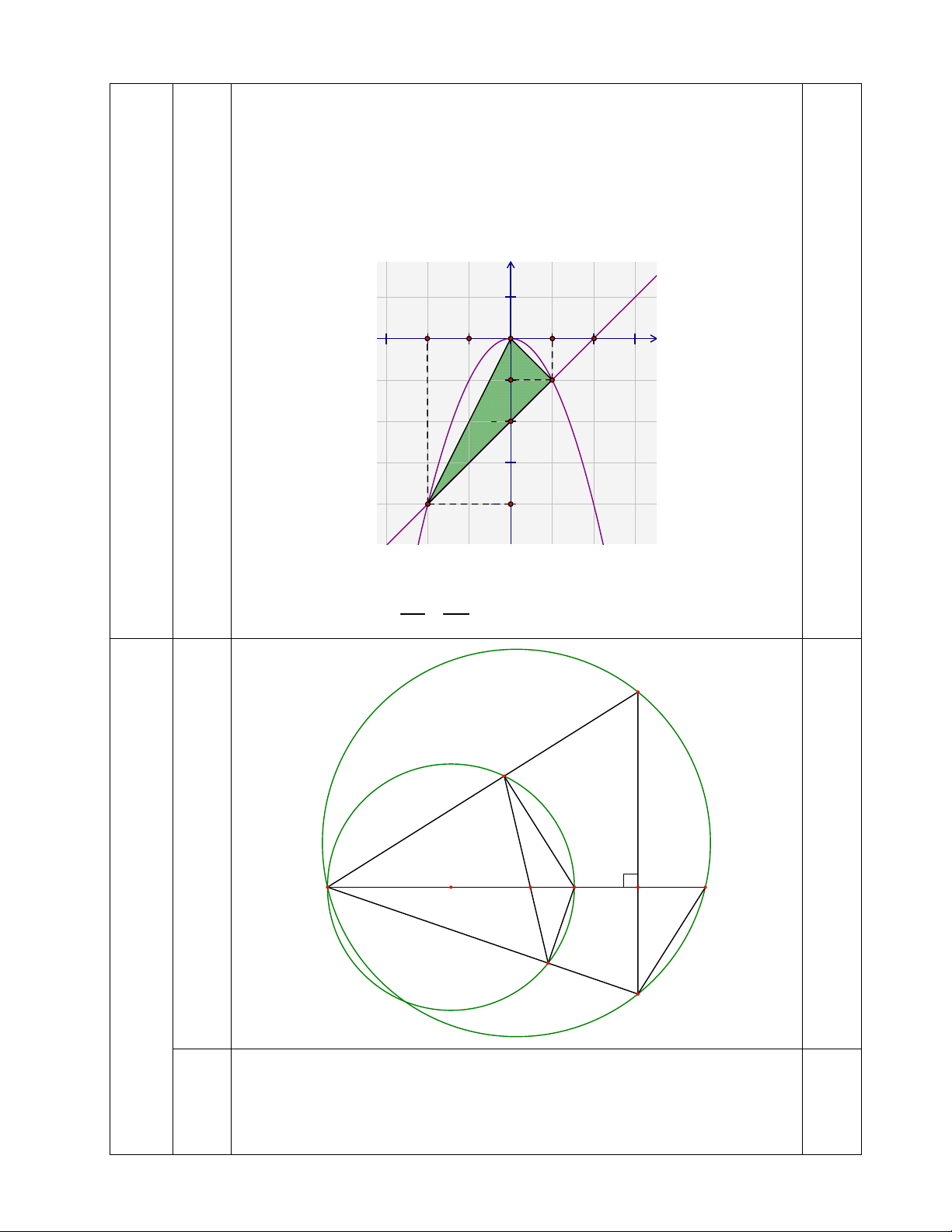
Dễ thấy (d) cắt Oy tại điểm C(0; – 2). Do đó: 2.1 2.2 S  S  S    3 (đvdt). OAB OAC OBC 2 2 M 1 E 0.25 Câu 1 7 A 1 1 D O C B H (3,0đ) 1 F N Ta có:  0
AEB  90 (góc nội tiếp chắn nửa đường tròn)  0 a)
 BEM  90 (kề bù với  ADB ) 0.75 Tứ giác BEMH có:   0 0 0
BEM  BHM  90  90  180
 Tứ giác BEMH nội tiếp Ta có:  0
AFB  90 (góc nội tiếp chắn nửa đường tròn)  AFB và  AHN có:    0 0.25 1 A chung ; AFB  AHN  90   AFB  AHN (g.g)
Gọi D là giao điểm thứ hai của AB với đường tròn ngoại tiếp  AMN    1 M  1 D  1  Vì    1 F  1 B  sđAE   và   1 B  1
M (tứ giác BEMH nội tiếp)  2  nên   1 F  1 M    1 F  1 D b)  AFC và  ADN có:    1 A chung ; 1 F  1 D   AFC  ADN (g.g) 0.75 AF AC    AF.AN  AC.AD AD AN
Mặt khác,  AFB  AHN (g.g) AF AB    AF.AN  AB.AH AH AN AB.AH
Do đó, AC.AD  AB.AH  AD  không đổi AC (vì A, C, B, H cố định)
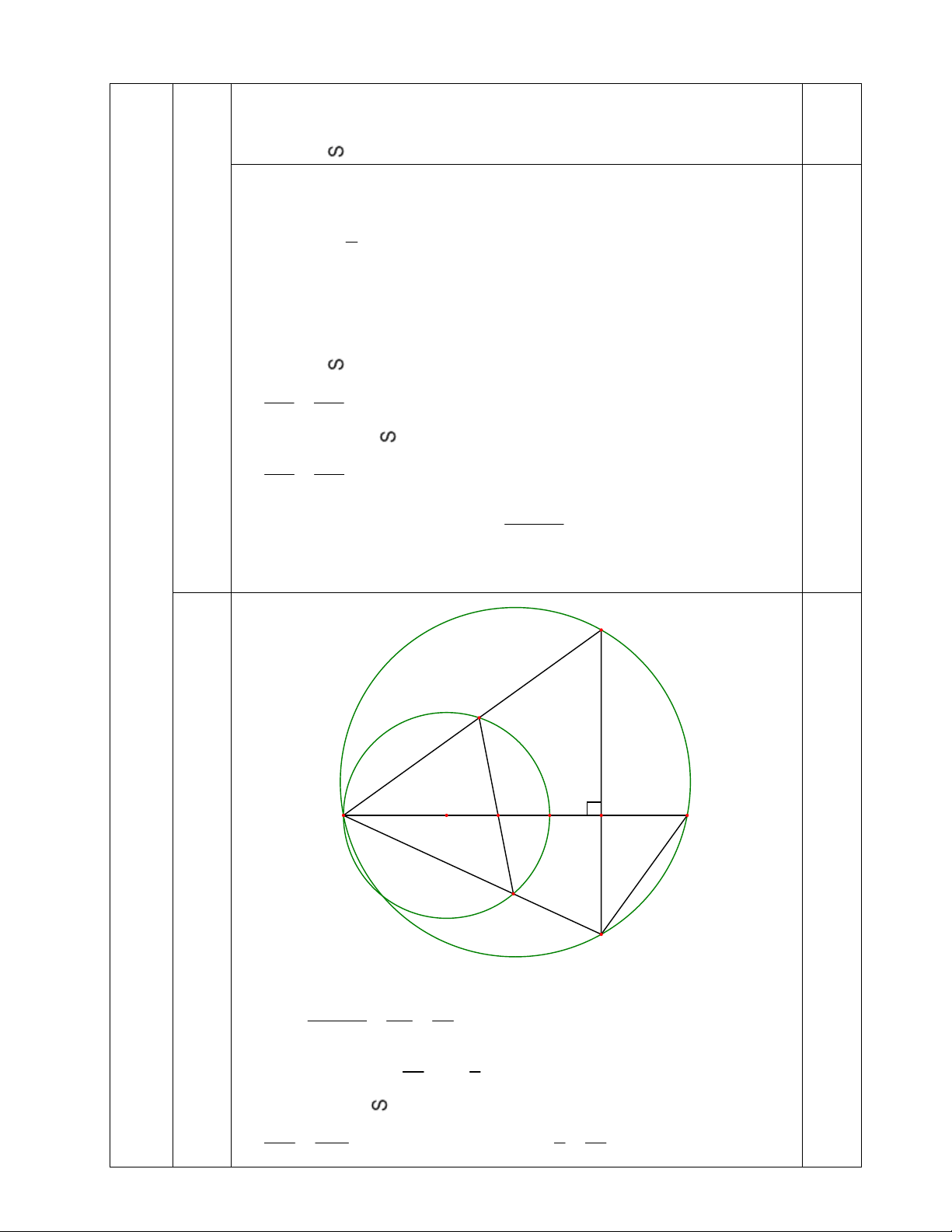
 Đường tròn ngoại tiếp  AMN luôn đi qua điểm D cố định (khác A). M 1 E A 1 D O C B H 1 c) 1 1.0 F 1 N
Với AB = 4cm, BC = BH = 1cm thì: AB.AH 4.5 20 AD    (cm) AC 3 3 20 5  HD  AD  AH   5  (cm) 3 3
Dễ thấy  AHM  NHD (g.g) AH HM 5 25  
 HM.HN  AH.HD  5  NH HD 3 3
Áp dụng bất đẳng thức Cô-si, ta có: 25 10 3
MN  HM  HN  2 HM.HN  2  (cm) 3 3 1 1 10 3 25 3 2       S AH.MN 5 (cm ) AMN 2 2 3 3 Dấu “=” xảy ra     HM  HN  1 M  1 N  1 F  1 N  EF / /MN  EF  AB 25 3 Vậy 2 minS  (cm )  EF  AB AMN 3 a  b1 ab
Đặt a = x2; b = y2 ( a,b  0) thì P  . 1 a2 1 b2 Vì a, b  0 nên: 2 2 2 2
(a  b)(1 ab)  a  a b  b  ab  a  ab  a(1 b ) 2 2
 a(1 2b  b )  a(1 b) Câu Lại có 2 2
(1 a)  (1 a)  4a  4a 8 1.0 a 1 b2 (1,0đ) 1  P   4a 1 b2 4 a  1 x  1  Dấu “=” xảy ra     b  0 y  0 1 x  1  Vậy m axP    4 y  0