ĐỀ THI TUYỂN SINH VÀO 10 BÌNH ĐỊNH 2023 MÔN: TOÁN (CHUNG) Bài 1: (2,0 điểm) 5
 x  3y  1
1. Giải hệ phương trình  .
 x  3y  5 x 3 x 4x  32
2. Cho biểu thức P   
, x  0 , x  16 . x  4 x  4 x 16
a) Rút gọn biểu thức P.
b) Tính giá trị lớn nhất của P. Lời giải. x 1 5
 x  3y 1 5
 x  3y 1 x 1  1. Ta có        4
 x  3y  5 6  x  6 5  .1 3y 1 y   .  3  
Vậy hệ phương trình có nghiệm duy nhất là  x y 4 ;  1;   .  3 
2. a) Điều kiện xác định: x  0 , x 16 (*). Ta có x      x x x 
 x 4 3 x x 4 4x 32 3 4 32  P     x  4 x  4
 x 4 x 4
 x 4 x 4
x4 x3x12 x4x32 x4 x 3x12 x 4x32   
x  4 x  4
 x 4 x 4 8  x   x 4 8 32  8    
x  4 x  4  x  4 x  4 . x  4 8 Vậy P 
với x  0 , x  16 . x  4
b) Với mọi x thỏa mãn điều kiện (*), ta có 8 x  4  1 1 4    P   2 . x  4 4 x  4
Với x = 0 (thỏa mãn (*)) thì P  2 . Vậy giá trị lớn nhất của P là 2, đạt được khi x = 0. Bài 2: (2,0 điểm) 1. Cho phương trình: 1 2
x  m  3 2 x 
m 1  0 (m là tham số). Tìm tất cả giá trị của m để 4
phương trình có hai nghiệm phân biệt x , x và thỏa mãn điều kiện 2x  x 8x x  34 . 1 2 2 1 2 1 2 Trang 1
2. Trong hệ tọa độ Oxy , cho các đường thẳng d  : y  ax  4 và d : y  3  x  2. 1 
a) Biết đường thẳng d  đi qua điểm A 1  ;5 . Tìm a .
b) Tìm tọa độ giao điểm của d với trục hoành, trục tung. Tính khoảng cách từ gốc tọa độ O 1 
đến đường thẳng d . 1  Lời giải. a) Xét phương trình 1 2
x  m  3 2 x  m 1  0 . (1) 4 2  1 
Ta có   m  3 2 2  41
m 1  m  6m  9     2
m  4  6m  5 .  4 
Phương trình (1) có hai nghiệm phân biệt khi và chỉ khi 5
  0  6m  5  0  m   . (*) 6 5 Vậy với m 
thì phương trình (1) có hai nghiệm phân biệt x , x . 6 1 2
Theo hệ thức Vi-ét, ta có
x  x  m  3 , 1 2 1 2 x x  m 1 . 1 2 4 Ta có
2 x  x 2 8x x  34 1 2 1 2    2m  32 1 2  8. m 1  34    4    2
m  m     2 2 6 9 2m  8  34 2 2
 2m 12m 18  2m 8  34  0
12m 24  0  m  2 (thỏa mãn (*)).
Vậy với m = 2 thì PT (1) có hai nghiệm phân biệt x , x thỏa mãn 2 x  x 8x x  34 . 1 2 2 1 2 1 2
2. a) Đường thẳng d  : y  ax  4 đi qua điểm A 1  ;5 khi và chỉ khi 5  . a  
1  4  a  4  5  a  9  . Vậy với a  9
 thì đường thẳng d  đi qua điểm A.
b) * Giả sử B  ;0
b  và C 0;c lần lượt là giao điểm của d với trục hoành và trục tung. 1  2
Vì d đi qua B nên 0  3.
 b  2  3b  2  0  b  . 1  3 Trang 2
Vì d đi qua C nên c  3  .0 2  2. 2   2  Vậy B ; 0 
 và C 0;2 lần lượt là giao điểm của d với trục hoành và trục tung. 1   3 
* Kẻ OH vuông góc BC tại H. Khi đó OH là khoảng cách từ O đến d . 1  2 Ta có OB 
, OC  2 . Áp dụng hệ thức lượng trong tam giác vuông OBC , ta có 3 1 1 1 1 1 5      2 2 2 2 2 OH OB OC  2  2 2    3  2 2  OH  2 10  OH   . 5 5 5 10
Vậy khoảng cách từ gốc tọa độ O đến đường thẳng d là . 1  5 Bài 3: (1,5 điểm)
Trong kì thi tuyển sinh vào lớp 10 THPT, cả hai trường A và B có tổng số 380 thí sinh dự thi. Sau
khi có kết quả, số thí sinh trúng tuyển của cả hai trường là 191 thí sinh. Theo thống kê thì trường
A có tỷ lệ trúng tuyển là 55% tổng số thí sinh dự thi của trường A, trường B có tỷ lệ trúng tuyển là
45% tổng số thí sinh dự thi của trường B. Hỏi mỗi trường có bao nhiêu thí sinh dự thi?
Lời giải: Gọi x, y lần lượt là số học sinh dự thi của trường A và B ( * x, y  ).
Vì cả hai trường A và B có 380 thí sinh dự thi nên
x  y  380 . (1)
Vì trường A có tỷ lệ trúng tuyển là 55% tổng số thí sinh dự thi của trường A nên số thí sinh trúng
tuyển của trường A là 0, 55x (thí sinh).
Vì trường B có tỷ lệ trúng tuyển là 45% tổng số thí sinh dự thi của trường B nên số thí sinh trúng
tuyển của trường B là 0, 45x (thí sinh).
Theo giả thiết, số lượng thí sinh trúng tuyển cả hai trường là 191. Do đó
0, 55x  0, 45 y  191. (2)
Từ (1) và (2) ta có hệ phương trình
x  y  380
0, 45x  0, 45y 171   
0,55x  0, 45y  191
0,55x  0, 45y  191 0,1x  20 x  200 x  200      
(thỏa mãn điều kiện).
x  y  380 200  y  380 y  180
Vậy trường A có 200 thí sinh dự thi, trường B có 180 thí sinh dự thi. Trang 3 Bài 4: (3,5 điểm)
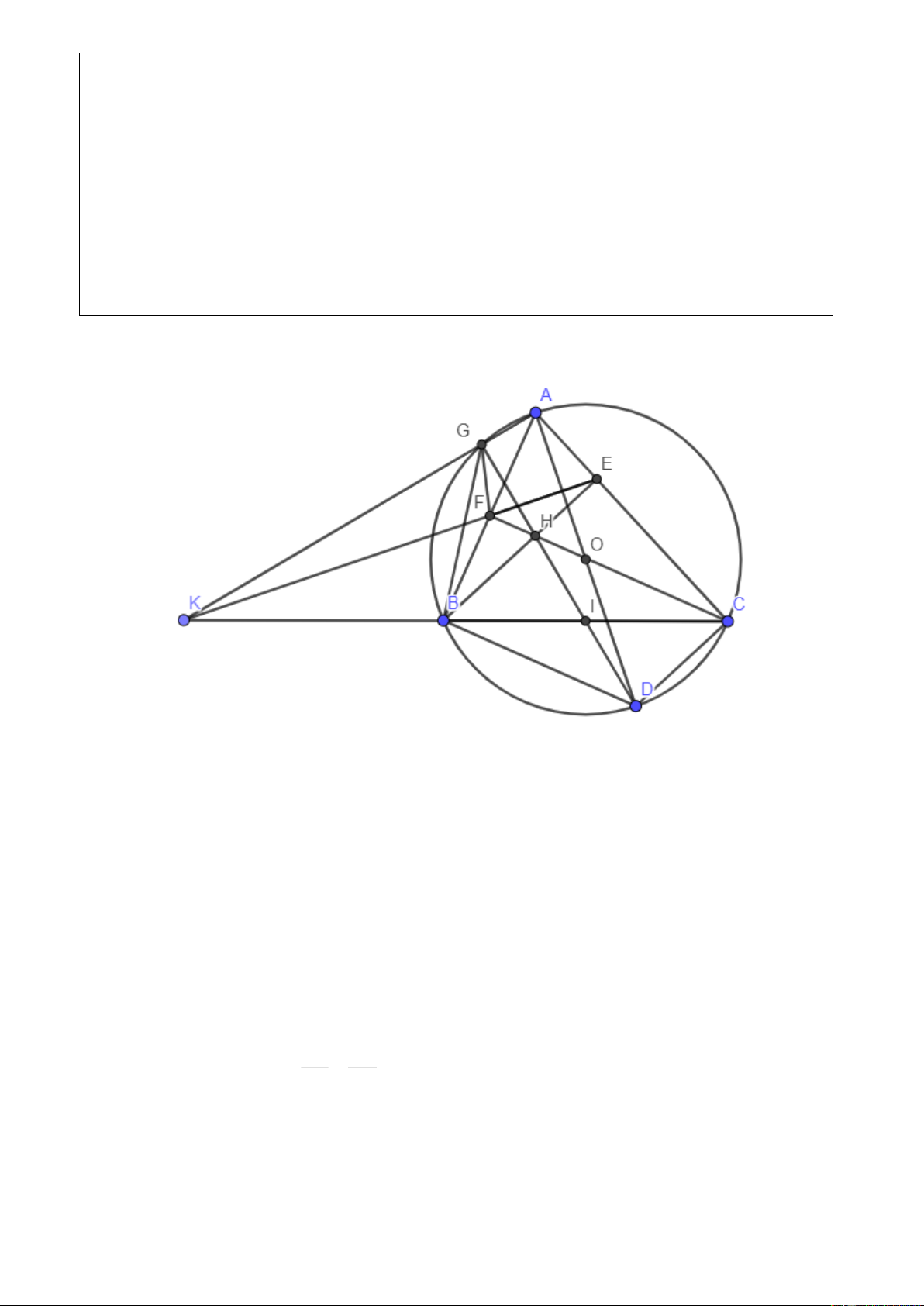
Cho tam giác ABC (AB < AC) nội tiếp đường tròn (O), các đường cao BE, CF của tam giác ABC
cắt nhau tại H, đường thẳng EF cắt BC tại K.
1. Chứng minh BCEF là tứ giác nội tiếp.
2. Chứng minh hai tam giác KBF và KEC đồng dạng, từ đó suy ra KB.KC = KF.KE.
3. Đoạn thẳng AK cắt lại đường tròn (O) tại điểm G khác A. Chứng minh các điểm A, G, F, E, H
cùng thuộc một đường tròn.
4. Gọi I là trung điểm BC, chứng minh HI vuông góc AK. Lời giải.
1. Ta có BFC  BEC  90 (vì BE và CF lần lượt là đường cao của ∆ABC)
 BCEF là tứ giác nội tiếp.
2. Vì BCEF là tứ giác nội tiếp nên BFE  KCE  180 .
Mà KFB  BFE  180 (hai góc kề bù) nên suy ra KCE  KFB . Xét K  BF và K  EC ta có
KCE  KFB (chứng minh trên), EKC là góc chung.  KB KF K  BF ∽ K  EC (g.g)    K . B KC  K . E KF . KE KC
3. Vì AGBC là tứ giác nội tiếp nên AGB  KCA  180 .
Mà AGB  KGB  180 (hai góc kề bù) nên KGB  KCA .
Xét ∆KGB và ∆KCA ta có Trang 4
KGB  KCA (chứng minh trên), AKC là góc chung.  KG KB K  GB∽ K  CA (g.g)    K . G KA  K . B KC . KC KA KG KF
Mà KB.KC = KE.KF (theo câu 2). Do đó K . A KG  K . E KF , suy ra  . KE KA
Xét ∆KGE và ∆KFA ta có KG KF  (chứng minh trên), KE KA AKE là góc chung.  K  GE ∽ K
 FA (c.g.c)  FEG  FAG .
Do đó AGFE là tứ giác nội tiếp. (1)
Mặt khác, ta có AFH  AEH  90 (vì BE và CF là đường cao của ∆ABC).
Suy ra AFHE là tứ giác nội tiếp. (2)
Từ (1) và (2) suy ra A, G, F, H, E cùng thuộc một đường tròn.
4. Kẻ đường kính AD của (O). Khi đó AGD  ABD  ACD  90 .
Mà A, G, F, H, E cùng thuộc một đường tròn nên AGH  AFH  AEH  90 .
Như vậy ta có AGD  AGH  90 hay G, H, D thẳng hàng. (3)
Ta có BH // CD (vì cùng vuông góc với AC),
CH // BD (vì cùng vuông góc với AB).
Do đó BHCD là hình bình hành. Mà I là trung điểm của BC nên H, I, D thẳng hàng. (4)
Từ (3) và (4) suy ra G, H, I, D thẳng hàng.
Mà AGD  90 nên HI vuông góc với AK. Bài 5: (1,0 điểm)
Cho các số thực dương a, b, c thỏa mãn a + b + c = 2024. Tìm giá trị lớn nhất của biểu thức a b c P    .
a  2024a  bc
b  2024b  ca
c  2024c  ab Lời giải. Từ giả thiết, ta có a a a   .
a  2024a  bc
a  a  b  c a  bc
a  a  ba  c Trang 5
Mặt khác theo bất đẳng thức Cauchy-Schwarz ta có         2 a b c a ac ab
 a  bc  a  ac  ab . Do đó a a a   .
a  a  ba  c
a  ac  ab
a  b  c
Hoàn toàn tương tự, ta cũng suy ra b b  ,
b  b  cb  a
a  b  c c c  .
c  c  ac  b
a  b  c Do đó a b c P     1.
a  b  c
a  b  c
a  b  c 2024
Với a  b  c 
(thỏa mãn giả thiết) thì P  1 . 3 2024
Vậy giá trị lớn nhất của P là 1, đạt được khi a  b  c  3
Ghi chú. i) Ngoài cách đánh giá trên, có thể trục căn thức ở mẫu rồi sử dụng BĐT AM-GM cho
trên tử, ta sẽ thu được đánh giá có dạng a ab  ca  .
a  2024a  bc
2ab  bc  ca
Thiết lập các BĐT tương tự rồi cộng lại ta cũng có điều tương tự.
ii) Chúng tôi đề xuất một phiên bản “nâng cấp hơn” của bài toán này.
Tổng quát: Cho a, b, c là các số thực dương. Chứng minh rằng a b c 3    .
a  m a  ba  c
b  m b  cb  a
c  m c  ac  b 1 2m
trong đó m là các số thực không âm cho trước.
Gợi ý. Trước hết hãy chứng minh a b c 3     .
a  ba  c
b  cb  a
c  ac b 2 Trang 6