Đề thi tuyển sinh vào lớp 10 Bình Định môn toán chuyên (có đáp án và lời giải chi tiết)

ĐỀ THI TUYỂN SINH VÀO 10 BÌNH ĐỊNH MÔN: TOÁN (CHUYÊN) Bài 1. (2,0 điểm)
1. Tính giá trị của biểu thức  x  x  x  2024 3 2 4 23 1
với x  3 3  2 .
2. a) Giả sử phương trình 2
x  ax  2  0 (a là tham số) có hai nghiệm x , x . Tính 3 3
P  x  x . 1 2 1 2 8 b) Cho 3 3  
 3 . Tìm một đa thức bậc 3, hệ số nguyên nhận  làm nghiệm. 3 Lời giải: 1. Ta có x 
  x     2 2 2 3 3 2 2 3 3
 27  x  4x  23  0 3 2
 x  x  x  x 2 4 23
x  4x  2  3  0 .
Do đó x  x  x  2024    2024 3 2 4 23 1 0 1  1.
2. a) Theo Định lý Viete, ta có x  x  a , x x  2 . Khi đó 1 2 1 2
P  x  x   x  x 3 3 3
3x x x  x  3  a  6 . a 1 2 1 2 1 2 1 2 2 b) Ta có 3    3 3 3 8 2  2  17 3 3 3     3  3. . 3.  3   6   3 3 3 3  3  3 3
 3 18 17  0 . Vậy P  x 3
 3x 18x 17 là một đa thức bậc 3 hệ số nguyên nhận  là nghiệm. Trang 1 Bài 2: (3,0 điểm) 1. Giải phương trình: 2
4x 1  2 4x 1  16x 1  2 ( x  ). 3 3
x  y  7
2. Giải hệ phương trình:   , x y   .  x  y  43xy  2  Lời giải: 1. Điề 1
u kiện xác định: x  . 4
Phương trình ban đầu tương đương
4x 1  2 4x 1  4x 1 4x 1  2  0
  4x 1  2 4x 1   1  0
 4x 1  2 (do 4x 1 1  0 )  4x 1 5 4  x 
(thỏa mãn điều kiện xác định). 4  
Vậy tập nghiệm của phương trình là 5 S    . 4 
2. Cộng theo vế hai phương trình của hệ, ta được 3 3
x  y  3xy  x  y  4 x  y  5
 x  y3  4x  y 5  0
 x  y   x  y2 1
 x  y  5  0   . (1) 2 2  1  19
Vì  x  y   x  y  5  x  y    0   nên  
1  x  y  1.  2  4
Thay y  1 x vào phương trình thứ hai, ta được
4  3x 1 x  2  x  1  2
 x  x  2  0   x  2. Với x  1
 thì y  2 . Với x  2 thì y  1.
Vậy tất cả các nghiệm của hệ ban đầu là  ; x y   2; 1; 1  ;2. Bài 3: (1,0 điểm)
Tìm tất cả các giá trị nguyên của n để 2
n  2026 là một số chính phương. Lời giải: Trang 2
Cách 1. Giả sử tồn tại số nguyên n sao cho 2 2
n  2026  k , với k  .
Khi đó k  nk  n  2026 .
Ta nhận thấy k  n và k  n có cùng tính chẵn lẻ. Do đó tích của chúng hoặc là số lẻ, hoặc là số
chia hết cho 4. Trong khi đó 2026 là số chẵn không chia hết cho 4, một mâu thuẫn.
Do đó không tồn tại số nguyên dương n sao cho 2
n  2026 là số chính phương.
Cách 2. Chú ý rằng một số chính phương khi chia cho 4 có số dư là 0 hoặc 1. Do đó 2
n  2026 chia cho 4 có số dư là 2 hoặc 3. Suy ra 2
n  2026 không là số chính phương. Bài 4: (3,0 điểm)
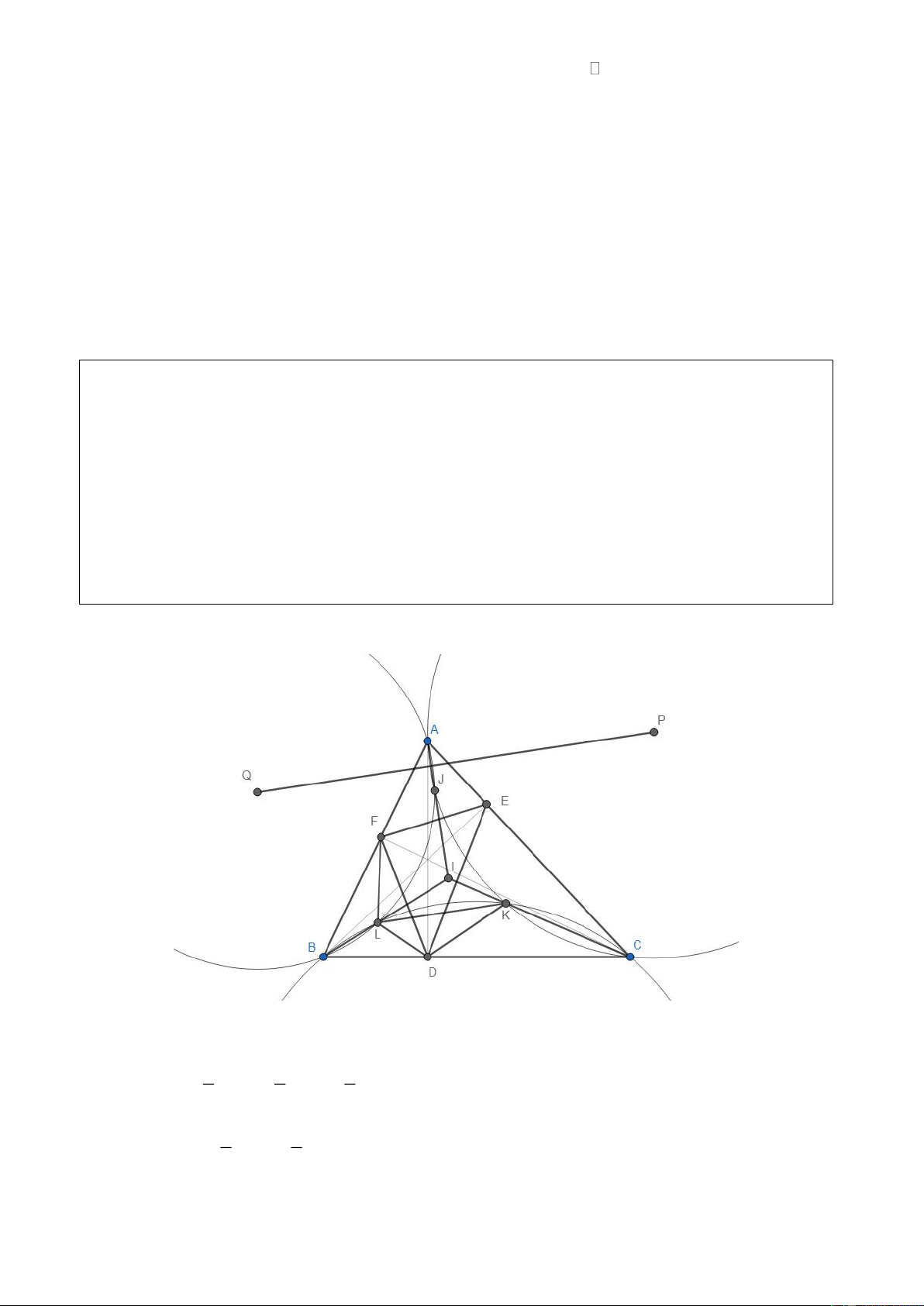
Cho tam giác nhọn ABC có các đường cao AD, BE, CF. Gọi K, L lần lượt là tâm đường tròn nội
tiếp của các tam giác CDE, BDF.
1. Chứng minh LDF  KDC .
2. Chứng minh hai tam giác LDF và KDC đồng dạng, hai tam giác LDK và FDC đồng dạng.
3. Chứng minh tứ giác BLKC nội tiếp.
4. Gọi P, Q lần lượt là tâm đường tròn ngoại tiếp các tam giác AKC, ALB. Chứng minh PQ // KL. Lời giải.
1. Vì ADC  AFC  90 nên AFDC là tứ giác nội tiếp. Tương tự, AEDB là tứ giác nội tiếp. Khi đó 1 1 1 LDF  BDF  BAC  CDE  CDK . 2 2 2 1 1 2. *Ta có LFD  BFD  C  DCK . 2 2
Xét ∆LDF và ∆KDC ta có Trang 3
LDF  KDC (câu 1.),
LFD  KCD (chứng minh trên). Suy ra L  DF ∽ K  DC (g.g).
* Từ kết quả câu 1, ta có LDK  LDF  FDK  KDC  FDK  FDC .
Xét ∆LDK và ∆FDC ta có
LDK  FDC (chứng minh trên), DL DK  (do L  DF ∽ K
 DC , chứng minh trên). DF DC Suy ra L  DK ∽ F  DC (c.g.c). 3. Ta có  BFD   C 
BLK  BLD  DLK  90 
  DFC  90    DAC  2   2       C  C  90    
 90  C 180  180  BCK . 2 2  
Suy ra tứ giác BLKC nội tiếp.
4. Gọi J là tâm đường tròn nội tiếp tam giác AEF. Chứng minh tương tự câu 3, ta chứng minh
được các AJLB, AJKC là các tứ giác nội tiếp. Do đó AJ là dây cung chung của đường tròn (P) và
(Q), suy ra AJ  PQ. (1)
Gọi I là tâm đường tròn nội tiếp tam giác ABC. Khi đó AJ, BL, CK cùng đi qua I. Ta có C A B
IJK  JKL  IJK  JKI  IKL  ACK  CAJ  LBC     90 . 2 2 2
Suy ra IJ  LK hay AJ  LK. (2)
Từ (1) và (2) suy ra PQ // LK.
Nhận xét. i) I là trực tâm tam giác IJK.
ii) Ta có thể mở rộng ý 3. của bài toán như sau:
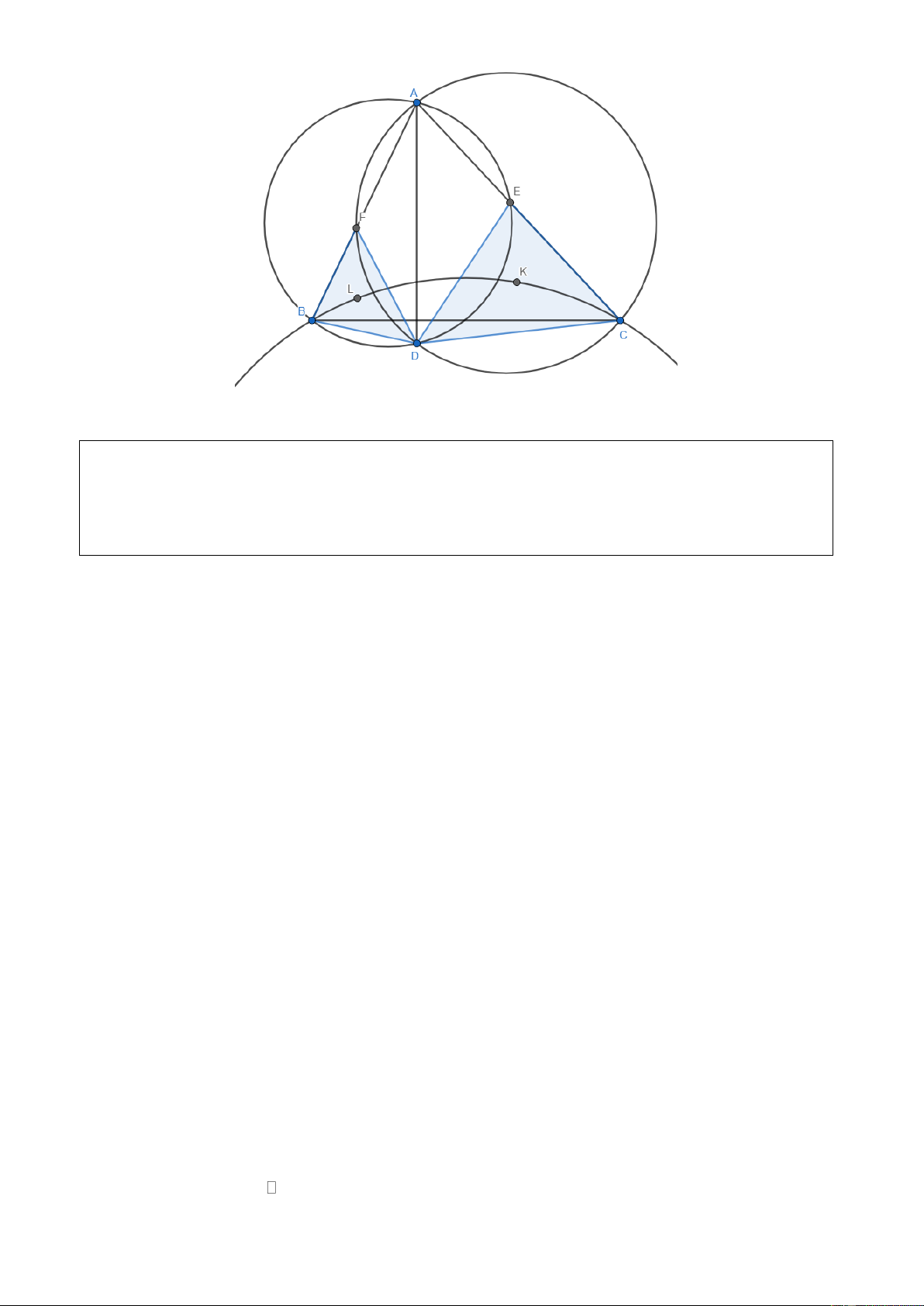
Cho tam giác ABC. D là một điểm sao cho AD  BC. Đường tròn ngoại tiếp các tam giác ABD,
ACD lần lượt cắt đường thẳng AC, AB tại giao điểm thứ hai E, F. Gọi K, L lần lượt là giao điểm
của tam giác EDC và FDB. Chứng minh rằng bốn điểm B, L, K, C cùng thuộc một đường tròn. Trang 4 Bài 5: (1,0 điểm)
Một học sinh viết lên bảng một dãy 2023 số nguyên dương thoả mãn trong dãy này có đúng 10 số
hạng phân biệt. Chứng minh rằng tồn tại một dãy các số hạng liên tiếp của dãy này sao cho tích
của chúng là một số chính phương. Lời giải:
Gọi a , a ,..., a
theo thứ tự là dãy gồm 2023 số nguyên dương được viết trên bảng, mỗi số trong 1 2 2023
dãy nhận một trong 10 giá trị b ,b ,..., b . 1 2 10
Với mỗi k = 1, 2,…, 2023, đặt P  a ...a là tích của k số hạng đầu tiền của dãy. Khi đó k 1 k    1k 2 k 10 k P  b b b k 1 2 10 ,
ở đây  ,..., lần lượt là số lần xuất hiện của b ,...,b trong k số hạng đầu tiên của dãy. 1k 10k 1 10
Xét 2023 bộ  , ,...,
theo modulo 2 (k = 1, 2,…, 2023), có tất cả 210 = 1024 trường hợp 1k 2k 10k  có dạng như sau:
(0,…, 0, 0), (0,…, 0, 1), (0,…, 1, 0),…, (1,…, 1, 1).
Theo Nguyên lý Dirichlet, tồn tại hai chỉ số m, n (giả sử 1 ≤ m < n < 2023) thỏa mãn  , ,...,   , ,..., mod 2 . 1m 2m 10m   1n 2n 10n    Khi đó    2 , 1n 1m 1    2 , 2n 2m 2 ...    2 , 10n 10m 10
trong đó  ,  ,...,   (do mỗi dãy  , ,...,
là dãy không giảm, với i = 1, 2,…, 10) 1 2 10 1 i i 2 i 2023 Như vậy ta có Trang 5 2 Pn 2 2 2    1 2 10 a a ...a   b b ...b  b b ...b m 1  m2 n 1 2 10  1 2 10 1 2 10  Pm
là một số chính phương. Ta có điều phải chứng minh.
Nhận xét. i) Ý tưởng sử dụng tổng/tích của k số hạng đầu tiên và kết hợp nguyên lý Dirichlet để
chứng minh một dãy các số liên tiếp có tổng/tích thỏa mãn điều kiện nào đó là một ý tưởng không mới. Chẳng hạn
1. (Vào 10 chuyên Toán Bình Định 2021-2022)
Cho n số nguyên dương a , a ,..., a có tổng bằng 2n – 1. Chứng minh rằng luôn tồn tại m số trong 1 2 n
n số đã cho có tổng bằng n.
2. Chứng minh rằng tồn tại số tự nhiên gồm toàn các chữ số 1 sao cho số tự nhiên đó chia hết cho 2023.
ii) Một số bài toán có nội dung tương tự:
1. Cho n số nguyên tố phân biệt và 2n + 1 số tự nhiên thỏa mãn mỗi số trong các số này không có
ước nguyên tố nào khác ngoài n số nguyên tố đã cho. Chứng minh rằng có thể chọn ra hai số trong
2n + 1 số này sao cho tích của chúng là số chính phương.
2. Cho 2002 số nguyên dương, mỗi số chỉ có ước nguyên tố không vượt quá 23. Chứng minh rằng
có thể tìm ra 4 số phân biệt có tích là lũy thừa bậc 4 của một số nguyên.
3. Cho A là tập gồm n số nguyên tố phân biệt và n + 1 số tự nhiên phân biệt sao cho mỗi số đều
không là số chính phương và chỉ có ước nguyên tố trong n số nguyên tố trong A. Chứng minh
rằng có thể chọn ra một số số có tích là một số chính phương. Trang 6