Đề thi tuyển sinh vào lớp 10 môn Toán năm 2021 – 2022 sở GD&ĐT Phú Thọ

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT PHÚ THỌ NĂM HỌC 2021-2022 Môn: TOÁN
Thời gian làm bài: 120 phút, không kể thời gian giao đề ĐỀ CHÍNH THỨC (Đề thi có 02 trang)
Thí sinh làm bài (cả phần trắc nghiệm và tự luận) vào tờ giấy thi.
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm)
Câu 1. Điều kiện xác định của biểu thức x  5 là A. x  5 B. x  5 C. x  5 D. x  5
Câu 2. Với giá trị nào của m thì hai đường thẳng y  12x  5  m và y  3x  m  3 cắt nhau
tại một điểm trên trục tung? A. 5. B. 3. C. 1. D. 4.
Câu 3. Hàm số y  m  2 x  4 đồng biến trên  khi A. m  2 B. m  2 C. m  2 D. m  2 x  3y 10
Câu 4. Nghiệm của hệ phương trình  là 2x  y  1  A. 3;  1 B. 1;3 C. 1;3 D. 3;  1
Câu 5. Với giá trị nào của m thì đồ thị hàm số y  m   2 2 x đi qua điểm . A (1;2) ? A. 0. B. 2. C. 4. D. 2  . Câu 6. Phương trình 2
x  2x  m  0 có hai nghiệm phân biệt khi A. m  1 B. m  1 C. m  1 D. m  1
Câu 7. Phương trình nào sau đây vô nghiệm? A. 2 x  x 1  0 B. 2 x  4x  4  0 C. 2 x  x 1  0 D. 2 x  5x  6  0
Câu 8. Cho ABC vuông tại A, đường cao AH. Biết AC  5c , m HC  4c . m Khi đó độ dài cạnh BC là A. 9c . m 25 25 5 B. c . m C. c . m D. c . m 4 16 4
Câu 9. Cho đường tròn tâm O, bán kính R  13(cm) , dây cung AB  24(cm) . Khoảng cách từ tâm O đến dây AB là A. 3cm. B. 4cm. C. 5cm. D. 6cm.
Câu 10. Cho tứ giác MNPQ nội tiếp một đường tròn. Biết  0 MNP   0 60 , PMQ  40 . Số đo  MPQ bằng N (Tham khảo hình vẽ) 600 A. 0 10 B. 0 20 C. 0 40 M 40° D. 0 50 Q P Trang | 1
PHẦN II. TỰ LUẬN (7,5 điểm) 7 x  6 x
Câu 1. (1,5 điểm). Cho biểu thức A   .x  0, x  4 x  4 x  2
a) Tính giá trị của biểu thức A khi x  16
b) Rút gọn biểu thức A. Câu 2. (2,0 điểm)
1. Cho đường thẳng d  : y  2mx  2m  3 và Parabol P 2 : y  x
a) Tìm m để đường thẳng d  đi qua A1;5.
b) Tìm m để đường thẳng d  tiếp xúc với Parabol P 2x  y  m 1
2. Cho hệ phương trình  ( m là tham số) 3x  y  4m 1
a) Giải hệ phương trình với m  2
b) Tìm m để hệ phương trình có nghiệm duy nhất  ; x y thỏa mãn 2 2x  3y  2
Câu 3. (3,0 điểm). Cho đường tròn Ođường kính AB. Trên tia đối của tia AB lấy điểm C
(C không trùng với B). Kẻ tiếp tuyến CD với đường tròn O (D là tiếp điểm), tiếp tuyến
tại A của đường tròn O cắt đường thẳng CD tại E.
a) Chứng minh rằng tứ giác AODE nội tiếp.
b) Gọi H là giao điểm của AD và OE, K là giao điểm của BE với đường tròn O
(K không trùng với B). Chứng minh  EHK   KB . A EA MO
c) Đường thẳng vuông góc với AB tại O cắt CE tại M. Chứng minh  1 EM MC
Câu 4. (1,0 điểm). Cho a, b, c là các số dương thỏa mãn 2 2 2
a  b  c  1. Tìm giá trị lớn
nhất của biểu thức A  1 2a1 2bc.
………………..Hết……………….
Họ và tên thí sinh: ………………………………………………..SBD:……….
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm. Trang | 2
Đáp án – Thang điểm dự kiến.
I. PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm)
- Mỗi câu đúng được 0,25 điểm. Câu 1 2 3 4 5 6 7 8 9 10 Đáp án A C D B C D A B C B
PHẦN II. TỰ LUẬN (7,5 điểm) Câu Nội dung Điểm
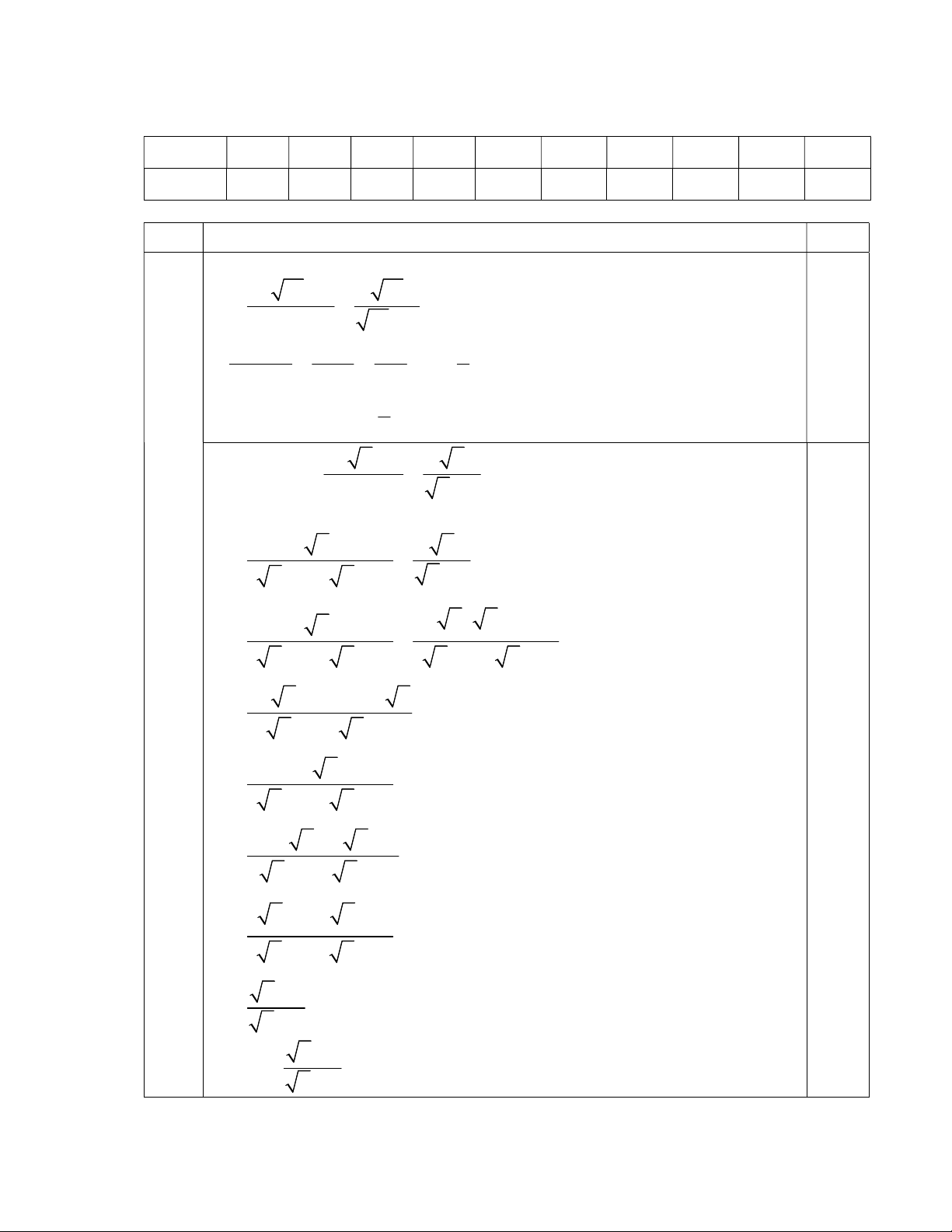
a)Thay x  16 (TMĐK) vào biểu thức ta được 7 16  6 16 A   16  4 16  2 0,25 28  6 4 11 1     2  12 4  2 6 6 0,25 1 Vậy với x = 16 thì A = 6 7  x  6 x b)Rút gọn A   x  4 x  2 Với x  0, x  4 có 7 x  6 x A    x  2 x  2 x  2 x  x   x 2 7 6  0,25 A   
x  2 x  2  x  2 x  2 1 7 x  6  x  2 x A   x  2 x  2 x  5 x  6 0,25 A   x  2 x  2 x  2 x  3 x  6 A   x  2 x  2  0,25 x  2 x  3 A   x  2 x  2 x  3 A  0,25 x  2 x  3 Vậy A  x  2 Trang | 3
1.a Tìm m để đường thẳng d  : y  2mx  2m  3 đi qua A1;5.
Do (d) đi qua A1;5. Thay x 1; y  5 vào phương trình đường thẳng ta 0,25 được: 5  2 .
m 1 2m  3  4m  8  m  2
Vậy với m = 2 thì đường thẳng d  : y  2mx  2m  3 đi qua A1;5. 0,25
1.b Tìm m để đường thẳng d  tiếp xúc với Parabol P
Phương trình hoành độ giao điểm của (d) và (P) là 2 2 2
x  2mx  2m  3  x  2mx  2m  3  0*   m2 '   m   2 2 3  m  2m  3 0,25
Để d  tiếp xúc với Parabol P thì phương trình (*) có nghiệm kép hay m 1 0,25 ' 2
  0  m  2m  3  0  m   1 m  3  0   m  3 Vậy m = 1 hoặc m = -3 2x  y  2 1 2x  y 1
2.a. Thay m  2 vào phương trình ta được    3  x  y  4.2 1 3  x  y  9 2x  y 1 5x 10 x  2 x  2 0,5         3  x  y  9 2x  y 1 2.2  y 1 y  3
KL: Với m  2 hệ phương trình có nghiệm duy nhất  ; x y  2;3 2 1  2.b. Ta thấy 
nên hệ phương trình có nghiệm duy nhất với  m 3 1 2x  y  m 1 5  x  5m x  m x  m        3  x  y  4m 1 3  x  y  4m 1 3  m  y  4m 1 y  m 1 0,25 Thay vào phương trình 2 2x  3y  2 ta được: 2 2 2 2m  3m  
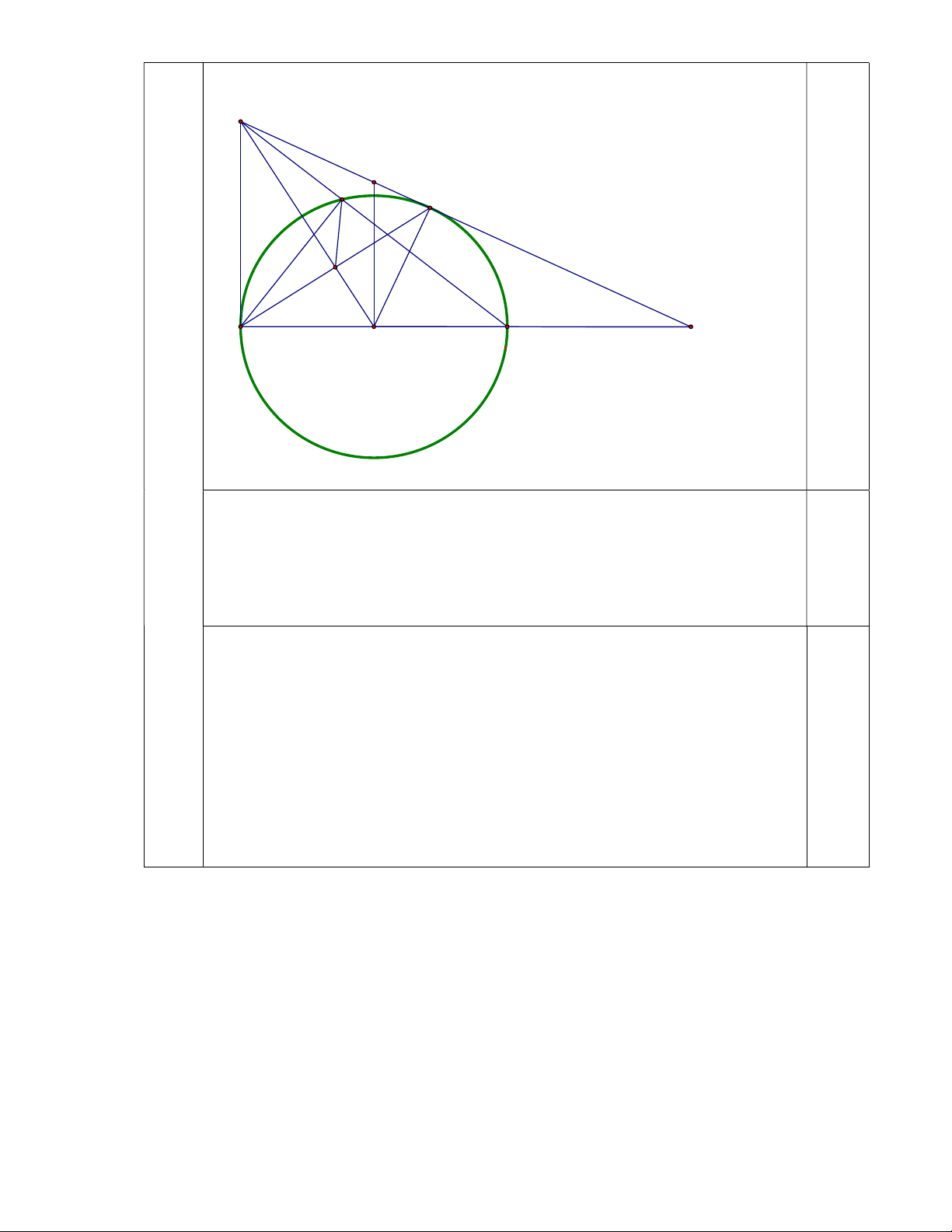
1  2  2m  3m  5  0  2m  5m   1  0 m  1    5 0,25 m   2  5  Vậy m   1  ;   2 Trang | 4 Hình vẽ: E M K D H A O B C 3 a). Tứ giác AODE có:  0
EAO  90 (Vì EA là tiếp tuyến của đường tròn (O)) 0,5  0
EDO  90 (Vì ED là tiếp tuyến của đường tròn (O)) Do đó:  EAO   0 0 0 EDO  90  90  180 0,5
Vậy tứ giác AODE nội tiếp đường tròn.
b). Ta có EA  ED (Theo tính chất của hai tiếp tuyến cắt nhau)
OA  OD (Cùng là bán kính của đường tròn (O)) 0,25
Do đó EO là đường trung trực của AD hay EO  AD   0 EHA  90  0
AKB  90 (Góc nội tiếp chắn nửa đường tròn)   0 EKA  90 0,25
Vậy hai điểm kề nhau H, K cùng nhìn xuống đoạn thẳng EA một góc
vuông nên tứ giác AHKE nội tiếp đường tròn. Suy ra:  EHK  
EAK (Hai góc nội tiếp cùng chắn một cung) 0,25 Mà  EAK   KBA (Cùng phụ với  KAB ) 0,25 Vậy:  EHK   KB . A Trang | 5 c). Ta có OM  AB (gt)
EA  AB (Vì EA là tiếp tuyến của đường tròn (O)) Suy ra OM / /EA 0,25  MEO  
AEO (Theo tính chất của hai tiếp tuyến cắt nhau)  MOE  
AEO (Hai góc so le trong và OM / /EA) Vậy  MOE  
MEO hay tam giác MEO cân tại M  ME  MO 0,25
Áp dụng hệ quả của định lí Ta-lét cho tam giác CAE OM / /EA OM MC EA CE EA MC  EM Ta có:      AE CE OM MC EM MC 0,25 EA EM EA MO  1   1 (Chú ý là ME  MO ) 0,25 EM MC EM MC
Cho a, b, c là các số dương thỏa mãn 2 2 2
a  b  c  1. Tìm giá trị lớn nhất
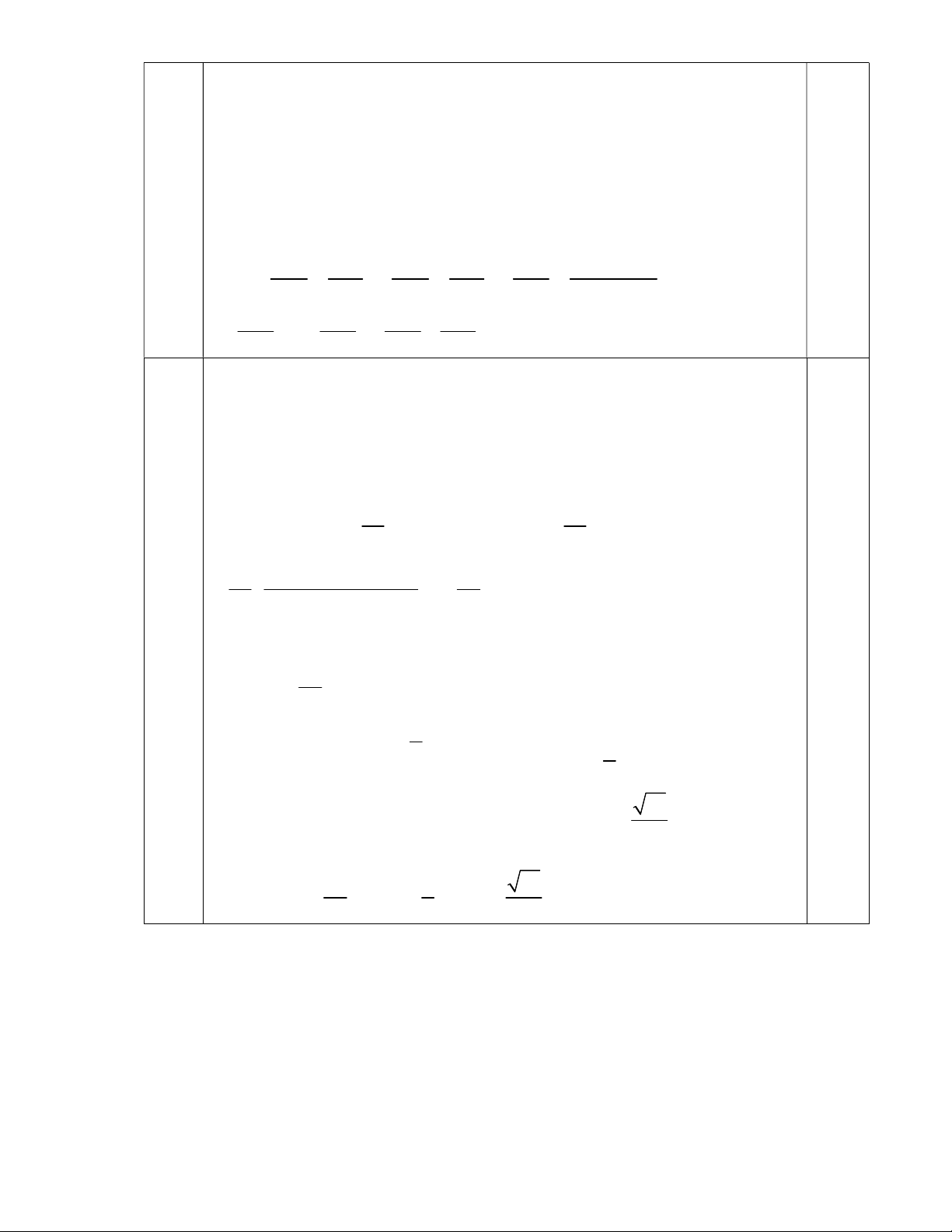
của biểu thức A  1 2a1 2bc. Ta có: 2 2 2bc  b  c A    a 2 2
 b  c     a 2 1 2 1 1 2 2  a  ( vì 2 2 2 a  b  c  1) Có 0,25   a 2  a  1    a 2  a  1 1 2 2 6 12 18 9   2 10  9a  2 18  9a  54 54 2 2 2
1  10  9a 18  9a  98     54  2  27 0,25 4  2 do9a  4 12a 98 Do đó A  0,25 27  2 a    2 3 a      3
Dấu “=” xảy ra khi: b  c    2 2 2 10 a  b  c 1 b   c    6 2 2 1  0  9a 18  9a 0,25 98 2 10 Vậy Max A = Khi a  ; b  c  27 3 6 Trang | 6