Đề thi tuyển sinh vào lớp 10 năm 2023-2024 môn toán 10 Sở GD Phú Yên (có đáp án và lời giải chi tiết)

SỞ GIÁO DỤC ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 PHÚ YÊN
NĂM HỌC: 2023 – 2024 Môn: TOÁN
Khoá thi ngày: 01/6/2023
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
I. Trắc nghiệm (3,0 điểm)
Câu 1: Biểu thức   2 2 3 có giá trị là A. 3  2 . B. 2  3 . C. 7  4 3 . D. 1.
Câu 2: Tìm x thỏa mãn biểu thức 2  x  2 . A. x  0 . B. x  2 . C. x  2 . D. x  4 .
Câu 3: Hàm số nào sau đây là không phải là hàm số bậc nhất? x 2
A. y  1 x . B. y  . C. y  . D. y  2  x  2  . 2 x
Câu 4: Đường thẳng y  x  3 đi qua điểm M ( m ;1) . Khi đó
A. m 1 .B. m  2 . C. m  3 . D. m  4 .
ax  by  2
Câu 5: Tìm các giá trị của a và b để hệ phương trình 
có nghiệm (1; 1)
2ax  by 1
A. a  1;b  1  . B. a  1  ;b 1.
C. a  1;b  1.
D. a  2;b  1  .
Câu 6: Cho m , n là nghiệm của phương trình 2
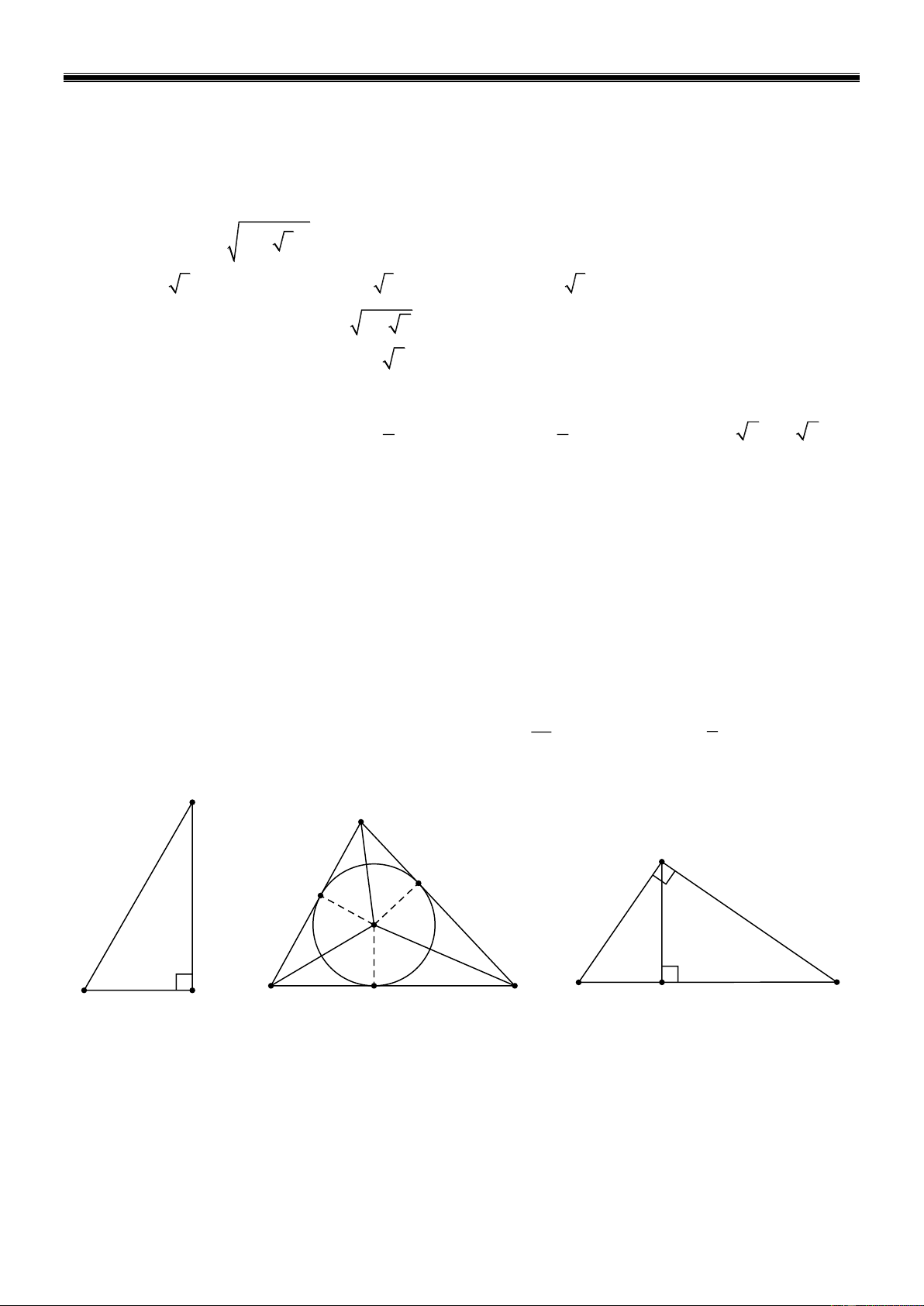
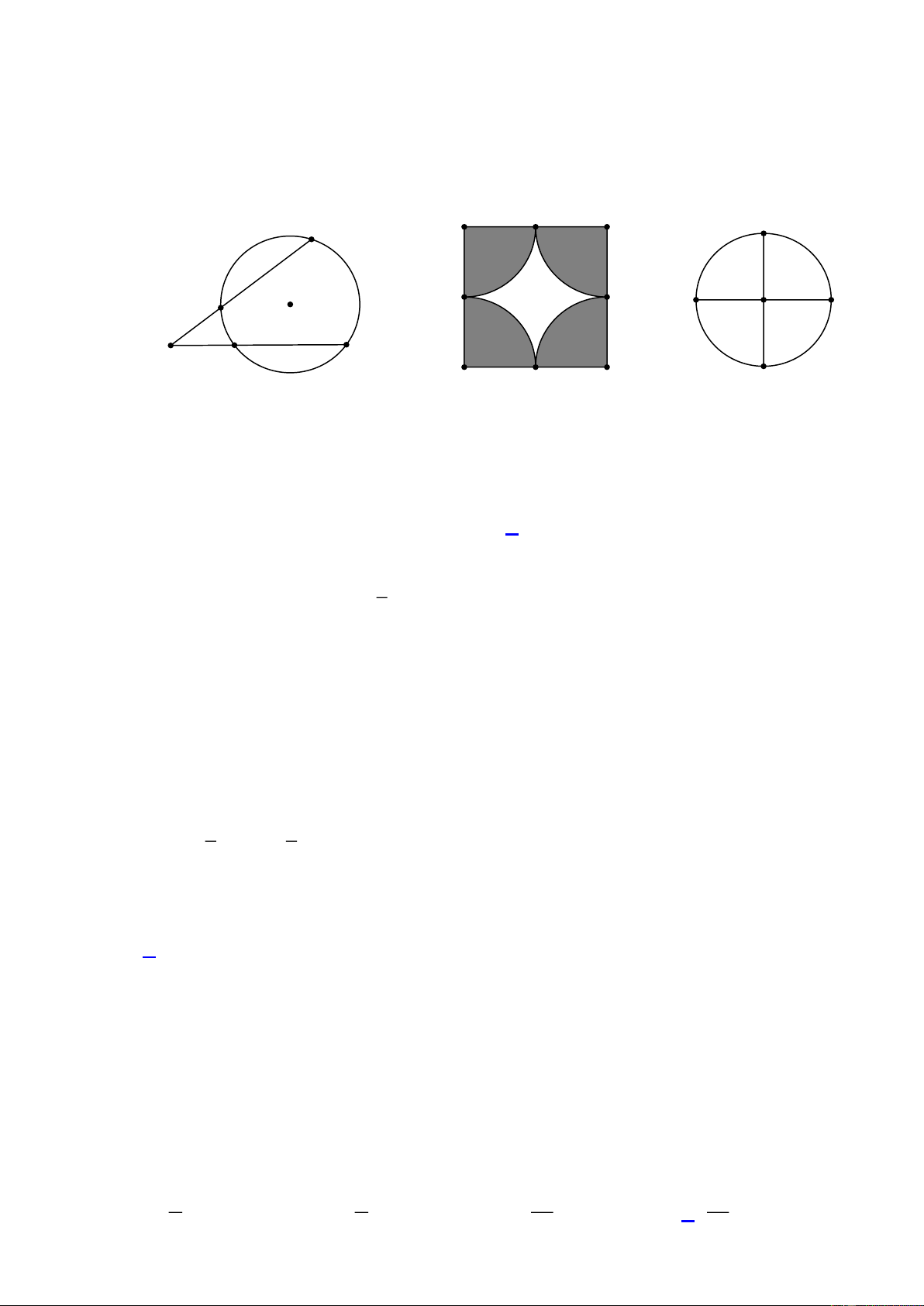
x  mx  n  0 , với m  0 ; n  0 . Thế thì tổng các nghiệm của phương trình bằng 1 1 A. 1. B. 1. C. . D. . 2 2 A N T F E 6 m I 3 m S K M G B H P R Hình 1 Hình 2 Hình 3 Câu 7:
Một cái thang AB dài 6m tựa vào tường, chân thang cách tường 3m ( Hình 1). Tính góc tạo
bởi thang AB và tường AH . A. 30 . B. 45. C. 60 . D. 90 . Câu 8:
Tam giác nhọn MNP có đường tròn  I  nội tiếp, với E , F ,G là các tiếp điểm ( Hình 2).
Khẳng định nào sau đây không đúng?
A. IGP  90 .
B. ME  MG .
C. MNI  INP .
D. N ; I ;G thẳng hàng. Trang 1 Câu 9:
Cho tam giác STR vuông tại T , đường cao TK ( Hình 3). Khẳng định nào sau đây sai? 1 1 1 A.   . B. 2 2 2
SR  ST  TR . C. 2
ST  SK.SR . D. T .
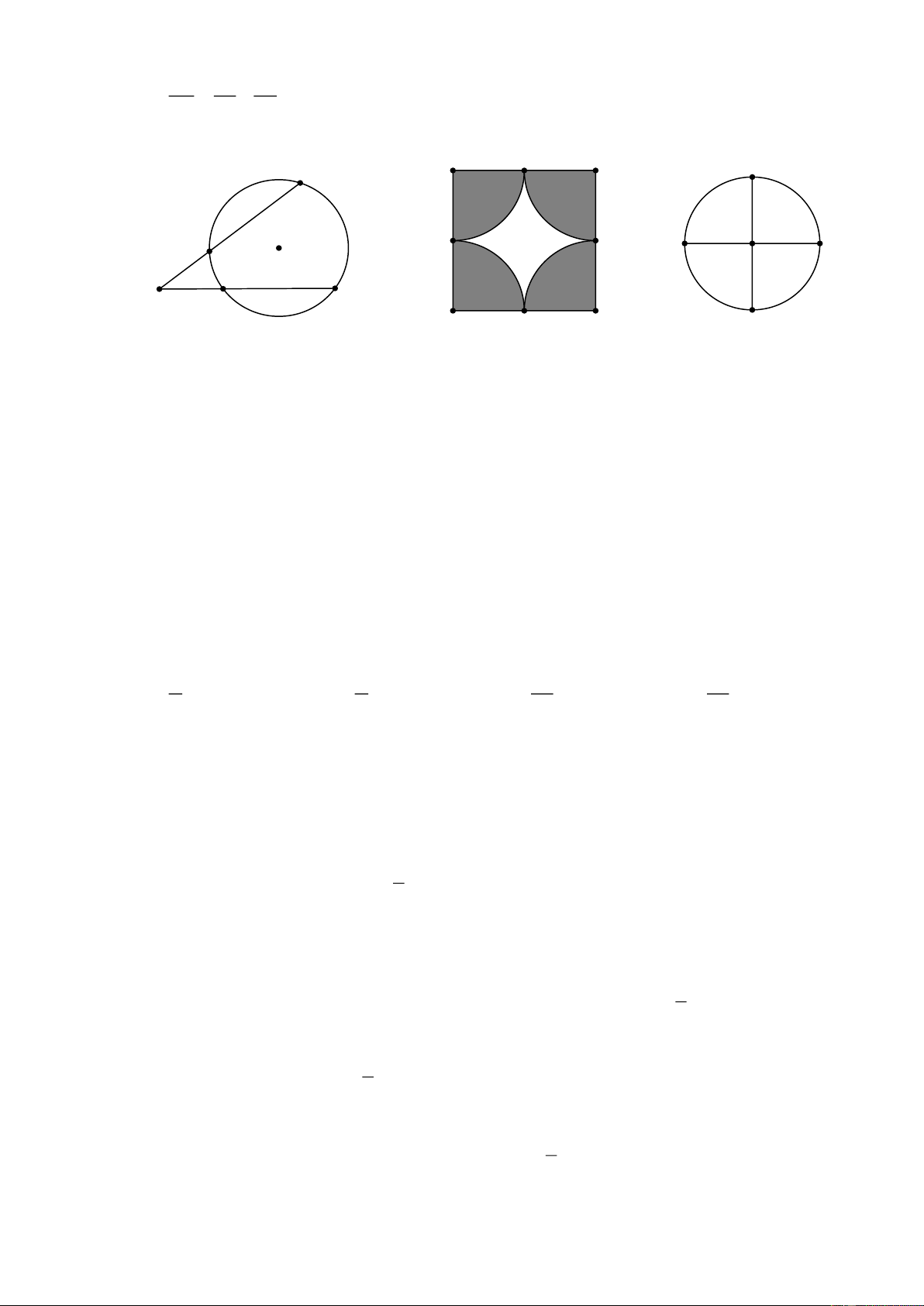
S TR  TK.SR . TK TS TR M D E B R H K N P Q J O A K C G I F S Hình 4 Hình 5 Hình 6
Câu 10: Từ một điểm A nằm ngoài đường tròn  J  , kẻ hai cát tuyến AHB và AKC ( Hình 4). Biết
BAC  40 ; các cung HB, BC, CK có cùng độ dài. Tìm số đo HCK . A. 30 . B. 20. C. 15 . D. 10 .
Câu 11: Hình vuông DEFG có cạnh bằng 2 cm ; M ; N; I ; K là trung điểm các cạnh (Hình 5). Tính diện
tích phần màu trắng giới hạn bởi 4 cung tròn KM ; MN ; NI ; IK (tâm là các đỉnh hình vuông). A. 2 4   (cm ) . B. 2   4(cm ). C. 2  (cm ) . D. 2 4(cm ) .
Câu 12: Đường tròn O có bán kính bằng1cm . Hai đường kính PQ và RS vuông góc với nhau (Hình
6). Tính độ dài cung lớn PR .   3 3 A. (cm) . B. (cm) . C. (cm) . D. (cm) . 4 2 4 2
II. Tự luận (7,0 điểm)
Câu 13. (1,5 điểm) Giải các phương trình, hệ phương trình sau: a) 2
2x  5x  2  0 xy  3  b)  3
 x  3y  2xy  0 1
Câu 14. (2,0 điểm) Cho hai hàm số 2 y  
x và y  ax  b . 2
a) Tìm các hệ số a, b biết đường thẳng y  ax  b đi qua điểm M  2  ; 2  , N 4;  1 .
b) Với các giá trị a, b vừa tìm được, hãy: 1
+ Tìm giao điểm của đường thẳng y  ax  b và đồ thị hàm số 2 y  
x bằng phương pháp 2 đại số. 1
+ Vẽ đồ thị hai hàm số 2 y  
x và y  ax  b trên cùng một mặt phẳng tọa độ. 2
Câu 15. (1,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình 2
Một khu đất hình chữ nhật có tỷ số hai kích thước là
. Người ta làm một sân bóng đá mini 5 3
người ở giữa, chừa lối đi xung quanh (lối đi thuộc khu đất). Lối đi rộng 2 m và có diện tích 2
224 m . Tính các kích thước của khu đất. Câu 16. (2,0 điểm) Trang 2
Cho tam giác ABC vuông tại A , có AB  3 cm, AC  4 cm . Đường tròn tâm B bán kính BA
và đường tròn tâm C bán kính CA cắt nhau tại điểm thứ hai D .
a) Chứng minh rằng tứ giác ABDC là tứ giác nội tiếp.
b) Tính độ dài đoạn AD .
c) Một đường thẳng d quay quanh A cắt B tại E E  A và cắt C tại F F  A . Gọi
M là giao điểm của EB và FC . Khi d thay đổi thì điểm M chạy trên đường nào?
-------------------------------@Hết@----------------------------------- HƯỚNG DẪN GIẢI
I. Trắc nghiệm (3,0 điểm)
Câu 1: Biểu thức   2 2 3 có giá trị là A. 3  2 . B. 2  3 . C. 7  4 3 . D. 1. Lời giải   2 2 3  2  3  2  3
Câu 2: Tìm x thỏa mãn biểu thức 2  x  2 . A. x  0 . B. x  2 . C. x  2 . D. x  4 . Lời giải
2  x  2 (1) ĐKXĐ: x  0
(1)  2  x  4 
x  2  x  4 ( TMĐK)
Câu 3: Hàm số nào sau đây là không phải là hàm số bậc nhất? x 2
A. y  1 x . B. y  . C. y  . D. y  2  x  2  . 2 x Lời giải 2 Hàm số y 
không có dạng y  ax  b nên không là hàm số bậc nhất. x
Câu 4: Đường thẳng y  x  3 đi qua điểm M ( m ;1) . Khi đó
A. m 1 B. m  2 . C. m  3 . D. m  4 . Lời giải
Đường thẳng y  x  3 đi qua điểm M ( m;1) nên 1 m  3  m  2
ax  by  2
Câu 5: Tìm các giá trị của a và b để hệ phương trình 
có nghiệm (1; 1)
2ax  by 1
A. a  1;b  1  . B. a  1  ;b 1.
C. a  1;b  1.
D. a  2;b  1. . Lời giải
ax  by  2 Hệ phương trình  có nghiệm (1; 1)
2ax  by 1  .1 a  .( b 1  )  2 a  b  2 3  a  3 a 1         2 .1 a  b( 1  ) 1 2a  b 1 b   2a 1 b  1 Trang 3
Câu 6: Cho m , n là nghiệm của phương trình 2
x  mx  n  0 , với m  0 ; n  0 . Thế thì tổng các nghiệm của phương trình bằng 1 1 A. 1. B. 1. C. . D. . 2 2 Lời giải
m , n là nghiệm của phương trình 2
x  mx  n  0 nên theo định lý Vi et có
m  n  m  .
m n  n  m 1 ( Vì n  0 )
Khi đó m n  1 
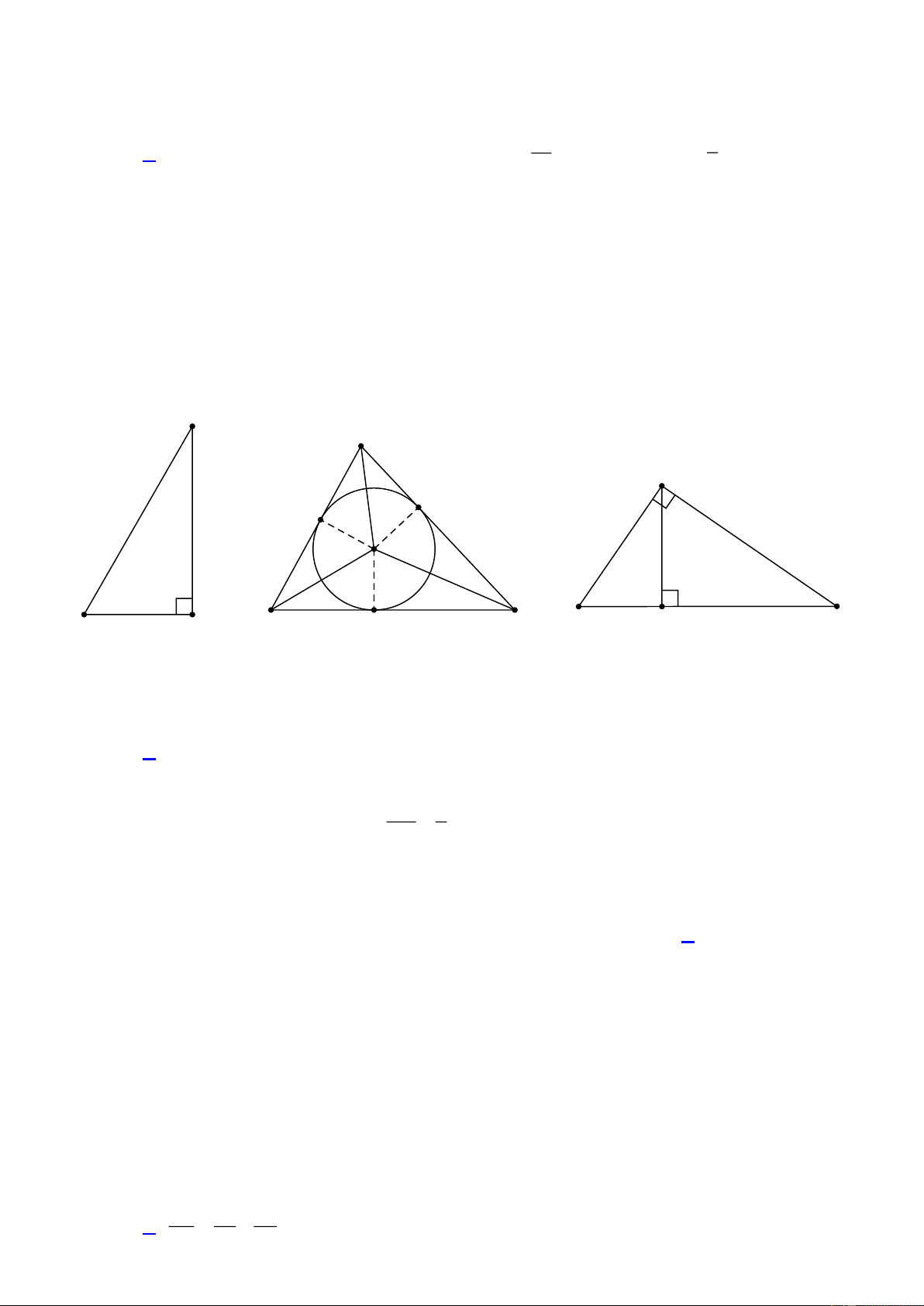
Vậy tổng hai nghiệm bằng 1. A N T F E 6 m I 3 m S K M G B H P R Hình 1 Hình 2 Hình 3 Câu 7:
Một cái thang AB dài 6m tựa vào tường, chân thang cách tường 3m ( Hình 1). Tính góc tạo
bởi thang AB và tường AH . A. 30 . B. 45. C. 60 . D. 90 . Lời giải BH 1 ABH 
vuông tại H có sin A A 30     . AB 2 Câu 8:
Tam giác nhọn MNP có đường tròn  I  nội tiếp, với E , F ,G là các tiếp điểm ( Hình 2).
Khẳng định nào sau đây không đúng?
A. IGP  90 .
B. ME  MG .
C. MNI  INP .
D. N ; I ;G thẳng hàng. Lời giải
Tam giác nhọn MNP có đường tròn  I  nội tiếp, với E , F ,G là các tiếp điểm nên :
IG  MP  IGP  90
ME  MG ( tính chất hai tiếp tuyến cắt nhau).
MNI  INP ( vì tâm I là giao điểm 3 đường phân giác). Đáp án D sai. Câu 9:
Cho tam giác STR vuông tại T , đường cao TK ( Hình 3). Khẳng định nào sau đây sai? 1 1 1 A.   . B. 2 2 2
SR  ST  TR . C. 2
ST  SK.SR . D. T .
S TR  TK.SR . TK TS TR Trang 4 Lời giải
Tam giác STR vuông tại T , đường cao TK nên ta có: 2 2 2
SR  ST  TR ( định lý Pytago) 2
ST  SK.SR ; T .
S TR  TK.SR ( hệ thức giữa cạnh và đường cao trong tam giác vuông) Khẳng định A sai. M D E B R H K N P Q J O A K C G I F S Hình 4 Hình 5 Hình 6
Câu 10: Từ một điểm A nằm ngoài đường tròn  J  , kẻ hai cát tuyến AHB và AKC ( Hình 4). Biết
BAC  40 ; các cung HB, BC, CK có cùng độ dài. Tìm số đo HCK . A. 30 . B. 20. C. 15 . D. 10 . Lời giải Xét đườ 1
ng tròn  J  có BAC  sđ C
B  sđ HK   40 ( góc có đỉnh nằm ngoài đường tròn) 2
 sđ BC  sđ HK  80 (1)
Mặt khác sđ HB  sđ BC  sđ CK  sđ HK  360
Mà các cung HB, BC, CK có cùng độ dài  sđ HB  sđ BC  sđ CK
Do đó 3.sđ BC  sđ HK  360 (2)
Từ (1) và (2) suy ra  4.sđ BC  360  80  440  sđ BC  0 11 
 sđ HK 110 80  30 1 1 HCK  sđ HK  .30  15 . 2 2
Câu 11: Hình vuông DEFG có cạnh bằng 2cm; M ; N; I ; K là trung điểm các cạnh (Hình 5). Tính diện
tích phần màu trắng giới hạn bởi 4 cung tròn KM ; MN ; NI ; IK (tâm là các đỉnh hình vuông). A. 2 4   (cm ) . B. 2   4(cm ). C. 2  (cm ) . D. 2 4(cm ) . Lời giải
Diện tích hình vuông DEFG là: 2 2.2  4 (cm )
Diện tích 4 cung tròn tại 4 góc hình vuông (tâm là các đỉnh hình vuông) bằng diện tích hình
tròn bán kính 1cm và bằng: 2 2 .1   (cm )
Vậy diện tích phần màu trắng giới hạn bởi 4 cung tròn KM ; MN ; NI ; IK là 2 4   (cm )
Câu 12: Đường tròn O có bán kính bằng1cm . Hai đường kính PQ và RS vuông góc với nhau (Hình
6). Tính độ dài cung lớn PR .   3 3 A. (cm) . B. (cm) . C. (cm) . D. (cm) . 4 2 4 2 Trang 5 Lời giải
Hai đường kính PQ và RS vuông góc với nhau nên POR  90 .1.90 
Độ dài cung nhỏ PR là l   (cm) PR 180 2  3
Độ dài cung lớn PR là : 2.1  (cm) . 2 2
II. Tự luận (7.0 điểm)
Câu 13. (1,5 điểm) Giải các phương trình, hệ phương trình sau: a) 2
2x  5x  2  0 xy  3  b)  3
 x  3y  2xy  0 Lời giải a) 2
2x  5x  2  0 Ta có: 2
Δ  5  4.2  2  9  0 5  9 1 5  9
Suy ra phương trình có 2 nghiệm phân biệt là: x    ; x   2 1 2 2.2 2 2.2  
Vậy tập nghiệm của phương trình là: 1 S   ; 2  2  xy  3  xy  3  xy  3  b)     
3x  3y  2xy  0
3x  3y  6  0   x  y  2 Suy ra ,
x y là nghiệm của phương trình 2
t  2t  3  0
Vì a  b  c  1 ( 2
 )  3  0 nên phương trình có hai nghiệm phân biệt là: t  1  ;t  3 1 2
Vậy hệ phương trình có 2 nghiệm là:  ; x y  3;  1 ;  ; x y   1  ;3 . 1
Câu 14. (2,0 điểm) Cho hai hàm số 2 y  
x và y  ax  b . 2
a) Tìm các hệ số a, b biết đường thẳng y  ax  b đi qua điểm M  2  ; 2  , N 4;  1 .
b) Với các giá trị a, b vừa tìm được, hãy: 1
+ Tìm giao điểm của đường thẳng y  ax  b và đồ thị hàm số 2 y  
x bằng phương pháp 2 đại số. 1
+ Vẽ đồ thị hai hàm số 2 y  
x và y  ax  b trên cùng một mặt phẳng tọa độ. 2 Lời giải
a) Tìm các hệ số a, b biết đường thẳng y  ax  b đi qua điểm M  2  ; 2  , N 4;  1 .
Do đường thẳng y  ax  b đi qua điểm M  2  ; 2
  nên thay x  2  , y  2
 vào y  ax  b ta được phương trình 2   2  a b  2  a b  2  (1)
Do đường thẳng y  ax  b đi qua điểm N 4; 
1 nên thay x  4, y  1 vào y  ax  b ta được phương
trình 1  4a  b  4a  b  1  2
Từ (1) và (2) ta có hệ phương trình: Trang 6    1  2
 a  b  2  6a  3 a       2 4a  b  1 b  1 4a   b      1   1 a  Vậy  2 b   1
b) Với các giá trị a, b vừa tìm được, hãy: 1
+ Tìm giao điểm của đường thẳng y  ax  b và đồ thị hàm số 2 y  
x bằng phương pháp đại số. 2  1 a  1 Với 
2 thì phương trình đường thẳng có dạng y  x 1 2 b   1
Xét phương trình hoành độ 1 1
giao điểm của y  x 1 và 2 y   x ta có 2 2 1 1 2
 x  x 1 2 2 2
 x  x  2 2
 x  x  2  0
 x  2x   1  0 x  2    x  1 1 Với x  2
 thay vào y  x 1 ta được y  2 2 1 1
Với x 1 thay vào y 
x 1 ta được y   2 2 1 1  
Vậy giao điểm của đồ thị hàm số y  x 1 và 2 y   x là    1 2, 2 ; 1,    2 2  2  1
+ Vẽ đồ thị hai hàm số 2 y  
x và y  ax  b trên cùng một mặt phẳng tọa độ. 2 1
* Vẽ đồ thị hàm số y  x 1 2   Đồ 1 thị hàm số y 
x 1 là đường thẳng đi qua hai điểm A   1 2, 2 ; B 1  ,    2  2  1 * Vẽ đồ thị hàm số 2 y   x 2 Ta có bảng giá trị sau: x -2 -1 0 1 2 1 1 1 2 y   x -2  0  -2 2 2 2
 Đồ thị hàm số là đường cong parabol đi qua các điểm       A   1 1 0; 0 ; 2; 2 ; B 1;  ;C 1  ; ; D 2; 2        2   2  Trang 7 1 Hệ số a  
 0 nên parabol có bề cong hướng xuống. Đồ thị hàm số nhận Oy làm trục đối xứng. 2 1
Ta vẽ được đồ thị hàm số 2 y   x như sau: 2
Câu 15. (1,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình 2
Một khu đất hình chữ nhật có tỷ số hai kích thước là
. Người ta làm một sân bóng đá mini 5 3
người ở giữa, chừa lối đi xung quanh (lối đi thuộc khu đất). Lối đi rộng 2 m và có diện tích 2
224 m . Tính các kích thước của khu đất. Lời giải 2
Vì mảnh đất là hình chữ nhật có tỉ số hai kích thước là . 3
Gọi 2x m là chiều rộng của mảnh đất (x  0)
3x  m là chiều dài của mảnh đất.
Khi đó diện tích cả mảnh đất là: 2
x  x  x  2 2 3 6 m  .
Phần sân bóng có chiều rộng là: 2x  4m
Phần sân bóng có chiều dài là: 3x  4m
Diện tích phần sân bóng là:
 x  x  2 2
 x  x  x 
 x  x   2 2 4 3 4 6 8 12 16 6 20 16 m .
Khi đó diện tích lối đi là: 2 x   2 x  x   2 2
 x  x  x   x   2 6 6 20 16 6 6 20 16 20 16 m .
Theo đề ra ta có diện tích lối đi bằng 2 224 m nên
20x 16  224  20x  240  x  12m.
Vậy khu đất có chiều dài là 36 m , chiều rộng là 24 m . Câu 16. (2,0 điểm) Trang 8
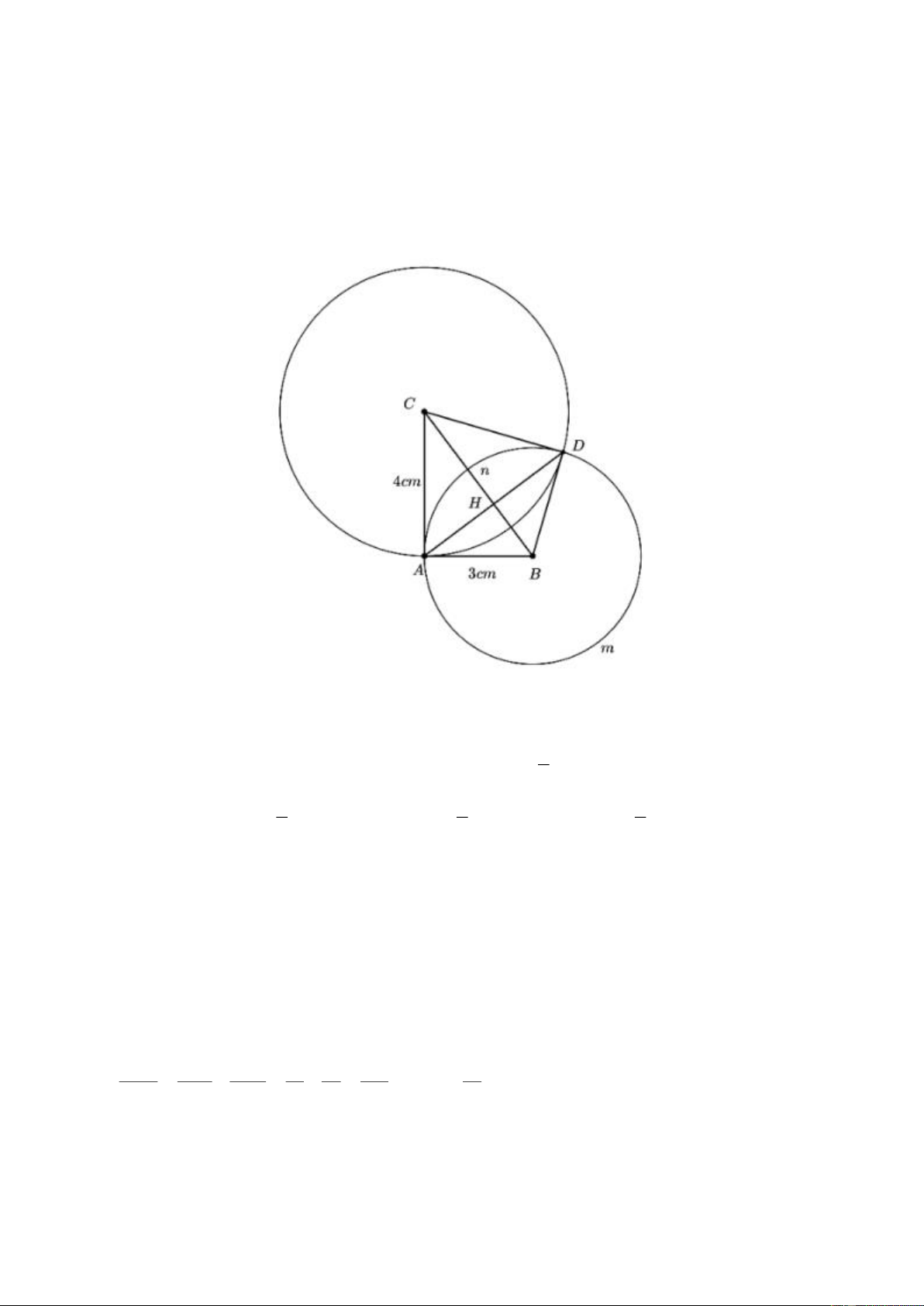
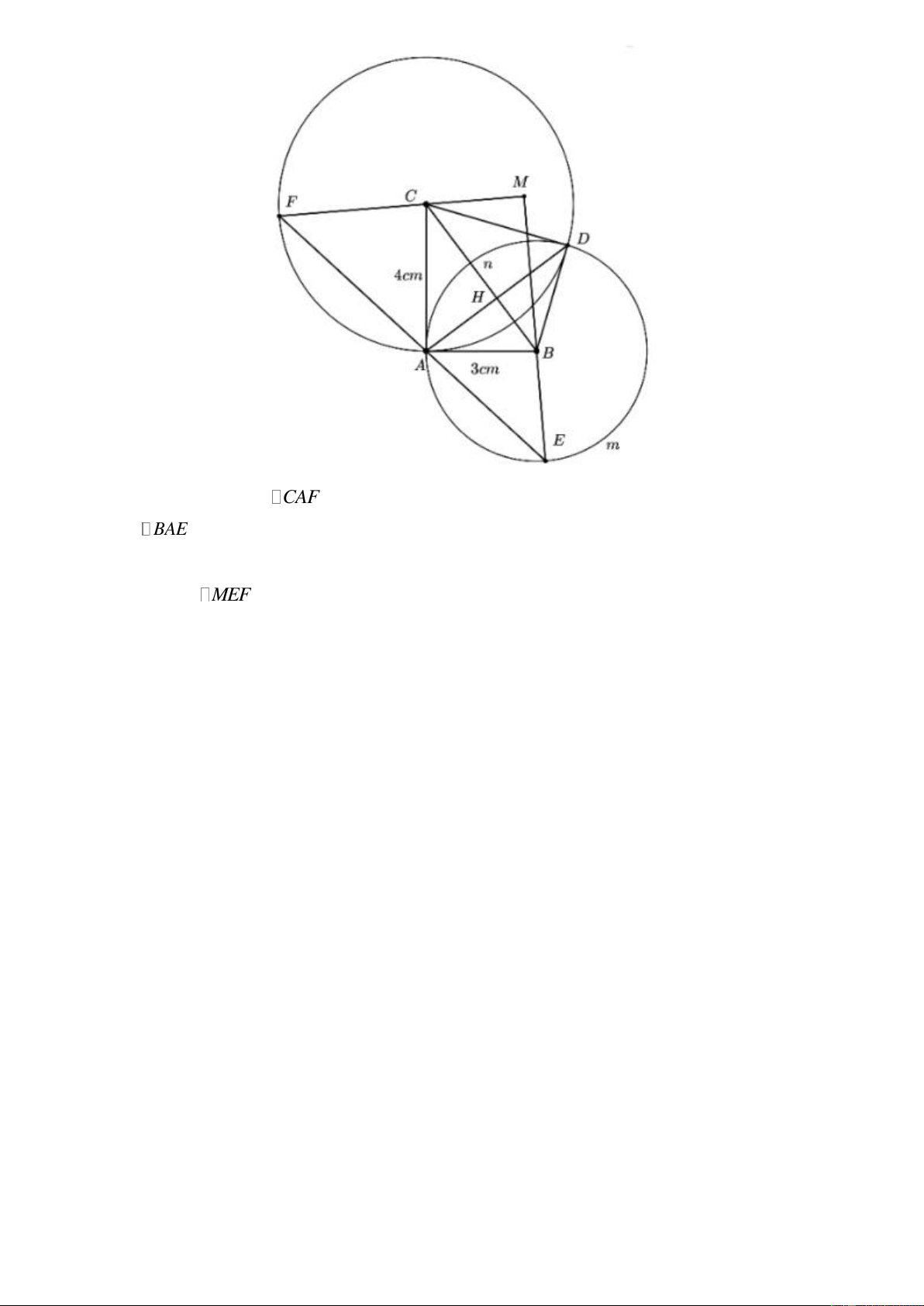
Cho tam giác ABC vuông tại A , có AB  3 cm, AC  4 cm . Đường tròn tâm B bán kính BA
và đường tròn tâm C bán kính CA cắt nhau tại điểm thứ hai D .
a) Chứng minh rằng tứ giác ABDC là tứ giác nội tiếp.
b) Tính độ dài đoạn AD .
c) Một đường thẳng d quay quanh A cắt B tại E E  A và cắt C tại F F  A . Gọi
M là giao điểm của EB và FC . Khi d thay đổi thì điểm M chạy trên đường nào? Lời giải
a) Chứng minh tứ giác ABDC nội tiếp được.
Xét đường tròn tâm B có ABD  sđ AnD 1
ACD là góc có đỉnh bên ngoài đường tròn tâm B nên ACD 
sđAmDsđAnD 2 1  1 1
ABD  ACD  sđ AnD 
sđAmDsđAnD  sđAmDsđAnD 360180 2 2 2
 ABDC là tứ giác có tổng 2 góc đối bằng 180
 ABDC là tứ giác nội tiếp
b) Tính độ dài đoạn AD .
Ta có BA  BD  3 cm và CA  CD 4 cm
 BC là trung trực của AD  BC  AD
Gọi H là giao điểm của AD và BC Xét ABC 
vuông tại A , đường cao AH 1 1 1 1 1 25 12        AH  (cm) 2 2 2 2 2 AH AB AC 3 4 144 5
c) Một durờng thẳng d quay quanh A cắt  B tại E E  A và cắt C tại F  F  A . Gọi M là giao
điểm của EB và FC . Khi d thay đổi thì điểm M chạy trên đường nào? Trang 9
Ta có CF  CA  4cm nên CAF cân tại C  F  CAF (tính chất)
Tương tự BAE cân tại B nên E  BAE (tính chất)
Mà CAF  BAE  180  CAB  180  90  90
 E  F  90  MEF vuông tại M (tổng các góc trong một tam giác)
Xét tứ giác MCAB có CMB  CAB  90  90  180
Mà 2 góc này ở vị trí đối diện nên MCAB nội tiếp có đường kính BC
Mà BC cố định nên M luôn thuộc đường tròn đường kính BC cố định. Trang 10