SỞ GD&ĐT NGHỆ AN
KÌ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2023 - 2024 MÔN: TOÁN 10 --------------------
Thời gian làm bài: 120 PHÚT
(Đề thi có ___ trang)
(không kể thời gian phát đề) Câu 1. ( 2.5 điểm) a)Tính A  4  49  64   b)Rút gọn biểu thức x 1 4x P    .  
, với x  0 và x 1. 2 2 x x 1  
c)Tìm giá trị của b để đường thẳng y  2x  b 1 cắt trục hoành tại điểm có hoành độ bằng 1. Câu 2. ( 2.0 điểm) a)Giải phương trình 2
x  3x 10  0 . b)Cho biết phương trình 2
x  5x  3  0 có hai nghiệm dương phân biệt là x , x . Không giải phương 1 2 x 1 x 1 1  2 
trình, tính giá trị của biểu thức T  . 2 x  5x 1 2 Câu 3. ( 2.0 điểm)
a)Một cửa hàng kinh doanh xe đạp nhập về một kho hàng gồm hai loại: loại I có giá 2 triệu đồng/xe và
loại II có giá 6 triệu đồng/xe. Biết rằng lô hàng nói trên có 50 xe với tổng số tiền mà cửa hàng
phải thanh toán là 160 triệu đồng. Hỏi cửa hàng đã nhập về bao nhiêu xe loại I và bao nhiêu xe loại II?
b)Bạn An bỏ một viên bi đặc không thấm nước vào một lọ thủy tinh chứa nước dạng hình trụ có bán kính
đường tròn đáy bằng 1,5cm . Tính thể tích viên bi bạn An bỏ vào lọ thủy tinh ( cho   3,14 ;
xem độ dày của lọ không đáng kể và nước không thất thoát ra ngoài).
Câu 4 ( 3 điểm). Cho tam giác nhọn ABC  AB  AC , các đường cao AD , BE , CF
DBC, E  AC, F  AB cắt nhau tại H .
a)Chứng minh AEHF là tứ giác nội tiếp.
b)Gọi O là trung điểm của đoạn thẳng BC , M là giao điểm của tia EF và CB . Chứng minh rằng
FAD  OFC và 2 OC  . OD OM .
c)Chứng minh rằng hai đường thẳng MH và AO vuông góc với nhau.  2  x  
1 2y  1  4
Câu 5 ( 0,5 điểm). Giải hệ phương trình  2 2 2 2
x y 1  y x 1  x y 1  LỜI GIẢI Câu 1. a)Tính A  4  49  64 . Ta có: A  4  49  64  2  7  8 17   b)Rút gọn biểu thức x 1 4x P    .  
, với x  0 và x 1. 2 2 x x 1      Ta có: x 1 4x x 1 4x P    .    .  2 x 2 2 x x 1   2 x x 1
c)Tìm giá trị của b để đường thẳng y  2x  b 1 cắt trục hoành tại điểm có hoành độ bằng 1.
Yêu cầu bài toán tương đương với 0  2.1 b 1  b  1  . Câu 2. a)Giải phương trình 2
x  3x 10  0 . Ta có:   49
Phương trình có hai nghiệm phân biệt là x  2 và x  5 . 1 2 Trang 1 b)Cho biết phương trình 2
x  5x  3  0 có hai nghiệm dương phân biệt là x , x . Không giải phương 1 2 x 1 x 1 1  2 
trình, tính giá trị của biểu thức T  . 2 x  5x 1 2    Theo đị x x 5 nh lí Vi-et ta có: 1 2  x .x  3  1 2
Khi đó, x 1 x 1  x .x  x  x 1 3 51 9 1  2  1 2 1 2
Do x là nghiệm của phương trình đã cho nên 2 2
x  5x  3  0  x  5x  3 . 1 1 1 1 1 Suy ra, 2
x  5x  3  5x  3  5x  5 x  x  3  5.5  3  22 . 1 2 1 2  1 2  9 Vậy T  . 22 Câu 3.
a)Một cửa hàng kinh doanh xe đạp nhập về một kho hàng gồm hai loại: loại I có giá 2 triệu đồng/xe và
loại II có giá 6 triệu đồng/xe. Biết rằng lô hàng nói trên có 50 xe với tổng số tiền mà cửa hàng phải thanh
toán là 160 triệu đồng. Hỏi cửa hàng đã nhập về bao nhiêu xe loại I và bao nhiêu xe loại II?
Gọi số xe loại I là x ; x  0
Gọi số xe loại II là y ; y  0 .
Tổng số xe cửa hàng đã nhập bằng 50 xe nên: x  y  50
Tổng số tiền cửa hàng phải thanh toán là 160 triệu đồng nên: 2x  6 y  160 . x  y  x  35
Từ đó ta có hệ phương trình 50    (thỏa mãn)
2x  6 y  160  y  15
Vậy cửa hàng đã nhập về 35 xe loại I và 15 xe loại II.
b)Bạn An bỏ một viên bi đặc không thấm nước vào một lọ thủy tinh chứa nước dạng hình trụ có bán kính
đường tròn đáy bằng 1,5cm . Tính thể tích viên bi bạn An bỏ vào lọ thủy tinh ( cho   3,14 ; xem độ dày
của lọ không đáng kể và nước không thất thoát ra ngoài).
Thể tích của khối nước dâng them là: V   r h   2 2 3 . . 3,14. 1, 5 .0, 5  3, 5325cm
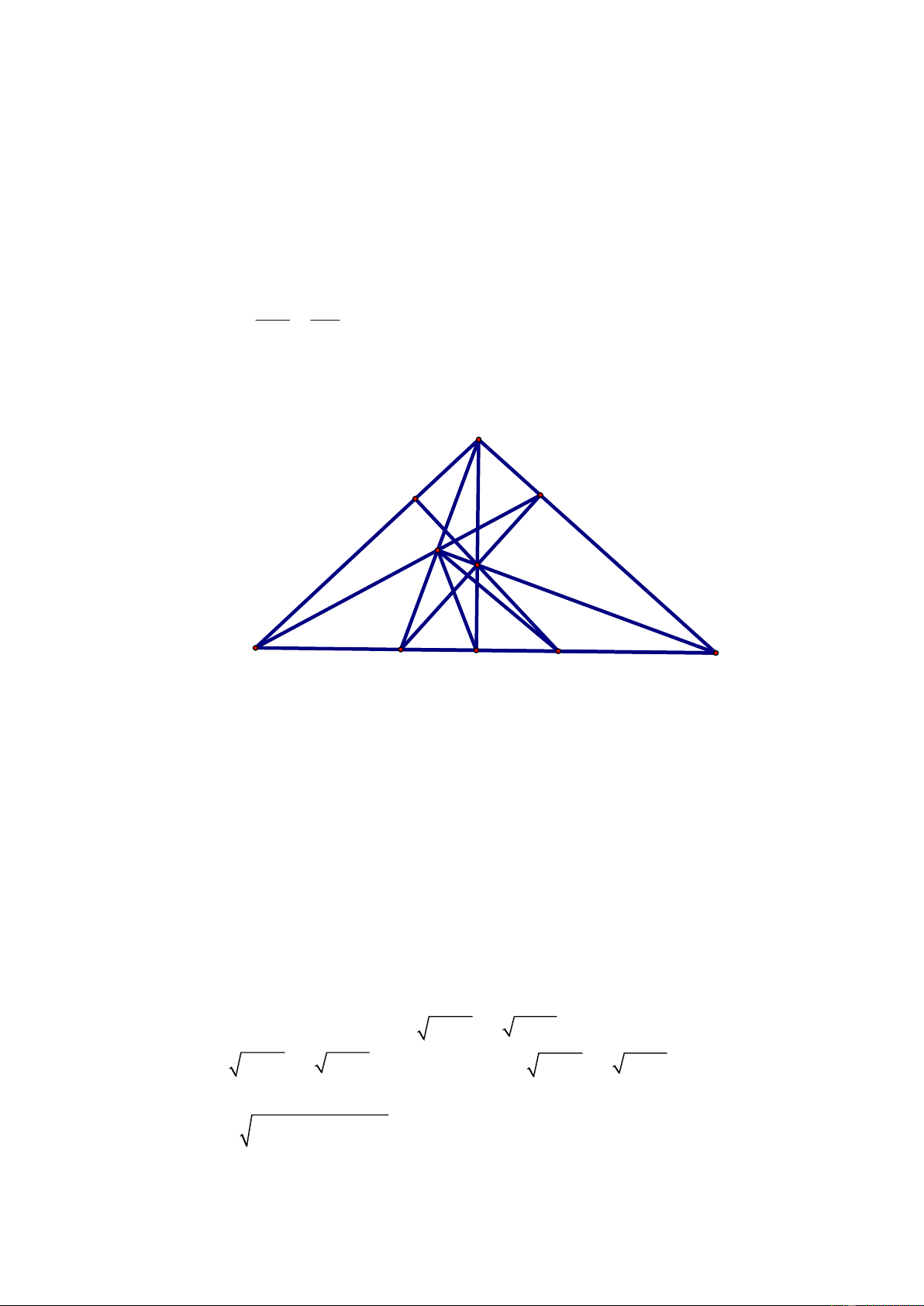
Câu 4 ( 3 điểm). Cho tam giác nhọn ABC  AB  AC , các đường cao AD , BE , CF
DBC, E  AC, F  AB cắt nhau tại H .
a)Chứng minh AEHF là tứ giác nội tiếp. A E F H B D C
Do BE  AC  AEH  90
Do CF  AB  AFH  90
Từ đó suy ra AFH  AEH  180  AEHF là tứ giác nội tiếp.
b)Gọi O là trung điểm của đoạn thẳng BC , M là giao điểm của tia EF và CB . Chứng minh rằng
FAD  OFC và 2 OC  . OD OM . A E F H M B C D O Trang 2
Do tứ giác CDEF nội tiếp  FAD  FCD   1
Do tam giác BFC vuuong tại F  OF  OC  FCD  OFC 2 Từ  
1 và  2 suy ra  FAD  OFC
Ta có: ODF  FBD  BFD  ABC  ACB ( Do tứ giác CDFA nội tiếp) 3
BFO  FBO  ABC (Do OF  OB) Lại có: 
M FB  ACB
 MFO  BFO  MFB  ABC  ACB 4
Từ 3 và 4 ODF  M FO , kết hợp với góc FOD  FOM suy ra tam giác OFD đồng dạng với tam OM OF giác OMF 2 2    .
OD OM  OF  OC . OF OD
c)Chứng minh rằng hai đường thẳng MH và AO vuông góc với nhau. A I E F H M B D C O
Kẻ HI  MA I  MA , khi đó 5 điểm A , E , H , F , I cùng thuộc một đường tròn, suy ra:
MI.MA  M F.ME , đồng thời M F.ME  M .
B MC ( do tứ giác CBFE là tứ giác nội tiếp)
MI.MA  M . B MC .
Ta sẽ chứng minh: M . B MC  M . D MO , thật vậy: M . B MC  M .
D MO  OM  OB.OM  OC   OM  OD.OM 2 2 2
 OM  OC  OM  O . D OM 2  OC  O .
D OM ( luôn đúng theo câu b)
Từ đó suy ra MI.MA  M .
D MO  AIDO là tứ giác nội tiếp  OIA  ADO  90  OI  AM
 H ,O, I thẳng hàng, suy ra H là trực tâm tam giác AMO  MH  AO .  2  x  
1 2y  1  4
Câu 5 ( 0,5 điểm). Giải hệ phương trình  2 2 2 2
x y 1  y x 1  x y 1  2 2 Từ phương trình 2 2 2 2
x y 1  y x 1  x y 1 suy ra  2 2
x y   y x     2 2 1 1 x y   1 2  x  2
y    xy  2 x    2 y   2  y  2 x   4 4 2 2 1 2 1 . 1
1  x y  2.x y 1 2 2
 x y  xy   2 2  x y  4 4 2 2 2 4 3
 x y  2x y 1, do  2 x   2 1 y   1  2 2 2 2
4  x  y  3  x y 4 4 2 2
 x y  3.x y  4xy  2  0 . Trang 3    Đặ t 1 0
t t  xy , ta có: 4 2
t  3t  4t  2  0  t   3 2
1 t  t  2t  2  0   3 2
t  t  2t  2  0 x  1   xy   y  1 Với t  1  1    x  y  0 x 1  y  1  Với 3 2
t  t  2t  2  0 3 2
 t  t  2t  2   * Từ   2 x   2 4 1 y  
1  4  2 x .2 y  xy  1  1   xy 1 1   t 1 3 t  1  Với 1   t 1   t   2t  2   t  2 2 1 1  1 3 t  1  Khi đó,   *   ( không xảy ra)  t   2 1  0 x  1 x  1
Thử lại ta thấy hệ phương trình đã cho có nghiệm là  hoặc  .  y  1 y  1  Trang 4