



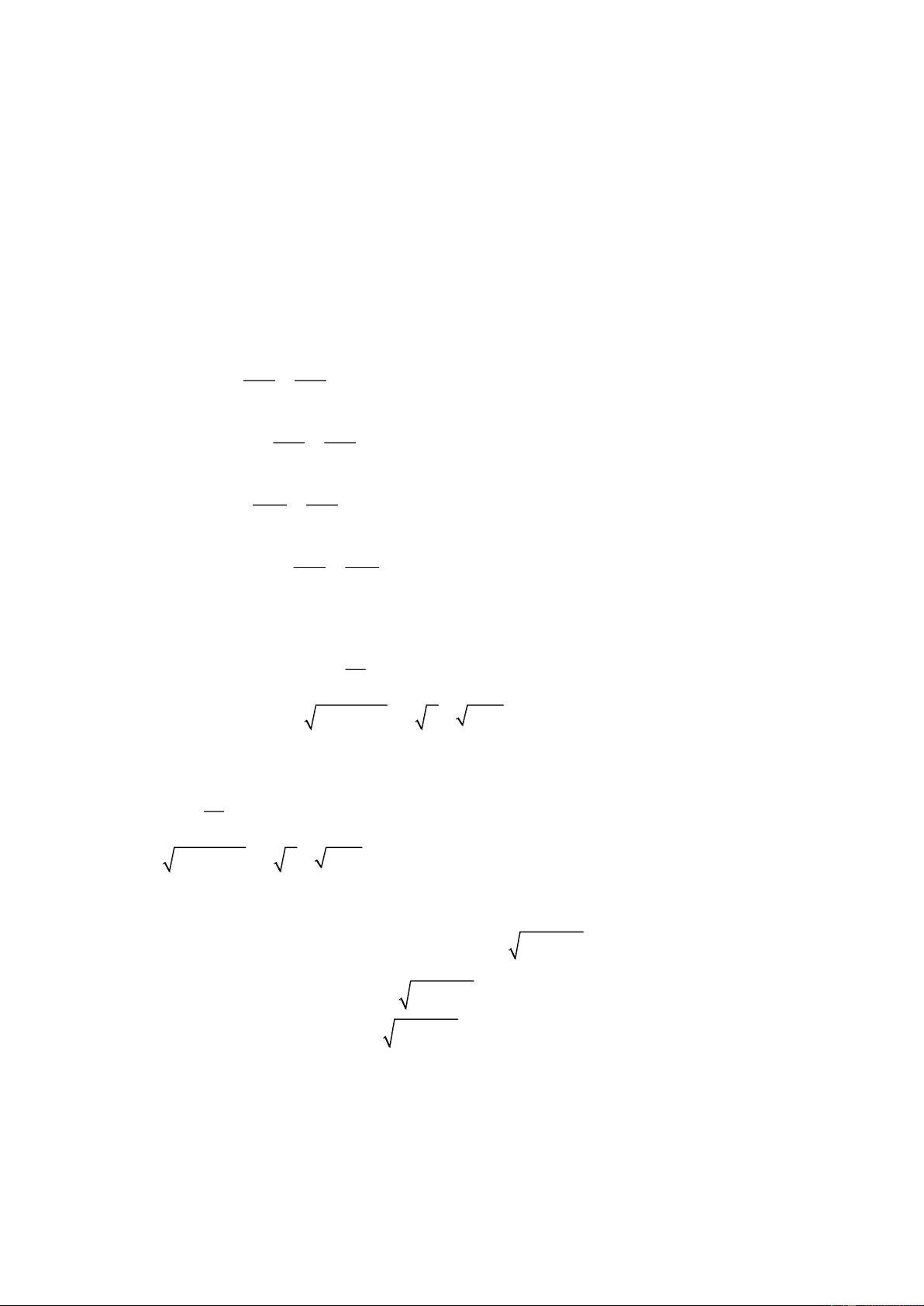

Preview text:
SỞ GIÁO DỤC ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 SƠN LA
NĂM HỌC: 2023 – 2024
Môn: TOÁN (chung)
Khoá thi ngày: 06/6/2023
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
I. Trắc nghiệm (2,0 điểm) Câu 1: Căn bậc ba của 27 là A. 9 . B. 3 . C. 9 . D. 3 . Câu 2:
Tất cả các giá trị của x để biểu thức P
x 2 có nghĩa là A. x 2 . B. x 2 . C. x 2 . D. x 2 . Câu 3:
Hàm số y mx 2 đồng biến trên khi A. m 0. B. m 0 . C. m 0 . D. m 0 . Câu 4: Đồ thị hàm số 2
y 3x đi qua điểm nào dưới đây?
A. M 0;0 .
B. N 1;6 . C. P 1 ;1 .
D. Q 0;3 . x y 4 Câu 5:
Nghiệm của hệ phương trình là
x 2y 5 A. 1; 4 . B. 1;3 . C. 1; 3 . D. 3; 1 . Câu 6: Nếu phương trình 2
ax bx c 0 với a 0 có hai nghiệm x và x , thì tích x x bằng 1 2 1 2 b c A. c . B. . C. . D. b . a a a a Câu 7:
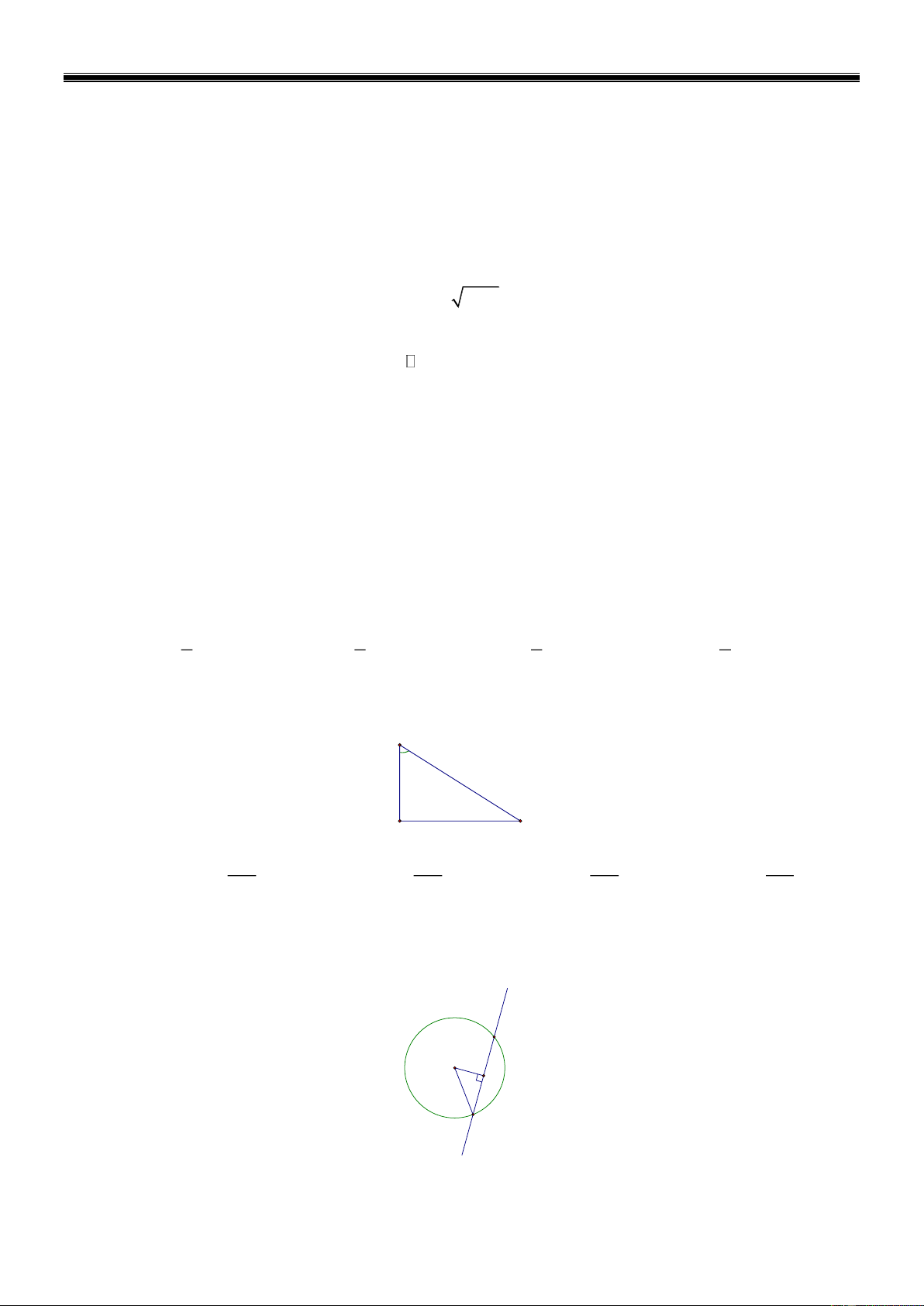
Cho tam giác ABC vuông tại A (tham khảo hình vẽ). Khẳng định nào sau đây là đúng? B A C A. cos AC B . B. cos AC B . C. cos AB B . D. cos AB B . AB BC AC BC Câu 8: Cho đường tròn ;
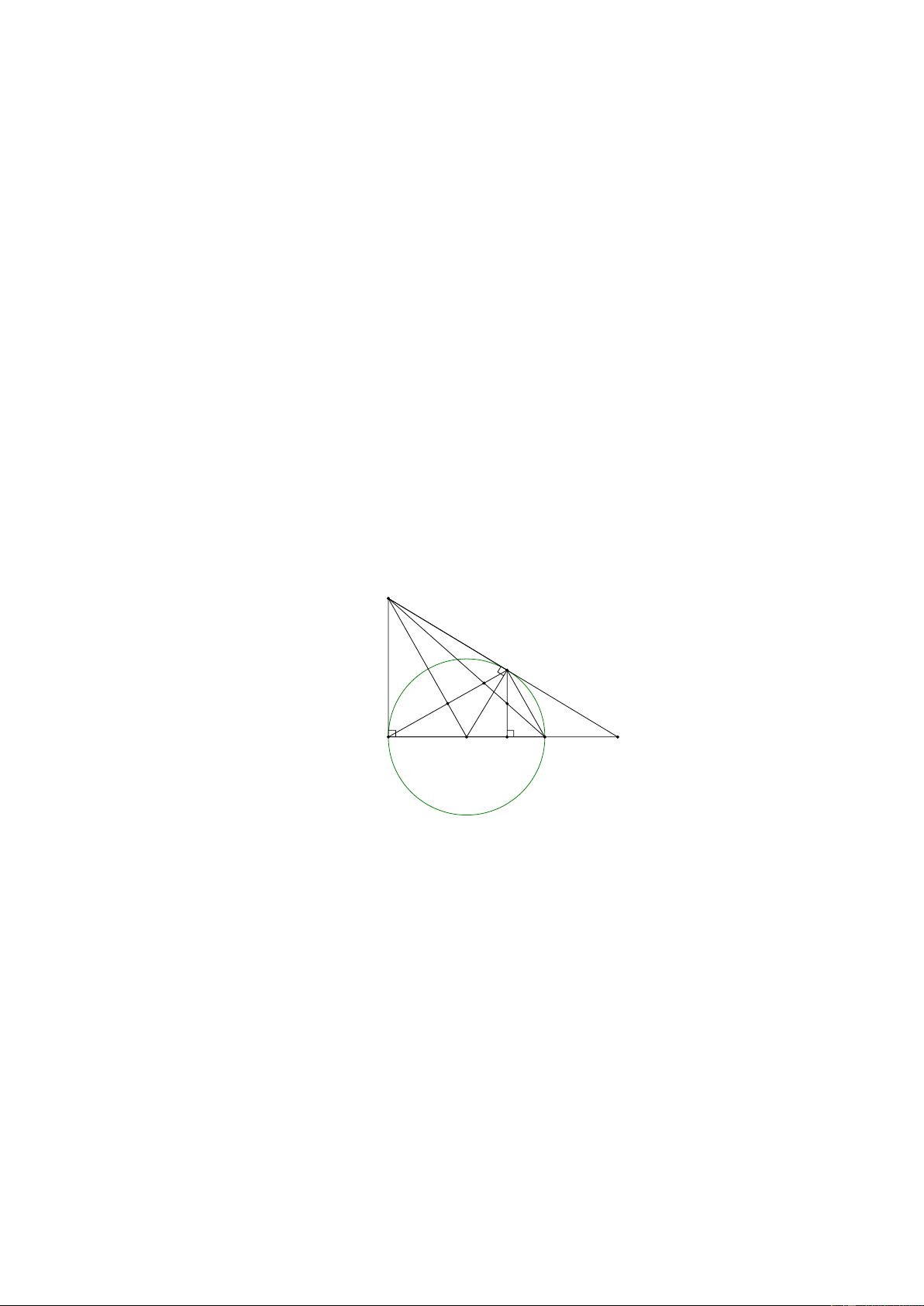
O R và đường thẳng d . Gọi H là hình chiếu vuông góc của O trên đường
thẳng d (tham khảo hình vẽ) d B O H R A
Đường thẳng d cắt ;
O R tại hai điểm phân biệt A , B khi
A. OH R .
B. OH R .
C. OH R .
D. OH R . Trang 1 Câu 9:
Số đo góc nội tiếp chắn cung 0 150 bằng A. 0 150 . B. 0 65 . C. 0 50 . D. 0 75 .
Câu 10: Công thức tính diện tích của hình cầu có bán kính R là
A. S 4 R . B. 2 S 4 R . C. 2 S R . D. 2 S 3 R .
II. Tự luận (8,0 điểm) Câu 1.
(1,5 điểm) Giải các phương trình và hệ phương trình sau:
a) 2x 8 0 b) 2
x 4x 3 0
x 2y 1 c) 3
x 2y 11 Câu 2. (1,0 điểm)
a) Tính giá trị của biểu thức: B 36 4 25 .
b) Vẽ đồ thị hàm số: y 3x 6 . Câu 3. (1,0 điểm) Cho phương trình 2
x m 2 2
1 x m 3 0 ( m là tham số). Tìm m để phương trình đã cho
có hai nghiệm phân biệt x , x thoả mãn x x x x 2 . 1 2 1 2 1 2 Câu 4. (1,0 điểm)
Ông Nam sở hữu một mảnh đất hình chữ nhật có chu vi 60 m . Ông Nam định bán mảnh đất với
giá thị trường là 8 triệu đồng cho một mét vuông. Hãy xác định giá tiền của mảnh đất đó biết rằng mảnh
đất có chiều dài gấp hai lần chiều rộng. Câu 5. (3,0 điểm)
Cho đường tròn tâm O đường kính AB . Trên đường tròn O lấy điểm C không trùng với B
sao cho AC BC . Các tiếp tuyến của đường tròn O tại A và C cắt nhau tại D . Gọi H là hình chiếu
vuông góc của C trên AB , E là giao điểm của hai đường thẳng OD và AC .
a) Chứng minh tứ giác AOCD nội tiếp.
b) Gọi F là giao điểm của hai đường thẳng CD và AB . Chứng minh CB là tia phân giác của HCF . c) Chứng minh 2 A . O AH 2AE .
d) Gọi M là giao điểm của hai đường thẳng BD và CH . Chứng minh M là trung điểm của CH . Câu 6. (0,5 điểm) 4 2 x 1 12 2
Giải hệ phương trình y .
2 x3y 2 3 y x2
-------------------------------@Hết@----------------------------------- HƯỚNG DẪN GIẢI
I. Trắc nghiệm (2,0 điểm) Câu 1: Căn bậc ba của 27 là A. 9 . B. 3 . C. 9 . D. 3 . Lời giải Trang 2 Ta có 3 3 3 27 3 3 Câu 2:
Tất cả các giá trị của x để biểu thức P
x 2 có nghĩa là A. x 2 . B. x 2 . C. x 2 . D. x 2 . Lời giải P
x 2 có nghĩa x 2 0 x 2 Câu 3:
Hàm số y mx 2 đồng biến trên khi A. m 0. B. m 0 . C. m 0 . D. m 0 . Lời giải
Hàm số y mx 2 đồng biến trên khi m 0 Câu 4: Đồ thị hàm số 2
y 3x đi qua điểm nào dưới đây?
A. M 0;0 .
B. N 1;6 . C. P 1 ;1 .
D. Q 0;3 . Lời giải Ta có 2 0 3.0 , 2 6 3.1 , 2 1 3.1 , 2
3 3.0 nên đồ thị hàm số 2
y 3x đi qua điểm M 0;0 x y 4 Câu 5:
Nghiệm của hệ phương trình là
x 2y 5 A. 1; 4 . B. 1;3 . C. 1; 3 . D. 3; 1 . Lời giải x y 4
2x 2y 8 3 x 3 x 1 Ta có
x 2y 5
x 2y 5 x y 4 y 3 Câu 6: Nếu phương trình 2
ax bx c 0 với a 0 có hai nghiệm x và x , thì tích x x bằng 1 2 1 2 b c A. c . B. . C. . D. b . a a a a Lời giải Nếu phương trình 2
ax bx c 0 với a 0 có hai nghiệm x và x , thì theo hệ thức Viét ta 1 2 có c x x 1 2 a Câu 7:
Cho tam giác ABC vuông tại A (tham khảo hình vẽ). Khẳng định nào sau đây là đúng? B A C A. cos AC B . B. cos AC B . C. cos AB B . D. cos AB B . AB BC AC BC Lời giải Ta có cos AB B BC Trang 3 Câu 8: Cho đường tròn ;
O R và đường thẳng d . Gọi H là hình chiếu vuông góc của O trên đường
thẳng d (tham khảo hình vẽ) d B O H R A
Đường thẳng d cắt ;
O R tại hai điểm phân biệt A , B khi
A. OH R .
B. OH R .
C. OH R .
D. OH R . Lời giải
Ta có OH , OA lần lượt là đường vuông góc và đường xiên kẻ từ O đến đường thẳng d nên
OH OA (quan hệ giữa đường vuông góc và đường xiên) hay OH R . Câu 9:
Số đo góc nội tiếp chắn cung 0 150 bằng A. 0 150 . B. 0 65 . C. 0 50 . D. 0 75 . Lời giải
Ta có trong một đường tròn góc nội tiếp có số đo bằng nửa số đo cung bị chắn nên số đo góc nội tiếp chắn cung 0 150 bằng 0 75 .
Câu 10: Công thức tính diện tích của hình cầu có bán kính R là
A. S 4 R . B. 2 S 4 R . C. 2 S R . D. 2 S 3 R . Lời giải Ta có 2 S 4 R .
II. Tự luận (8,0 điểm) Câu 1.
(1,5 điểm) Giải các phương trình và hệ phương trình sau:
a) 2x 8 0 b) 2
x 4x 3 0
x 2y 1 c) 3
x 2y 11 Lời giải
a) 2x 8 0 2x 8 x 4
Vậy tập nghiệm của phương trình là S 4 . b) 2
x 4x 3 0
Ta có a b c 1 4 3 0 nên phương trình đã cho có hai nghiệm phân biệt x 1 và 1 c x 3 2 a
Vậy tập nghiệm của phương trình là S 1 ; 3 . x 2y 1 4x 12 x 3 c) 3
x 2y 11 x 2y 1 y 1 Trang 4 x 3
Vậy nghiệm của hệ phương trình là . y 1 Câu 2. (1,0 điểm)
a) Tính giá trị của biểu thức: B 36 4 25 .
b) Vẽ đồ thị hàm số: y 3x 6 . Lời giải
a) Ta có B 36 4 25 6 2 5 3.
b) Vẽ hệ trục toạ độ Oxy
Cho x 0 y 3.0 6 6
đồ thị hàm số y 3x 6 đi qua điểm A0;6
Cho y 0 0 3.x 6 x 2 đồ thị hàm số y 3x 6 đi qua điểm B 2;0
Vẽ đường thẳng d đi qua hai điểm A và B ta được đồ thị hàm số y 3x 6 . Câu 3. (1,0 điểm) Cho phương trình 2
x m 2 2
1 x m 3 0 ( m là tham số). Tìm m để phương trình đã cho
có hai nghiệm phân biệt x , x thoả mãn x x x x 2 . 1 2 1 2 1 2 Lời giải
Phương trình đã cho có hai nghiệ 2
m phân biệt x , x '
m 2 0 1 1. m 3 0 1 2 2 2
m 2m 1 m 3 0 2 m 4 0 2 m 4 m 2 .
x x 2m 2
Theo hệ thức Viét ta có: 1 2 2 x x m 3 1 2
Ta có x x x x 2 2 2
2m 2 m 3 2 m 2m 3 0 (1) 1 2 1 2
Vì a b c 1 2 3 0 nên phương trình (1) có hai nghiệm phân biệt m 1 (thoả mãn) và 1 m 3 (loại) 2 Vậy m 1
là giá trị cần tìm. Câu 4. (1,0 điểm)
Ông Nam sở hữu một mảnh đất hình chữ nhật có chu vi 60 m . Ông Nam định bán mảnh đất với
giá thị trường là 8 triệu đồng cho một mét vuông. Hãy xác định giá tiền của mảnh đất đó biết rằng mảnh
đất có chiều dài gấp hai lần chiều rộng. Lời giải
Gọi chiều rộng của mảnh đất là x m (điều kiện x 0 )
Chiều dài của mảnh đất là: 2x m Trang 5
Vì chu vi của mảnh đất là 60 m nên ta có phương trình:
2 x 2x 60 3x 30 x 10m (thoả mãn điều kiện)
Diện tích mảnh đất là: 2 10.20 200 m
Giá tiền bán mảnh đất đó là: 200.8 1600 (triệu đồng) 1, 6 (tỉ đồng)
Vậy giá tiền của mảnh đất đó là 1, 6 (tỉ đồng). Câu 5. (3,0 điểm)
Cho đường tròn tâm O đường kính AB . Trên đường tròn O lấy điểm C không trùng với B
sao cho AC BC . Các tiếp tuyến của đường tròn O tại A và C cắt nhau tại D . Gọi H là hình chiếu
vuông góc của C trên AB , E là giao điểm của hai đường thẳng OD và AC .
a) Chứng minh tứ giác AOCD nội tiếp.
b) Gọi F là giao điểm của hai đường thẳng CD và AB . Chứng minh CB là tia phân giác của HCF . c) Chứng minh 2 A . O AH 2AE .
d) Gọi M là giao điểm của hai đường thẳng BD và CH . Chứng minh M là trung điểm của CH . Lời giải D C K E M A B F O H
a) Chứng minh tứ giác AOCD nội tiếp.
Ta có DA và DC là hai tiếp tuyến của O nên 0
DAO DCO 90 (tính chất của tiếp tuyến)
Xét tứ giác AOCD có 0 0 0
DAO DCO 90 90 180 mà DAO và DCO là hai góc đối nhau nên
tứ giác AOCD nội tiếp.
b) Chứng minh CB là tia phân giác của HCF . Xét O ta có 0
ACB 90 (góc nội tiếp chắn nửa đường tròn) 0
ACH BCH 90 Mà 0
ACH CAH 90 (vì ACH vuông tại H ) nên ta có BCH CAH
Lại có CAH BCF (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn CB ) nên
BCH BCF CB là tia phân giác của HCF . c) Chứng minh 2 A .
O AH 2AE . Trang 6 DA DC
Theo tính chất hai tiếp tuyến cắt nhau ta có
DO là đường trung trực của AC OA OC 2 2
AC 2AE AC 4AE (1)
Áp dụng hệ thức lượng trong tam giác vuông ABC , ta có 2 2 A .
B AH AC 2A .
O AH AC (Vì
AB 2AO ) (2) Từ (1) và (2) ta suy ra 2 2A . O AH 4AE 2 . AO AH 2AE .
d) Chứng minh M là trung điểm của CH .
Gọi K là giao điểm của AC và BD .
Vì CB là tia phân giác của HCF mà HCF là góc ngoài của DCM nên CB là phân giác ngoài BM CM của DCM
(tính chất đường phân giác trong tam giác) BD CD BM CM
Mà CD AD nên (3) BD AD HM BM
Vì CH //AD nên (định lý Talet) (4) AD BD CM HM Từ (3) và (4) ta suy ra
CM HM M là trung điểm của CH . AD AD Câu 6. (0,5 điểm) 4 2 x 1 12 2
Giải hệ phương trình y .
2 x3y 2 3 y x2 Lời giải 4 2 x 1 12 1 2 y
2 x3y 2 3 y x2 2 Điều kiện x 2 ; y 0
Phương trình 2 4 x 3y 2 9y x 2 6 y x 2
3x 3y 6 6 y x 2
x y 2 2 y x 2 x 2 2 y 4 y x 2 2 2
x 2 2 y x 2 y 4 y x 2
x 22 2yx 2 2 y 0 x 2 2 y 0
y x 2 Trang 7 4 2 2
Thay y x 2 vào 1 ta được 2 2 x 1
12 x x 2 2
4x 12 x 2 2 x 2 4 3 2 2 4 3 2
x 4x 8x 12x 48x 48 x 4x 4x 48x 48 0
x x x x x x x 2 2 2 2 2 2 4 6 12 0 2 4
3 3 0 x 2x 4 0
x 1 5 hoặc x 1 5 (thoả mãn)
Với x 1 5 y 3 5 (thoả mãn)
Với x 1 5 y 3 5 (thoả mãn) x 1 5 x 1 5
Vậy hệ phương trình có hai nghiệm phân biệt và . y 3 5 y 3 5 Trang 8




