Đề thi tuyển sinh vào lớp 10 năm 2023-2024 môn toán không chuyên Sở GD Tây Ninh (có đáp án và lời giải chi tiết)

SỞ GIÁO DỤC VÀ ĐÀO TẠO TÂY NINH.
KỲ THI TUYỂN SINH LỚP 10 NĂM HỌC 2023 – 2024 ĐỀ CHÍNH THỨC
Ngày thi: 02 tháng 06 năm 2023
(Đề thi có 1 trang, thí sinh không phải chép đề vào giấy
Môn thi: TOÁN (không chuyên) thi)
Thời gian: 120 phút (Không kể thời gian giao đề) 2
Câu 1. (1,0 điểm) Tính giá trị của biểu thức P = 4 + ( 2) .
Câu 2. (1,0 điểm) Giải phương trình 2
x - 5x + 6 = 0 . ìï x - y = 5 ï
Câu 3. (1,0 điểm) Giải hệ phương trình í . ï 2x + y = 4 ïî
Câu 4. (1,0 điểm) Vẽ đồ thị của hàm số 2 y = - 2x .
Câu 5. (1,0 điểm) Cho tam giác A BC cân tại A, A B = A C = 5 và đường cao A H = 3 . Tính độ dài B C .
Câu 6. (1,0 điểm) Trong hệ trục tọa độ Oxy , cho đường thẳng (d) : y = 5x - 3 . Tìm tọa độ điểm M thuộc
(d ) biết điểm M có hoành độ bằng 4 .
Câu 7. (1,0 điểm) Cho phương trình 2
x + (m - 8)x + 3m + 9 = 0 . Tìm giá trị của m để phương trình đã
cho có hai nghiệm phân biệt x , x thỏa mãn 2 2 x + x = 25 . 1 2 1 2
Câu 8. (1,0 điểm) Hệ thống cáp treo núi Bà Đen tỉnh Tây Ninh gồm hai tuyến Vân Sơn và Chùa Hang có
tổng cộng 191 cabin, mỗi cabin có sức chứa 10 người. Nếu tất cả các cabin của hai tuyến đều chứa đủ số
người theo qui định thì số người ở tuyến Vân Sơn nhiều hơn số người ở tuyến Chùa Hang là 350 người.
Tính số cabin của mỗi tuyến.
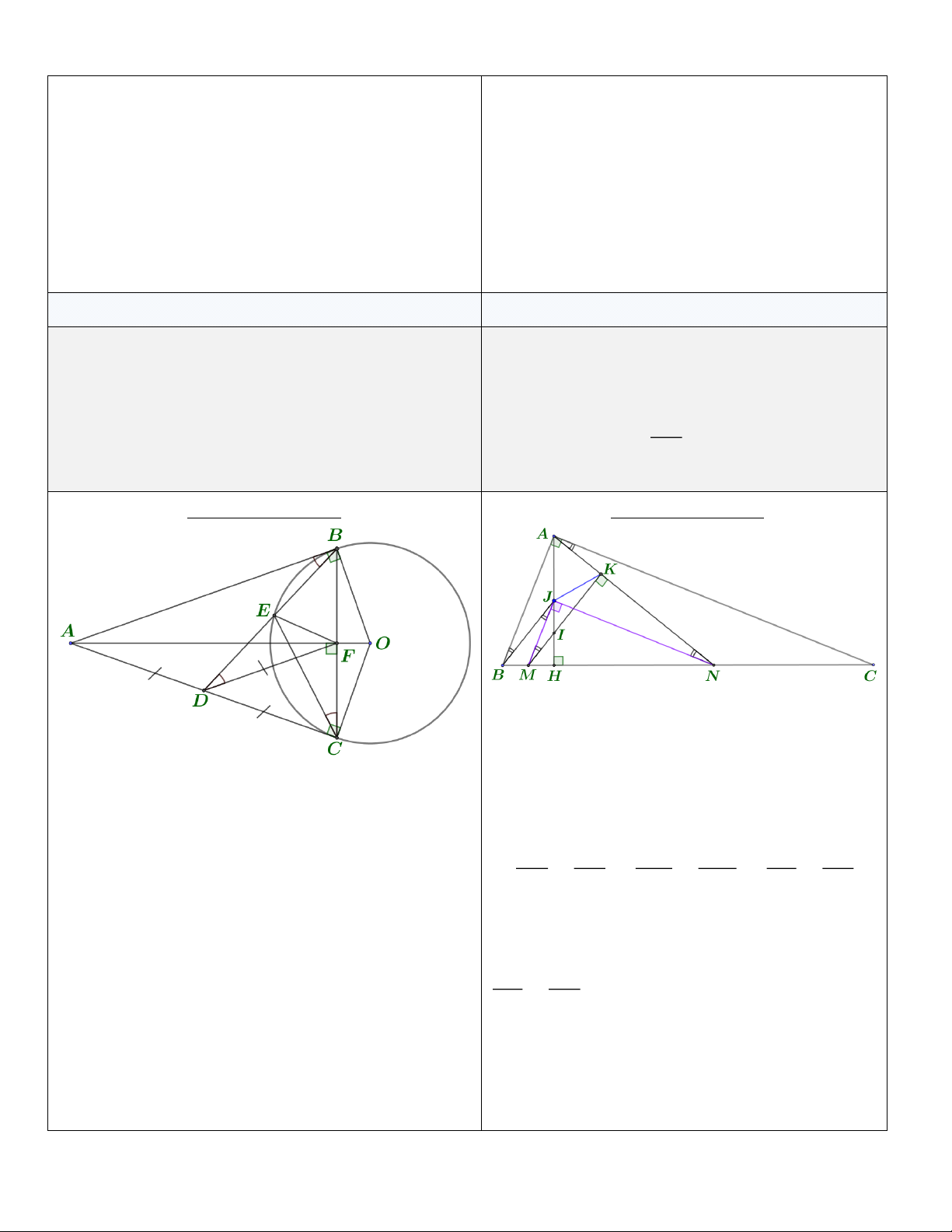
Câu 9. (1,0 điểm) Cho đường tròn (O ) và điểm A nằm ngoài (O ) . Từ A vẽ các tiếp tuyến A B, A C với
(O ) ( B và C là các tiếp điểm). Gọi D là trung điểm của đoạn thẳng A C , B D cắt (O ) tại E (khác B ) và
B C cắt OA tại F . Chứng minh bốn điểm C , D, E , F cùng thuộc một đường tròn.
Câu 10. (1,0 điểm) Cho tam giác A BC vuông tại A , đường cao A H . Gọi M , N lần lượt là trung điểm A H
của HB và HC . Kẻ MK vuông góc với A N tại K , MK cắt A H tại I . Tính . A I ---Hết--- Trang 1
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1 Câu 2 2
Tính giá trị của biểu thức x - x + = P = 4 + ( 2) . Giải phương trình 2 5 6 0 .
Lời giải tham khảo
Lời giải tham khảo 2 ▪ Ta có: 2
D = b - 4ac = 25 - 24 = 1. ▪ Ta có: P = 4 + ( 2) 2 = 2 + 2 = 2 + 2 = 4 .
▪ Phương trình có hai nghiệm phân biệt 5 + 1 5 - 1 x = = 3 ; x = = 2. 1 2.1 2 2.1 Câu 3 Câu 4 ìï x - y = 5 ï Vẽ đồ thị hàm số 2 y = - 2x . Giải hệ phương trình í ï 2x + y = 4 ïî
Lời giải tham khảo
Lời giải tham khảo ìï x - y = 5 ì ï ï 3x = 9 ï ▪ Ta có bảng giá trị: ▪ Ta có: í Û í ï 2x + y = 4 ï ï î x - y = 5 ïî x - 2 - 1 0 1 2 ìï x = 3 ìï x = 3 ï ï 2 y = - 2x Û í Û í ï - 8 - 2 0 - 2 - 8 3 - y = 5 ï y = - 2 ïî ïî
▪ Vậy hệ phương trình có nghiệm (3;- ) 2 . ▪ Đồ thị: Câu 5 Câu 6
Cho tam giác A BC cân tại A, A B = A C = 5 và
Trong hệ trục tọa độ Oxy , cho đường thẳng
đường cao A H = 3 . Tính độ dài B C .
(d) : y = 5x - 3 . Tìm tọa độ điểm M thuộc (d ) Trang 2
biết điểm M có hoành độ bằng 4 .
Lời giải tham khảo
Lời giải tham khảo
▪ Do điểm M thuộc (d ) biết điểm M có hoành
độ bằng 4 nên thay x = 4 vào y = 5x - 3 ta được:
y = 5.4 - 3 = 20 - 3 = 17 . ▪ Suy ra: M (4;17). µ
▪ Xét DA BH (H = 90 ) ° ta có: 2 2 2
A B = A H + BH (định lí Pytago) 2 2 2 2 Þ BH = A B - A H = 5 - 3 = 4
▪ Do DA BC cân tại A và A H là đường cao nên
A H cũng là trung tuyến Þ BC = 2BH = 2.4 = 8 . Câu 7 Câu 8 Cho phương trình 2
x + (m - 8)x + 3m + 9 = 0 .
Hệ thống cáp treo núi Bà Đen tỉnh Tây Ninh
Tìm giá trị của m để phương trình đã cho có hai
gồm hai tuyến Vân Sơn và Chùa Hang có tổng
nghiệm phân biệt x , x thỏa mãn 2 2 x + x = 25 .
cộng 191 cabin, mỗi cabin có sức chứa 10 người. 1 2 1 2
Nếu tất cả các cabin của hai tuyến đều chứa đủ
số người theo qui định thì số người ở tuyến Vân
Sơn nhiều hơn số người ở tuyến Chùa Hang là
350 người. Tính số cabin của mỗi tuyến.
Lời giải tham khảo
Lời giải tham khảo ▪ Xét phương trình: 2
x + (m - 8)x + 3m + 9 = 0
▪ Gọi x ;y lần lượt là số cabin tuyến Vân Sơn và
▪ Để phương trình có hai nghiệm phân biệt thì
Chùa Hang (x ;y nguyên dương) D = (m - )2 8 - 4.1.(3m + 9)
▪ Do tổng cộng có 191 cabin nên: 2
= m - 16m + 64 - 12m - 36 2
= m - 28m + 28 > 0 x + y = 191 ( ) 1 ▪ Theo hệ thức vi-ét:
▪ Do tất cả các cabin của hai tuyến đều chứa đủ b
số người theo qui định thì số người ở tuyến Vân x + x = -
= - m - 8 = 8 - m và 1 2 ( ) ( ) a
Sơn nhiều hơn số người ở tuyến Chùa Hang là c 10x - 10y = 350 2 x .x = = 3m + 9 350 người nên ta có: ( ) 1 2 a ▪ Từ ( )
1 và (2) ta có hệ phương trình: ▪ Ta có: 2 2
x + x = 25 Û (x + x - 2x x = 25 1 2 )2 1 2 1 2 ìï x + y = 191 ì ï
ï 10x + 10y = 1910 ï Û ( - í Û í m )2 8 - 2(3m + 9) = 25
ï 10x - 10y = 350 ï ï î 10x - 10y = 350 ïî 2
Û 64 - 16m + m - 6m - 18 = 25 Trang 3 m é = 1 ìï 20x = 2260 ìï x = 113 2 Û ï ï m - 22m + 21 = 0 ê Û Û í Û í m ê = 21 ê ï + = ï ë x y 191 y = 191 - 113 = 78 ïî ïî ▪ Với m = 1 thì 2 D = 1 - 28.1 + 28 = 1 > 0.
▪ Vậy số cabin của tuyến Vân Sơn là 113 và số
Suy ra nhận giá trị m = 1
cabin của tuyến Chùa Hang là 78 . ▪ Với m = 21 thì 2
D = 21 - 28.21 + 28 = - 119 < 0 .
Suy ra loại giá trị m = 21 .
Vậy m = 1 là giá trị cần tìm. Câu 9 Câu 10
Cho đường tròn (O ) và điểm A nằm ngoài (O ) . Từ Cho tam giác A BC vuông tại A , đường cao
A vẽ các tiếp tuyến A B , A C với (O ) ( B và C là
A H . Gọi M , N lần lượt là trung điểm của HB
các tiếp điểm). Gọi D là trung điểm của đoạn thẳng
và HC . Kẻ MK vuông góc với A N tại K , MK
A C , B D cắt (O ) tại E (khác B ) và B C cắt OA tại A H
cắt A H tại I . Tính .
F . Chứng minh bốn điểm C , D, E , F cùng thuộc A I một đường tròn.
Lời giải tham khảo
Lời giải tham khảo
▪ Gọi J là trung điểm của A H .
▪ Xét DA BH và DCA H có: · ·
A HB = A HC = 90°
▪ Theo tính chất hai tiếp tuyến cắt nhau thì · · ·
A B = A C ;OB = OC Þ A O là trung trực của B C
A B H = CA H (cùng phụ với A CB )
hay F là trung điểm B C .
Þ DA BH ~ DCA H (g - g)
▪ Xét DA BC có: A D = DC ;BF = FC Þ DF là A B A C A B A C A B A C Þ = Þ = Þ = · · A H CH 2A J 2CN A J CN
đường trung bình DA BC Þ A BD = BDF (so le
▪ Xét D A BJ và DCA N có: trong). · · · · · »
B A J = A CN (cùng phụ với A BC )
▪ Mặt khác: A BD = ECF (cùng chắn EB ). · · A B A C
▪ Suy ra: EDF = ECF . = (cmt ) A J CN
▪ Vậy tứ giác DEFC nội tiếp đường tròn (vì có đỉnh · ·
Þ DA BJ ~ DCA N Þ A BJ = CA N (1)
D,C cùng nhìn cạnh EF dưới một góc không đổi).
▪ Ta có: MJ là đường trung bình DHA B · ·
Þ MJ / / A B Þ A BJ = BJM (2) (so le trong) Trang 4
▪ Tương tự: JN là đường trung bình DA HC · ·
Þ JN / / A C Þ CA N = A NJ (3) (so le trong) ìï MJ / / A B ïïï ·
▪ Ta có: í IN / / A C Þ MJ ^ JN Þ MJN = 90° ï ïï AB ^ AG ïïî
▪ Xét tứ giác MJKN có: · ·
MJN = MKN = 90° Þ MJKN nội tiếp (hai
cạnh kề nhau cùnh nhìn MN dưới góc vuông) · · Þ »
A NJ = JMK (góc nội tiếp chắn JK ) (4) ▪ Từ ( ) 1 ,( ) 2 ,( ) 3 ,(4) · ·
Þ BJM = JMK Þ BJ / / MK Þ BJ / / MI ▪ Xét D BHJ có:
M là trung điểm B H B J / / MI
Þ I là trung điểm JH 1 1 1 1 Þ IH = JH = × A H = A H 2 2 2 4 3
A I = A H - IH = A H 4 A H A H 4 ▪ Vậy = = . A I 3 3 A H 4 ---Hết--- Trang 5