
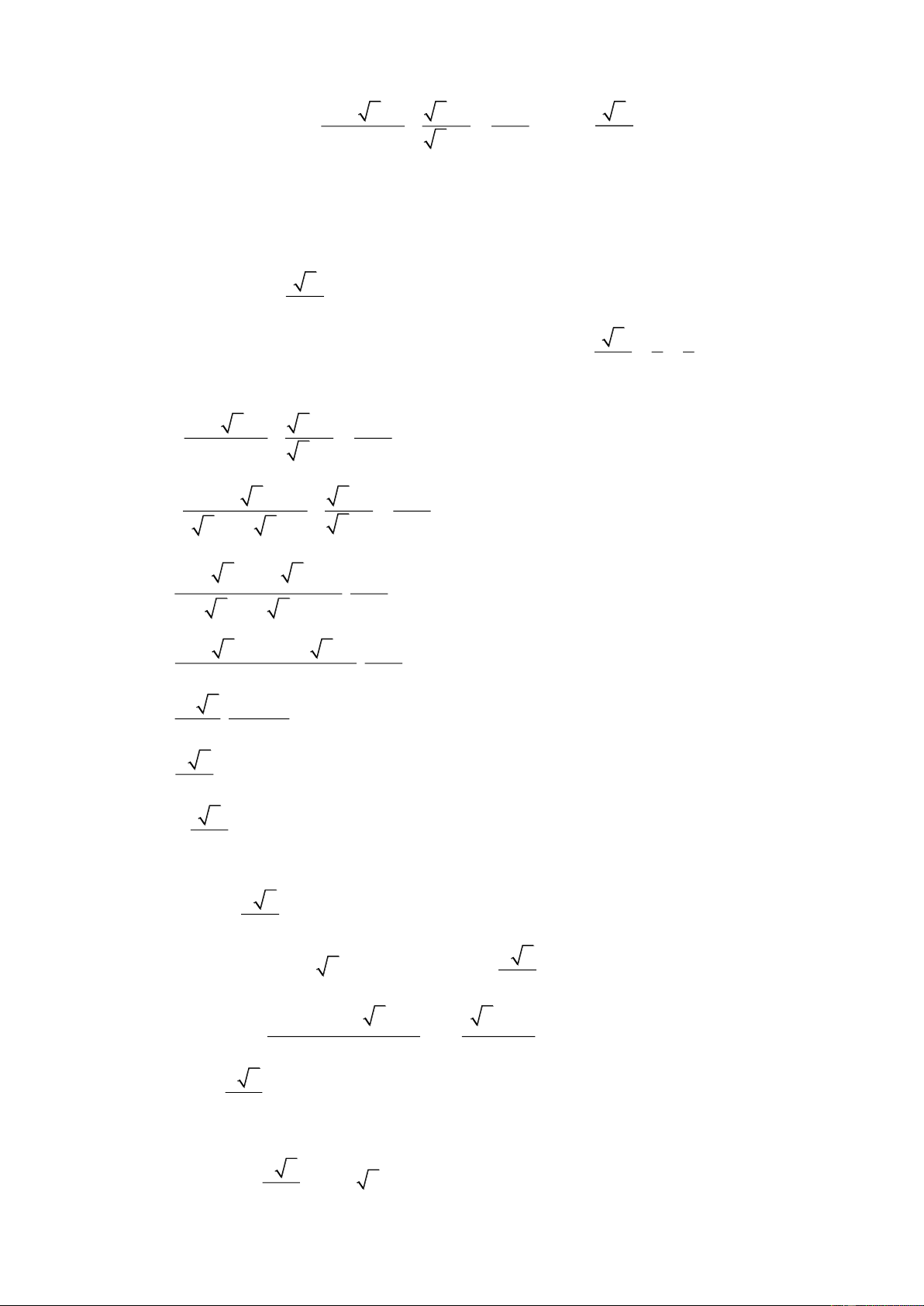
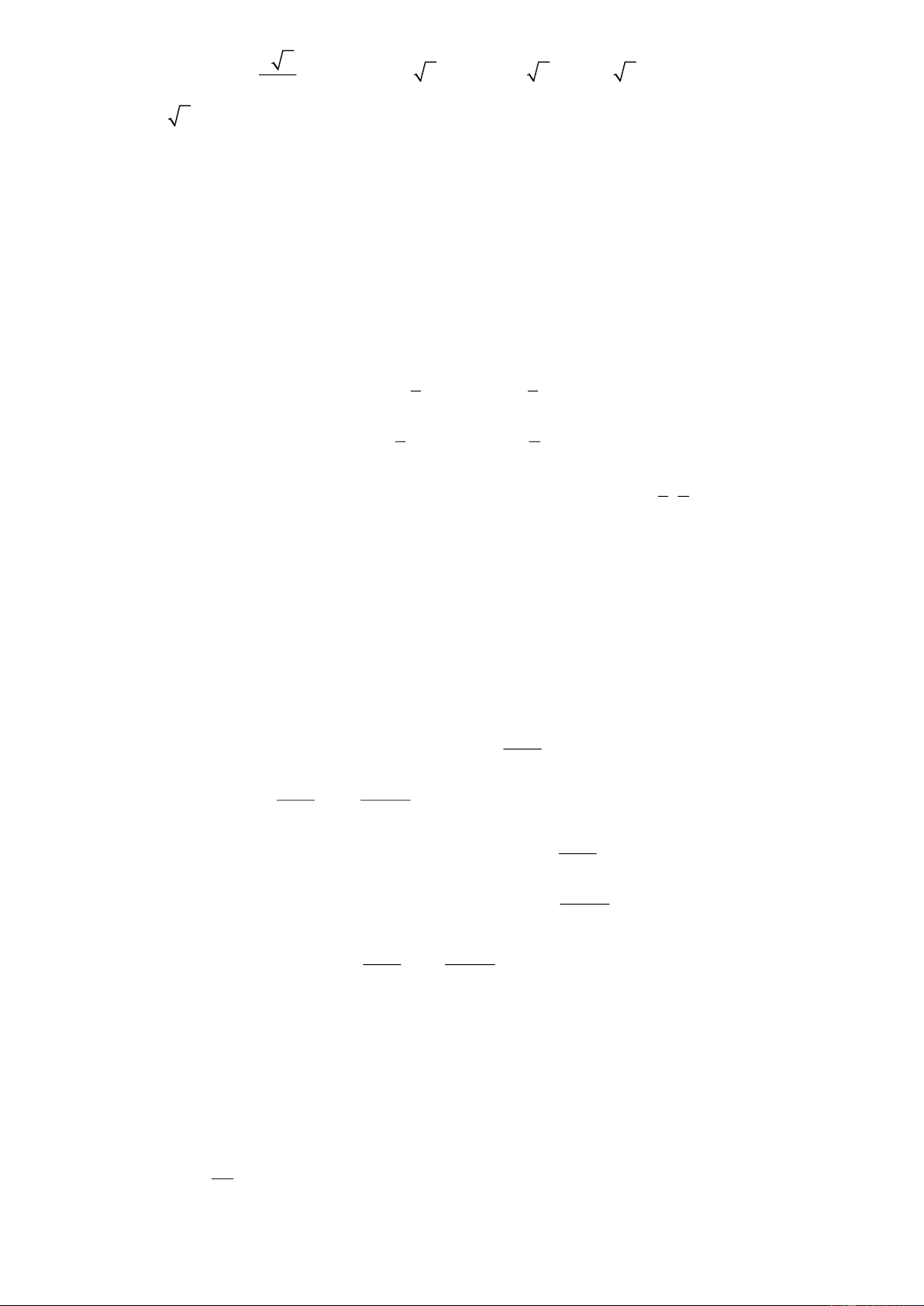

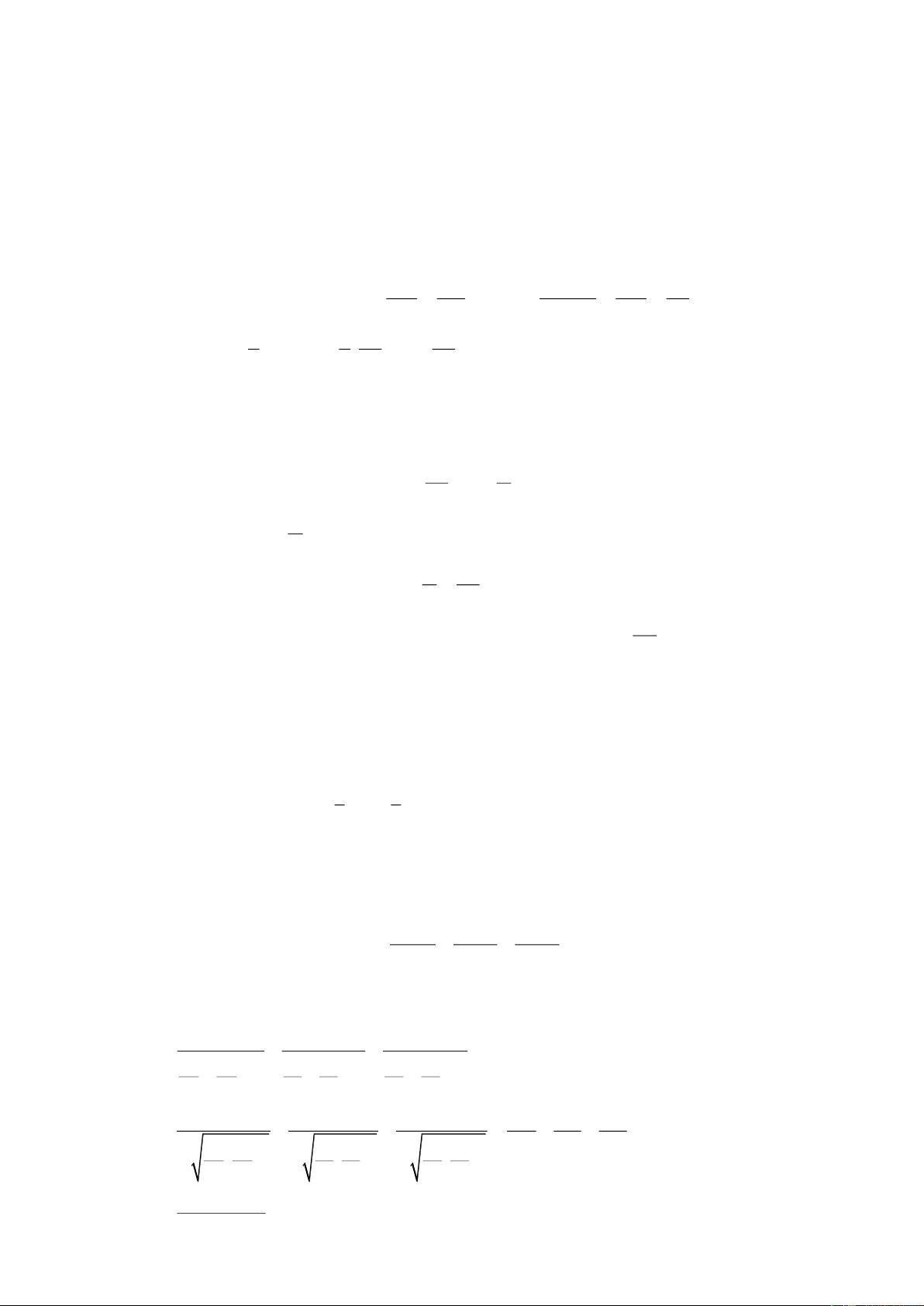

Preview text:
SỞ GIÁO DỤC ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THÁI BÌNH
NĂM HỌC: 2023 – 2024 Môn: TOÁN
Khoá thi ngày: 8/6/2023
Thời gian làm bài: 120 phút (không kể thời gian giao đề) Câu 1. (2,0 điểm)
x 6 x 1
x 1 x 4 x
Cho hai biểu thức P : và Q
(với x 0; x 1). x 1 x 1 1 x x 4
a) Tính giá trị biểu thức Q với x 4 .
b) Chứng minh rằng P 4Q .
c) Tìm tất cả các giá trị của x để P nhận giá trị là số nguyên. Câu 2. (2,0 điểm)
mx y 3 Cho hệ phương trình
(với m là tham số).
x y 2
a) Giải hệ phương trình với m 2 .
b) Tìm m để hệ phương trình có nghiệm duy nhất x; y thỏa mãn 2 2
x y 10 . Câu 3.
(2,0 điểm) Trong mặt phẳng tọa độ Oxy, cho parabol P 2
: y 2x và đường thẳng
d: y x m (với m là tham số).
a) Tìm m để d đi qua điểm A2;8 .
b) Tìm m để d cắt P tại hai điểm phân biệt có hoành độ x , x thỏa mãn: 1 2
x x 3x x 5. 1 2 1 2 Câu 4. (3,5 điểm)
b) Cho tam giác ABC nhọn, nội tiếp đường tròn O; R . Kẻ AH vuông góc với BC tại H ,
HK vuông góc với AB tại K và HI vuông góc với AC tại I .
a) Chứng minh tứ giác AKHI nội tiếp đường tròn.
b) Gọi E là giao điểm của AH với KI . Chứng minh rằng E .
A EH EK.EI .
c) Chứng minh KI vuông góc với AO .
d) Giả sử điểm A và đường tròn O; R cố định, còn dây BC thay đổi sao cho 2 A . B AC 3R .
Xác định vị trí của dây cung BC sao cho tam giác ABC có diện tích lớn nhất.
2) Một hình nón có diện tích đáy bằng 2 16
cm và có chiều cao gấp ba lần bán kính đáy.
Tính thể tích của hình nón đó. Câu 5. (0,5 điểm) Cho các số thực dương ,
x y, z thỏa mãn x y z 6. Tìm giá trị lớn nhất của biểu thức 3 3 3 xy yz zx P . 3 3 3 y 4 z 4 x 4
---------------------------------@Hết@--------------------------------- Trang 1 HƯỚNG DẪN GIẢI Câu 1. (2,0 điểm)
x 6 x 1
x 1 x 4 x
Cho hai biểu thức P : và Q
(với x 0; x 1). x 1 x 1 1 x x 4
a) Tính giá trị biểu thức Q với x 4 .
b) Chứng minh rằng P 4Q .
c) Tìm tất cả các giá trị của x để P nhận giá trị là số nguyên. Lời giải x
a) Theo bài ra Q
với x 0; x 1 x 4 4 2 1
Thay x 4 (thỏa mãn điều kiện) vào biểu thức Q ta có: Q . 4 4 8 4
b) Với x 0; x 1 ta có:
x 6 x 1
x 1 x 4 P : x 1 x 1 1 x x 6 x 1 x 1 x 4 P x 1 x : 1 x 1 1 x x
x x 2 6 1 1 1 x p x 1 x . 1 x 4
x 6 x 1 x 2 x 1 1 x P . x 1 x 4
4 x x 1 P . x 1 x 4 4 x P x 4 x P 4. 4.Q x 4
Vậy P 4Q với x 0; x 1. 4 x c) Ta có P
với x 0; x 1. x 4 4 x
Với x 0; x 1 ta có 4 x 0; x 4 0 P 0 1 x 4
x x x x 2 4 4 4 2 Ta cũng có: P 1 1 x x x 4 x với 0; 1 4 Do đó 4 x P 1 2 x 4 Từ
1 và 2 0 P 1. Mà P nhận giá trị là số nguyên nên P 0; 1 . x + Với P 4 0
0 x 0 x 0 (thỏa mãn) x 4 Trang 2 x + Với P 1 x x x x x 2 4 1 4 4 4 4 0 2 0 x 4
x 2 0 x 4 (thỏa mãn). Vậy x 0;
4 thì P nhận giá trị là số nguyên. Câu 2. (2,0 điểm)
mx y 3 Cho hệ phương trình
(với m là tham số).
x y 2
a) Giải hệ phương trình với m 2 .
b) Tìm m để hệ phương trình có nghiệm duy nhất x; y thỏa mãn 2 2
x y 10 . Lời giải
a) Với m 2 hệ phương trình đã cho trở thành: 1 1 x x
2x y 3 3 x 1 3 3
x y 2
x y 2 1 7 y 2 y 3 3
Vậy với m 2 hệ phương trình đã cho có nghiệm duy nhất x y 1 7 ; ; . 3 3
mx y 3 1
b) Xét hệ phương trình
x y 2 2
Từ 2 ta có y x 2 3 . Thay 3 vào
1 ta được: mx x 2 3 m 1 x 1 4
Hệ phương trình có nghiệm duy nhất khi phương trình 4 có nghiệm duy nhất
m1 0 m 1 1 Với m 1
phương trình 4 có 1 nghiệm x . m 1 1 2m 3
Từ 2 ta có y 2 . m 1 m 1 1 x m 1 Với m 1
, hệ phương trình có nghiệm duy nhất 2m 3 y m 1 2 2 1 2m 3 Theo bài ra 2 2
x y 10 10 m 1 m 1 2 2
1 2m 3 10m 1 2 2
1 4m 12m 9 10m 20m 10 2
6m 8m 0
2m3m 4 0 m 0 4 (thỏa mãn). m 3 Trang 3 4 Vậy m ; 0thỏa mãn đề bài. 3 Câu 3.
(2,0 điểm) Trong mặt phẳng tọa độ Oxy, cho parabol P 2
: y 2x và đường thẳng
d: y x m (với m là tham số).
a) Tìm m để d đi qua điểm A2;8 .
b) Tìm m để d cắt P tại hai điểm phân biệt có hoành độ x , x thỏa mãn: 1 2
x x 3x x 5. 1 2 1 2 Lời giải
a) Đường thẳng d : y x m đi qua điểm A2;8 2 m 8 m 6 .
Vậy m 6 thì d đi qua điểm A2;8 .
b) Xét phương trình hoành độ giao điểm của parabol P 2
: y 2x và đường thẳng
d: y x m là: 2 2
2x x m 2x x m 0 * . Phương trình 2 * có:
1 4.2.m 1 8m .
Để d cắt P tại hai điểm phân biệt có hoành độ x , x thì phương trình * có hai nghiệm 1 2 1
phân biệt x , x 0 1 8m 0 m . 1 2 8 1 x x 1 2 Theo đị 2 nh lí Vi-et ta có: m x .x 1 2 2 m
Theo bài ra: x x 3x x 1 5 3.
5 1 3m 10 3m 9 m 3(thỏa mãn). 1 2 1 2 2 2
Vậy m 3 là giá trị cần tìm. Câu 4. (3,5 điểm)
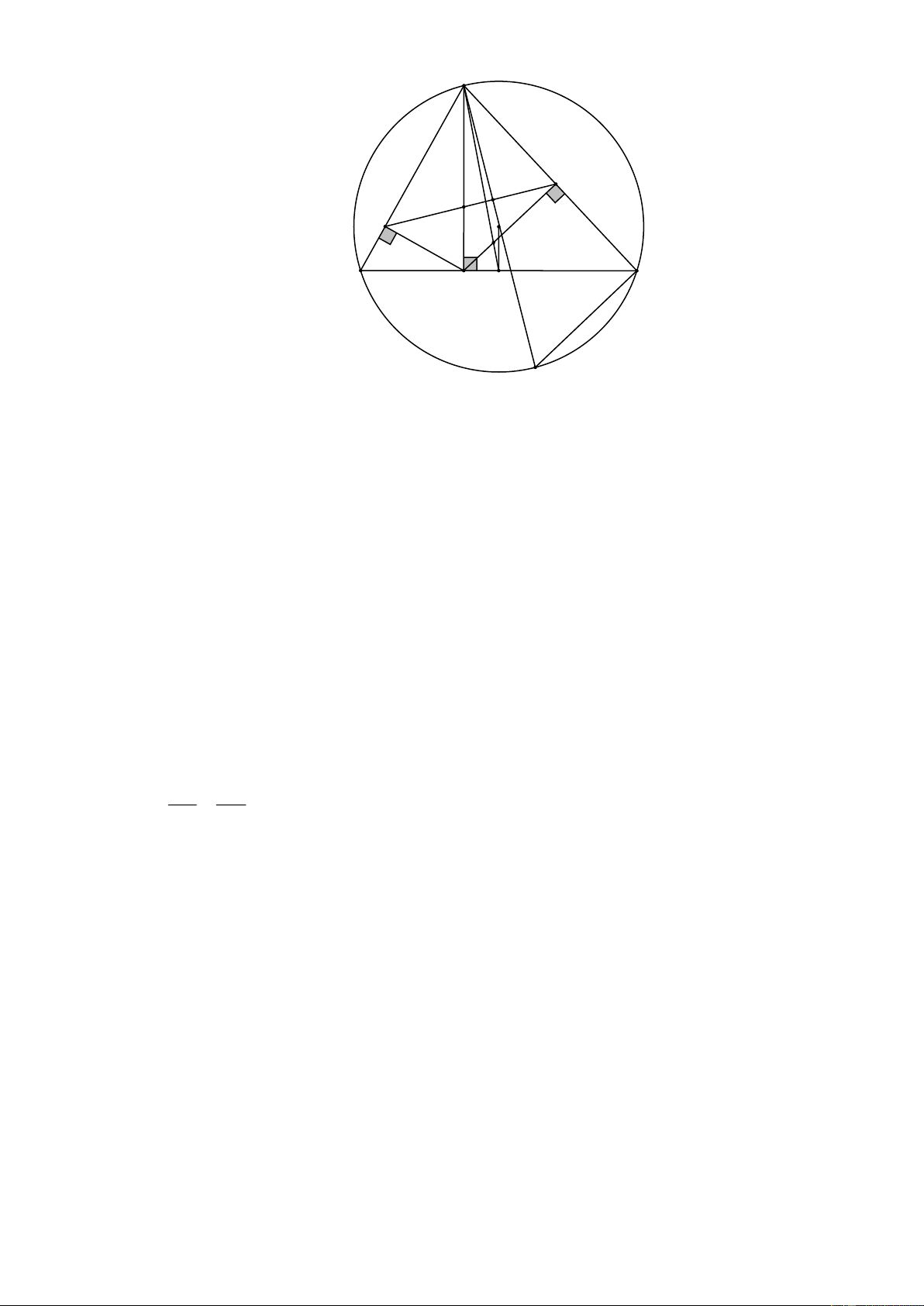
1) Cho tam giác ABC nhọn, nội tiếp đường tròn O; R . Kẻ AH vuông góc với BC tại H ,
HK vuông góc với AB tại K và HI vuông góc với AC tại I .
a) Chứng minh tứ giác AKHI nội tiếp đường tròn.
b) Gọi E là giao điểm của AH với KI . Chứng minh rằng E .
A EH EK.EI .
c) Chứng minh KI vuông góc với AO .
d) Giả sử điểm A và đường tròn O; R cố định, còn dây BC thay đổi sao cho 2 A . B AC 3R .
Xác định vị trí của dây cung BC sao cho tam giác ABC có diện tích lớn nhất.
2) Một hình nón có diện tích đáy bằng 2 16
cm và có chiều cao gấp ba lần bán kính đáy.
Tính thể tích của hình nón đó. Lời giải Trang 4 A 1 1 E J K O 1 2 B C H M 1 F
1. a) Chứng minh tứ giác AKHI nội tiếp đường tròn. Ta có:
AKH 90 (vì HK vuông góc với AB tại K )
AIH 90 (vì HI vuông góc với AC tại I ).
Xét tứ giác AKHI có: AKH AIH 90 90 180 , mà hai góc này ở vị trí đối nhau.
Vậy tứ giác AKHI nội tiếp đường tròn.
b) Gọi E là giao điểm của AH với KI . Chứng minh rằng E .
A EH EK.EI .
Vì tứ giác AKHI nội tiếp đường tròn (cmt) nên HKI HAI (hai góc nội tiếp cùng chắn HI )
Hay HKE IAE . Xét E KH và EAI có:
KEH AEI (hai góc đối đỉnh);
HKE IAE (cmt) Do đó: E KH ∽ E AI (g.g) EK EH E .
A EH EK.EI EA EI
Vậy ta có điều phải chứng minh.
c) Chứng minh KI vuông góc với AO .
Kẻ đường kính AF của đường tròn O; R . Gọi J là giao điểm của KI và AO .
Xét đường tròn O; R có F B (hai góc nội tiếp cùng chắn cung AC ). 1 1 1
Lại có B H (vì cùng phụ với H ). 2 1 1 2
Vì tứ giác AKHI nội tiếp đường tròn (cmt)
nên H I (hai góc nội tiếp cùng chắn cung AK ) 3 1 1 Từ
1 ; 2 và 3 suy ra: F I . 1 1
Mà trong đường tròn O; R có: ACF 90 (góc nội tiếp chắn nửa đường tròn).
Hay A F 90 4 . 1 1
Từ 3 và 4 suy ra A I 90 AJI 90 . 1 1
Vậy KI vuông góc với AO . Trang 5
d) Giả sử điểm A và đường tròn O; R cố định, còn dây BC thay đổi sao cho 2 A . B AC 3R .
Xác định vị trí của dây cung BC sao cho tam giác ABC có diện tích lớn nhất.
Có ACF 90 (góc nội tiếp chắn nửa đường tròn)
ABH AFC (hai góc nội tiếp cùng chắn cung AC của đường tròn O; R Xét A HB và A CF có:
AHB ACF 90 ;
ABH AFC (cmt) 2 Do đó: AH AB A . B AC 3R 3R A HB A ∽ CF (g.g) AH . AC AF AF 2R 2 1 1 3R 3R Ta có: S AH.BC . .BC .BC . ABC 2 2 2 4
Do R không đổi nên S
lớn nhất BC lớn nhất. ABC
Gọi M là trung điểm của BC thì OM BC .
BC lớn nhất OM bé nhất. 3R R
Ta có OM AM AO AH AO R . 2 2 R OM bé nhất bằng ,
A O, M thẳng hàng và H M . 2 Khi đó R 3R
AH AM AO OM R . 2 2 3R Vậy diện tích ABC
lớn nhất khi BC cách A một khoảng bằng ( ABC đều) 2
2) Gọi bán kính đáy của hình nón là R .
Do diện tích của đáy hình nón là 2
S 16 R
16 R 4cm
Theo giả thiết chiều cao của hình nón gấp 3 lần bán kính đáy nên chiều cao của hình nón là:
h 3R 3.4 12cm 1 1
Thể tích hình nón là: V S.h .16 .1 2 =64 3 cm 3 3
Vậy thể tích hình nón là 3 64 cm . Câu 5. (0,5 điểm) Cho các số thực dương ,
x y, z thỏa mãn x y z 6. Tìm giá trị lớn nhất của biểu thức 3 3 3 xy yz zx P . 3 3 3 y 4 z 4 x 4 Lời giải
Áp dụng bất đẳng thức AM – GM cho ba số dương ta có: 3 3 3 xy yz zx P 3 3 3 3 3 3 y y z z x x 4 4 4 2 2 2 2 2 2 3 3 3 3 3 3 xy yz zx xy yz zx P 2 2 2 3 3 3 3 3 3 3y 3z 3x y y z z x x 3 3 3 3. . .4 3. . .4 3. . .4 2 2 2 2 2 2
xy yz zx P . 3 Trang 6 2 2 2
Lại có x y y z z x 0 , x y, z 2 2 2
x y z xy yz zx
x y z2 3xy yz zx
x y z 2 6
xy yz zx 12 3 3 12 P 4 . 3
x y z Dấu “=” xảy ra khi
x y z 2 .
x y z 6
Vậy MaxP 4 x y z 2 .
---------------------------------@Hết@--------------------------------- Trang 7




