Đề thi tuyển sinh vào lớp 10 THPT Chuyên Hùng Vương năm học 2023-2024 môn toán Sở GD Phú Thọ (có đáp án và lời giải chi tiết)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 PHÚ THỌ
TRUNG HỌC PHỔ THÔNG CHUYÊN HÙNG VƯƠNG NĂM HỌC 2023-2024 Môn: Toán ĐỀ CHÍNH THỨC
(Dành cho thí sinh thi chuyên Toán)
Thời gian làm bài: 150 phút, không kể thời gian giao đề.
Đề thi có 01 trang
Câu 1 (2,0 điểm).
a) Tìm tất cả các giá trị của tham số m để phương trình 2
x  m   2 2
1 x  m  2m  8  0 có hai
nghiệm phân biệt x , x thỏa mãn x  6  x . 1 2 1 2 1 1
b) Cho f  x  1 
với x  0, x  1  . Tính f  
1  f 2  f 3   f 2023. 2 x x  2 1
Câu 2 (2,0 điểm).
a) Cho các số nguyên a, b, c, d thỏa mãn điều kiện 3 3 3 3
a  b  8c  28d  0.
Chứng minh rằng     2 a b c d chia hết cho 9.
b) Chứng minh rằng tồn tại đa thức P  x có hệ số thực, bậc 2024 thỏa mãn điều kiện P  2
x  2 chia hết cho P  x. Câu 3 (2,0 điểm). 2   2 x  x  x 1 2
 1 y  y  3
a) Giải hệ phương trình 
 x, y  . 2
y  2x  2  3  y   1  2 y  2x 
b) Bạn An viết lên trên bảng 11 số nguyên dương (không nhất thiết phân biệt) có tổng bằng
30. Chứng minh rằng bạn An có thể xóa đi một số số sao cho các số còn lại trên bảng có tổng bằng 10.
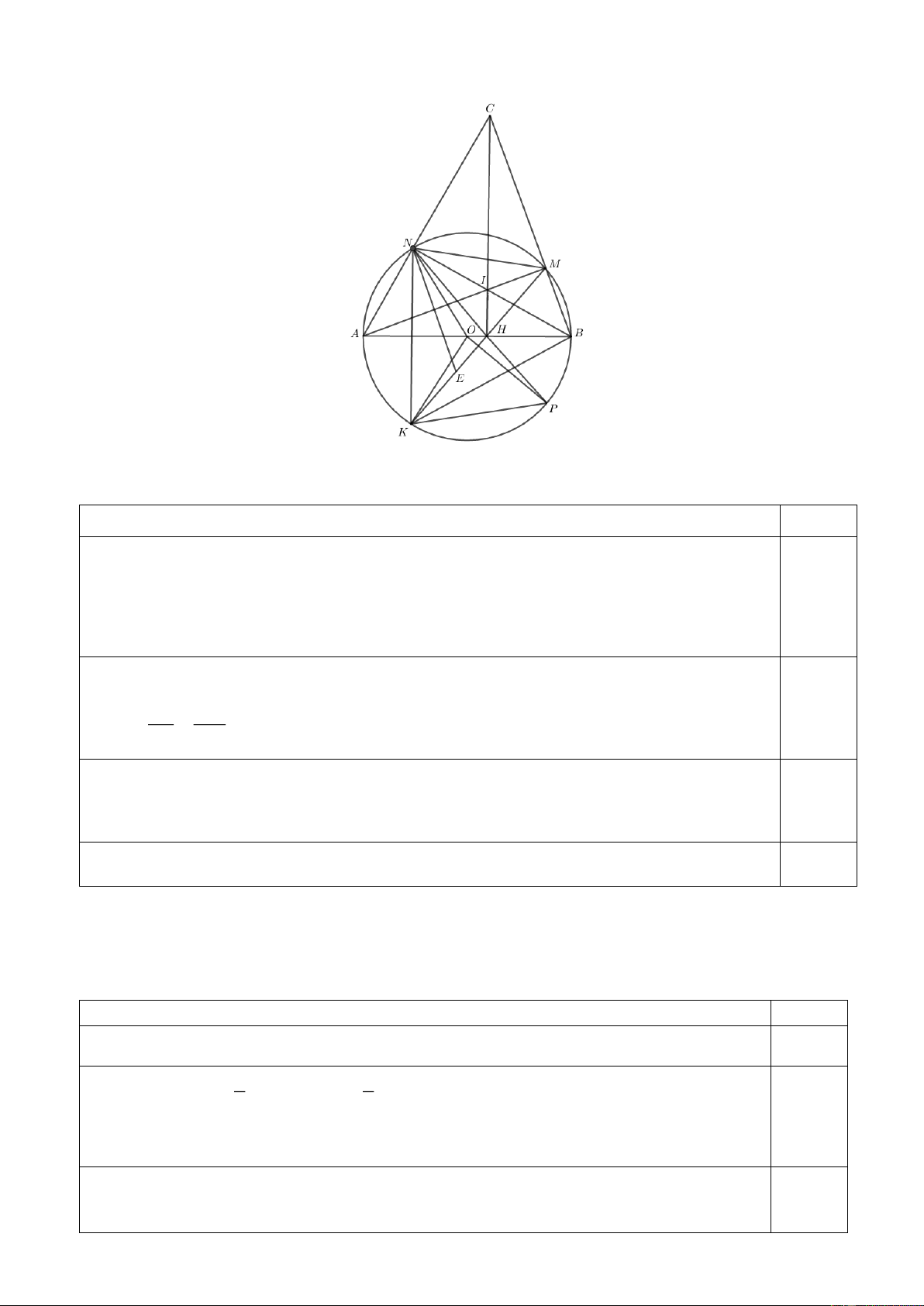
Câu 4 (3,0 điểm). Trên đường tròn tâm O đường kính AB  2R lấy điểm N sao cho AN  R và M
là một điểm thay đổi trên cung nhỏ BN ( M khác B và N ). Gọi I là giao điểm của AM và BN , H
là hình chiếu của I trên AB, IH cắt AN tại C, K là điểm đối xứng với N qua . AB
a) Chứng minh CM.CB  CI.CH và ba điểm K , H , M thẳng hàng.
b) Gọi P là giao điểm thứ hai của NH và O. Chứng minh tâm đường tròn ngoại tiếp tam
giác HPK thuộc đường thẳng cố định khi M thay đổi.
c) Xác định vị trí của điểm M để tổng MB  MN đạt giá trị lớn nhất.
Câu 5 (1,0 điểm). Xét các số thực dương a, b, ;
c tìm giá trị nhỏ nhất của biểu thức a b c F    . 2 2 2 a  9bc b  9ac c  9ab
.......................Hết.....................
Họ và tên thí sinh:………………………………………………Số báo danh:........................
Cán bộ coi thi không giải thích gì thêm. Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 PHÚ THỌ
TRUNG HỌC PHỔ THÔNG CHUYÊN HÙNG VƯƠNG NĂM HỌC 2023-2024
HƯỚNG DẪN CHẤM ĐỀ CHÍNH THỨC MÔN TOÁN
(Dành cho thí sinh thi chuyên Toán)
Hướng dẫn chấm có 06 trang
I. Một số chú ý khi chấm bài
- Đáp án chấm thi dưới đây dựa vào lời giải sơ lược của một cách. Khi chấm thi giám khảo cần
bám sát yêu cầu trình bày lời giải đầy đủ, chi tiết, hợp logic và có thể chia nhỏ đến 0,25 điểm.
- Thí sinh làm bài theo cách khác với hướng dẫn chấm mà đúng thì tổ chấm cần thống nhất cho
điểm tương ứng với thang điểm của hướng dẫn chấm.
- Điểm bài thi là tổng điểm các câu không làm tròn số.
II. Đáp án – thang điểm
Câu 1 (2 điểm).
a) Tìm tất cả các giá trị của tham số m để phương trình 2
x  m   2 2
1 x  m  2m  8  0 có hai
nghiệm phân biệt x , x thỏa mãn x  6  x . 1 2 1 2 Đáp án Điểm Xét phương trình: 2
x  m   2 2
1 x  m  2m  8  0. 2 Ta có :     m      2 ' 1
m  2m  8  9  0, m
 nên phương trình luôn có hai nghiệm 0,25
phân biệt x , x . 1 2
Ta tìm được hai nghiệm của phương trình là x  m  4 và x  m 2. 0,25
Trường hợp 1 : x  m  4, x  m  2, bài toán trở thành : 1 2 m  4  6 
m  2  m  2  m  2 m  2   0,25 m  2  0  m  2   m  1           m   m  2   1 2 2  m  2
m  3m  2  0  m  2  m  2 
Trường hợp 2: x  m  2, x  m  4, bài toán trở thành : 1 2 m  2  6 
m  4  m  8  m  4 m 8  0 m  8  m  8      0,25 m  4  0  m  4
 m  4 (vô nghiệm).      m  8  2 2  m  2
m 15m  62  0 m  
Vậy m  1, m  2 thỏa mãn là các giá trị phải tìm. 1 1
b) Cho f  x  1 
với x  0, x  1  . Tính f  
1  f 2  f 3  ...  f 2023. 2 x x  2 1 Đáp án Điểm 1 1 1 1
Ta có: f  x  1  1  với x  0. 2 0,25 x x  2 1 x x 1
Thật vậy, khi x  0, hai vế của đẳng thức đều dương nên bình phương hai vế của đẳng thức trên, ta được: 1 1 1 1 2 2 2 1  1     2 x x  2 2 1 x x  2 1 x x 1 x  x   1 0,25 1 1 1 1 2 2 1 1   1  1     2  (luôn đúng) 2   x x  2 2 1 x x  2 1 x x 1  x x 1 Áp dụng ta được: 0,25 Trang 2 f   1 1    f   1 1    f   1 1    f   1 1 1 1 ; 2 1 ; 3 1 ; ; 2023  1  ; 1 2 2 3 3 4 2023 2024 
Vậy f    f    f     f   2 1 2024 1 1 2 3 ... 2023  2024   . 0,25 2024 2024
Câu 2 (2,0 điểm).
a) Cho các số nguyên a, b, c, d thỏa mãn điều kiện 3 3 3 3
a  b  8c  28d  0.
Chứng minh rằng     2 a b c d chia hết cho 9. Đáp án Điểm Từ giả thiết 3 3 3 3
a  b  8c  28d  0 3 3 3 3 3 3
 a  b  c  d 9c  27d  0 3 3 3 3 3 3
 a  b  c  d  9c  27d . 0,25 Vì 3 3
9c  27d chia hết cho 3 nên 3 3 3 3
a  b  c  d chia hết cho 3. Mà  3 3 3 3
            3     3     3     3 a b c d a b c d a a b b c c d  d  0,25  a   1 aa   1  b   1 bb   1  c   1 cc   1  d   1 d d   1 chia hết cho 3.
Suy ra a  b  c  d chia hết cho 3. 0,25
Mà 3 là số nguyên tố, do đó     2 a b c d chia hết cho 9. 0,25
b) Chứng minh rằng tồn tại đa thức P  x có hệ số thực, bậc 2024 thỏa mãn điều kiện P  2
x  2 chia hết cho P  x. Đáp án Điểm
Xét đa thức P x   x  2024 1 . 0,5 2024 2024
Khi đó, ta có : P 2 x     2 x      2 2 2 1 x   1 . 0,25
Px    x  2024  x  2024 x  2024 2 2 2 1 1 1
chia hết cho P  x   x  2024 1 . 0,25
(Lưu ý: Học sinh có thể chọn các đa thức khác thỏa mãn vẫn cho điểm tối đa). Câu 3 (2,0 điểm). 2   2
x  x  x 1 2
1 y  y  3
a) Giải hệ phương trình: 
 x, y  . 2
y  2x   1  3  y   1  2
y  2x  2  Nội dung Điểm
Điều kiện:  y   2
1 y  2x  2  0. 2 2 Ta có  
1  2x 1 2x  
1  3   y   y  3. Đặt a  2x 1; b   y ta có 2 2
a  a  3  b  b  3  a  b   2 2
a  3  b  3   0 2 2 a  b  a  b   0,25 a  b 
 0  a  b 1     0 2 2 2 2
a  3  b  3 
a  3  b  3  2 2  a b a a 3 b b 3       
 a  b  0 do 1   0, a  ,b   2 2 2 2 
a  3  b  3
a  3  b  3  
 1 2x  y  2x 1 . y
Thay 1 2x  y, vào phương trình 2 , ta được:   2
 y  y    y   2 2 3 3
1 y  y  
1 . Điều kiện: y  1 0,25 Trang 3   2
y  y     y     y   2 1 2 1 3
1 y  y   1 2 y   1 y 1   3 1  0 2 2 y  y 1 y  y 1    t 1 Đặt y 1  t 
, t  0 , ta có phương trình: 2
2t  3t 1  0  1 (thỏa mãn) 2 y  y 1 t   2  1
y  0  x  y 1   2 Với 2 t  1 
 1  y  2 y  0   (thỏa mãn) 2 y  y 1 1 
y  2  x    2 0,25  5  37 3  37 y   x   1 y 1 1 2 4 Với 2 t  
  y  5y  3  0   (thỏa mãn) 2 2 y  y 1 2  5  37 3   37 y   x   2 4 0,25
Vậy hệ phương trình có nghiệm là:                x y 1 1 3 37 5 37 3 37 5 37 ;   ;0 ;  ;2 ;       ; ; ; .      2    2  4 2 4 2     
b) Bạn An viết lên trên bảng 11 số nguyên dương (không nhất thiết phân biệt) có tổng bằng
30. Chứng minh rằng bạn An có thể xóa đi một số số sao cho các số còn lại trên bảng có tổng bằng 10. Nội dung Điểm
Giả sử các số nguyên dương (không nhất thiết phân biệt) bạn An viết lên bảng là a , a ,
, a thỏa mãn a  a   a  30. 1 2 11 1 2 11
Gọi S  a , S  a  a , , S  a  a 
 a , S  a  a   a  a . 0,25 1 1 2 1 2 10 1 2 10 11 1 2 10 11
Ta có 1  S  30, i
 1,11 và S  S với mọi i  j;i, j  1,11. i i j
Chia các tổng S , S ,
, S cho 10, có ít nhất 2 số có cùng số dư. 1 2 11
Giả sử S , S S  S
có cùng số dư khi chia cho 10. Khi đó S  S 10 . 0,25 k m  k m  k m
Mà 1  S , S  30 nên S  S  10 hoặc S  S  20. k m k m k m
- Nếu S  S  10 thì các số a , a , , a k m m 1  m
còn lại trên bảng thỏa mãn điều kiện. 2 k 0,25
- Nếu S  S  20 thì a  a
  a  20 nên các số a ,a , ,a ,a ,a , ,a k m m 1  m2 k 1 2 m k 1  k  2 11 0,25
là các số còn lại trên bảng thỏa mãn điều kiện.
Câu 4 (3,0 điểm). Trên đường tròn tâm O đường kính AB  2R lấy điểm N sao cho AN  R và M
là một điểm thay đổi trên cung nhỏ BN ( M khác B và N ). Gọi I là giao điểm của AM và BN , H
là hình chiếu của I trên AB, IH cắt AN tại C, K là điểm đối xứng với N qua . AB
a) Chứng minh CM.CB  CI.CH và ba điểm K , H , M thẳng hàng.
b) Gọi P là giao điểm thứ hai của NH và O. Chứng minh tâm đường tròn ngoại tiếp tam
giác HPK thuộc đường thẳng cố định khi M thay đổi.
c) Xác định vị trí của điểm M để tổng MB  MN đạt giá trị lớn nhất. Trang 4 Vẽ hình:
a) Chứng minh rằng CM.CB  CI.CH và ba điểm K , H , M thẳng hàng. Đáp án Điểm
Tam giác ABC nhận I làm trực tâm do có hai đường cao BN ,CH cắt nhau tại I nên
BC  AI  
1 . Mặt khác AMB là góc nội tiếp chắn nửa đường tròn nên BM  AI 2. 0,25
Từ (1) và (2), suy ra ba điểm B, M ,C thẳng hàng.
Hai tam giác vuông BHC, IMC có C chung nên đồng dạng. CI CM 0,25 Suy ra 
 CM.CB  CI.CH. CB CH
Tứ giác ACMH nội tiếp nên BHM  ACM , BCNH nội tiếp nên AHN  ACM. 0,25
Suy ra AHN  BHM .
Mà do tính đối xứng nên AHN  AHK . Vậy AHK  BHM. Vậy K, H , M thẳng hàng. 0,25
(Lưu ý: Học sinh không giải thích rõ lý do để các góc bằng nhau vẫn cho điểm tối đa).
b) Gọi P là giao điểm thứ hai của NH và đường tròn O. Chứng minh tâm đường tròn
ngoại tiếp tam giác HPK thuộc đường thẳng cố định khi M thay đổi. Đáp án Điểm
Theo tính chất đối xứng, ta có: NOA  AOK 0,25 1 1
Mặt khác: AOK  NOK, NPK  NOK (cùng bằng một nửa góc NOK ). 2 2 0,25
Do đó AOK  NPK . Suy ra tứ giác OHPK nội tiếp.
Do đó tâm đường tròn ngoại tiếp tứ giác HPK chính là tâm đường tròn ngoại tiếp tam 0,25
giác OPK. Vậy tâm đường tròn ngoại tiếp tam giác HPK nằm trên đường trung trực của đoạn Trang 5 OK.
Do N cố định nên K cố định. Suy ra OK cố định, (Đpcm). 0,25
(Lưu ý: Học sinh không giải thích rõ lý do để các góc bằng nhau vẫn cho điểm tối đa).
c) Xác định vị trí của điểm M để tổng MB  MN đạt giá trị lớn nhất. Đáp án Điểm
Lấy E thuộc đoạn MK sao cho ME  MN, suy ra tam giác MNE cân tại M.
Mặt khác NME  NBK  2.NBA  2.30  60 (góc nội tiếp cùng chắn cung NK ) 0,25
Vậy tam giác MNE đều.
Xét tam giác MNB và ENK có: MN  NE, NB  NK.
Lại có: MNB  BNK  MNK, KNE  ENM  MNK , BNK  ENM  60 (do hai 0,25
tam giác MNE, BNK đều). Suy ra MNB  KN . E
Do đó tam giác MNB và ENK bằng nhau.
Suy ra MB  EK.  0,25
MB  MN  KE  ME  KM.
Vậy tổng MB  MN đạt giá trị lớn nhất khi KM là đường kính của đường tròn tâm . O 0,25
(Lưu ý: Học sinh không giải thích rõ lý do để các góc bằng nhau vẫn cho điểm tối đa).
Câu 5 (1,0 điểm). Xét các số thực dương a, b, ;
c tìm giá trị nhỏ nhất của biểu thức a b c F    . 2 2 2 a  9bc b  9ac c  9ab Đáp án Điểm a b c Ta có: F    . 2 2 2 a  9bc b  9ac c  9ab
Áp dụng bất đẳng thức Cauchy – Schwarz, ta có: 0,25 a b c
a b  c2    . 2 2 2 2 2 2 a  9bc b  9ac c  9ab
a a  9bc  b b  9ac  c c  9ab Mặt khác: 2 2 2 3 3 3
a a  9bc  b b  9ac  c c  9ab 
a a  9abc  b b  9abc  c c  9abc
 a  b  c 3 3 3
a  b  c  27abc. 0,25
a b  c2
a b  c3 Do đó : F           3 3 3 3 3 3
a  b  c  27 27 abc a b c a b c abc 3 Xét bất đẳng thức:
a b  c   3 3 3 10
9 a  b  c  27abc 3 3 3
 a  b  c  30a bb  cc  a  243abc luôn đúng theo bất đẳng thức AM - 0,25 GM.
Do đó a  b  c  abc 10 27 
a b c3 3 3 3 . 0,25 9 Trang 6
a b  c3 9 3 3 Suy ra:   F  , F 
 a  b  . c 3 3 3
a  b  c  27abc 10 10 10 3
Vậy giá trị nhỏ nhất của F là . 10
......................Hết..................... Trang 7