Đề thi tuyển sinh vào lớp 10 THPT Chuyên năm 2018-2019 chuyên toán đề chính thức Sở GD Quảng Nam (có đáp án và lời giải chi tiết)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUẢNG NAM NĂM HỌC 2018-2019 ĐỀ CHÍNH THỨC
Môn thi : TOÁN (chuyên)
Thời gian : 150 phút (không kể thời gian giao đề)
(Đề thi có 01 trang) Ngày thi :
Câu 1 (2,0 điểm).  a 1 ab  a
  2a b  2 ab 
a) Cho biểu thức A      1 :      . ab  1 1 ab 1    ab 
với a  0; b  0 và ab  1.
Rút gọn biểu thức A và tìm giá trị lớn nhất của A khi a + b = ab .
b) Tìm tất cả các cặp số nguyên (x ; )
y thỏa mãn đẳng thức 2 2 x y  2 x  2 6y  2x . y
Câu 2 (2,0 điểm). a) Giải phương trình 3 2 3 2 3 2 3 2
x  4x  3  2x  3x  2  3x  2x  2  4x  9x  3  27 3 8x   18  3  y
b) Giải hệ phương trình  2 4x 6x    1 2  y y
Câu 3 (1,0 điểm). Cho hai hàm số 2
y  2x và y  mx . Tìm m để hai đồ thị của hai hàm số đã cho cắt
nhau tại ba điểm phân biệt là ba đỉnh của tam giác đều.
Câu 4 (2,0 điểm).
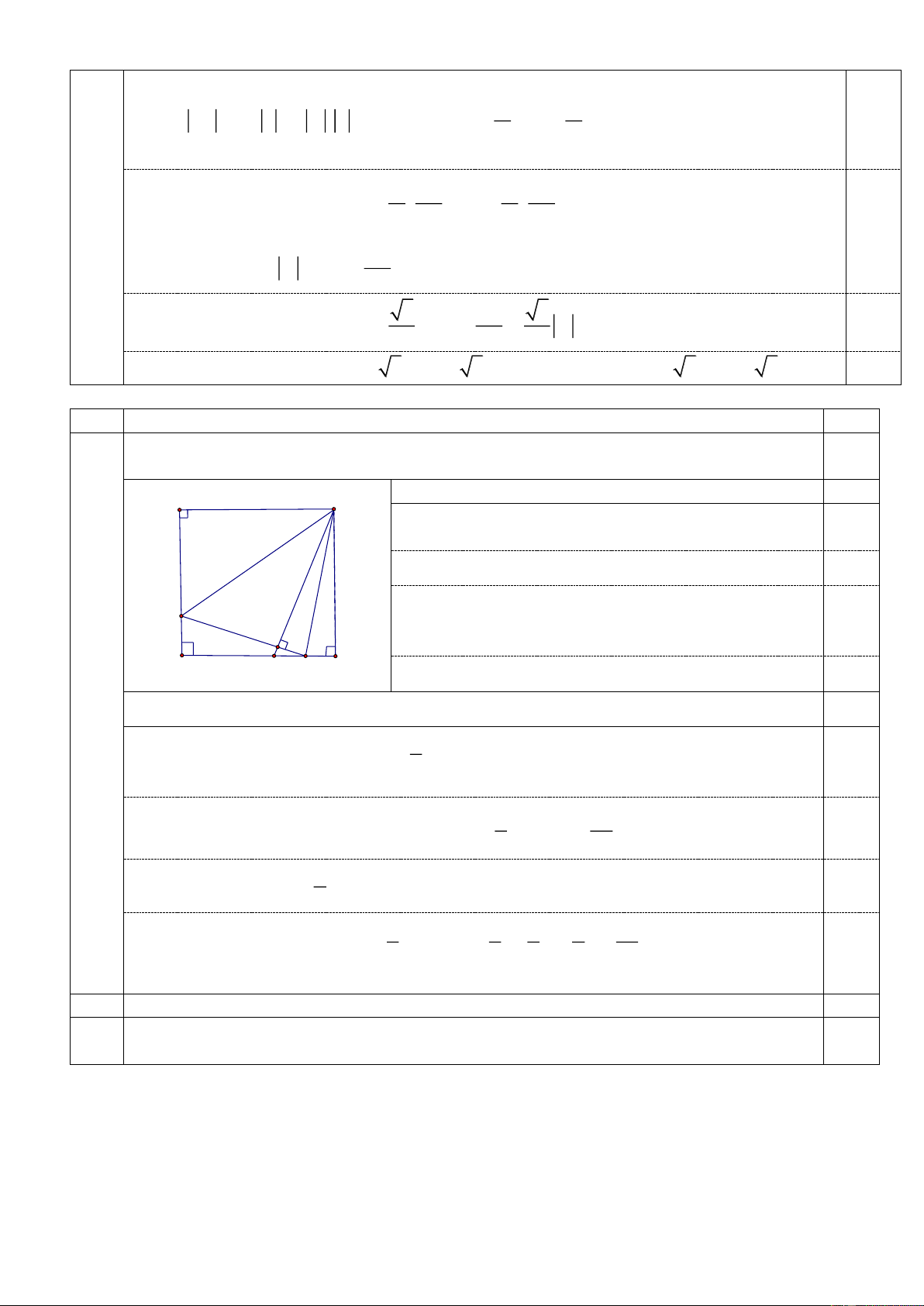
Cho hình vuông ABCD có cạnh bằng a . Trên cạnh AD lấy điểm M sao cho
AM  3MD. Kẻ tia Bx cắt cạnh CD tại I sao cho ABM  MBI . Kẻ tia phân giác của CBI ,
tia này cắt cạnh CD tại N.
a) So sánh MN với AM + NC.
b) Tính diện tích tam giác BMN theo a.
Câu 5 (2,0 điểm).
Cho đường tròn tâm O, dây cung AB không qua O. Điểm M nằm trên cung lớn AB.
Các đường cao AE, BF của tam giác ABM cắt nhau ở H.
a) Chứng minh OM vuông góc với EF.
b) Đường tròn tâm H bán kính HM cắt MA, MB lần lượt tại C và D. Chứng minh rằng
khi M di động trên cung lớn AB thì đường thẳng kẻ từ H vuông góc với CD luôn đi qua một điểm cố định.
Câu 6 (1,0 điểm). Cho ba số thực dương , a ,
b c . Chứng minh rằng 2 2 2 2 2 2 2 2 2 a  b b  c c  a
3(a  b  c )    a  b b  c c  a a  b  . c
--------------- HẾT ---------------
Họ và tên thí sinh: ........................................................................................ Số báo danh: ...................................... Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUẢNG NAM NĂM HỌC 2018-2019 HDC CHÍNH THỨC
HƯỚNG DẪN CHẤM MÔN TOÁN CHUYÊN
(Bản hướng dẫn này gồm 04 trang) Câu Nội dung Điểm Câu  a 1 ab  a
  2a b  2 ab  1
a) Cho biểu thức A      1 :      , ab  1 1 ab 1 ab (2,0)    
với a  0; b  0 và ab  1. 1,0
Rút gọn biểu thức A và tìm giá trị lớn nhất của A khi a + b = ab .
2  2 a 2a b  2 ab A  : 1 ab 1 0,25 ab 2(1  a ) 1   0,25 2 ab (1  a ) ab a + b 1 1 1 1
Khi a  0; b  0, a + b = ab   1    1   1 0,25 ab a b a b 2   Do đó 1 1 1 1 1 1 A  (1  )      
. Dấu “ = “ xảy ra  b  4; a  4 . Vậy giá b b 4  b 2  4 0,25 1
trị lớn nhất của A là
khi a  b  4 4
b) Tìm tất cả các cặp số nguyên (x ; )
y thỏa mãn đẳng thức 2 2 x y  2 x  2 6y  2x . y 1,0
- Với y  0 , ta có x  0 .
- Với y  0 , ta có: 2 2 2 2 2 2 2 (x  2 2 2   0,25
y  xy  x y  y  x  y  x   ) y x y x 6 2 5 ( ) 5  2 a a . 2 y
 x  a  5  x  3 2 2
x  a  5    x  3   0,25
 x  a  1  x  3   y  1  Khi 2
x = 3  3y  6 y  9  0   0,25  y  3  y 1 Khi 2 x = 3
-  3y  6 y  9  0    y  3  0,25 Vậy  ; x y  
 0;0;3; 1;3;3; 3  ;  1 ; 3  ; 3   Câu Nội dung Điểm
Câu a) Giải phương trình 3 2 3 2 3 2 3 2
x  4x  3  2x  3x  2  3x  2x  2  4x  9x  3 1,0 Trang 2 2 Đặt 3 2 3 2 3 2 3 2 a 
x  4x  3; b  2x  3x  2; c  3x  2x  2; d 
4x  9x  3 . (2,0)
a  b  c  d (1) 0,25 Ta có  3 3 3 3
a  b  c  d (2)
 a  b3  aba  b  c  d 3 (2) 3
 3cd c  d  0,25 
       a  b ab a b cd a
b  ab  cd  7  69 x  2
-Với a  b , ta có 3 2 3 2 2
x  4x  3 
2x  3x  2  x  7x  5  0    0,25 7  69 x   2
-Với ab  cd , ta có   3  11 3  11   2
x  4x  3 2
2x  3x  2   2
3x  2x  2 2
4x  9x  3  x  0  ;1; ;   0,25 2 2   3  11 3  11 7  69 7  69
Vậy pt có 6 nghiệm x  0; x  1; x  ; x  ; x  ; x  2 2 2 2  27 3 8x   18  3  y
b) Giải hệ phương trình  1,0 2 4x 6x    1 2  y y  27  3 3 8x   18     3 3 3  (2x)   y    18    y   . 2 4x 6x  0,25    3  3  1 2x. 2x   3 2     y y  y y 
a3  b3 18 a b  Đặt 3 3 a  2 ; x b = . Ta có   ...   y
ab(a b)  3 ab  1 0,25  3  5 3  5   3  5 3  5 
Giải tìm được  a  ;b 
 hoặc  a  ;b   0,25 2 2   2 2       3 5 6 3  Tìm đượ 5 6 c nghiệm  ;
x y của hệ là  ; ;  ;   0,25 4   3 5 4   3    5  Câu Nội dung Điểm
Câu Cho hai hàm số 2
y  2x và y  mx . Tìm m để hai đồ thị của hai hàm số đã cho cắt 3
nhau tại ba điểm phân biệt là ba đỉnh của tam giác đều. 1,0 (1,0) Trang 3
Phương trình hoành độ giao điểm 2 2 m m
2x  mx  2 x  m . x  0  x  0; x  ; x   0,25 2 2 2 2
 m m   m m 
Gọi ba giao điểm là O(0;0); A ; ; B  ;  
và H là giao điểm của AB và trục 2 2   2 2      0,25 2 m
tung, suy ra AB  m ; OH  2 2 3 m 3
Tam giác OAB đều  OH  AB   m 0,25 2 2 2
Giải và tìm được m  0; m  3; m   3 , loại m  0 . Vậy m  3; m   3 0,25 Câu Nội dung Điểm
Câu a) So sánh MN với AM + NC. 1,0 4 (2,0)
Hình vẽ phục vụ câu a) 0,25 A B
Trên cạnh BI lấy điểm H sao cho BH = BA = a.
 ΔABM  ΔHBM 0,25
và ΔHBN  ΔCBN Suy ra 0 0
BHM  BAM  90 ; BHN  BCN  90 0,25
Suy ra M; H; N thẳng hàng, do đó M
MN = MH + HN = AM + NC. 0,25 H D C I N
Ghi chú: không có hình không chấm.
b) Tính diện tích tam giác BMN theo a. 1,0 Đặ 3
t NC  x  MN  AM  NC 
a  x ; DN  a  x 4 0,25 2 2   Theo đị 2 2 2 3 a 2
nh lí Pitago MN  MD  DN  a  x     a  x 0,25  4  16 a
Giải và tìm được x  0,25 7 1 1  3 a  25
Diện tích tam giác BMN bằng 2 BH.MN  a a   a   . 2 2  4 7  56 0,25 Câu Nội dung Điểm
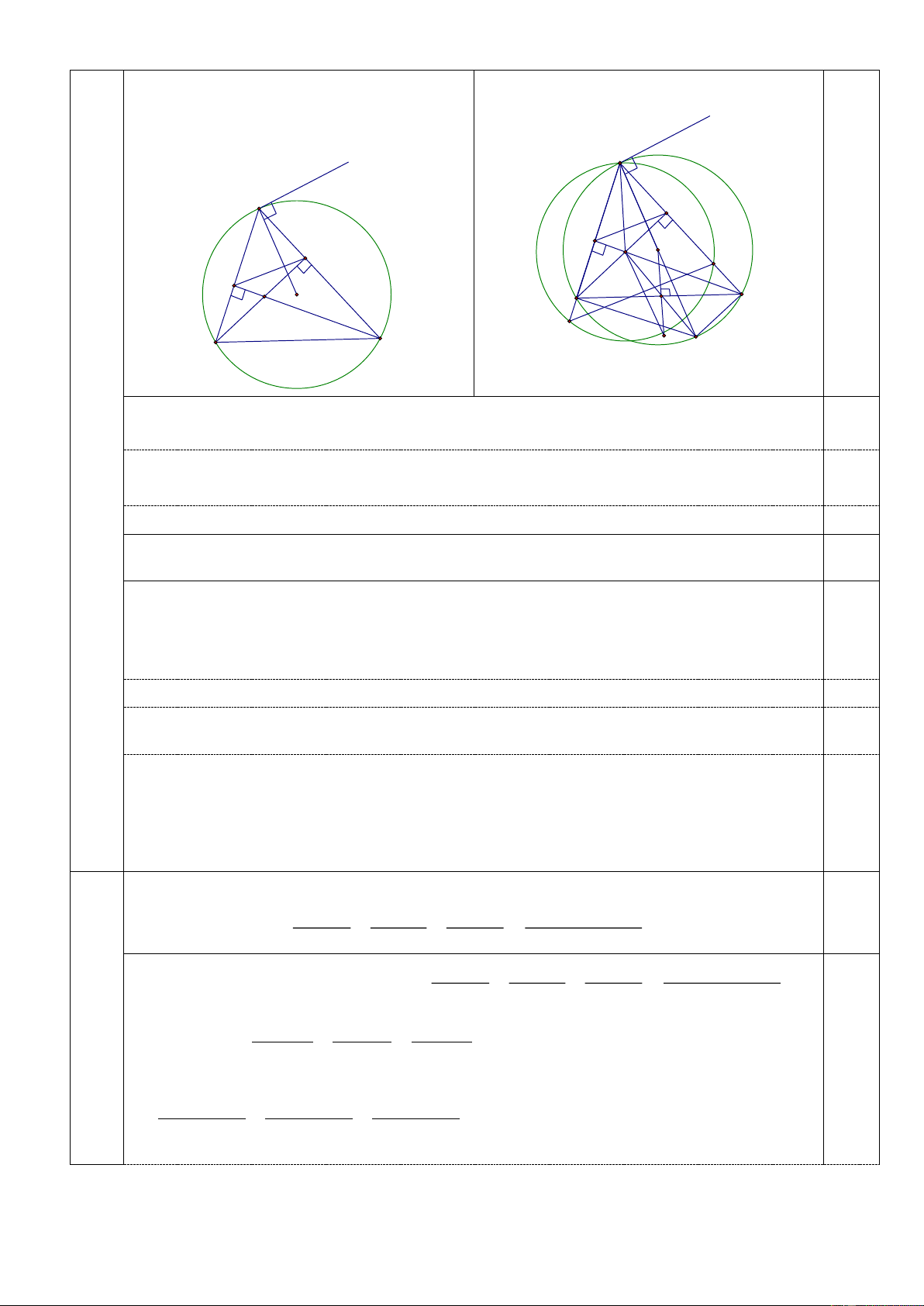
Câu a) Chứng minh OM vuông góc với EF. 1,0 5 Trang 4
(2,0) Hình vẽ phục vụ câu a (không tính điểm
hình vẽ câu b, không có hình không x chấm) M x M E F 0,25 E D O H F A O B H I C B K A N Tứ giác ABEF có 0
AEB  AFB  90 nên nội tiếp đường tròn  MEF  FAB 0,25
Từ M kẻ tia tiếp tuyến Mx với đường tròn tâm O (như hình vẽ), ta có 0,25
xMB  MAB  FAB . Suy ra xMB  MEF  Mx / /EF
Theo tính chất của tiếp tuyến đường tròn, ta có MO  Mx  MO  EF 0,25
b) Chứng minh rằng khi M di động trên cung lớn AB thì đường thẳng kẻ từ H vuông 1,0
góc với CD luôn đi qua một điểm cố định.
Kẻ đường kính MN của đường tròn tâm O. Tứ giác AHBN có AH song song với NB
(cùng vuông góc với MB), có BH song song với NA (cùng vuông góc với MA) nên là 0,25
hình bình hành. Suy ra HN cắt AB tại trung điểm I của mỗi đoạn. Do đó
MH / /OI; MH  2.OI
Gọi K là điểm đối xứng của O qua I, suy ra OK = 2OI và điểm K cố định 0,25
Tứ giác MHKO có MH, OK song song và bằng nhau ( cùng gấp đôi OI) nên là hình 0,25
bình hành. Suy ra HK / /MO
Xét đường tròn tâm H bán kính HM, theo tính chất đường kính vuông góc với dây
cung, suy ra E là trung điểm của MD và F là trung điểm của MC. Do đó
EF / /CD  MO  CD  HK  CD . 0,25
Vậy khi M đi động trên cung lớn AB thì đường thẳng kẻ từ H vuông góc với CD
luôn đi qua điểm cố định K.
Câu Cho ba số thực dương , a ,
b c . Chứng minh rằng; 6 2 2 2 2 2 2 2 2 2 a  b b  c c  a
3(a  b  c ) 1,0 (1,0)    a  b b  c c  a a  b  c 2 2 2 2 2 2 2 2 2 a  b b  c c  a
3(a  b  c )
Với ba số thực dương , a , b c ta có    a  b b  c c  a a  b  . (1) c 2 2 2 2 2 2       
a  b  c a b b c c a 2 2 2   
  3(a  b  c )  a b b c c a       0,25 c  2 2
a  b  a 2 2
b  c  b 2 2 c  a  2 2 2   
 a  b  c a  b b  c c  a Trang 5 c  2 2 a  b  a  2 2 b  c  b  2 2 c  a 2 2 2   c   a   b   0 a  b b  c c  a 0,25
ac c  a
bc c  b
ab b  a
bc b  c
ab a  b
ac a  c        0 a  b a  b c  a c  a b  c b  c
ac c  a2
bc c  b2
ab b  a2      0,25
a  bb  c
a  ba  c a  cb  c 0. (2)
Với ba số thực dương , a ,
b c ta có (2) luôn đúng. Vậy (1) luôn đúng. (đpcm) 0,25 * Lưu ý:
Nếu thí sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì giám khảo vẫn
cho đủ số điểm từng phần như hướng dẫn quy định. Trang 6