

Preview text:
SỞ GD&ĐT HÒA BÌNH KỲ THI TUYỂN SINH VÀO LỚP 10 TRUNG HỌC PHỔ THÔNG
NĂM HỌC 2023 – 2024 ĐỀ THI MÔN TOÁN ĐỀ CHÍNH THỨC
(Dành cho thí sinh dự thi vào lớp chuyên Nga – Pháp – Trung) THUC Ngày thi: 08/6/2023
Thời gian làm bài: 150 phút, không kể thời gian giao đề.
Đề thi có 01 trang, gồm 04 câu.
Câu I (3,0 điểm)
1. Tính giá trị biểu thức: 2 A (1 5) 20 1 y 3 x
2. Giải hệ phương trình: 3 y 1 x 3. Giải phương trình: 4 2
x 3x 4 0
Câu II (3,0 điểm)
1. Trong mặt phẳng tọa độ Oxy cho đường thẳng (d) : y ax b . Tìm a, b biết
đường đường thẳng (d) đi qua (
A 1;2) và song song với đường thẳng (d ') : y 3x 2 . 2. Cho phương trình 2 2
x 2mx m m 1 0 (m là tham số).
a) Tìm giá trị của m để phương trình có hai nghiệm x , x . 1 2
b) Tìm hệ thức liên hệ giữa x và x không phụ thuộc vào tham số . m 1 2
3. Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Dì Út dự kiến trồng 160 cây Thanh Long trong một khu vườn hình chữ nhật theo
hàng, mỗi hàng có số cây bằng nhau. Do mở rộng diện tích khu vườn nên Dì Út đã trồng
thêm được 82 cây bằng cách trồng thêm 3 hàng, mỗi hàng thêm 2 cây so với dự định. Tính
số hàng cây và số cây Thanh Long ở mỗi hàng mà Dì Út dự định trồng trong vườn lúc đầu.
Câu III (3,0 điểm)
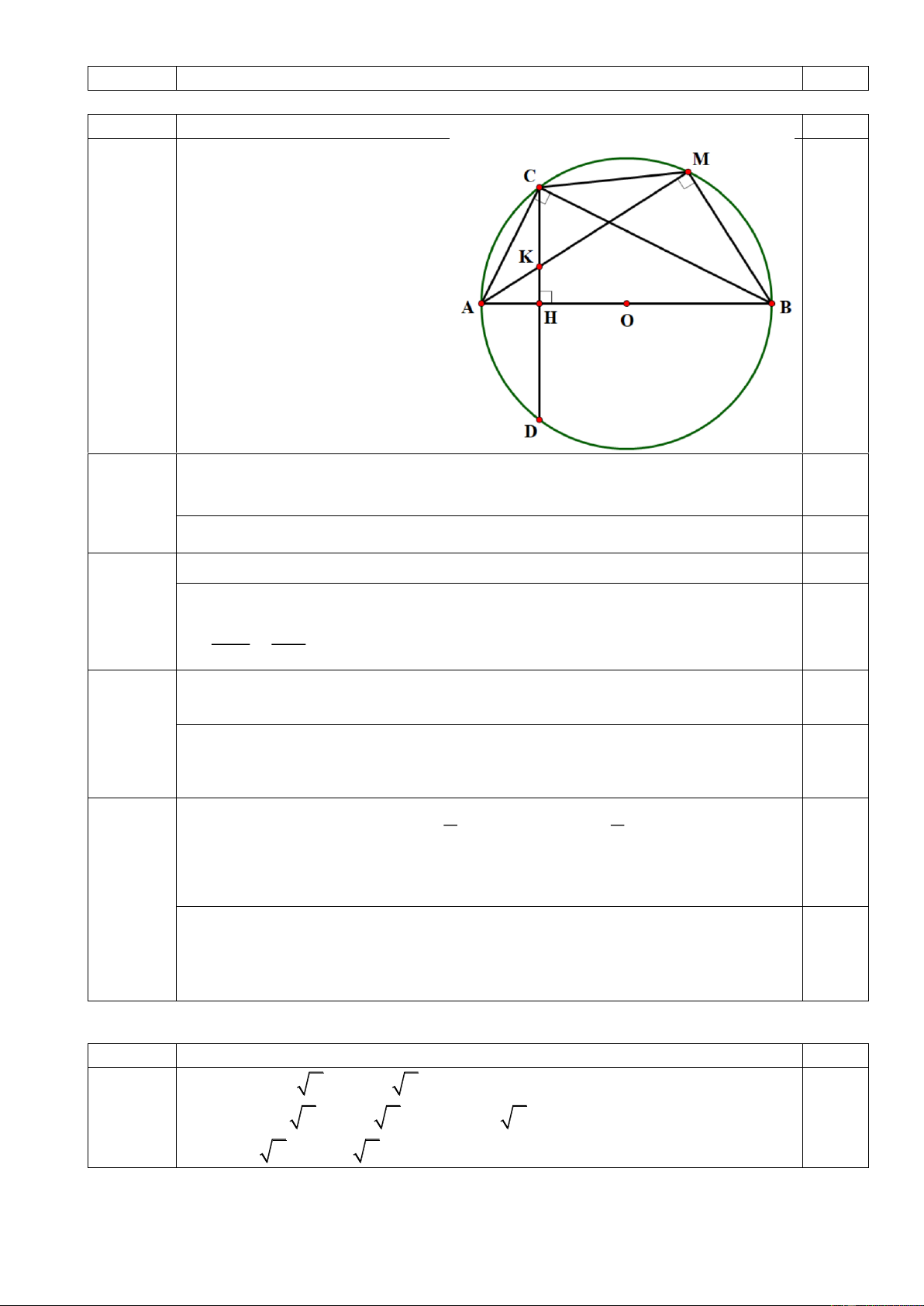
Cho đường tròn tâm O đường kính AB cố định. Vẽ dây cung CD vuông góc với
AB tại H sao cho AH .
AO Gọi K là điểm bất kỳ nằm trên đoạn CH , M là giao điểm
của tia AK với đường tròn (O). Chứng minh rằng:
a) Tứ giác BMKH nội tiếp được trong một đường tròn. b) 2
AC AM .AK. c) 2
AK.AM AH .HB AH .
d) Khi K di chuyển trên đoạn CH thì tâm đường tròn ngoại tiếp tam giác CMK
luôn thuộc một đường thẳng cố định.
Câu IV (1,0 điểm) 1. Tìm cặp số ( ; x y) thỏa mãn: 2
4x 2y 4x y 4x 6 y 5 0 .
2. Cho a; b là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức: a + b P .
a 8a + b b 8b + a
-------- HẾT --------
Họ và tên thí sinh: ............................................ Số báo danh: .................... Phòng thi: ......
Giám thị 1: ............................................ Giám thị 2: ......................................................... Trang 1
SỞ GD&ĐT HÒA BÌNH KỲ THI TUYỂN SINH VÀO LỚP 10 TRUNG HỌC PHỔ THÔNG
NĂM HỌC 2023 – 2024
HƯỚNG DẪN CHẤM MÔN TOÁN ĐỀ CHÍNH THỨC
(Dành cho thí sinh dự thi vào lớp chuyên Nga – Pháp – Trung) THUC Ngày thi: 08/6/2023
Hướng dẫn chấm có 03 trang
Câu I (3,0 điểm) Phần, ý Nội dung Điểm 1 2
A (1 5) 20 1 2 5 5 2 5 6 1,0 ĐKXĐ: x 0 0,25 1 4 y 3 4 x x x 1 (TM ) 2 3 3 y 2 0,5 y 1 y 1 x x Kết luận:... 0,25 4 2
x 3x 4 0 Đặt 0,25 2
x t (t 0) ta được phương trình: 2
t 3t 4 0 3
Tìm được t 1 (KTM ); t 4 (TM ) 0,5
Suy ra được nghiệm của phương trình: x 2; x 2. 0,25
Câu II (3,0 điểm) Phần, ý Nội dung Điểm
(d) song song với đường thẳng (d') a 3;b 2 0,5 1
(d) : y 3x b (b 2)
(d) đi qua A(–1;2) 2 3.(1) b b 5 (TM ) 0,5 2a
Phương trình có nghiệm ' 0 m1 0 m 1 0,5
x x 2m (1)
Áp dụng hệ thức Vi – ét: 1 2 2
x x m m 1 (2) 1 2 Từ (1) ta có: x x 1 2 m , thay vào (2) ta được: 0,5 2b 2 2 x x x x 1 2 1 2 x x 1 ... 1 2 2 2 KL: ...
Gọi số hàng cây Thanh Long Dì Út dự định trồng lúc đầu là x ( x N*) 160 0,25
Số cây trồng ở mỗi hàng ban đầu là: (cây) x
Lập được phương trình: 160 242 2 3 x x 0,25 3
Giải phương trình tìm được: x 8 (TM ); x 30 (TM ).
Nếu số hàng cây là 8 thì số cây ở mỗi hàng là 20; 0,5
Nếu số hàng cây là 30 thì số cây ở mỗi hàng là 16 160 : 30 (loại). 3 Trang 2 Vậy: ...
Câu III (3,0 điểm) Phần, ý Nội dung Điểm Ta có 0
AMB 90 (góc nội tiếp chắn nửa đường tròn) 0,5 a 0 BHK 90 (gt) Suy ra 0
AMB BHK 180 tứ giác HKMB là tứ giác nội tiếp 0,5
AB CD AC AD ACK AMC 0,5
ACK ” AMC (vì A chung; ACK AMC ) b AC AK 0,5 2
AC AK.AM (1) AM AC 0
ACB 90 (góc nội tiếp chắn nửa đường tròn) 0,25
Suy ra tam giác ABC vuông tại C 2 CH H . A HB (2) b
Áp dụng định lí Pytago trong tam giác HCA vuông tại H, ta có: 0,25 2 2 2
CH AH AC (3)
Từ (1), (2), (3) AH2 + AH.HB = AK.AM đpcm. 1 1
Có ACK CMK , mà CMK
sđCK ACK sđCK . 2 2 0,25
nên CA là tiếp tuyến của đường tròn ngoại tiếp MCD (Định lí đảo góc tạo b
bởi tia tiếp tuyến và dây cung).
Mà CA CB tâm đường tròn ngoại tiếp MCK nằm trên CB.
Ta có A, B, H cố định nên dây CD cố định. Suy ra CB cố định. 0,25
Vậy tâm đường tròn ngoại tiếp tam giác CMK luôn thuộc đường thẳng CB cố định.
Câu IV (1,0 điểm) Phần, ý Nội dung Điểm 2
4x 2 y 4x y 4x 6 y 5 0 ( y 0) 2 2
4x 4x( y 1) ( y 1) y 4 y 4 0 0,25 1 2 2
(2x y 1) ( y 2) 0 Trang 3 y 4 (TM ) y 2 0 1 . Vậy 1 ( ; x y) ( ; 4) 0,25
2x y 1 0 x 2 2 a + b 3(a + b) Ta có:
a 8a + b b 8b + a
9a 8a + b 9b 8b + a (1)
Áp dụng bất đẳng thức Cô-si cho các số dương ta được: 0,25
9a + (8a + b) 17a + b 9a 8a + b 2 2 2 9b + (8b + a) 17b + a
9b 8b + a 3 2 2 2
Từ (2) và (3) suy ra: 9a8a + b 9b8b + a 9a + 9b 4 Từ (1) và (4) suy ra: a + b 3(a + b) 1 .
9a 8a + b 9b 8b + a 9a + 9b 3 0,25
Dấu bằng xảy ra khi và chỉ khi a = b. Vậy 1 MinP , đạt khi a = b. 3
* Chú ý: Các lời giải đúng khác đều được xem xét cho điểm tương ứng.
-------- HẾT -------- Trang 4




