SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT TỈNH HÀ GIANG NĂM HỌC 2023 - 2024
ĐỀ THI MÔN: TOÁN HỌC ĐỀ CHÍNH THỨC
(dành cho thí sinh thi chuyên Toán, chuyên Tin)
Thời gian làm bài: 150 phút Ngày thi: 09/06/2023 Câu 1 (2,0 điểm):
a) Tính giá trị biểu thức A 
2024  2 2023  2024  2 2023 . 1 2 2 x  3 1 b) Rút gọn B   
(với x  0 ). Tìm x để B  . x x  3 x  3 x 7 Câu 2 (2,5 điểm):
a) Xác định hệ số a,b để đường thẳng d  : y  ax  b đi qua hai điểm A2;4 và B  1  ; 5  .
b) Tìm m để phương trình 2
x  x ( m 1)  0 có hai nghiệm phân biệt x ; x thỏa 1 2  1 1  mãn 4 
  x x  3  0. 1 2 x x  1 2 
Câu 3 (1,0 điểm): Tìm nghiệm nguyên của phương trình x  2yx  y  5x  4y  1  .
Câu 4 (3,5 điểm): Cho tam giác đều ABC,cạnh a, đường cao AH. M là một điểm thay
đổi trên cạnh BC, qua M kẻ MP vuông góc với AB, MQ vuông góc với AC. Gọi O là
trung điểm của AM.
a) Chứng minh năm điểm A,P,M ,H ,Q cùng thuộc một đường tròn.
b) Tứ giác OPHQ là hình gì? Vì sao?
c) Xác định vị trí của điểm M trên cạnh BC để độ dài PQ nhỏ nhất, tìm độ dài đó theo a.
Câu 5 (1,0 điểm): Cho hai số thực a,b thay đổi thỏa mãn điều kiện a  b  4. Tìm giá trị
nhỏ nhất của biểu thức P  6 2 16 2 2 a  b    3. a  b
----------- HẾT ----------
(Thí sinh không được sử dụng tài liệu; Cán bộ coi thi không giải thích gì thêm).
Họ và tên thí sinh: ………….……………..Số báo danh: .…………………………….
Họ tên CBCT 1: ……………………..........Họ tên CBCT 2: …….………………….... Trang 0
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT TỈNH HÀ GIANG NĂM HỌC 2023 - 2024
HDC ĐỀ CHÍNH THỨC
Hướng dẫn chấm thi môn Toán
dành cho thí sinh thi chuyên Toán, chuyên Tin
(Bản hướng dẫn chấm gồm 04 trang)
Một số lưu ý khi chấm
1. Nếu thí sinh không làm bài theo cách nêu trong đáp án mà vẫn đúng và biện luận
chặt chẽ (cho dù dùng kiến thức nâng cao hoặc vượt chương trình) thì vẫn cho đủ điểm như
hướng dẫn quy định (đối với từng phần)
2. Việc chi tiết hóa thang điểm (nếu có) so với thang điểm hướng dẫn chấm phải bảo
đảm không sai lệch với hướng dẫn chấm và được thống nhất thực hiện trong hội đồng chấm thi.
3. Điểm bài thi là tổng điểm các câu thành phần và không được làm tròn; đề thi thang điểm 10. Câu 1 (2,0 điểm):
a) Tính giá trị biểu thức A  2024  2 2023  2024  2 2023 . 1 2 2 x  3 1 b) Rút gọn B   
(với x  0 ). Tìm x để B  . x x  3 x  3 x 7 Câu Đáp án Điểm A 
2024  2 2023  2024  2 2023 0,25 Câu 1a
 2023 2 2023 1  2023 2 2023 1 (0,5 đ) 2 2   2023   1   2023   1
 2023 1 2023 1  2  0,25 Với x  0 , ta có 1 2 2 x  3
x  3  2 x  2 x  3 B     0,5 x x  3 x  3 x x  x  3 Câu 1b x 1   (1,5 đ) . 0,5 x  x  3 x  3 1 1 1 B     x  3  7 0,25 7 x  3 7
 x  4  x 16 . 0,25 Câu 2 (2,5 điểm):
a) Xác định hệ số a,b để đường thẳng d  : y  ax b đi qua hai điểm A2;4 và B  1  ; 5  . Trang 1
b) Tìm m để phương trình 2
x  x  ( m 1)  0 có hai nghiệm phân biệt x ; x thỏa 1 2  1 1  mãn 4 
  x x  3  0. 1 2 x x  1 2  Câu Đáp án Điểm
d : y  ax b đi qua hai điểm A2;4 và B 1  ; 5   nên ta có hệ
2a  b  4 phương trình 0,5  Câu 2a
a  b  5 (1,0 đ) a  3   b   2  0,5
Vậy a  3;b  2  .
Để phương trình có hai nghiệm phân biệt thì   4m3  0 0,5 3 Suy ra m  . 0,25 4 x  x  1 Theo hệ thức Vi-et ta có 1 2  0,25 x x  (  m 1)  Câu 2b 1 2
(1,5 đ) Theo đề bài:  1 1   x  x  4 1 2 0,25 4 
  x x  3  0  4
  x x  3  0   m  2  0 1 2 1 2 x x  x .x m 1 1 2   1 2  Suy ra 2
m  m  6  0  m  3
 (loại) hoặc m  2 (thỏa mãn). 0,25
Vậy m  2 là giá trị cần tìm.
Câu 3 (1,0 điểm): Tìm nghiệm nguyên của phương trình x  2yx  y  5x  4y  1  . Câu Đáp án Điểm Ta có
x  2yx  y5x  4y  1  0,25
 x  2yx  y  3x  2y  2x  y  1 
 x  y  3x  2y  2  5 Vì x, y  ¢ nên: 0,25
x  y 3;x  2y  2  5; 
1 ,1;5 , 5  ;  1 , 1  ; 5   .       Câu 3 x y 3 5 x 1 TH1:    (Thỏa mãn) (1,0 đ)
x  2y  2  1 y  1  1  x  0,25
x  y  3  1  3 TH2:    (Không thỏa mãn)
x  2y  2  5 5 y   3  19  x 
x  y  3  5  3 TH3:    (Không thỏa mãn) 0,25
x  2y  2  1  5 y   3 Trang 2
x  y  3  1  x  5  TH4:    (Thỏa mãn)
x  2y  2  5  y  1 
Vậy  x; y  
 1; 1, 5  ;  1  .
Câu 4 (3,5 điểm): Cho tam giác đều ABC, cạnh a, đường cao AH. M là một điểm thay
đổi trên cạnh BC, qua M kẻ MP vuông góc với AB, MQ vuông góc với AC. Gọi O là
trung điểm của AM.
a) Chứng minh năm điểm A,P,M ,H ,Q cùng thuộc một đường tròn.
b) Tứ giác OPHQ là hình gì? Vì sao?
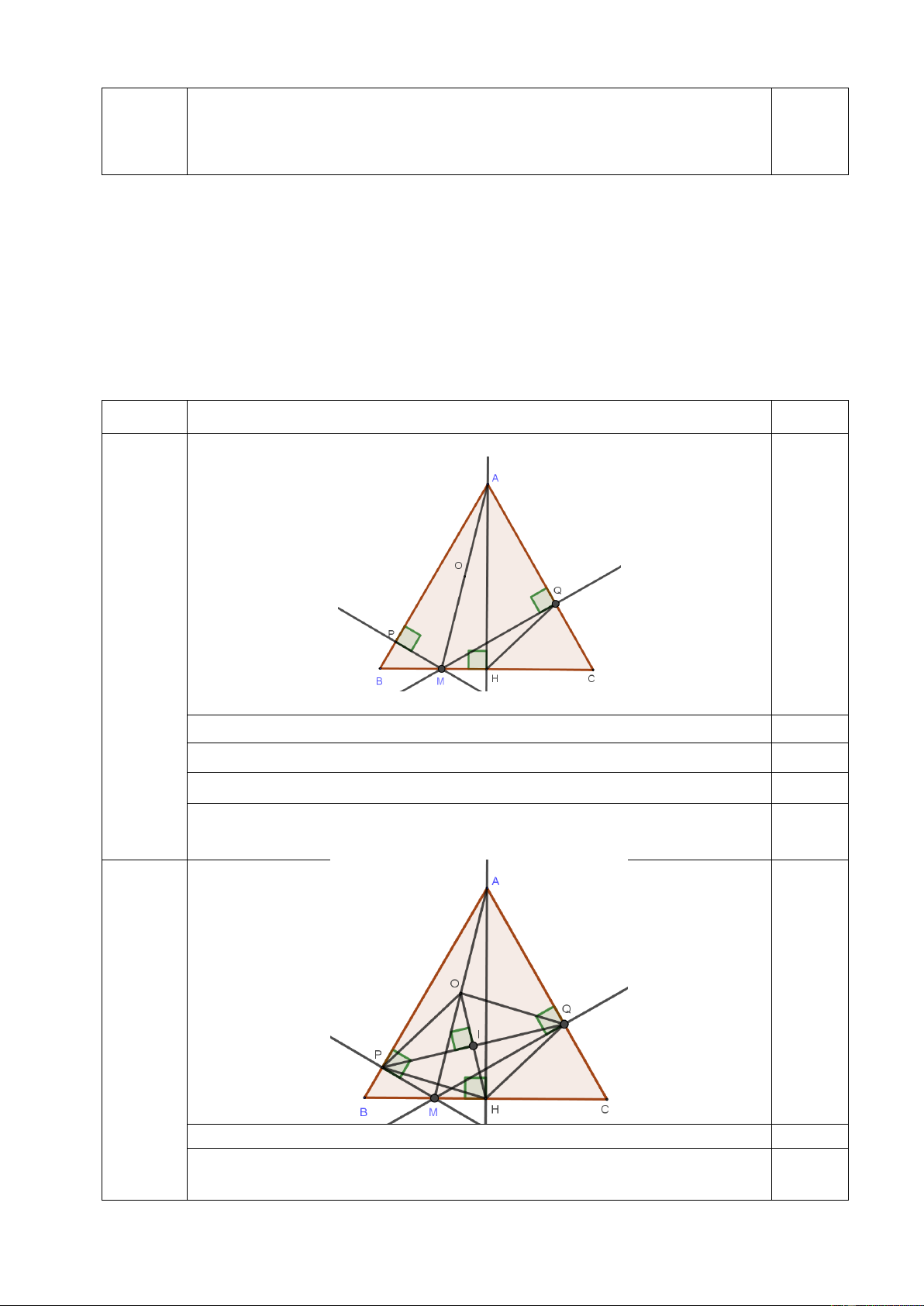
c) Xác định vị trí của điểm M trên cạnh BC để độ dài PQ nhỏ nhất, tìm độ dài đó theo a. Câu Đáp án Điểm Vẽ đúng hình đến ý a 0,25 Câu 4a (1,5 đ) Ta có · 0 APM  90 0,25 · 0 AHM  90 0,25 · 0 AQM  90 0,25 · · · Suy ra 0
APM  AHM  AQM  90 . Vậy năm điểm A,P,M ,H ,Q 0,5
cùng thuộc một đường tròn tâm O đường kính AM. Câu 4b (1,0 đ)
Theo chứng minh ý a, O
 PH cân tại O. 0,25 Lại có · · · 0
POH  2BAH  BAC  60 0,25 Suy ra O
 PH đều nên OP  PH  HO. Trang 3
Tương tự OQ  QH  HO. 0,25
Suy ra OP  OQ  QH  HP. Vậy tứ giác OPHQ là hình thoi. 0,25 Theo chứng minh ý b) · 0 POH  60 . 0,25
Gọi I là giao điểm của PQ và OH . Suy ra OI  PQ và PQ  2PI . 0,25 · 1 0 Câu 4c Trong I
 OP ta có PI  PO.sin IOP  AM .sin60 (1,0 đ) 2 0,25 0
 PQ  AM .sin60 .
PQ nhỏ nhất khi AM nhỏ nhất, khi đó M trùng H. 3 a 3 3 3a 0,25 Vậy 0
PQ  AH .sin 60  AH .  .  . 2 2 2 4
Câu 5 (1,0 điểm): Cho hai số thực a,b thay đổi thỏa mãn điều kiện a  b  4. Tìm giá trị 16
nhỏ nhất của biểu thức P  6 2 2 2 a  b    3. a  b Câu Đáp án Điểm
Với hai số thực a,b ta luôn có
a b2 a b2  a b2  a b   a b2 2 2 2 .
Đẳng thức xảy ra khi a b. 0,25 Từ đây ta được  2 2
2 a  b   a  b (do a  b  4 ). Khi đó P  6 2 16 16 2 2 a  b  
 3  6a  b   3 a  b a  b 0,25 16 Câu 5
 a  b 
 5a  b  3. (1,0 đ)  a b
Áp dụng bất đẳng thức cô-si cho hai số dương a  16 b và a  b ta được 0,25
P  a  b 16 
 a  b   a b 16 5 3 2 .
 5a  b  3  25. a  b a  b
Vậy giá trị nhỏ nhất của P là 25 đạt được khi a  b  4 
 a  b  2. 0,25 a  b
----------- HẾT ---------- Trang 4