Đề thi tuyển sinh vào lớp 10 THPT năm 2023-2024 môn toán Sở GD TP. Cần Thơ (có đáp án và lời giải chi tiết)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT
THÀNH PHỐ CẦN THƠ NĂM HỌC 2023-2024
Khóa ngày 05 tháng 6 năm 2023 ĐỀ CHÍNH THỨC MÔN: TOÁN (CHUYÊN)
(Đề thi có 02 trang)
Thời gian làm bài: 150 phút, không kể thời gian phát đề    Câu 1 (1,5 điể 2 x 9 x 3 2 x 1
m). Cho biểu thức P   
với x  0 và x  4, x  9. x  5 x  6 x  2 3  x
a) Rút gọn biểu thức P .
b) Tìm tất cả các số nguyên x sao cho P nhận giá trị là số chẵn.
Câu 2 (1,0 điểm). Trong mặt phẳng Oxy, cho đường thẳng d : y  2mx  4m  5,(m là tham số) và parabol 2
(P ) : y  x . Tìm tất cả giá trị của m để d cắt (P ) tại hai điểm phân biệt A, B sao cho ba
điểm O, A, B tạo thành tam giác vuông tại O.
Câu 3 (2,0 điểm). Giải phương trình và hệ phương trình sau: a) 2 (x  3) x
  8x  48  x  24. 3 3 x
  y  35  0 b)  . 2 2
2x  3y  4x  9y  0  Câu 4 (2,0 điểm).
a) Tìm tất cả số nguyên x, y thỏa mãn 2 2
x  2y  xy  2x  5y  5  0.
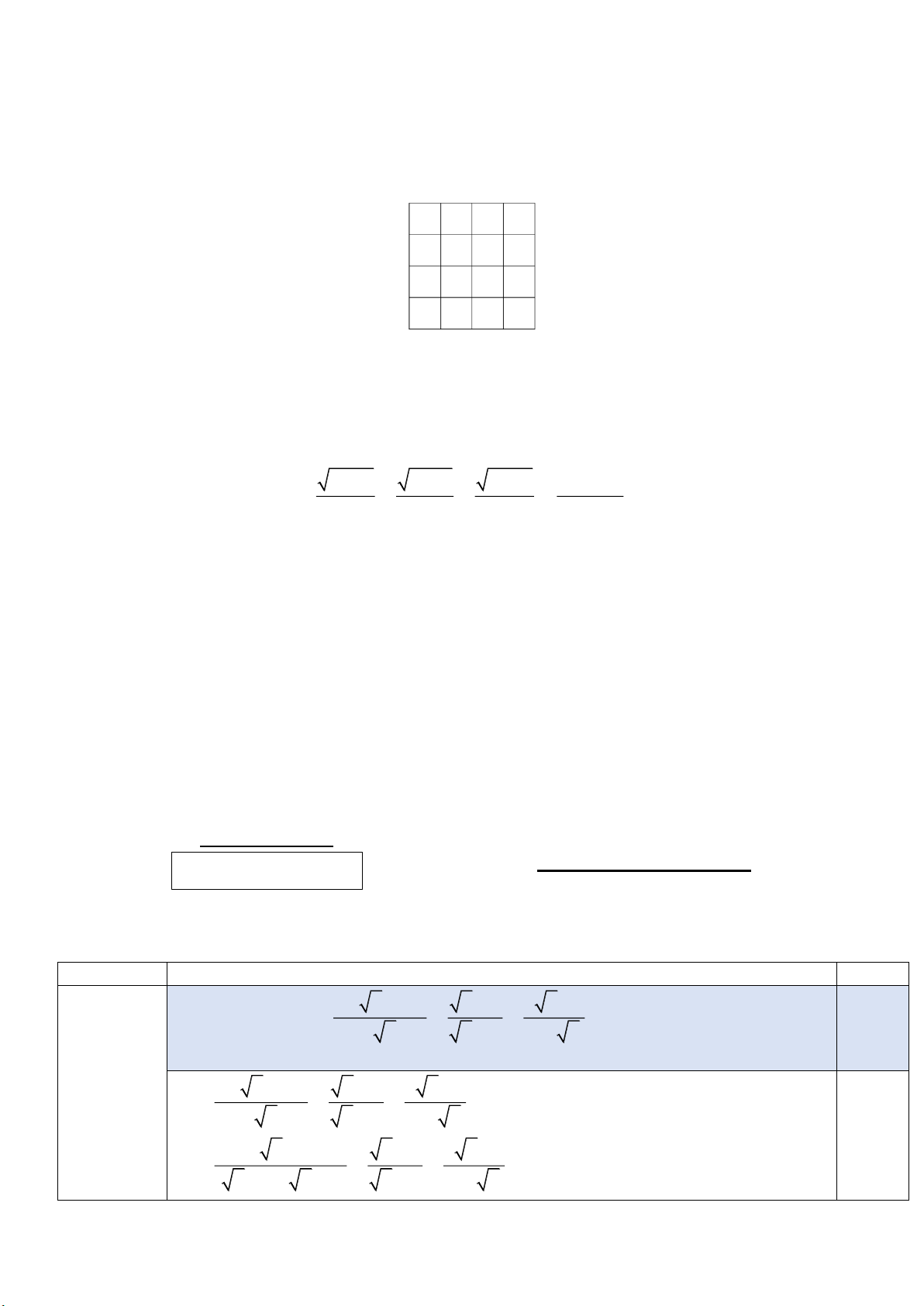
b) Một cái bình hình nón được đặt trên một mặt phẳng nằm ngang sao cho đỉnh của nó hướng
lên trên. Người ta rót nước vào bình cho đến khi mực nước dâng cao cách đỉnh 8 cm (như hình 1 ).
Sau đó, người ta đảo ngược cái bình lại sao cho đỉnh bình hướng xuống (như hình 2 ). Khi đó, người
ta đo được phần không gian trống của bình có chiều cao 2 cm. Biết rằng lượng nước bên trong bình
không thay đổi. Tính chiều cao của cái bình đã cho. Hình 1 Hình 2
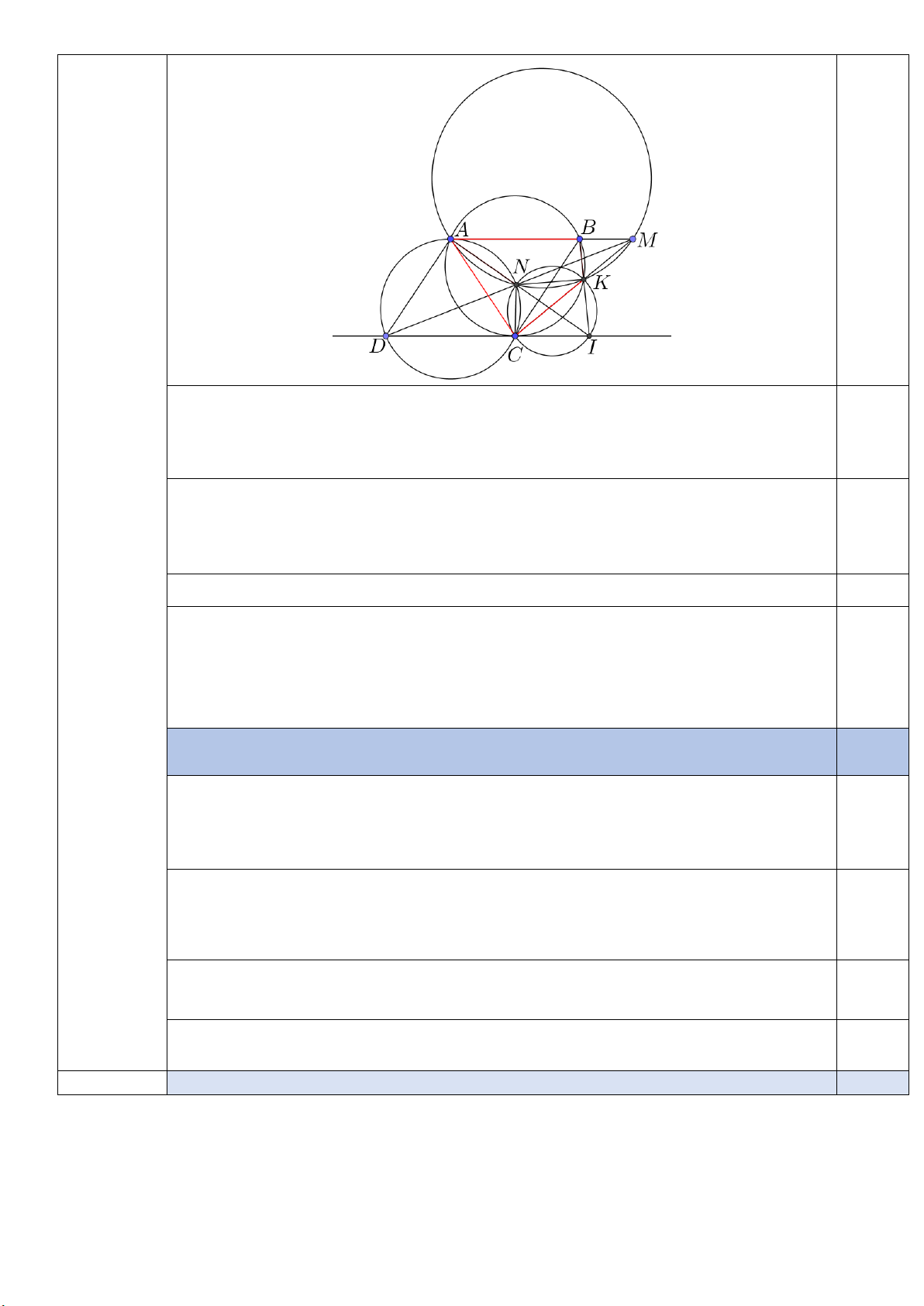
Câu 5 (2,0 điểm). Cho hình bình hành A BCD có CB  CA. Gọi M là điểm bất kỳ trên tia đối của
tia B A. Đường tròn ngoại tiếp tam giác A CD cắt MD tại N (N khác D), đường tròn ngoại tiếp
tam giác A MN cắt MC tại K (K khác M ).
a) Chứng minh tứ giác A BKC nội tiếp. Trang 1
b) Gọi I là giao điểm của đường thẳng A N và đường thẳng BK . Chứng minh I luôn thuộc
một đường thẳng cố định khi M thay đổi.
Câu 6 (0,5 điểm). Cho bảng ô vuông có kích thước 4  4 như hình sau:
Mỗi ô trong bảng này được viết một số nguyên dương sao cho 16 số trên bảng đôi một khác
nhau. Trong mỗi hàng, mỗi cột luôn tồn tại một số bằng tổng ba số còn lại trong hàng, trong cột đó.
Gọi M là số lớn nhất trong 16 số trên bảng. Tìm giá trị nhỏ nhất của M .
Câu 7 (1,0 điểm). Cho a, ,
b c là các số thực dương không nhỏ hơn 1. Chứng minh: ab  1 bc  1 ca  1
a  b  c    . b  c c  a a  b 4
----------HẾT----------
Ghi chú: Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh............................................. Số báo danh.... ..............................................
Chữ ký cán bộ coi thi 1.................................. Chữ ký cán bộ coi thi 2...................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT
THÀNH PHỐ CẦN THƠ NĂM HỌC 2023-2024
Khóa ngày 05 tháng 6 năm 2023 CHÍNH THỨC
ĐÁP ÁN - HƯỚNG DẪN CHẤM CHUYÊN MÔN TOÁN Câu Hướng dẫn giải Điểm 2 x  9 x  3 2 x  1 Cho biểu thức P   
với x  0 và x  4, x  9. x  5 x  6 x  2 3  x 1,0
a) Rút gọn biểu thức P . Câu 1 2 x  9 x  3 2 x  1
(1,5 điểm) P    x  5 x  6 x  2 3  x 0,25 2 x  9 x  3 2 x  1 P   
( x  2)( x  3) x  2 3  x Trang 2
2 x  9  ( x  3)( x  3)  (2 x  1)( x  2) P  0,25
( x  2)( x  3)
2 x  9  (x  9)  (2x  4 x  x  2) P    ( x 2)( x 3) 0,25
2 x  9  x  9  2x  4 x  x  2 x  x  2 P  
( x  2)( x  3)
( x  2)( x  3)
( x  2)( x  1) x  1 P   . 0,25
( x  2)( x  3) x  3
b) Tìm tất cả các số nguyên x sao cho P nhận giá trị là số chẵn. 0,5 x  3  4 4 Ta có P   1  x  3 x  3 0,25
P nhận giá trị là số chẵn khi x  3 là ước số của 4
Suy ra x  3  4  x  7  x  49 x  3  4   x  1  (loại) x  3  2 
x  5  x  25 x  3  2
  x  1  x  1 0,25
x  3  1  x  4  x  16 x  3  1
  x  2  x  4
Thử lại ta thấy P nhận giá trị chẵn khi x  49.
Trong mặt phẳng Oxy, cho đường thẳng d : y  2mx  4m  5, (m là tham số) và parabol 2
(P ) : y  x . Tìm tất cả giá trị của m để d cắt (P ) tại hai điểm phân biệt 1,0
A, B sao cho ba điểm O, A, B tạo thành tam giác vuông tại O .
Phương trình hoành độ giao điểm của (P ) và d 2
x  2mx  4m  5 0,25 2
 x  2mx  4m  5  0
Đường thẳng d cắt (P ) tại hai điểm phân biệt sao cho ba điểm O, A, B lập thành tam giác khi và chỉ khi 2
D '  m  4m  5  0 và x x  0 1 2 0,25 2 m
  4m  5  0 5 Hay   m  4m  5  0 4 Câu 2 
(1,0 điểm) Giả sử A(x ;y ),B(x ;y ) . 1 1 2 2 Đườ y
ng thẳng đi qua O, A có dạng y  ax , trong đó 1 a  là hệ số góc của x1 đường thẳng OA. 0,25 Tương tự y
hệ số góc của đường thẳng OB là 2 a '  x 2 Điề y y
u kiện để tam giác OA B vuông tại O là 1 2 .  1 x x 1 2 2 2 x x 1 2  .  1   x x  1 0,25 1 2 x x 1 2 Trang 3
Theo định lý Viet ta suy ra 4m  5  1
  m  1 (nhận) Vậy m  1.
Giải phương trình và hệ phương trình sau 1,0 a) 2 (x  3) x 
 8x  48  x  24. u   x  3 Đặ  t 
(điều kiện: u  0) 2 v  x   8x  48  0,25 2 2
ìï u = x + 6x + 9 ï 2 2  ï u   v  2  x  57 u   v  3 Þ í   2
 (u  v)  9   0,25 2 2
ï v = - x - 8x + 48 ï
2uv  2x  48 u  v  3  ïî  
TH1: u  v  3 x   0  2  0,25 x 
 8x  48  x     x  2   2 7 2
2x  8x  48  0 
TH2: u  v  3  x   6   2  x 
 x  48  x   6   2
2x  20x  12  0  0,25  x  5   31
Vậy tập nghiệm của phương trình là S   2   2 7; 5   3  1 . Câu 3 (2,0 điểm) 3 3 x
  y  35  0 a)  . 2 2 1,0
2x  3y  4x  9y  0  3 3 3 3 x
  y  35  0 x
  y  35  0 1()    2 2 2 2
2x  3y  4x  9y  0
6x  9y  12x  27y  0 (2)   0,25
Trừ vế theo vế (1) và (2), ta được 3 2 3 2
x  6x  12x  8  (y  9y  27y  27)  0 0,25 3 2 3 2
 x  6x  12x  8  y  9y  27y  27 3 3
 (x  2)  (y  3)
 x  2  y  3  y  x  5 Thay vào (2) ta được 2 2
2x + 3(x - 5) - 4x + 9(x - 5) = 0 0,25 x é = 3 2
5x - 25x + 30 = 0 ê Û x ê = 2 êë
Với x = 3 Þ y = - 2
Với x = 2 Þ y = - 3 0,25
Vậy hệ phương trình có hai nghiệm(x;y) là (3;- 2) và (2;- 3). Câu 4
a) Tìm tất cả các số nguyên x, y thỏa mãn 2 2
x  2y  xy  2x  5y  5  0. 1,0 (2,0 điểm) 2 2
x  2y  xy  2x  5y  5  0  (x  2y  3)(x  y  1)  2 0,25
Ta có các trường hợp sau x
  2y  3  2 x
  2y  3  1 x
  2y  3  2  x
  2y  3  1   ;     ;     ;          0,5 x y 1 1  x y 1 2  x y 1 1  x y 1 2 
Giải các hệ trên ta các cặp số nguyên (x;y) thỏa mãn là 1 ( ;1) và (2;1). 0,25 Trang 4
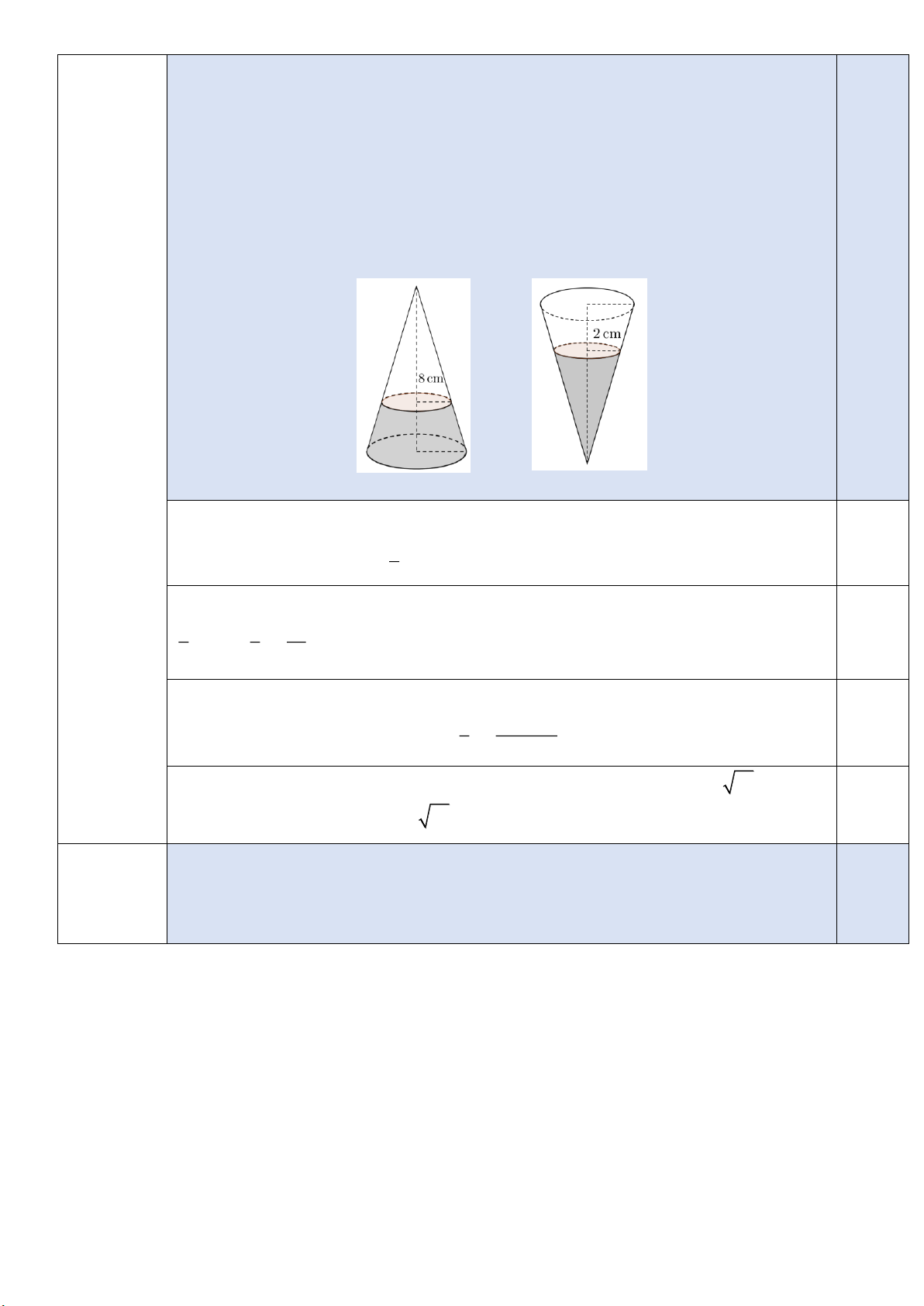
b) Một cái bình hình nón được đặt trên một mặt phẳng nằm ngang sao cho
đỉnh của nó hướng lên trên. Người ta rót nước vào bình cho đến khi mực
nước dâng cao cách đỉnh 8 cm (như hình 1 ). Sau đó, người ta đảo ngược
cái bình lại sao cho đỉnh bình hướng xuống (như hình 2 ). Khi đó, người
ta đo được phần không gian trống của bình có chiều cao 2 cm. Biết rằng
lượng nước trong bình không thay đổi. Tính chiều cao của hình nón đã cho. 1,0 Hình 1 Hình 2 Gọi h ( )
cm là chiều cao của bình nước, r (cm) là bán kính đáy của hình nón. 0,25 1
Thể tích của bình nước là 2 p r h. 3
Khi đặt bình nước có đỉnh hướng lên, thể tích của lượng nước là 2 1 1  8r  2 p r h  p   .8 (1) 0,25 3 3 h  
Khi úp bình xuống, lượng nước trên chiếm một thể tích bằng với thể tích hình 0,25 2 1
 (h  2)r 
nón có chiều cao là h  2 và bằng p   (h  2) (2) 3 h   Từ (1) và (2), suy ra 3 3 3
h  8  (h  2) 2
 h  2h  84  0  h  1  85 0,25
Vậy chiều cao của bình là 1  85 . cm
Cho hình bình hành A BCD có CB  CA. Gọi M là điểm bất kỳ trên tia đối của Câu 5
tia B A. Đường tròn ngoại tiếp tam giác A CD cắt MD tại N (N khác D), (2,0 điể 1,0
m) đường tròn ngoại tiếp tam giác A MN cắt MC tại K (K khác M ).
a) Chứng minh tứ giác A BKC nội tiếp. Trang 5
A BC  BA C (tam giác CAB cân, do CA = CB )
BA C  A CD (so le trong) 0,25
 ABC  ACD
A CDN nội tiếp  A CD  A ND (cùng chắn A D )  A BC  A ND
Mà A ND  MNI (đối đỉnh) 0,25
 ABC  MNI (1)
Mặt khác A KC  A KM  180 (kề bù) và MNI  A NM  180 (kề bù) 0,25 »
Mà A K M  A NM ( AMKN nội tiếp, cùng chắn A B )
Nên A KC  MNI (2) 0,25 ¼
Từ (1), (2), suy ra AKC  ABC (cùng nhìn A C )
Vậy A BKC nội tiếp.
b) Gọi I giao điểm của đường thẳng A N và đường thẳng BK . Chứng 1,0
minh I luôn thuộc một đường thẳng cố định khi M thay đổi.
Do I là giao điểm của A N và B K . Ta sẽ chứng minh C , D, I thẳng hàng. · · ·
ABKC nội tiếp Þ BA C = IKC (cùng bù với BKC ) 0,25 · · ·
A DCN nội tiếp Þ INC = A DC (cùng bù với A NC ) · ·
Mà BA C = A DC ( A BCD là hình bình hành có CA = CB ) · · » 0,25
Nên IKC = INC (cùng nhìn IC )
Þ Tứ giác CNIK nội tiếp.
Ta có CIA  CIN  CKN  180  MKN  MA N  MA I 0,25
Suy ra A M / / CI
Mà A M / / CD nên C , D, I thẳng hàng 0,25
Vậy I thuộc đường thẳng CD cố định khi M thay đổi. Câu 6
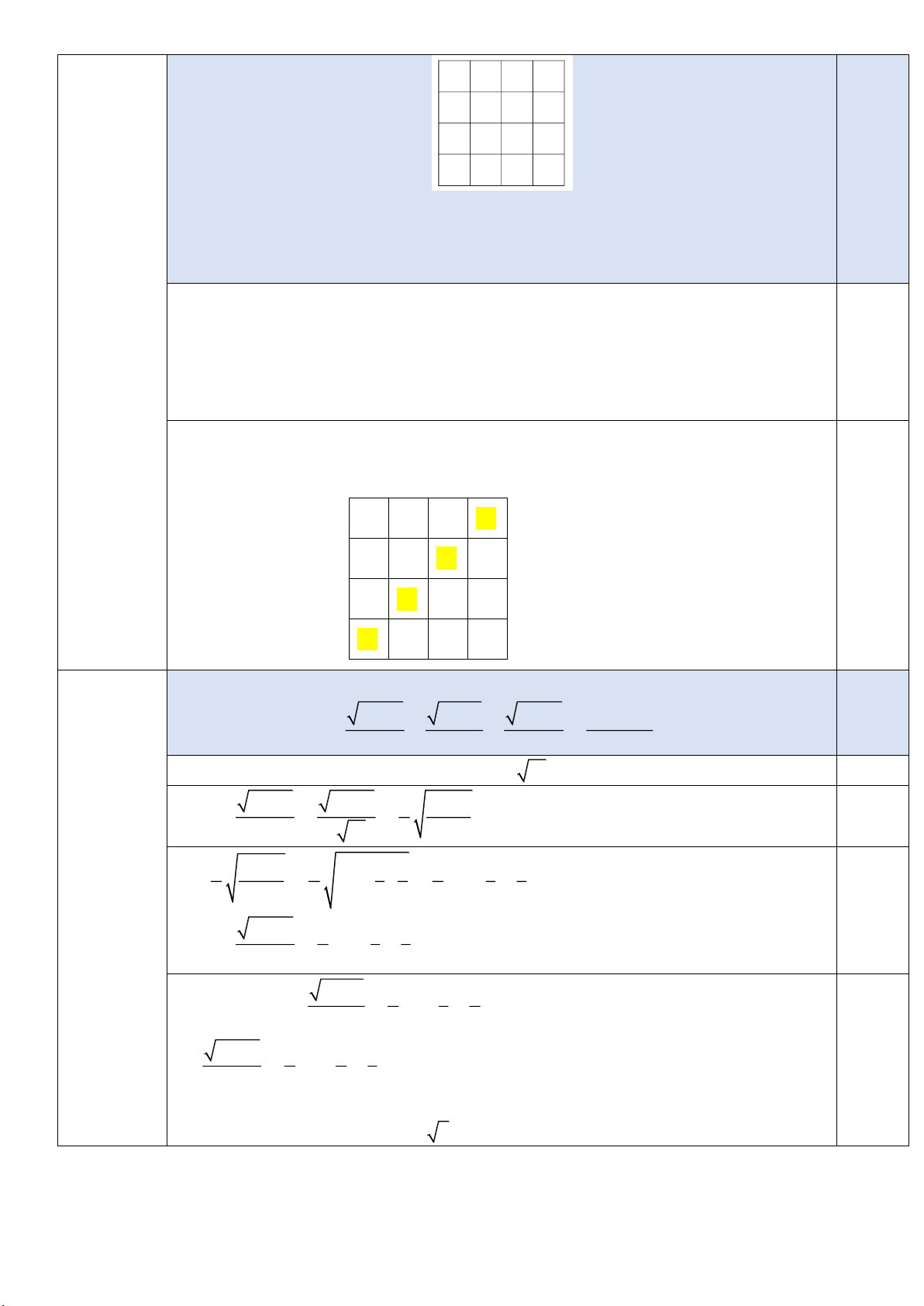
Cho bảng ô vuông 4  4 như hình sau: 0,5 Trang 6 (0,5 điểm)
Mỗi ô trong bảng này được viết một số nguyên dương sao cho 16 số trên bảng
đôi một khác nhau và trong mỗi hàng, mỗi cột luôn tồn tại một số bằng tổng ba
số còn lại trong hàng, cột đó. Gọi M là số lớn nhất trong 16 số đó. Tìm giá trị nhỏ nhất của M .
Gọi a ,a ,a ,a là các số lớn nhất trong các cột 1, 2, 3, 4 và gọi b ,b ,...,b là các 1 2 3 4 1 2 12
số trong các ô còn lại.
Khi đó a  a  a  a  b  b  ...  b . 0,25 1 2 3 4 1 2 12
Do các số trong 16 ô vuông đôi một khác nhau nên
b  b  ...  b  1  2  ...  12  78 1 2 12
và a  a  a  a  M  (M  1)  (M  2)  (M  3)  4M  6 1 2 3 4
Suy ra 4M  6  78  M  21.
Xây dựng một bảng ô vuông ứng với M  21 1 8 12 21 0,25 7 9 20 4 10 19 3 6 18 2 5 11 Cho a, ,
b c là các số thực dương không bé hơn 1. Chứng minh rằng ab  1 bc  1 ca  1
a  b  c 1,0    . b  c c  a a  b 4
Theo bất đẳng thức Cauchy ta có b  c  2 bc 0,25 ab  1 ab  1 1 ab  1 Suy ra   0,25 b  c 2 2 bc bc 1 ab  1 1  1  1 1  1 1  Mà 
a    a    Câu 7 2 bc 2 b c 4 b c     (1,0 điểm) 0,25 ab  1 1  1 1  Suy ra
 a    (1) b  c 4 b c      Tương tự bc 1 1 1 1 , ta có
 b    (2) c  a 4 c a   ca  1 1  1 1  và
 c    (3) 0,25 a  b 4 a b  
Cộng vế theo vế (1), (2) và (3), ta được đpcm.
Dấu “=” xảy ra khi a  b  c  2.
Chú ý: Mọi cách giải đúng khác đều được điểm tối đa. Trang 7