SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI TUYỂN SINH LỚP 10 THPT LẠNG SƠN
NĂM HỌC 2023 – 2024
Môn thi: Toán (dành cho lớp chuyên)
Thời gian làm bài: 150 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
Đề thi gồm có 02 trang, 05 câu Mã đề 181
Học sinh làm cả phần trắc nghiệm và tự luận vào tờ giấy thi, ghi rõ mã đề thi vào bên cạnh từ
Bài làm trên tờ giấy thi.
Câu 1: Trắc nghiệm (2,0 điểm, mỗi ý 0,25 điểm).
1. Tất cả các giá trị của m để hàm số y  m  
1 x  3 đồng biến trên là A. m  1  .
B. m  0 . C. m  1  .
D. m  0 .
2. Cho tam giác ABC vuông cân tại A , biết BC  8cm . Diện tích tam giác ABC bằng A. 2 16 cm . B. 2 8cm . C. 2 64 cm . D. 2 32 cm .
3. Cho tứ giác ABCD nội tiếp đường tròn, giả sử số đo góc 0
BAC  50 thì số đo góc BDC là A. 0 40 . B. 0 100 . C. 0 130 . D. 0 50 . x  y  3
4. Biết  x ; y là nghiệm của hệ phương trình 
. Khi đó giá trị biểu thức x  y là 0 0 
2x  3y 1 0 0 3 1 A. . B. 3 . C. 2 . D. . 2 2
5. Cho đường tròn có bán kính bằng 2 , chu vi của đường tròn đó là A. 2 . B. 2 . C. 4 . D. 4 .
6. Tất cả các giá trị của tham số m để đường thẳng d  : y  2x  m cắt parabol  P 2
: y  x tại hai điểm phân biệt là A. m 1. B. m  1  . C. m  1  .
D. m 1.
7. Tổng các nghiệm của phương trình x  3 x  2  0 là A. 3 . B. 2 . C. 4 . D. 5 .
8. Biểu thức P 
4  2x có nghĩa khi
A. x  2 . B. x  2  . C. x  2  .
D. x  2 . Câu 2 (1,5 điểm). 3  2x 1 x   1 x 
a) Rút gọn biểu thức A    . x    
, với x  0, x  1. 3  
 x 1 x  x 1 1 x   
b) Giải phương trình x  2  3x  2  2x  4 . 2 2
x  2y  xy 3x  3y  0
c) Giải hệ phương trình  . 2 2
x  y  x  y  4  0 Trang 1
Câu 3 (1,5 điểm). Cho các số thực dương ,
x y, z thỏa mãn x  y  z  3 . Chứng minh các bất đẳng thức sau đây: a) 2 2 2
x  y  z  3 ; 3 b) 2 2 2
 x  y  z  4 ; 2 2 2
x  y  z
c) xy  yz  zx  3 xyz .
Câu 4 (3,0 điểm). Cho tam giác ABC không cân, có ba góc nhọn và AB  AC . Đường tròn tâm I
nội tiếp tam giác ABC tiếp xúc với ba cạnh BC, C ,
A AB lần lượt tại D, E, F . Lấy S trên đường
thẳng EF sao cho AS // BC , gọi DI  AS  H .
a) Chứng minh rằng 5 điểm ,
A F , I , E, H nằm trên cùng một đường tròn và đường thẳng HI là
phân giác của FHE .
b) Gọi DI  EF  K . Đường thẳng đi qua K và song song với BC cắt AB, AC lần lượt tại
P, Q . Chứng minh rằng tam giác IPQ cân và đường thẳng AK đi qua trung điểm của BC .
c) Kẻ DI cắt lại đường tròn nội tiếp ABC 
ở T . Chứng minh rằng ST  AD . Câu 5 (2,0 điểm).
a) Tìm tất cả các cặp số nguyên  ;
x y thỏa mãn phương trình 2
x  5x  6y  3xy 1  0 .
b) Cho biết Định lí Fermat nhỏ: “Cho số nguyên tố p . Nếu số nguyên x không chia hết cho p  thì p 1 x
1mod p, hay là p 1
x  1 p ”.
1) Chứng minh rằng với mọi số nguyên a thì 5 a  a 5 .
2) Cho hai số nguyên a, b . Gọi p  4k  3 ( k 
) là số nguyên tố và p là ước của 2 2 a  b .
Chứng minh rằng p là ước chung của a và b .
c) Cho tập hợp S gồm 2023 điểm trên mặt phẳng sao cho không có ba điểm nào thẳng hàng,
không có bốn điểm nào nằm trên cùng một đường tròn. Chứng minh rằng tồn tại ba điểm , A B, C
thuộc tập S sao cho: bên trong đường tròn ngoại tiếp ABC 
có đúng 674 điểm của tập S .
----------------------Hết--------------------------
Họ và tên thí sinh:…………………………………….SBD:………………………….
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI TUYỂN SINH LỚP 10 THPT LẠNG SƠN
NĂM HỌC 2023 – 2024
Môn thi: Toán (dành cho lớp chuyên)
Thời gian làm bài: 150 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
Đề thi gồm có 02 trang, 05 câu Mã đề 235
Học sinh làm cả phần trắc nghiệm và tự luận vào tờ giấy thi, ghi rõ mã đề thi vào bên cạnh từ
Bài làm trên tờ giấy thi. Trang 2
Câu 1: Trắc nghiệm (2,0 điểm, mỗi ý 0,25 điểm).
1. Biểu thức P  1 x có nghĩa khi A. x  1  . B. x  1  .
C. x 1.
D. x 1.
2. Tổng các nghiệm của phương trình x  4 x  3  0 là A. 3 . B. 2 . C. 10 . D. 4 .
3. Cho tam giác ABC vuông cân tại A , biết BC  6 cm . Diện tích tam giác ABC bằng A. 2 9cm . B. 2 18cm . C. 2 6cm . D. 2 36cm .
4. Cho tứ giác ABCD nội tiếp đường tròn, giả sử số đo góc 0
BAC  60 thì số đo góc BDC là A. 0 150 . B. 0 60 . C. 0 30 . D. 0 120 .
5. Cho đường tròn có bán kính bằng 5 , chu vi của đường tròn đó là A. 10 . B. 10 . C. 25 . D. 25 .
6. Tất cả các giá trị của m để hàm số y  m  2 x 1 đồng biến trên là
A. m  0 . B. m  2  .
C. m  0. D. m  2  .
7. Tất cả các giá trị của tham số m để đường thẳng d  : y  4x  m cắt parabol  P 2
: y  x tại hai điểm phân biệt là
A. m  4.
B. m  4 . C. m  4  . D. m  4  .
x  2y  6
8. Biết  x ; y là nghiệm của hệ phương trình 
. Khi đó giá trị biểu thức x  y là 0 0  3
 x  y  4 0 0 A. 0 . B. 2 . C. 4 . D. 1. Câu 2 (1,5 điểm). 3  2x 1 x   1 x 
a) Rút gọn biểu thức A    . x    
, với x  0, x  1. 3  
 x 1 x  x 1 1 x   
b) Giải phương trình x  2  3x  2  2x  4 . 2 2
x  2y  xy 3x  3y  0
c) Giải hệ phương trình  . 2 2
x  y  x  y  4  0
Câu 3 (1,5 điểm). Cho các số thực dương ,
x y, z thỏa mãn x  y  z  3 . Chứng minh các bất đẳng thức sau đây: a) 2 2 2
x  y  z  3 ; 3 b) 2 2 2
 x  y  z  4 ; 2 2 2
x  y  z
c) xy  yz  zx  3 xyz .
Câu 4 (3,0 điểm). Cho tam giác ABC không cân, có ba góc nhọn và AB  AC . Đường tròn tâm I
nội tiếp tam giác ABC tiếp xúc với ba cạnh BC, C ,
A AB lần lượt tại D, E, F . Lấy S trên đường
thẳng EF sao cho AS // BC , gọi DI  AS  H .
a) Chứng minh rằng 5 điểm ,
A F , I , E, H nằm trên cùng một đường tròn và đường thẳng HI là
phân giác của FHE . Trang 3
b) Gọi DI  EF  K . Đường thẳng đi qua K và song song với BC cắt AB, AC lần lượt tại
P, Q . Chứng minh rằng tam giác IPQ cân và đường thẳng AK đi qua trung điểm của BC .
c) Kẻ DI cắt lại đường tròn nội tiếp ABC 
ở T . Chứng minh rằng ST  AD . Câu 5 (2,0 điểm).
a) Tìm tất cả các cặp số nguyên  ;
x y thỏa mãn phương trình 2
x  5x  6y  3xy 1  0 .
b) Cho biết Định lí Fermat nhỏ: “Cho số nguyên tố p . Nếu số nguyên x không chia hết cho p  thì p 1 x
1mod p, hay là p 1
x  1 p ”.
1) Chứng minh rằng với mọi số nguyên a thì 5 a  a 5 .
2) Cho hai số nguyên a, b . Gọi p  4k  3 ( k 
) là số nguyên tố và p là ước của 2 2 a  b .
Chứng minh rằng p là ước chung của a và b .
c) Cho tập hợp S gồm 2023 điểm trên mặt phẳng sao cho không có ba điểm nào thẳng hàng,
không có bốn điểm nào nằm trên cùng một đường tròn. Chứng minh rằng tồn tại ba điểm , A B, C
thuộc tập S sao cho: bên trong đường tròn ngoại tiếp ABC 
có đúng 674 điểm của tập S .
----------------------Hết--------------------------
Họ và tên thí sinh:…………………………………….SBD:………………………….
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI TUYỂN SINH LỚP 10 THPT LẠNG SƠN
NĂM HỌC 2023 – 2024
Môn thi: Toán (dành cho lớp chuyên)
Thời gian làm bài: 150 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
Đề thi gồm có 02 trang, 05 câu Mã đề 316
Học sinh làm cả phần trắc nghiệm và tự luận vào tờ giấy thi, ghi rõ mã đề thi vào bên cạnh từ
Bài làm trên tờ giấy thi.
Câu 1: Trắc nghiệm (2,0 điểm, mỗi ý 0,25 điểm).
1. Cho tứ giác ABCD nội tiếp đường tròn, giả sử số đo góc 0
BAC  70 thì số đo góc BDC là A. 0 110 . B. 0 70 . C. 0 20 . D. 0 160 .
2. Biểu thức P  3  x có nghĩa khi
A. x  3. B. x  3  .
C. x  3. D. x  3  .
3. Tổng các nghiệm của phương trình x  5 x  6  0 là A. 2 . B. 3 . C. 13 . D. 5 .
4. Tất cả các giá trị của m để hàm số y  m  3 x 1 đồng biến trên là A. m  3  . B. m  3  .
C. m  0 .
D. m  0 . x  y  1
5. Biết  x ; y là nghiệm của hệ phương trình 
. Khi đó giá trị biểu thức x  y là 0 0 
2x  y  8 0 0 Trang 4 A. 5 . B. 1. C. 9 . D. 6 .
6. Cho đường tròn có bán kính bằng 3 , chu vi của đường tròn đó là A. 6 . B. 6 . C. 9 . D. 9 .
7. Cho tam giác ABC vuông cân tại A , biết BC  4 cm . Diện tích tam giác ABC bằng A. 2 8cm . B. 2 4cm . C. 2 12cm . D. 2 16cm .
8. Tất cả các giá trị của tham số m để đường thẳng d  : y  2x  m cắt parabol  P 2
: y  x tại hai điểm phân biệt là A. m 1. B. m  1  . C. m  1  . D. m 1. Câu 2 (1,5 điểm). 3  2x 1 x   1 x 
a) Rút gọn biểu thức A    . x    
, với x  0, x  1. 3  
 x 1 x  x 1 1 x   
b) Giải phương trình x  2  3x  2  2x  4 . 2 2
x  2y  xy 3x  3y  0
c) Giải hệ phương trình  . 2 2
x  y  x  y  4  0
Câu 3 (1,5 điểm). Cho các số thực dương ,
x y, z thỏa mãn x  y  z  3 . Chứng minh các bất đẳng thức sau đây: a) 2 2 2
x  y  z  3 ; 3 b) 2 2 2
 x  y  z  4 ; 2 2 2
x  y  z
c) xy  yz  zx  3 xyz .
Câu 4 (3,0 điểm). Cho tam giác ABC không cân, có ba góc nhọn và AB  AC . Đường tròn tâm I
nội tiếp tam giác ABC tiếp xúc với ba cạnh BC, C ,
A AB lần lượt tại D, E, F . Lấy S trên đường
thẳng EF sao cho AS // BC , gọi DI  AS  H .
a) Chứng minh rằng 5 điểm ,
A F , I , E, H nằm trên cùng một đường tròn và đường thẳng HI là
phân giác của FHE .
b) Gọi DI  EF  K . Đường thẳng đi qua K và song song với BC cắt AB, AC lần lượt tại
P, Q . Chứng minh rằng tam giác IPQ cân và đường thẳng AK đi qua trung điểm của BC .
c) Kẻ DI cắt lại đường tròn nội tiếp ABC 
ở T . Chứng minh rằng ST  AD . Câu 5 (2,0 điểm).
a) Tìm tất cả các cặp số nguyên  ;
x y thỏa mãn phương trình 2
x  5x  6y  3xy 1  0 .
b) Cho biết Định lí Fermat nhỏ: “Cho số nguyên tố p . Nếu số nguyên x không chia hết cho p  thì p 1 x
1mod p, hay là p 1
x  1 p ”.
1) Chứng minh rằng với mọi số nguyên a thì 5 a  a 5 . Trang 5
2) Cho hai số nguyên a, b . Gọi p  4k  3 ( k 
) là số nguyên tố và p là ước của 2 2 a  b .
Chứng minh rằng p là ước chung của a và b .
c) Cho tập hợp S gồm 2023 điểm trên mặt phẳng sao cho không có ba điểm nào thẳng hàng,
không có bốn điểm nào nằm trên cùng một đường tròn. Chứng minh rằng tồn tại ba điểm , A B, C
thuộc tập S sao cho: bên trong đường tròn ngoại tiếp ABC 
có đúng 674 điểm của tập S .
----------------------Hết--------------------------
Họ và tên thí sinh:…………………………………….SBD:………………………….
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI TUYỂN SINH LỚP 10 THPT LẠNG SƠN
NĂM HỌC 2023 – 2024
Môn thi: Toán (dành cho lớp chuyên)
Thời gian làm bài: 150 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
Đề thi gồm có 02 trang, 05 câu Mã đề 479
Học sinh làm cả phần trắc nghiệm và tự luận vào tờ giấy thi, ghi rõ mã đề thi vào bên cạnh từ
Bài làm trên tờ giấy thi.
Câu 1: Trắc nghiệm (2,0 điểm, mỗi ý 0,25 điểm).
1. Cho đường tròn có bán kính bằng 4 , chu vi của đường tròn đó là A. 8 . B. 8 . C. 16 . D. 16 .
2. Cho tứ giác ABCD nội tiếp đường tròn, giả sử số đo góc 0
BAC  55 thì số đo góc BDC là A. 0 125 . B. 0 35 . C. 0 55 . D. 0 110 .
3. Biểu thức P  5  x có nghĩa khi
A. x  5.
B. x  5. C. x  5  . D. x  5  .
4. Cho tam giác ABC vuông cân tại A , biết BC  2cm. Diện tích tam giác ABC bằng A. 2 4cm . B. 2 1cm . C. 2 8cm . D. 2 2cm . x  y  4
5. Biết  x ; y là nghiệm của hệ phương trình 
. Khi đó giá trị biểu thức x  y là 0 0 
2x  y  2 0 0 3 3 A.  . B. . C. 0 . D. 1. 2 2
6. Tất cả các giá trị của tham số m để đường thẳng d  : y  6x  m cắt parabol  P 2
: y  x tại hai điểm phân biệt là
A. m  9 .
B. m  9 .
C. m  9 .
D. m  9 .
7. Tất cả các giá trị của m để hàm số y  m  3 x 1 đồng biến trên
A. m  3 .
B. m  0 .
C. m  0 .
D. m  3 .
8. Tổng các nghiệm của phương trình x  6 x  8  0 là A. 20 . B. 2 . C. 6 . D. 4 . Trang 6 Câu 2 (1,5 điểm). 3  2x 1 x   1 x 
a) Rút gọn biểu thức A    . x    
, với x  0, x  1. 3  
 x 1 x  x 1 1 x   
b) Giải phương trình x  2  3x  2  2x  4 . 2 2
x  2y  xy 3x  3y  0
c) Giải hệ phương trình  . 2 2
x  y  x  y  4  0
Câu 3 (1,5 điểm). Cho các số thực dương ,
x y, z thỏa mãn x  y  z  3 . Chứng minh các bất đẳng thức sau đây: a) 2 2 2
x  y  z  3 ; 3 b) 2 2 2
 x  y  z  4 ; 2 2 2
x  y  z
c) xy  yz  zx  3 xyz .
Câu 4 (3,0 điểm). Cho tam giác ABC không cân, có ba góc nhọn và AB  AC . Đường tròn tâm I
nội tiếp tam giác ABC tiếp xúc với ba cạnh BC, C ,
A AB lần lượt tại D, E, F . Lấy S trên đường
thẳng EF sao cho AS // BC , gọi DI  AS  H .
a) Chứng minh rằng 5 điểm ,
A F , I , E, H nằm trên cùng một đường tròn và đường thẳng HI là
phân giác của FHE .
b) Gọi DI  EF  K . Đường thẳng đi qua K và song song với BC cắt AB, AC lần lượt tại
P, Q . Chứng minh rằng tam giác IPQ cân và đường thẳng AK đi qua trung điểm của BC .
c) Kẻ DI cắt lại đường tròn nội tiếp ABC 
ở T . Chứng minh rằng ST  AD . Câu 5 (2,0 điểm).
a) Tìm tất cả các cặp số nguyên  ;
x y thỏa mãn phương trình 2
x  5x  6y  3xy 1  0 .
b) Cho biết Định lí Fermat nhỏ: “Cho số nguyên tố p . Nếu số nguyên x không chia hết cho p  thì p 1 x
1mod p, hay là p 1
x  1 p ”.
1) Chứng minh rằng với mọi số nguyên a thì 5 a  a 5 .
2) Cho hai số nguyên a, b . Gọi p  4k  3 ( k 
) là số nguyên tố và p là ước của 2 2 a  b .
Chứng minh rằng p là ước chung của a và b .
c) Cho tập hợp S gồm 2023 điểm trên mặt phẳng sao cho không có ba điểm nào thẳng hàng,
không có bốn điểm nào nằm trên cùng một đường tròn. Chứng minh rằng tồn tại ba điểm , A B, C
thuộc tập S sao cho: bên trong đường tròn ngoại tiếp ABC 
có đúng 674 điểm của tập S .
----------------------Hết--------------------------
Họ và tên thí sinh:…………………………………….SBD:…………………………. Trang 7
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI TUYỂN SINH LỚP 10 THPT LẠNG SƠN
NĂM HỌC 2023 – 2024
Môn thi: Toán (dành cho lớp chuyên)
Hướng dẫn chấm gồm có 04 trang HDC CHÍNH THỨC Hướng dẫn chung:
- Học sinh có thể giải theo những cách khác nhau, nếu đúng thì giám khảo vẫn cho điểm tối đa ứng với phần đó.
- Đối với bài hình học: Nếu học sinh không vẽ hình, hoặc vẽ hình sai hẳn: không cho điểm.
- Điểm toàn bài chấm lẻ đến 0,25.
Câu 1: Trắc nghiệm (2,0 điểm) Đáp án các mã đề Ý Điểm Mã đề 181 Mã đề 235 Mã đề 316 Mã đề 479 1 C C B B 0,25 2 A C A C 0,25 3 D A C B 0,25 4 B B B B 0,25 5 C B A C 0,25 6 C D B C 0,25 7 D C B A 0,25 8 A C D A 0,25 Câu 2 (1,5 điểm) Ý Nội dung Điểm 3      2x 1 x   x  x x x 1 2 1 1 A    . x   
. x  1 x  x    0,25 3    
 x 1 x  x 1 1 x     x  
1  x  x     1 a x  x 1     0,25
x   x  x   . x 1 1 1 1 ĐK: 2 x  3
x  23x  2   0,25 pt 
 2x  4   x   1 2 4 1  0   b
x  2  3x  2
 x  2  3x  2  2x  4  0   1    (tmđk)  x 2 0,25 1  0 VN 
 3x  2  x  2 2 2
x  2y  xy  3x  3y  0    1  2 2 c
x  y  x  y  4  0  2   x  y
1   x  y x  2y  3  0   0,25
x  3  2y Trang 8
 y 1 x  1
Với x  y , thay vào 2 ta được: 2
2 y  2 y  4  0    y  2   x  2 
 y 1 x 1
Với x  3  2y , thay vào 2 ta được: 2 
5y 13y  8  0  8 1  0,25 y   x    5 5   
Vậy nghiệm của hệ phương trình là  x y       1 8 ; 1;1 ; 2; 2 ;  ;   .   5 5  Câu 3 (1,5 điểm) Ý Nội dung Điểm
Áp dụng bất đẳng thức Cô-si ta có 2 2 2 x 1  2 ; x y 1  2 ;
y z 1  2z 0,25
Cộng các bất đẳng thức vế theo vế ta được a 2 2 2
x  y  z    x  y  z 2 2 2 3 2
 x  y  z  3  6 2 2 2
 x  y  z  3, dấu bằng 0,25
xảy ra khi và chỉ khi x  y  z  1. Đặt 3 2 2 2
t  x  y  z  3 , bất đẳng thức 2 2 2
 x  y  z  4 trở thành 2 2 2
x  y  z b 0,25 3 2 2
 t  4  3 t  4t  t  4t  3  0  t   1 3  0 t
Bất đẳng này đúng đúng vì t  3 , dấu bằng xảy ra khi vả chỉ khi x  y  z  1. 0,25
xy  yz  zx  3 xyz   xy  yz  zx2  9xyz 0,25 2 2 2 2 2 2
 x y  y z  z x  2xyz x  y  z 2 2 2 2 2 2
 9xyz  x y  y z  z x  3xyz Áp dụng BĐT Cô-si ta có c 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2       x y y z 2xy z; y z z x 2xyz ; z x x y 2x yz
Cộng các bất đẳng thức trên trên vế theo vế ta được 0,25 2 2 2 2 2 2
x y  y z  z x  xyz  x  y  z  3xyz
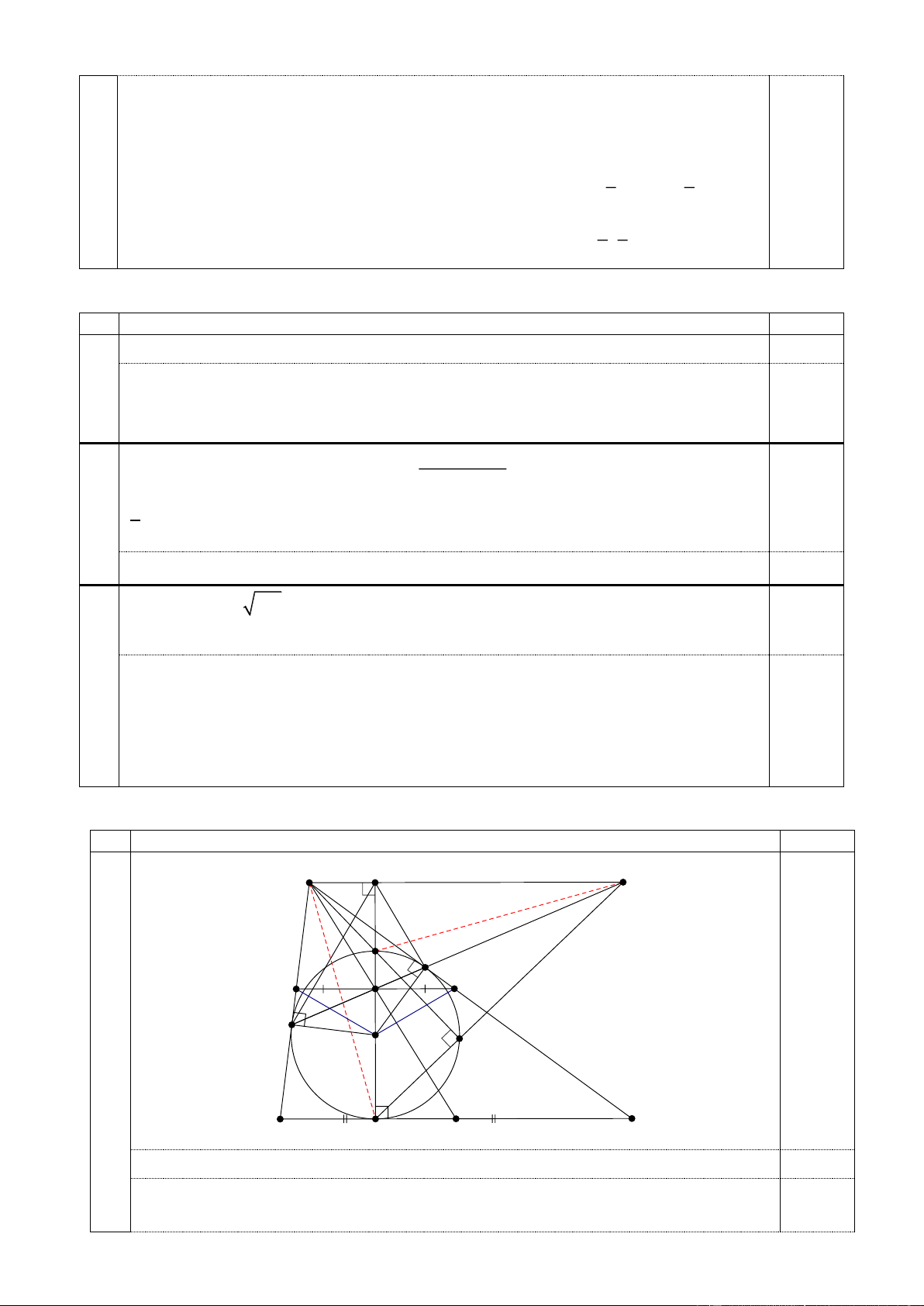
Dấu bằng xảy ra khi và chỉ khi x  y  z  1. Câu 4 (3,0 điểm) Ý Nội dung Điểm A H S E T P Q K F a L I B D M C Dễ thấy rằng   90o AFI AEI nên  180o AFI AEI
suy ra AFIE nội tiếp. 0,25
Vì AS // BC và DI  BC , suy ra AH  HI , vậy thì  180o AFI AHI 0,25
suy ra AHIF nội tiếp, vậy thì 5 điểm ,
A H , E, I , F nằm trên đường tròn. Trang 9 1 1 Suy ra FHI  sd IF; EHI  sd IE; 0,25 2 2
Lại có IE  IF (bán kính đường tròn nội tiếp); do đó suy ra FHI  EHI , hay là HI 0,25
là phân giác góc FHE .
Vì PQ // BC suy ra PQ  IK . Dễ thấy   90o IKQ IEQ
nên KEQI nội tiếp, do đó 0,25 IQK  IEK .
Chứng minh tương tự thì IPK  IFK , chú ý rằng tam giác IEF cân tại I nên suy ra 0,25 b
IQK  IPK nên IP  IQ .
Gọi M là trung điểm của đoạn BC . 0,25
Vì tam giác IPQ cân và có IK là đường cao nên suy ra KP  KQ . KP MB
Vì PQ // BC và có 
 1, theo định lí Thales đảo thì ,
A K , M thẳng hàng. 0,25 KQ MC
Gọi SD I   L , dễ thấy rằng S . E SF  S .
L SD (vì EFLD nội tiếp). 0,25
Lại có AFIEH nội tiếp nên S . E SF  S .
A SH , suy ra S . L SD  S .
A SH tức là AHLD 0,25 nội tiếp, suy ra 90o ALD  . c
Vì DT là đường kính của  I  nên 90o TLD  , do đó ,
A T , L thẳng hàng 0,25
Xét tam giác ADS có DH  SA , AL  SD suy ra T là trực tâm tam giác ADS . Do đó suy ra 0,25 ST  AD Câu 5 (2,0 điểm) Ý Nội dung Điểm 2
x  5x  6y  3xy 1  0   x  2 x  3y  3  5 0,25 x  2 1 5 1 5  x  3 y  3 5 1 5  1 x 1 3 3  7  a 0,25 5 5 y 1   1 3 3 Kết luận t/m Loại t/m Loại
Vậy phương trình có các nghiệm nguyên  ; x y   1  ;  1 ; 7  ;  1  . 0,25
1) Nếu a 5 thì 5 a  a 5 ; Nếu 0,25
a  5 , áp dụng định lí Fermat thì 4 a 1 5 , do đó 5
a  a  a  4 a   1 5 .
2) Nếu a p , vì 2 2
a  b chia hết cho p nên 2 b p  b p
vậy thì p là ước chung của a và b .
Giả sử, a  p , vì 2 2
a  b chia hết cho p nên 2
b  p  b  p . p 1 0,25 Từ 2 2 a  b   p 2 2 0 mod  a  b
 mod p, chú ý rằng
 2k 1 là số lẻ, b 2 p 1  p 1  do đó  2 a    2 b   p  p 1  p 1  2 2 mod  a  b mod p (*) p 1 a  1  mod p
theo định lí Fermat thì  (**) p 1 b   1  mod p
Từ (*) và (**) thì ta suy ra 1  1
 mod p  2  0mod p hay là 2 p 0,25
điều này vô lí vì p là số lẻ.
Do đó điều giả sử sai, tức là ,
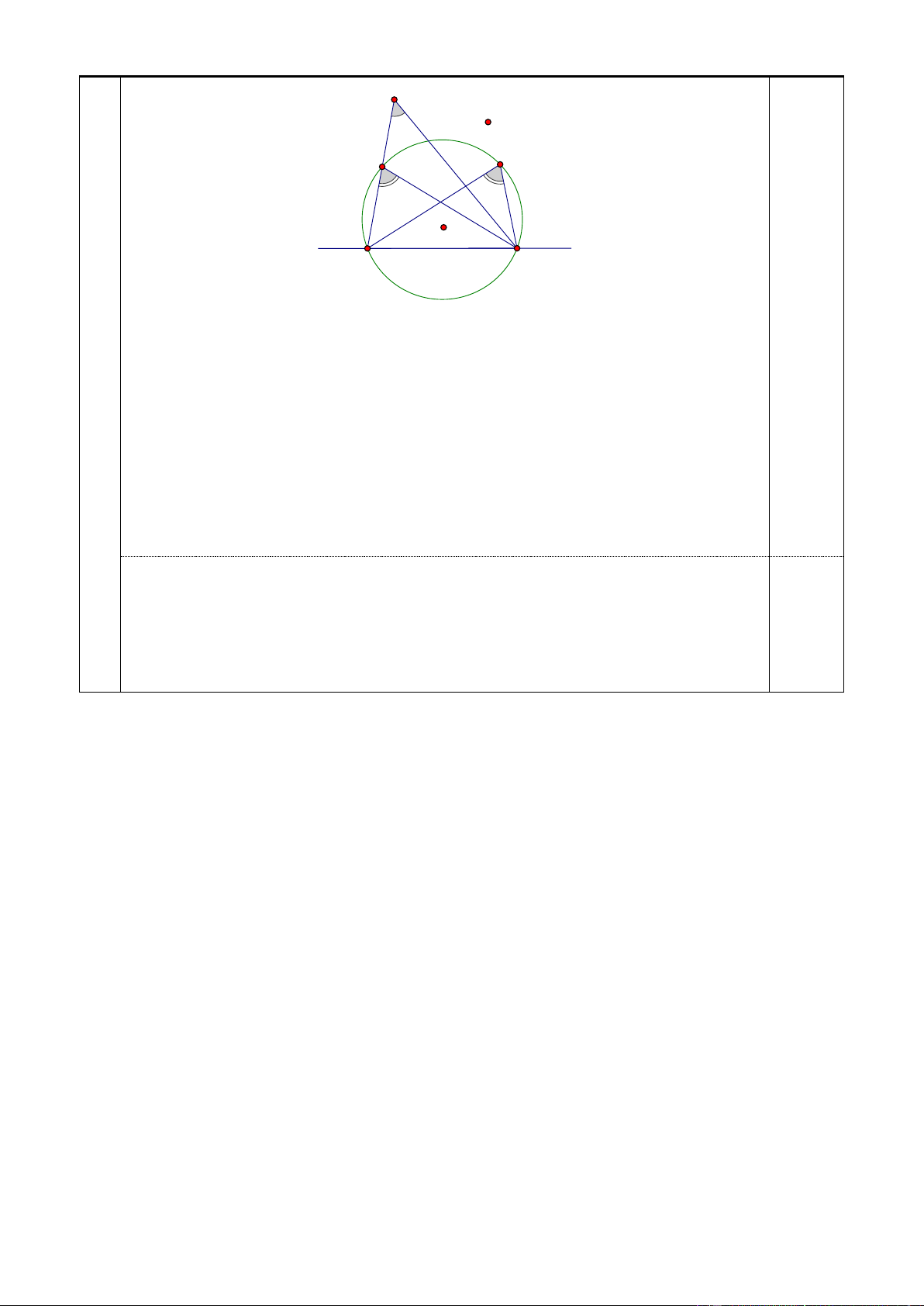
a b p hay là p là ước chung của a và b . Trang 10 Xn+1 X1 M Xn X1012 A B Lấy 2 điểm ,
A B sao cho tất cả các điểm của tập S nằm về cùng một phía của 0,25 đường thẳng AB . Nhận xét: c
Với điểm X và X n n 1
 bất kì. Xét đường tròn ngoại tiếp tam giác
ABX (như hình vẽ). Thế thì: X n n 1
 ở ngoài đường tròn này khi và chỉ khi AX B  AX B . n 1  n
Chứng minh nhận xét: X ABX khi và n 1
 ở ngoài đường tròn ngoại tiếp tam giác n
chỉ khi một trong hai đường AX , BX ABX
như hình vẽ, giả sử BX n 1  n 1  cắt  n  n 1 
cắt tại M . Khi đó, theo tính chất góc ngoài tam giác thì AX B  AMB  AX B n 1  n
(các trường hợp hình vẽ suy biến khác có thể lập luận tương tự).
Vì 4 điểm bất kì không nằm trên đường tròn, do đó ta đánh số các điểm còn lại của tập S (trừ ,
A B ) là X , X ,..., X sao cho 1 2 2021
AX B  AX B  ....  AX B  AX B  ...  AX B . 0,25 1 2 674 675 2021
Chọn đường tròn  AX B , thì có đúng các điểm X , X ,..., X nằm trong 675  1 2 674 đường tròn này.
------------ HẾT ------------- Trang 11