Đề thi tuyển sinh vào lớp 10 THPT năm học 2023-2024 môn toán Sở GD Hòa Bình (có đáp án và lời giải chi tiết)

SỞ GD&ĐT HÒA BÌNH KỲ THI TUYỂN SINH VÀO LỚP 10 TRUNG HỌC PHỔ THÔNG
NĂM HỌC 2023 – 2024 ĐỀ THI MÔN TOÁN ĐỀ CHÍNH THỨC
(Dành cho thí sinh dự thi vào lớp chuyên Toán) THUC Ngày thi: 07/6/2023
Thời gian làm bài: 150 phút, không kể thời gian giao đề.
Đề thi có 01 trang, gồm 04 câu.
-------------------------------------------------------------------------------------------------------
Câu I (3,0 điểm)
1. Rút gọn biểu thức: A  ( 5 1) 6  2 5
2. Gọi x ; x là hai nghiệm của phương trình 2
x  x  3  0. Không giải phương trình, 1 2 x x
hãy tính giá trị biểu thức: 1 2 B   x x 2 1
3. Trong mặt phẳng tọa độ Oxy , cho đường thẳng (d) : y  (m  2)x  3 . Tìm giá trị
của m để đường thẳng (d) cắt hai trục O ;
x Oy lần lượt tại 2 điểm A và B sao cho tam giác AOB cân.
Câu II (3,0 điểm) 1. Giải phương trình: 2 2 2
(4x  7x  4)(3x  4x  3)  3x
x  my  3m  3
2. Cho hệ phương trình: 
(m là tham số). Tìm các giá trị nguyên
mx  y  2m  2
của m để hệ phương trình có nghiệm duy nhất ( ;
x y) , trong đó ;
x y là các số nguyên.
3. Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Một con Robot được lập trình để chuyển động thẳng đều trên một quãng đường từ điểm
A đến điểm B theo quy tắc: Đi được 120cm thì dừng lại 1 phút, đi tiếp 240cm rồi dừng lại 2
phút, đi tiếp 360cm rồi dừng lại 3 phút..., tổng thời gian từ khi bắt đầu di chuyển từ A cho đến
B là 253 phút. Tính quãng đường từ A đến B biết vận tốc của Robot không đổi là 40cm/phút.
Câu III (3,0 điểm)
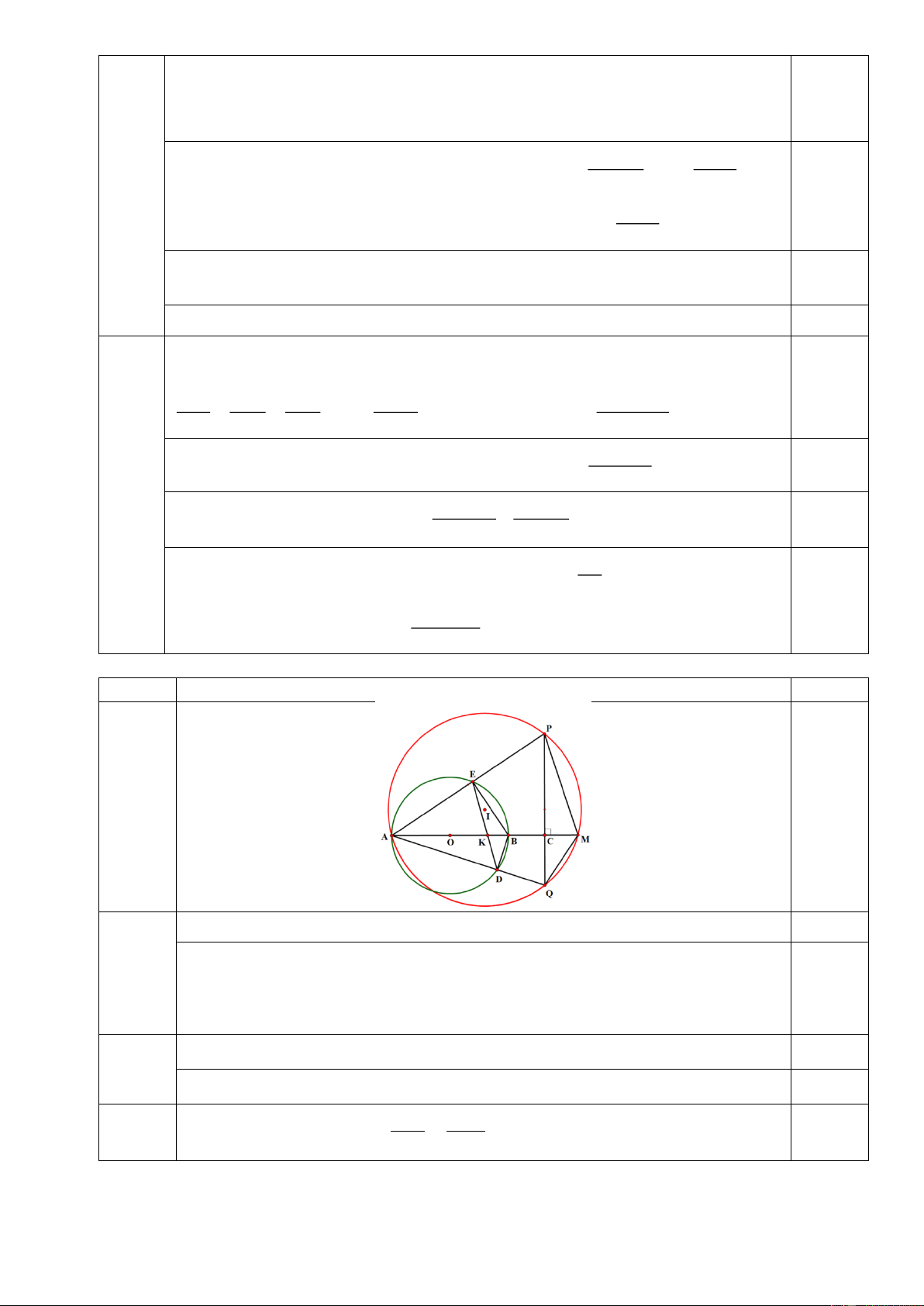
Cho đường tròn tâm O , đường kính AB cố định. Trên tia đối của tia BA lấy điểm
C cố định, qua C kẻ đường thẳng d vuông góc với AC . Gọi K là điểm cố định nằm giữa
O và B (K khác O và B) , qua K vẽ dây cung ED bất kì của đường tròn (O) . Gọi , P Q
lần lượt là giao điểm của AE và AD với đường thẳng d . Đường tròn ngoại tiếp tam giác
APQ cắt tia AC tại điểm M (M khác )
A . Chứng minh rằng:
a) Tứ giác PEDQ nội tiếp được trong một đường tròn.
b) ° AKD ” ° AQM.
c) AK.AM  A . B A . C
d) Khi dây ED thay đổi thì tâm đường tròn ngoại tiếp tam giác APQ luôn nằm trên một đường cố định.
Câu IV (1,0 điểm) (
 2  x) 1 x  y y 1  0
1. Giải hệ phương trình: 
 x  2  y 1  3
2. Cho a,b  0 thỏa mãn a a  
1  bb   1  ab . 3 3
a  b  2023a  b  4
Tìm giá trị nhỏ nhất của biểu thức: F  ab
-------- HẾT --------
Họ và tên thí sinh:........................................... Số báo danh: ......................... Phòng thi: .....
Giám thị 1:.......................................................Giám thị 2:..................................................... Trang 0
SỞ GD&ĐT HÒA BÌNH KỲ THI TUYỂN SINH VÀO LỚP 10 TRUNG HỌC PHỔ THÔNG
NĂM HỌC 2023 – 2024
HƯỚNG DẪN CHẤM MÔN TOÁN ĐỀ CHÍNH THỨC
(Dành cho thí sinh dự thi vào lớp chuyên Toán) THUC
Hướng dẫn chấm gồm có 03 trang
Câu I (3,0 điểm) Phần Nội dung Điểm 2
A  ( 5 1) ( 5 1) 0,5 1
A  ( 5 1)( 5 1)  4 0,5 x  x  1 Theo ĐL Viét, ta có: 1 2  0,5 x x  3 1 2 2 2 2 2 2 x x x  x
(x  x )  2x x 1  2.(3) 7 1 2 1 2 1 2 1 2 B       0,5 x x x x x x 3 3 2 1 1 2 1 2 ĐK: m  2  3 3 3  ( A ;0)  OA   0,5 m  2 m  2 m  2
 B(0;3)  OB  3 3 3
Ta có tam giác AOB cân tại O nên OA  OB   3 0,25 m  2  3  3  
m  1 (TM ) m 2     0,25 3 
m   3 (TM )  3 m  2
Câu II (3,0 điểm) Phần Nội dung Điểm 2 2 2
(4x  7x  4)(3x  4x  3)  3x (1) 0,25
Ta thấy x = 0 không phải là nghiệm của phương trình (1).
Xét x khác 0, chia cả 2 vế của (1) cho 2
x ta được phương trình. 4 3  1   1  0,25
(4x  7  )(3x  4  )  3  4(x  )  7 . 3(x  )  4  3     x x  x   x  Đặ 1 t x 
 t . Ta được phương trình: x t  1 0,25 1 2 (4t 7)(3t 4) 3 12t 37t 25 0          25  t   12 1 * Với t = 1 2
 x   1  x  x 1  0 (Phương trình vô nghiệm). x  4 x  0,25 25 1 25  * Với t = 2 3  x  
12x  25x 12  0   . KL.... 12 x 12 3 x   4
x  my  3m  3
x  my  3m  3    0,25 2 2
mx  y  2m  2 (
 m 1)x  2m  5m  3
Để hệ phương trình có nghiệm duy nhất thì 2
m 1  0  m  1  2m  3 5 x   2   m 1 m 1 2
Suy ra hệ phương trình có nghiệm duy nhất là  0,25 5 y  3  m 1
Vì m nguyên để hệ phương trình có nghiệm duy nhất là các số nguyên thì 0,25
m + 1 phải là ước của 5  m 11;1;5;  5
 m0;2;4;  6 (TM ) . KL... 0,25
Gọi số lần đi của Robot (theo quy luật đi rồi lại nghỉ) là x (x > 1, x *   )
Thời gian đi của Robot theo quy luật là: 0,25 120 240 360 120x 3x(x 1)    ... 
 3  6  9  ...  3x  (phút) 40 40 40 40 2  Thời gian nghỉ của x(x 1)
Robot là: 1  2  3  ....  x 1  (phút) 0,25 2 3  
Theo bài ra ta có phương trình 3x(x 1) x(x 1) : 2 
 253  2x  x  253  0 0,25 2 2 Giải phương trình 23
tìm được: x  11 (TM ); x   (KTM ) 1 2 2 0,25
Quãng đường từ A đến B 3.11.12 là: .40  7920 (cm) 2
Câu III (3,0 điểm) Phần Nội dung Điểm 0 0 0
BEP  BCP  90  90  180  tứ giác BEPC nội tiếp. 0,5
 EPC  EBA (vì cùng bù với EBC ) a
 EDA  EBA (góc nội tiếp cùng chắn cung AE) 0,5
 EDA  APQ  Tứ giác PEDQ nội tiếp.
AMQ  APQ  APQ  ADE  AMQ  ADK 0,5 b
 AKD ” AQM (QAM chung; ADK  AMQ) 0,5 AK AD c
 AKD ” AQM  
 AK.AM  A . D AQ 0,25 AQ AM Trang 1 Ta có: 0
ADB ” ACQ (A chung; ADB  ACQ  90 ) AD AB    0,25 A . B AC  A .
D AQ  AK.AM  A . B AC AC AQ A . B AC
Ta có AK.AM  A . B AC  AM 
(không đổi)  M cố định. 0,25 AK d
Gọi I là tâm đường tròn ngoại tiếp tam giác APQ thì ta có IA  IM nên 0,25
I nằm trên đường trung trực của AM cố định.
Câu IV (1,0 điểm) Phần Nội dung Điểm
ĐKXĐ: 2  x  1; y  1
(1)  (1 x) 1 x  ( y 1) y 1  1 x  y 1  0
Đặt 1 x  u (u  0); y 1  t (t  0) ta được phương trình: 0,25 u   t  0 3 3
u  t  u  t  0 2 2
 (u  t)(u  ut  t 1)  0   2 2 u
  ut  t 1  0 1
 u t  0 1 x  y 1 x  2  y .
Từ (2) suy ra 4  y  y 1  3 (ĐKXĐ: 1  y  4 ) 2 2
 5  2 (4  y)(y 1)  9  4  3y  y  2  3y  y  0
y  0 (KTM ) 0,25
 y 3 (TM) Vậy hệ có nghiệm ( ; x y)  (1;3).
Từ giả thiết a a    bb   2 2 1
1  ab  a  b  a  b  ab 2 2
 a  b  ab  a  b
Theo bất đẳng thức AM-GM, ta có: 2 2
a  b  2ab  ab  a  b  2ab  a  b  ab (1) 0,25
Lại có: ab  a  b    2 a     2 8 4
b  4  4a  4b  4a  b
 ab  8  3a  b  3ab (do ( ) 1 )  ab  4 . Đặ 2 4 t t 
ab  0  t  2   1  1. 2 t t 2
Áp dụng bất đẳng thức AM-GM, ta có: 2 2 2 2 a b  1 1  4 a b 1 4 F    2023     2 .  2023.2  b a  a b  ab b a ab ab 1 4  2t  4046.  0,25 2 t t 8 2 4 F  2t   2019   . 2 t t t 8 8
Theo bất đẳng thức AM-GM, ta có 2t   2 2t.  8 t t
 F  8 20191 2028. Vậy min F  2028 , đạt khi a  b  2 . Trang 2
* Chú ý: Các lời giải đúng khác đều được xem xét cho điểm tương ứng.
– – – – – HẾT – – – – – Trang 3