Đề thi tuyển sinh vào lớp 10 THPT năm học 2023-2024 môn toán Sở GD tỉnh Hà Giang (có đáp án và lời giải chi tiết

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT TỈNH HÀ GIANG NĂM HỌC 2023 - 2024
ĐỀ THI MÔN: TOÁN HỌC (dành cho tất cả các thí sinh)
Thời gian làm bài: 120 phút ĐỀ CHÍNH THỨC Ngày thi: 08/06/2023 Câu 1 (2,5 điểm):
a) Tính giá trị biểu thức A  36  9  25.
2x  y  5
b) Giải hệ phương trình  . x  y 1 c) Rút gọn biểu thức 1 1 4 C   
với x  0 và x  4. x  2 x  2 x  4 Câu 2 (2,0 điểm):
a) Cho hàm số y  2m  6 x  m . Tìm m để thị đồ hàm số đã cho đi qua điểm A1;6. b) Giải phương trình 2
x  5x  6  0.
Câu 3 (1,5 điểm): Một xe ô tô và một xe máy cùng khởi hành từ thành phố Hà Giang đến trung
tâm huyện Bắc Quang dài 60 .
km Biết vận tốc xe ô tô lớn hơn vận tốc xe máy là 10km / h nên
xe ô tô đến trung tâm huyện Bắc Quang sớm hơn xe máy 18 phút. Tính vận tốc của mỗi xe.
Câu 4 (1,0 điểm): Bố bạn An dùng một chiếc thang dài 3m để trèo lên sửa bóng điện trong
nhà. Khi đó An đo được khoảng cách từ vị trí đặt chân thang đến chân tường là 1,5 . m Theo kinh
nghiệm thực tế, thang phải tạo với sàn nhà một góc có số đo từ 0 50 đến 0
70 mới đảm bảo an
toàn. Vậy bố bạn An đã sử dụng thang đảm bảo an toàn chưa? (giả sử tường xây theo phương
thẳng đứng, sàn nhà phẳng theo phương ngang). (Hình vẽ minh họa)
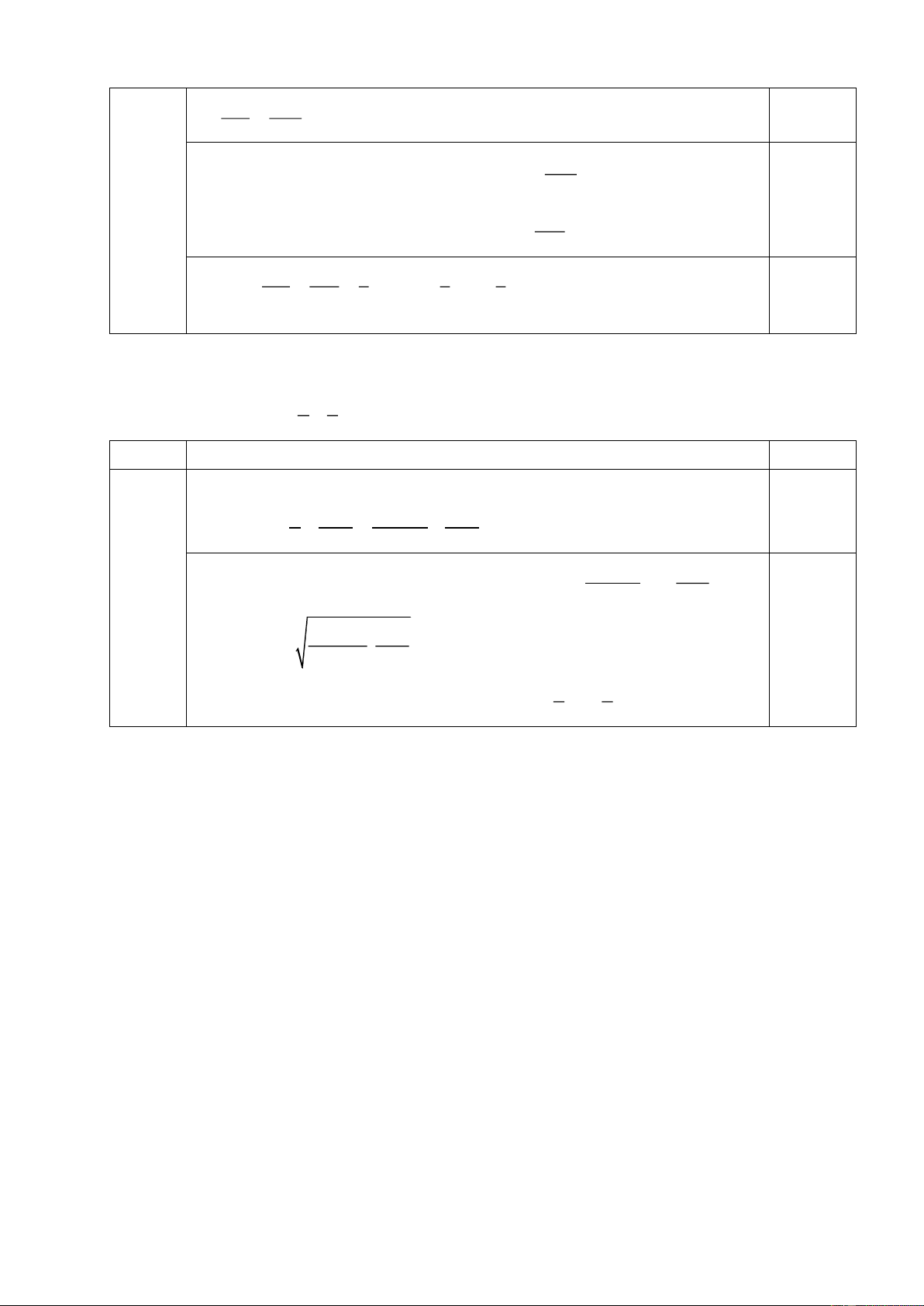
Câu 5 (2,5 điểm): Cho nửa đường tròn tâm O đường kính .
AB Bán kính OC vuông góc với .
AB Điểm E thuộc đoạn .
OC Tia AE cắt nửa đường tròn O tại M.
a) Chứng minh tứ giác OEMB là tứ giác nội tiếp.
b) Gọi K là giao điểm của BM và OC, chứng minh BM.BK  B . A B .
O Tìm vị trí của
điểm E để MA  3MB khi E di chuyển trên đoạn . OC
Câu 6 (0,5 điểm): Cho hai số dương a và b thỏa mãn điều kiện a  b 1. Tìm giá trị nhỏ 9 1
nhất của biểu thức P   . a b
----------- HẾT ----------
(Thí sinh không được sử dụng tài liệu; Cán bộ coi thi không giải thích gì thêm).
Họ và tên thí sinh: ………….……………Số báo danh: …………….……………….
Họ tên CBCT 1: ……………………..........Họ tên CBCT 2:……………………….... Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT TỈNH HÀ GIANG NĂM HỌC 2023 - 2024
HDC ĐỀ CHÍNH THỨC
Hướng dẫn chấm thi môn Toán dành cho tất cả các thí sinh
(Bản hướng dẫn chấm gồm 04 trang)
Một số lưu ý khi chấm
1. Nếu thí sinh không làm bài theo cách nêu trong đáp án mà vẫn đúng và biện luận
chặt chẽ (cho dù dùng kiến thức nâng cao hoặc vượt chương trình) thì vẫn cho đủ điểm như
hướng dẫn quy định (đối với từng phần)
2. Việc chi tiết hóa thang điểm (nếu có) so với thang điểm hướng dẫn chấm phải bảo
đảm không sai lệch với hướng dẫn chấm và được thống nhất thực hiện trong hội đồng chấm thi.
3. Điểm bài thi là tổng điểm các câu thành phần và không được làm tròn; đề thi thang điểm 10. Câu 1 (2,5 điểm):
a) Tính giá trị biểu thức A  36  9  25.
2x  y  5
b) Giải hệ phương trình  . x  y 1 c) Rút gọn biểu thức 1 1 4 C   
với x  0 và x  4 . x  2 x  2 x  4 Câu Đáp án Điểm
Câu 1a Ta có A  36  9  25  635  4. (0,5 đ) 0,5
2x  y  5 3  x  6 Ta có:    0,5 x  y  1 x  y  1 x  2 Câu 1b   0,25    (1,0 đ) 2 y 1 x  2  
. Vậy hệ đã cho có nghiệm là  ; x y  2;  1 . 0,25  y  1
Với x  0 và x  4 ta có: 1 1 4
x  2  x  2  4 C     0,25 x  2 x  2 x  4
 x 2 x 2 Câu 1c 2 x  4 (1,0 đ)   0,25
x  2 x  2 2 x  2   0,25
x  2 x  2 Trang 2 2  . 0,25 x  2 Câu 2 (2,0 điểm):
a) Cho hàm số y  2m  6 x  m. Tìm m để thị đồ hàm số đã cho đi qua điểm A1;6. b) Giải phương trình 2
x  5x  6  0. Câu Đáp án Điểm Câu
Đồ thị hàm số đã cho đi qua điểm A1;6 nên ta có: 2m  6.1 m  6 0,5 2a
 3m 12  m  4. (1,0 đ) 0,5
Vậy m  4 thỏa mãn bài toán. Câu Ta có 2   5  4.1.6 1. 0,5 2b
Phương trình đã cho có hai nghiệm phân biệt là: 0,5 (1,0 đ) x  2  và x  3.  1 2
Câu 3 (1,5 điểm): Một xe ô tô và một xe máy cùng khởi hành từ thành phố Hà Giang đến
trung tâm huyện Bắc Quang dài 60 .
km Biết vận tốc xe ô tô lớn hơn vận tốc xe máy là
10km / h nên xe ô tô đến trung tâm huyện Bắc Quang sớm hơn xe máy 18 phút. Tính vận tốc của mỗi xe. Câu Đáp án Điểm
Gọi vận tốc của xe máy là x km / h,x  0. 0,25
Suy ra vận tốc của ô tô là x 10 km / h. 0,25
Thời gian xe máy đi là 60 (h). x 0,25
Câu 3 Thời gian ô tô đi là 60 (h). (1,5 đ) x 10
Theo bài ra ta có phương trình 60 60 3   . 0,25 x x 10 10
Giải phương trình ta được x  40, x  50  (loại). 0,25
Vậy vận tốc của xe máy là 40 km / h, vận tốc của ô tô là 50 km / h. 0,25
Câu 4 (1,0 điểm): Bố bạn An dùng một chiếc thang dài 3m để trèo lên sửa bóng điện trong
nhà. Khi đó An đo được khoảng cách từ vị trí đặt chân thang đến chân tường là 1,5 . m Theo
kinh nghiệm thực tế, thang phải tạo với sàn nhà một góc có số đo từ 0 50 đến 0 70 mới đảm
bảo an toàn. Vậy bố bạn An đã sử dụng thang đảm bảo an toàn chưa? (giả sử tường xây theo
phương thẳng đứng, sàn nhà phẳng theo phương ngang). (Hình vẽ minh họa) Trang 3 Câu Đáp án Điểm
Hình minh họa cho bài toán C 0,25 3m Câu 4 (1,0 đ) A B 1,5m Xét ABC  vuông tại , A ta có: AB 1,5 1 0,25 cos B    . BC 3 2 Suy ra µ 0
B  60 (Thang tạo với sàn nhà một góc 0 60 ). 0,25
Vậy Bố An đã sử dụng thang đảm bảo an toàn. 0,25
Câu 5 (2,5 điểm): Cho nửa đường tròn tâm O đường kính .
AB Bán kính OC vuông góc với .
AB Điểm E thuộc đoạn .
OC Tia AE cắt nửa đường tròn O tại M.
a) Chứng minh tứ giác OEMB là tứ giác nội tiếp.
b) Gọi K là giao điểm của BM và OC, chứng minh BM.BK  B . A B .
O Tìm vị trí của
điểm E để MA  3MB khi E di chuyển trên đoạn . OC Câu Đáp án Điểm Vẽ hình đúng 0,25 Câu 5a (1,0 đ)
Xét tứ giác OEMB có · 0
EOB  90 (giả thiết). 0,25 Lại có · 0
BME  90 (Góc nội tiếp chắn nửa đường tròn). 0,25 Từ đó · · 0
EOB  BME  180 . Vậy tứ giác OEMB là tứ giác nội tiếp. 0,25 · Câu Xét A  MB và K
 OB có ABK là góc chung. 0,25 5b · · 0
AMB  KOB  90 . 0,25
(1,5 đ)  AMB đồng dạng với K  OB 0,25 Trang 4  AB BM 
 BM.BK  A . B B . O 0,25 BK BO Trong A
 MB vuông tại M có · MB tan MAB  . MA 0,25 Trong A
 OE vuông tại O có · EO tan EAO  . OA EO MB 1 1 1 Suy ra 
  OE  OA  OC. Vậy điểm E thuộc đoạn OA MA 3 3 3 0,25
OC thỏa mãn OC  3O . E
Câu 6 (0,5 điểm): Cho hai số dương a và b thỏa mãn điều kiện a  b  1. Tìm giá trị nhỏ nhất của biểu thức 9 1 P   . a b Câu Đáp án Điểm
Ta có a  b 1 b 1 . a  0,25 Khi đó 9 1 9(1 a) a P     10. a 1 a a 1 a  a a
Câu 6 Áp dụng bất đẳng thức Cô – si cho hai số dương 9(1 ) và a 1 a (0,5 đ) 91 a ta được a P  2 . 10 16. 0,25 a 1 a
Giá trị nhỏ nhất của P là 16 đạt được khi 3 1 a  , b  . 4 4
----------- HẾT ---------- Trang 5