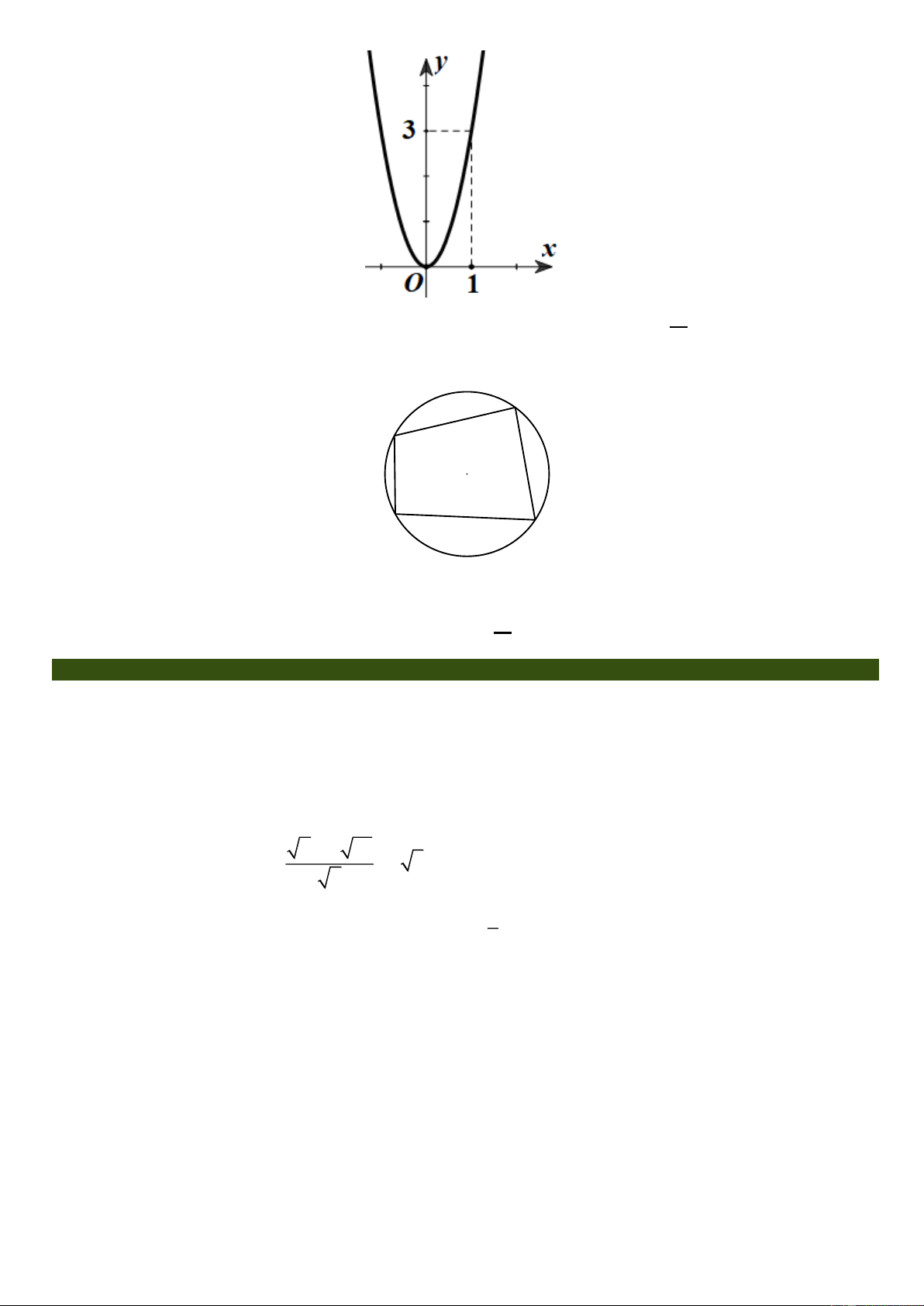




Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 THPT
THÀNH PHỐ CẦN THƠ NĂM HỌC 2023 - 2024
Khóa ngày 05 tháng 6 năm 2023 ĐỀ CHÍNH THỨC MÔN: TOÁN
(Đề thi có 04 trang)
Thời gian làm bài: 120 phút, không kể thời gian phát đề Mã đề thi
Họ và tên thí sinh:................................................................ SBD:..................... 906
A. PHẦN TRẮC NGHIỆM (4,0 điểm; gồm 20 câu, từ câu 1 đến câu 20).
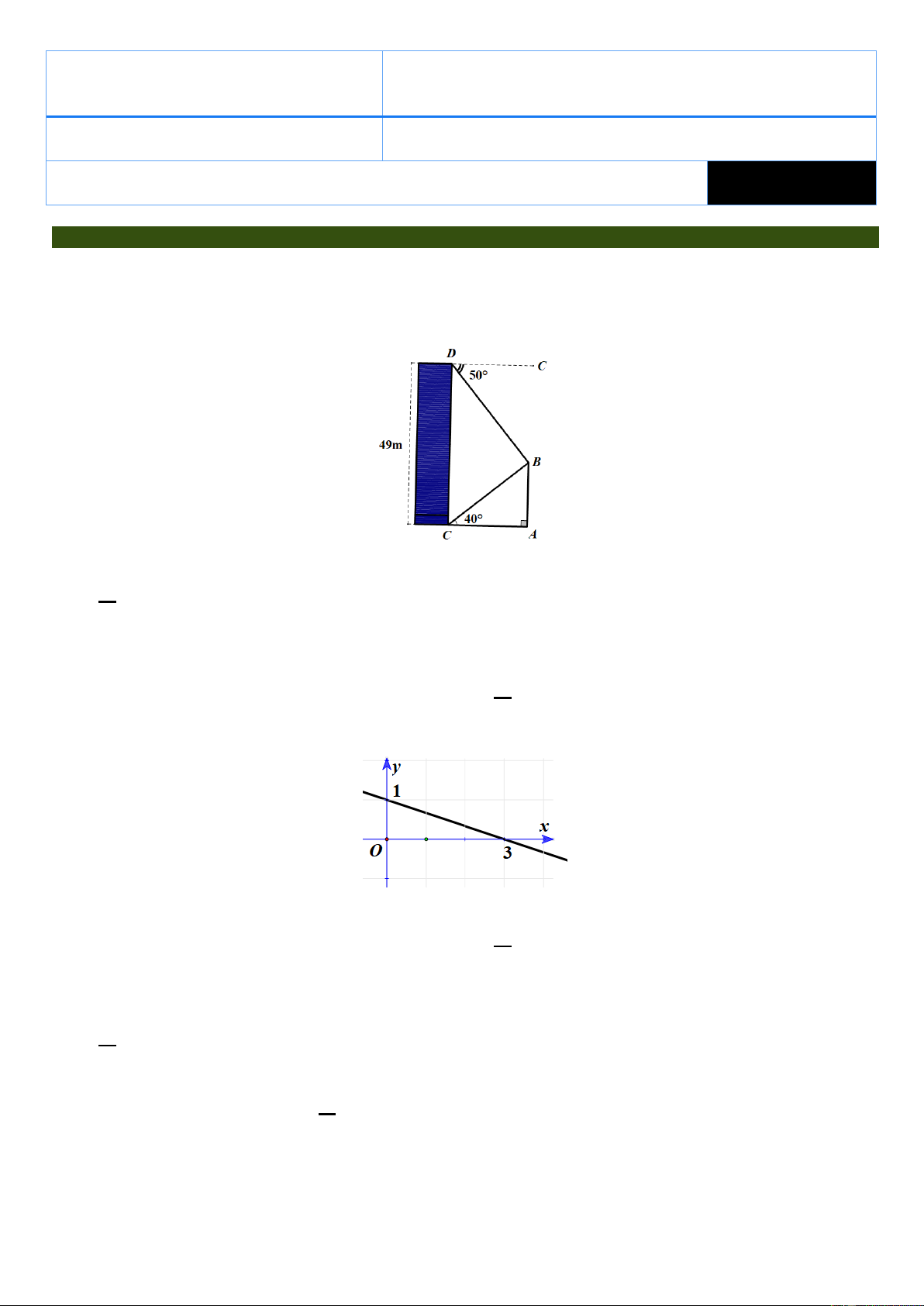
Câu 1: Từ chân C của một tòa nhà cao 49m nhìn lên một góc 40 thấy ngọn B của một cây AB và từ đỉnh D
của tòa nhà này nhìn xuống một góc
50 cũng thấy ngọn B của cây đó (minh họa hình vẽ bên dưới).
Chiều cao của cây AB (làm tròn chữ số thập phân thứ nhất) là A. 20, 2 . m B. 24,1 . m C. 28,8 . m D. 22, 2 . m
Câu 2: Cho đường tròn O có bán kính R 4cm và đường thẳng d tiếp xúc với O tại điểm M. Độ dài đoạn thẳng OM bằng A. 8 . cm B. 2 . cm C. 4 . cm D. 1 . cm
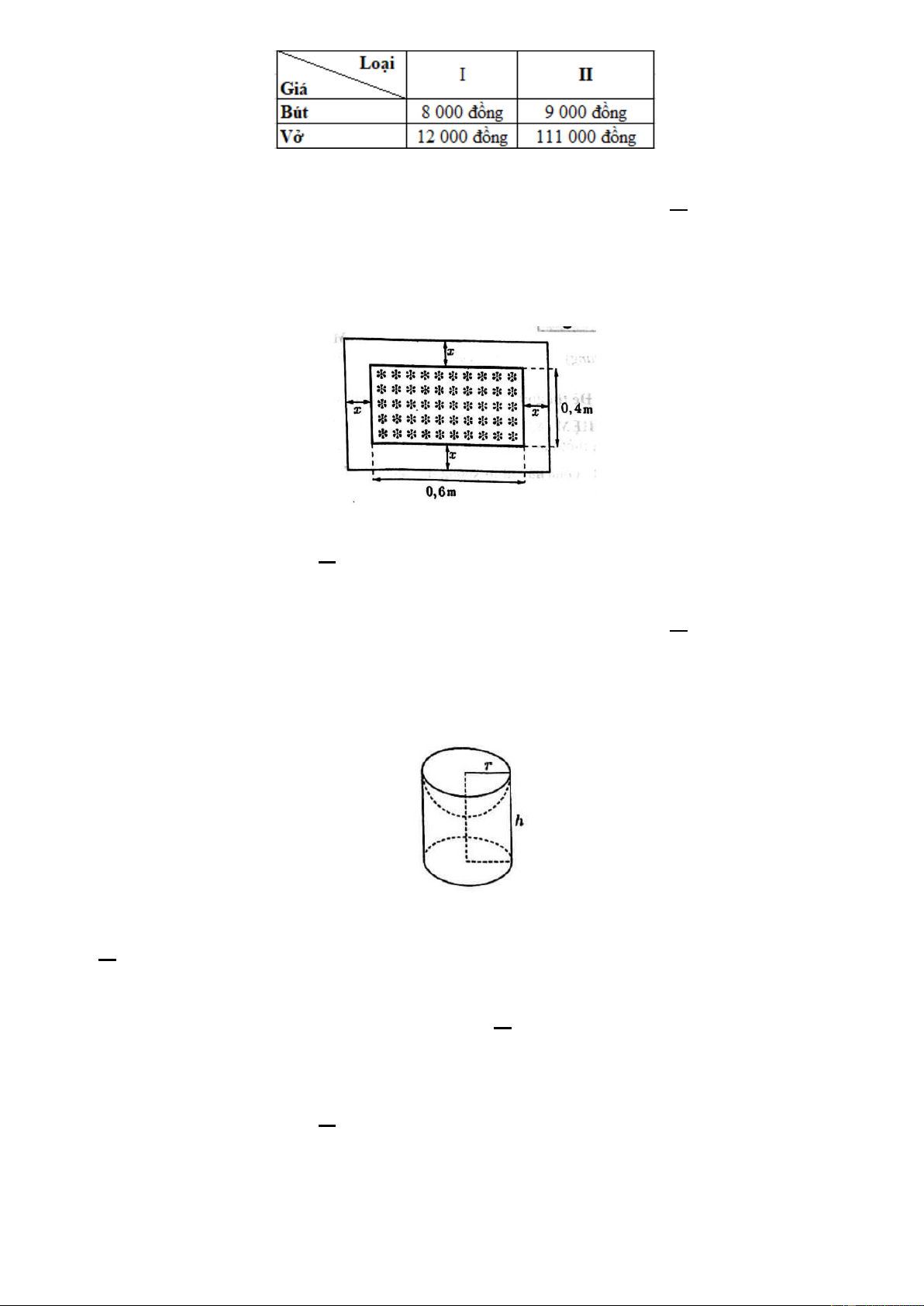
Câu 3: Cho hàm số y ax b a 0 có đồ thị là đường thẳng như hình vẽ bên dưới.
Giao điểm của đồ thị hàm số đã cho với trục hoành có tọa độ là A. 1;0 . B. 0 ;1 . C. 3;0 . D. 0;3 .
Câu 4: Cho hai số x , x thỏa mãn x x 11 và x x 30 . Khi đó x , x là các nghiệm của phương trình nào 1 2 1 2 1 2 1 2 sau đây ? A. 2
x 11x 30 0 . B. 2
x 11x 30 0 . C. 2
x 11x 30 0 . D. 2
x 11x 30 0 .
Câu 5: Gọi x , x là hai nghiệm của phương trình 2
x 5x 6 0 . Giá trị của x x bằng 1 2 1 2 A. 6 . B. 5 . C. 5 . D. 6 .
Câu 6: Hai bạn Phú và Lộc đến một nhà sách để mua bút và vở. Bạn Phú mua x cây bút loại I và y cây bút
loại II với tổng số tiền 97 000 đồng. Bạn Lộc mua x quyển vở loại I và y quyển vở loại II với tổng số tiền
123 000 đồng. Giá bán của một cây bút và một quyển vở được cho bởi bảng sau: Trang 1 Giá trị của , x y là
A. x 3, y 8 .
B. x 4, y 7 .
C. x 5, y 6 .
D. x 2, y 9 .
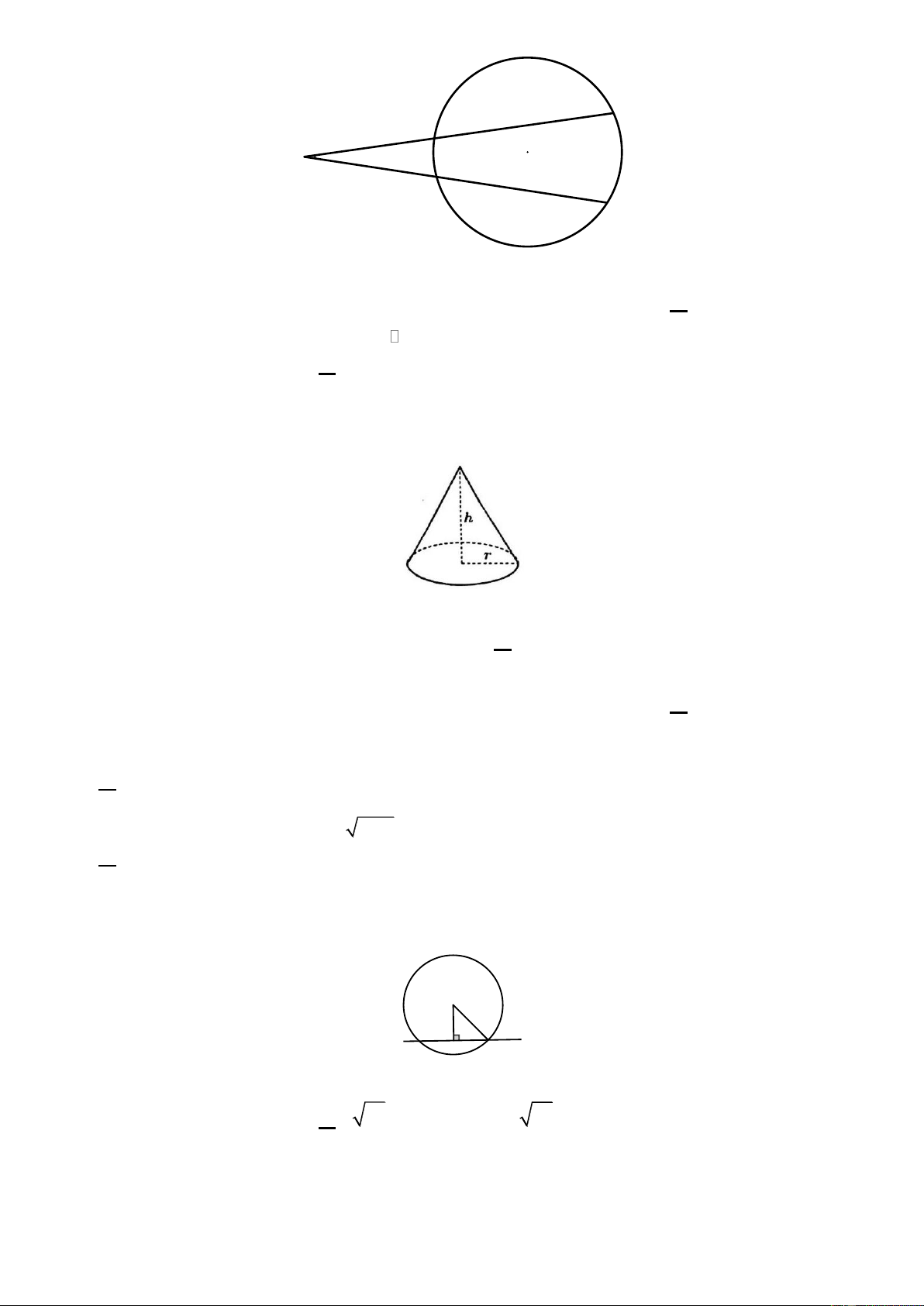
Câu 7: Bạn Kiều đặt một bức tranh hình chữ nhật có chiều rộng 0, 4m và chiều dài 0, 6m lên một khung hình
sao cho phần còn lạo của khung hình quanh bức tranh có độ rồng bằng nhau và bằng x m(minh họa hình
bên dưới). Biết chu vi của khung hình là 3, 2m .
Giá trị của x bằng A. 0,1 . B. 0,15 . C. 0, 2 . D. 0, 05 .
Câu 8: Tập nghiệm của phương trình 2
x 3x 4 0 là A. 1 . B. 4 ;1 . C. 4 . D. 1 ; 4 .
Câu 9: Bác Bảy có một khối gỗ hình trụ với bán kính đường tròn đáy r 6cm và chiều cao h 12cm . Bác
Bảy khoét khối gỗ đó một nửa hình cầu có bán kính bằng bán kính đáy của khối gỗ (minh họa như hình bên dưới).
Thể tích khối gỗ còn lại là A. 3 288 cm . B. 3 144 cm . C. 3 432 cm . D. 3 216 cm .
Câu 10: Cho hàm số y x b có đồ thị đi qua điểm A1; 2
. Giá trị của b bằng A. 1. B. 1. C. 3 . D. 3 .
x 3y 23
Câu 11: Nghiệm của hệ phương trình là
2x y 4 A. 6 ; 5 . B. 5;6 . C. 6;5 . D. 5 ; 6 .
Câu 12: Cho đường tròn O có hai dây MN và PQ. Hai đường thẳng MN và PQ cắt nhau tại điểm I (minh
họa hình vẽ bên dưới). Biết
sđ MmP 35 , sđ NnQ 75 . Trang 2 N M I m O n P Q
Số đo của NIQ bằng A. 10 . B. 55 . C. 40 . D. 20 .
Câu 13: Hàm số nào sau đây đồng biến trên ? A. 2 y 3 x .
B. y 3x 2 . C. y 3 x 2 . D. 2 y 3x .
Câu 14: Cho hình nón có bán kính đường tròn đáy r 9cm và chiều cao h 12cm (minh họa như hình bên dưới).
Diện tích xung quanh hình nón đã cho bằng A. 2 108 cm . B. 2 216 cm . C. 2 135 cm . D. 2 270 cm .
Câu 15: Đường thẳng nào sau đây song song với đường thẳng y 7x 8 ?
A. y 8x 7 .
B. y 7x 8 .
C. y 8x 7 .
D. y 7x 8 .
Câu 16: Điểm nào sau đây thuộc đồ thị của hàm số 2 y 4 x ? A. (1;- 4). B. (1; 4). C. (4; ) 1 . D. (- 4;- ) 1 .
Câu 17: Điều kiện của x để biểu thức x 5 có nghĩa là
A. x ³ - 5 .
B. x ³ 5 .
C. x £ - 5 .
D. x £ 5 .
Câu 18: Cho đường tròn (O) có bán kính R 7cm và đường thẳng d cắt O tại hai điểm phân biệt A, B .
Biết khoảng cách từ điểm O đến đường thẳng d bằng 6cm (minh họa như hình bên dưới). O d A B
Độ dài dây AB bằng
A. 13cm .
B. 2 13cm .
C. 13cm . D. 26cm .
Câu 19: Hàm số nào sau đây có đồ thị như hình vẽ bên dưới Trang 3
A. y = - x + 4 . B. 2
y = - 3x .
C. y = x + 2 . D. 2 y = 3x .
Câu 20: Cho tứ giác EFGH nội tiếp đường tròn O (minh họa như hình bên dưới). F E O H G
Số đo góc E G bằng
A. 270o .
B. 360o .
C. 180o . D. 90o .
B. PHẦN TỰ LUẬN (6,0 điểm ; gồm 4 câu, từ câu 1 đến câu 4)
Câu 1. (1,0 điểm) Giải phương trình và hệ phương trình sau:
2x y 7 a/ 2
3x 5x 12 0. b/
x 2y 6 Câu 2.(1,0 điểm)
a/ Rút gọn biểu thức 2 6 2 18 Q 3 1 . 6 3
b/ Trên mặt phẳng tọa độ Oxy , vẽ đồ thị hàm số 2 y x 2 . Câu 3. (1,5 điểm)
a/ Một phòng giáo dục và đào tạo phát động phong trào “Học sinh quyên góp sách giáo khoa lớp 9”
nhằm giúp học sinh lớp 9 có hoàn cảnh khó khăn. Hưởng ứng phong trào trên, tổng số học sinh tham gia của
Trường Trung học cơ sở A và Trường Trung học cơ sở B là 322. Mỗi học sinh của Trường Trung học cơ sở
A quyên góp 6 quyển sách, mỗi học sinh của Trường Trung học cơ sở B quyên góp 5 quyển sách. Tổng số
sách quyên góp của Trường Trung học cơ sở A nhiều hơn tổng số sách quyên góp của Trường Trung học cơ
sở B là 172quyển. Hỏi mỗi trường đã quyên góp được bao nhiêu quyển sách giáo khoa? Trang 4
b/ Tìm tất cả giá trị của tham sốm sao cho phương trình 2 2
x (2m 1)x m 1 0 có hai nghiệm phân biệt 2 2
x ; x thỏa mãn x 1 x 1 13 1 2 1 2
Câu 4. (2,5 điểm) Cho tam giác ABC AB AC có ba góc nhọn, nội tiếp đường tròn tâm O. Tiếp
tuyến tại A của đường tròn O cắt đường thẳng BC tại K. Từ O kẻ OD vuông góc với BC tại D, tia OD cắt
đường tròn O tại E.
a/ Chứng minh tứ giác KDOA nội tiếp.
b/ Đường thẳng AE cắt BC tại N. Chứng minh tam giác KNA cân và 2 KN . KB KC.
c/ Kẻ tiếp tuyến KM của đường tròn O (M là tiếp tuyến). Chứng minh tia MN và tia ED cắt nhau tại
một điểm thuộc đường tròn O .
------------------ HẾT ------------------
(Học sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.) Trang 5
ĐÁP ÁN TRẮC NGHIỆM 1A 2C 3C 4A 5B 6D 7B 8D 9A 10C 11B 12D 13B 14C 15D 16A 17A 18B 19D 20C HD GIẢI TỰ LUẬN
Câu 1. (1,0 điểm) Giải phương trình và hệ phương trình sau: a/ 2
3x 5x 12 0. Giải. 2 5 4.3. 1 2 169 0
Nên phương trình có hai nghiệm phân biệt 5 169 4 5 169 x , x 3 1 2 2.3 3 2.3 Vậy 4 S ; 1 3
2x y 7 b/
x 2y 6 Giải.
4x 2y 14 5 x 20 x 4 x 4 HPT .
x 2y 6
x 2y 6
x 2y 6 y 1
Vậy hệ có nghiệm duy nhất ; x y 4; 1 . Câu 2.(1,0 điểm)
a/ Rút gọn biểu thức 2 6 2 18 Q 3 1 . 6 Giải. 6 1 2 3 Q
4 2 3 1 2 3 4 2 3 3 6 Vậy Q 3 . 3
b/ Trên mặt phẳng tọa độ Oxy , vẽ đồ thị hàm số 2 y x 2 . Bảng giá trị Đồ thị Trang 6 Câu 3. (1,5 điểm)
a/ Một phòng giáo dục và đào tạo phát động phong trào “Học sinh quyên góp sách giáo khoa lớp 9”
nhằm giúp học sinh lớp 9 có hoàn cảnh khó khăn. Hưởng ứng phong trào trên, tổng số học sinh tham
gia của Trường Trung học cơ sở A và Trường Trung học cơ sở B là 322. Mỗi học sinh của Trường
Trung học cơ sở A quyên góp 6 quyển sách, mỗi học sinh của Trường Trung học cơ sở B quyên góp 5
quyển sách. Tổng số sách quyên góp của Trường Trung học cơ sở A nhiều hơn tổng số sách quyên góp
của Trường Trung học cơ sở B là 172quyển. Hỏi mỗi trường đã quyên góp được bao nhiêu quyển sách giáo khoa? Giải. Gọi ,
x y lần lượt là số học sinh của Trường A và Trường B (điều kiện x, y )
x y 322
Theo đề bài ta có hệ phương trình
6x 5y 172
Giải hệ được x 162, y 160 .
Vậy Trường A đã quyên góp được 162.6 972quyển; Trường B quyên góp được 160.5 800 quyển.
b/ Tìm tất cả giá trị của tham sốm sao cho phương trình 2 2
x (2m 1)x m 1 0 có hai nghiệm phân biệt 2 2
x ; x thỏa mãn x 1 x 1 13 1 2 1 2 Giải. 2 3
Ta có: 2m 1 4. 2 m
1 4m 3 0 m . 4
Khi đó phương trình có 2 nghiệm phân biệt x , x . Theo vi-et, có : 1 2 2
x x 2m 1; x x m 1 1 2 1 2 2 2 2 Xét:
x 1 x 1 13 x x 2x x 2 x x 11 0 1 2 1 2 1 2 1 2
m 1 N 2
2m 8m 10 0 . m 5 L
Vậy m 1. Trang 7
Câu 4. (2,5 điểm) Cho tam giác ABC AB AC có ba góc nhọn, nội tiếp đường tròn tâm O. Tiếp tuyến tại
A của đường tròn O cắt đường thẳng BC tại K. Từ O kẻ OD vuông góc với BC tại D, tia OD cắt
đường tròn O tại E.
a/ Chứng minh tứ giác KDOA nội tiếp.
b/ Đường thẳng AE cắt BC tại N. Chứng minh tam giác KNA cân và 2 KN . KB KC.
c/ Kẻ tiếp tuyến KM của đường tròn O (M là tiếp tuyến). Chứng minh tia MN và tia ED cắt nhau tại
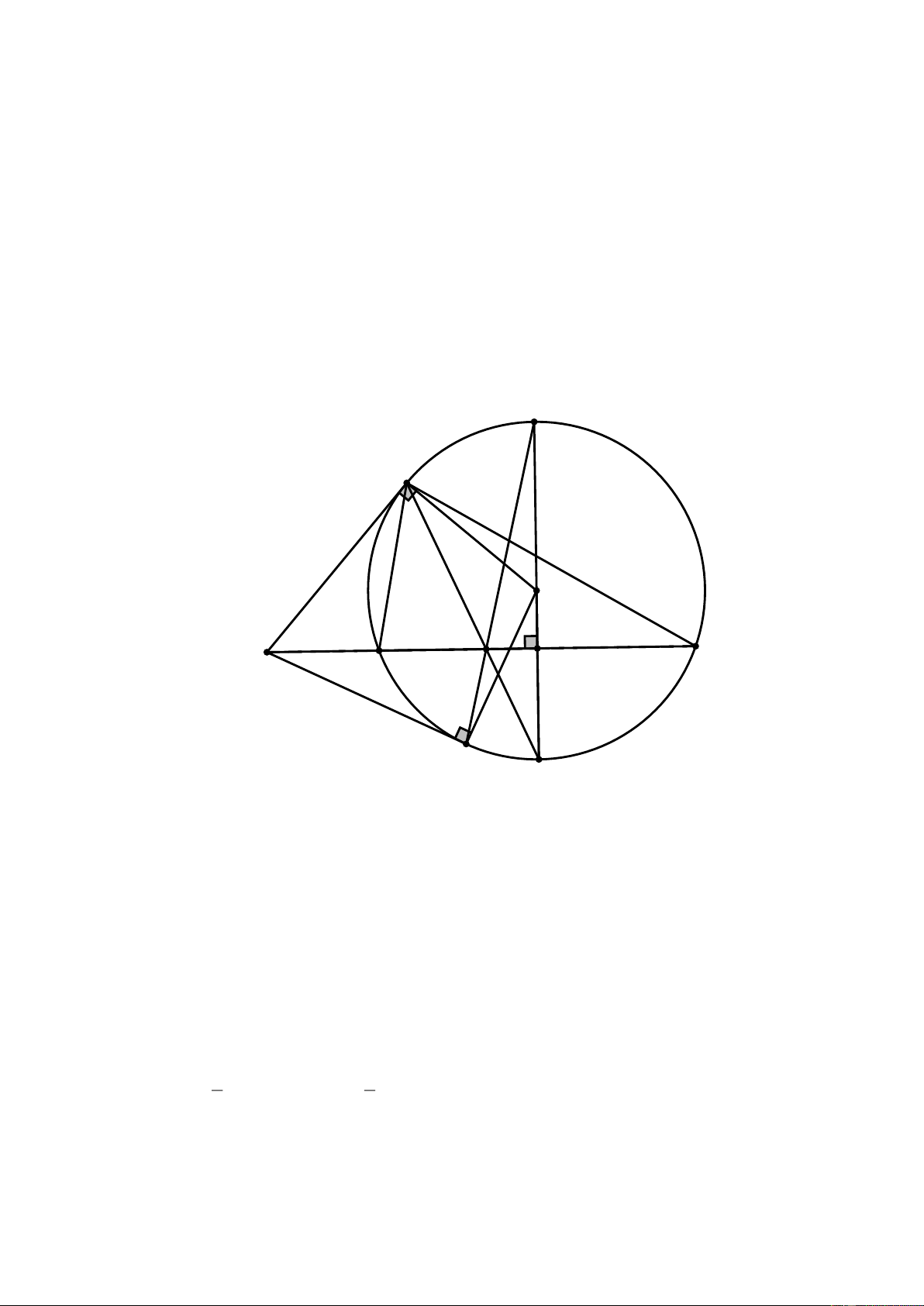
một điểm thuộc đường tròn O . Giải. P A O C N D K B M E
a) Xét tứ giác KDOA có :
KAO 90 (Ka là tiếp tuyến của đường tròn O ).
KDO 90 OD BC .
KAO KDO 180
Vậy tứ giác KDOA nội tiếp.
b) Chứng minh: KNA cân.
OD là đường trung trực của BC nên E là điểm chính giữa cung BC hay sđ CE sđ BE . 1 1 Ta có: ANK
sđABsđCE sđAE KAE KAN 2 2 K AN cân tại K. Chứng minh: 2 KN K . B KC .
Xét hai tam giác KA B, KC A có: Trang 8
K chung và KAB KCA (cùng chắn cung AB) KA B ~ KC
A (g g) KA KC 2 KA K . B KC KB KA Mà KNA
cân tại K, nên KA KN Vậy 2 KN . KB KC.
c) Gọi P là giao điểm của MN và ED . Ta cần chứng minh: P O .
Có: KA KM ( tính chất hai tiếp tuyến cắt nhau)
Mà KA KN (tam giác KAN cân tại K)
Nên KM KN KMN KNM PND
OMP 90 KMN 90 PND DPN O
NP cân tại O OP OM , mà OM là bán kính đường tròn O .
Do đó P thuộc O . Trang 9




