Đề thi tuyển sinh vào lớp 10 Trường THPT Chuyên Hà Tĩnh năm 2023-2024 môn toán (có đáp án và lời giải chi tiết)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 HÀ TĨNH
TRƯỜNG THPT CHUYÊN HÀ TĨNH
NĂM HỌC 2023 – 2024
ĐỀ THI CH ÍNH THỨC Môn: TOÁN
Thời gian làm bài: 150 phút, không kể thời gian phát đề
Câu 1. (2,0 điểm) a) Tìm các số nguyên , x y thỏa mãn 2 2
4x  5y  4xy  2(2x  3y)  4  0. 1 1 1 b) Cho a, ,
b c là các số thực khác không thỏa mãn    0. a b c 1 1 1 Chứng minh rằng    0. 2 2 2 a  2bc b  2ca c  2ab
Câu 2. (2,5 điểm)
(x  2)(2  y)  8 
a) Giải hệ phương trình  2 2
 11 4(x  y)  x y 1  3x . y  b) Giải phương trình 2
x  3x 11 
x  2  2x  2.
Câu 3. (1,5 điểm) 5
a) Tìm tất cả các số thực x để p  là số nguyên. x  x  2
b) Chứng minh rằng với mọi số tự nhiên n lớn hơn 1 thì 2024 2023 4 A  n  n
 n  n 1
không phải là số nguyên tố.
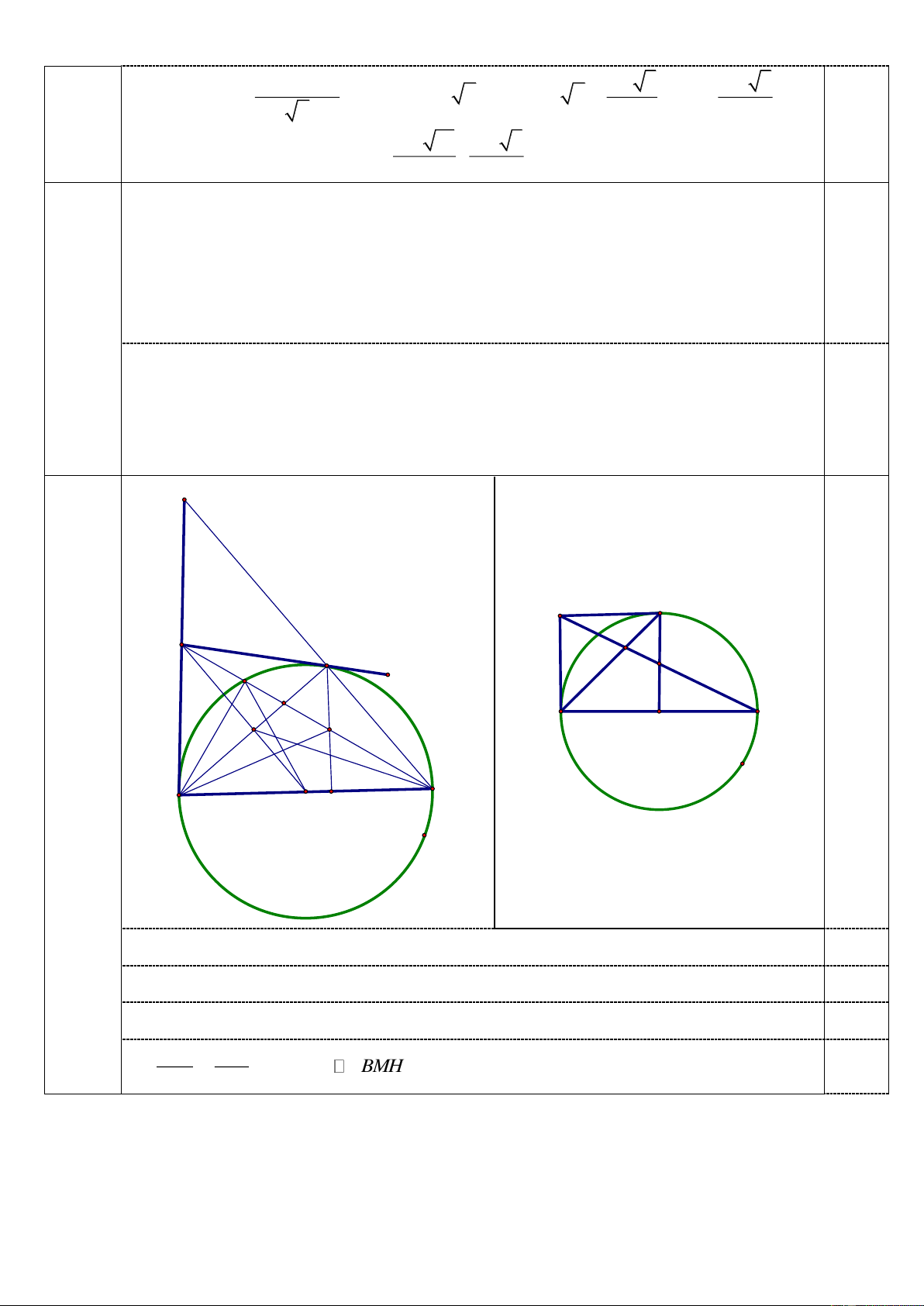
Câu 4. (2,5 điểm) Cho đường tròn O đường kính AB
cố định, C là một điểm chạy trên
đường tròn O không trùng với A và . B
O tại A và C cắt
Các tiếp tuyến của đường tròn  
nhau tại điểm M . Đường thẳng MB cắt AC tại F và cắt đường tròn O tại E
( E khác B ).
a) Gọi H là trung điểm của đoạn thẳng .
AC Chứng minh tam giác OEM đồng dạng với tam giác BHM.
b) Gọi K là hình chiếu vuông góc của C trên đường thẳng .
AB Hai đường thẳng MB FI
và CK cắt nhau tại I. Tính tỷ số
khi tổng diện tích hai tam giác IAC và IBC lớn nhất. AB 1 1 2 c) Chứng minh rằng   . BM BF BE
Câu 5. (1,0 điểm) Cho các số thực a, ,
b c thỏa mãn a  b  ;
c ab  bc  ca  0 và a  b  c  1. 1 1 1 5
Tìm giá trị nhỏ nhất của biểu thức P     . a  b b  c a  c
2 ab  bc  ca
Câu 6. (0,5 điểm) Cho , x , y z   
là các số chính phương. Chứng minh rằng  x  1  y  1  z  1
luôn viết được dưới dạng tổng của hai số chính phương. ------HẾT------
- Thí sinh không được sử dụng tài liệu.
- Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:.................................................................. Số báo danh: .................................. Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 HÀ TĨNH
TRƯỜNG THPT CHUYÊN HÀ TĨNH
NĂM HỌC 2023 – 2024
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM MÔN TOÁN
Chú ý: - Thí sinh giải theo cách khác, nếu đúng đều cho điểm tối đa.
- Điểm toàn bài không qui tròn. Câu Nội dung Điểm Câu Ta có 2 2 2 2
4x  5y  4xy  2(2x  3y)  4  0  (2x  y 1)  4( y 1) 1 0,25 1a 1,0 đ 2 2 
(2x  y 1)  4( y 1)  1   0,25 2 2
(2x  y 1)  4(y 1)  0
2x  y 1  0 x  1  TH1: 2 2
(2x  y 1)  4( y 1)  0     0,25  . y  1  0  y  1
2x  y 1  0  (vn) 2 4(y 1)  1 TH2: 2 2
(2x  y 1)  4( y 1)  1   2 2
(2x  y 1)  1 (2x  2) 1    0,25 (vn). y 1 0 y  1 
Vậy có đúng một cặp số thỏa mãn (x; y) = (-1; -1). Câu 1 1 1        1b 0 ab bc ca 0 0,25 a b c
1,0 đ Ta có : 2 2
a  2bc  a  bc  ( a  b  c ) a  (a  ) b (a  ) c . 0,5 Tương tự có : 2 2
b  2ca  (b  c)(b  a); c  2ab  (c  a)(c  ) b . 1 1 1 1 1 1      2 2 2 a  2bc b  2ca c  2ab
(a  b)(a  c)
(b  c)(b  a)
(c  a)(c  b) 0,25 1 1 1
b  c  (a  c)  a  b      0
(a  b)(a  c)
(b  c)(a  b)
(a  c)(b  c)
(a  b)(b  c)(a  c) Câu
ĐK: 11 4(x  y)  0 2a 0,25
(x  2)(2  y)  8  2 x  y  xy  4  2 x  y  4  xy 1,5 đ
Thế vào phương trình (2) ta có: 2 2 2 2 0,25
11 2(4  xy)  x y  3xy 1  0 
3  2xy  x y  3xy  1  0
   xy   2 2 3 2
1  x y  3xy  2  0 0,25 2(1 xy)   
 (1 xy)(2  xy)  0    xy 2 1   2  xy   0   0,25 3  2xy 1 3  2xy 1    2 3 xy  1 (Do
 2  xy  0, x  y  ) 0,25 3  2xy 1 2 Trang 2  1  1 y   1 y  xy  1     x y  x Ta có:      x   2
  x  y  5  1   2 5 41 2 x   5    
2x  5x  2  0 x    x   4 0,25
Vậy hệ phương trình có nghiệm là:       5  41 5   41   x y 5 41 5 41 ;   ;  và  ;  4 4   4 4   Câu 2
x  3x 11  0 2b ĐK:   x  2  x  2  0 1,0 đ 0,25 2 2
x  3x 11  x  2  2x  2 
(x 1)  5(x  2)  x  2  2(x 1) Xét x  2
 (không phải là nghiệm) 2 (x 1) 2(x 1) Xét x  2
 Chia hai vế phương trình cho x  2 ta được:  5 1  . x  2 x  2 0,25  Đặ x 1 t t  ta được phương trình: 2
t  5 1  2t x  2  1  1 t   2t 1 0 t     2 2 2
 t  5  2t 1     2    t  0,25 2 2 t   5  (2t 1) 2 3 2 3
 t  4t 4  0 t   2;  t    3 2 Khi t  ta được phương trình: 3 x 1 2 x 1  0
  2 x  2  3(x 1)   2 x  2 3
4(x  2)  9(x 1) x  1 x  1  11 4 7      x  .  2 11 4 7 0,25 9
 x  22x 1  0 x  9  9 11 4 7
Vậy phương trình có đúng 1 nghiệm x  9 a  x 1 
Chú ý: Học sinh có thể giải theo cách: Đặt  b
  x  2  0. Câu 5 5 Ta có p   3a 2 x  x  2  1  7 0,25 1,0 đ x      2  4 5 20  0  p    p  1; 2 7 7 0,25 4 5 1 13 7  13 TH1: p  1 
 1  x  x  3  0  x   x  . 0,25 x  x  2 2 2 Trang 3 5 1 3 2  3 TH2: p  2 
 2  2x  2 x 1  0  x   x  . x  x  2 2 2 0,25 7  13 2  3
Vậy có hai giá trị cần tìm là x  ; . 2 2 Câu Ta có 2024 2023 4 A  n  n
 n  n    2024 2 n  n    2023 n  n   4 2 1 n  n   1 3b 2  n  2022 n    n 2022 n     4 2
n  n     2
n  n 2022 n     4 2 1 1 1 1 n  n   0,5 đ 1   0,25      Ta có n nn
 n n n 674 2 2022 2 3 1 1     2 n  n 3
n   B   2
n  nn   2 1 .
1 n  n   1 .B chia hết cho 2 n  n 1
Lại có n  n   n  n   n  n  2 4 2 4 2 2 2 2 1 2 1 1  n   2
n  n   2
1 n  n   1 chia hết cho 2 n  n 1 0,25 Vậy 2024 2023 4 A  n  n
 n  n 1 chia hết cho 2
n  n 1 với mọi số tự nhiên n lớn
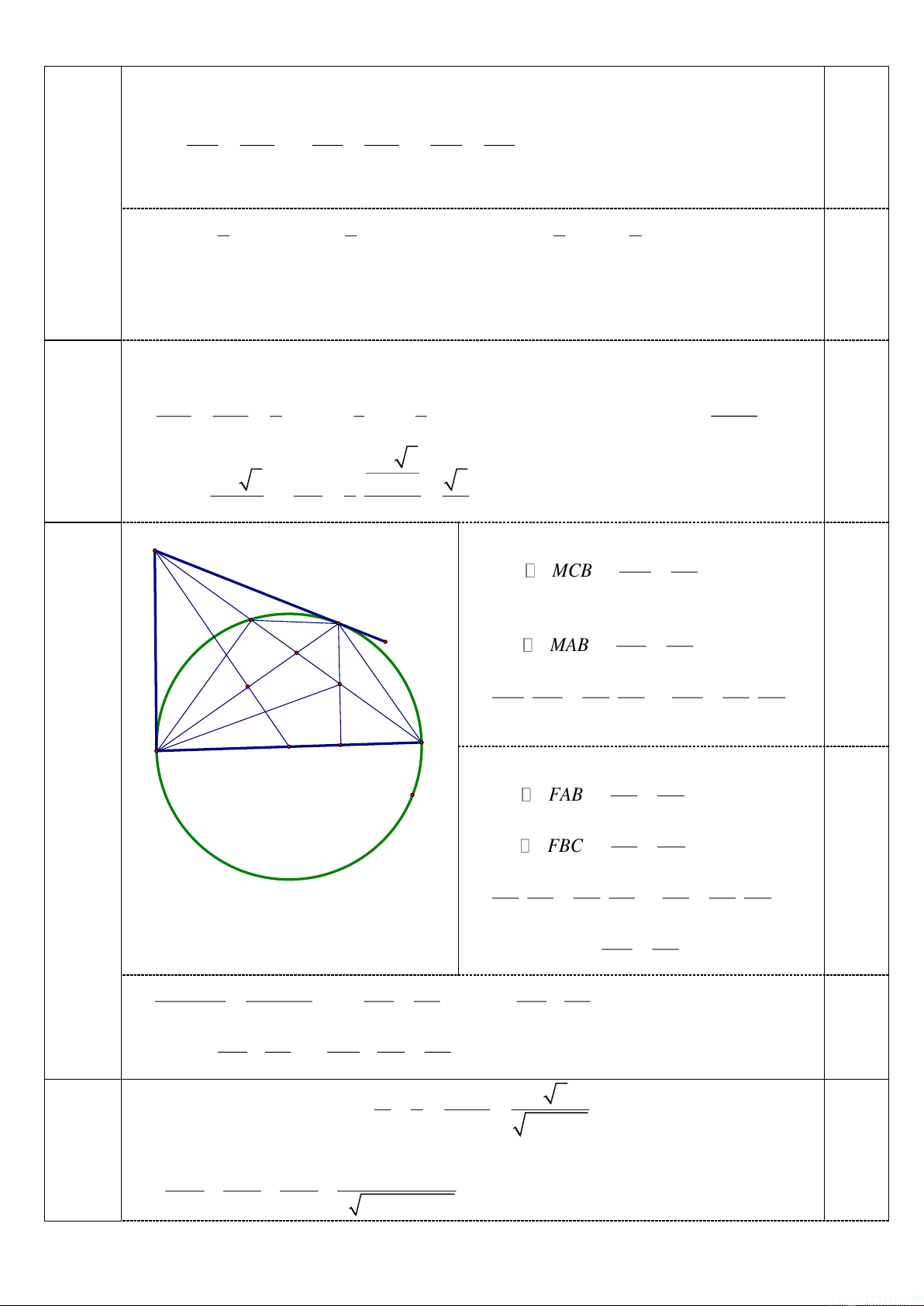
hơn 1 nên A không phải là số nguyên tố. Câu P 4a 1,0 đ M C M C F I E F A B H I O A B O K a) Ta có 2 M .
E MB  MA do M
 AB vuông tại A có đường cao AE. 0,25 Lại có 2
MH.MO  MA do M
 AO vuông tại A có đường cao AH. 0,25  M .
E MB  MH.MO 0,25 ME MO    O  ME B  MH MH MB 0,25 Trang 4 Câu
b) Ta có MA  MC, OA  OC suy ra đường thẳng MOlà trung trực đoạn thẳng AC 4b
nên MO  AC . Kéo dài BC cắt AM tại P nên MO / /PB  M trung điểm . AP 0,75 đ IC BI IK BI 0,25 Ta có  và  IC IK    IC  IK MP BM MA BM MP MA
Suy ra I trung điểm của đoạn thẳng CK . 1 1 1 1  S  S ; S  S  S  S  S  CK.AB AC  I       2 ACK BCI 2 BCK AIC BCI 2 ABC 4
Do đoạn thẳng AB không đổi nên tổng diện tích hai tam giác IAC và IBC lớn nhất. 0,25
lớn nhất khi C điểm chính giữa AB hay K trùng tâm . O
Khi đó tứ giác AOCM là hình vuông. FI IC 1 1 1 2     5AB FI  IM  BM . Lại có 2 2 2
BM  AB  MA  FM AM 2 3 6 4 0,25 AB 5 AB 5 FI 1 5 2  BM    .  . 2 AB 6 AB 12 M c) Ta có Câu 4c ME CE M  EC M  CB   0,75 đ MC CB E C MA EA 0,25 MEA  MAB    F MB AB I ME MA CE EA ME CE AE H  .  .   . (1). MC MB CB AB MB CB AB B A O K Mặt khác FE CE FEC  FAB    FA AB FA AE FAE  FBC    FB BC 0,25 FE FA CE EA FE CE AE  .  .   . (2). FA FB AB CB FB CB AB ME FE Từ (1) và (2)   MB FB MB  EB EB  FB EB EB EB EB   1  1 2   MB FB MB FB MB FB  0,25 1 1  1 1 2  2  EB       (ĐPCM).  MB FB  BM BF BE Câu 5 1 1 4 2 2 1,0 đ     
Ta sử dụng các bất đẳng thức với m 0; n 0 2 2 m n m  n m  n
Dấu bằng xảy ra khi m  n 0,25 1 1 1 5 P     a  b b  c a  c
2 ab  bc  ca Trang 5 4 1 5 5 5 P      a  c a  c
2 ab  bc  ca a  c
2 ab  bc  ca 5 5 2 2 10 2 Lại có:   5  2 2 a  c
2 ab  bc  ca
(a  c)  4(ab  bc  ca)
(a  c)  4b(a  c) 0,25 10 2 10 2  P  
do a  c 1b
(a  c)(a  c  4b)
(1 b)(1 3b) 10 6 10 6  P         5 6 3  3b 1 3 3 3 1 3 b b b 0,25 2
Giá trị nhỏ nhất của P bằng 5 6 khi
a  b  c      2  6 a b c 1 a   b   6
a  b  c  1   3     1
a  b  b  c   2  b   a  c  3    3
a  c  2 b(a  c)  ca    0,25 2  6      2   3 3 1 3 c b b a  c  2  ca   6  9 Câu 6 Vì ; x ;
y z là các số chính phương ta viết thành 2 2 2
x  a ; y  b ; z  c a; ; b c Z  0,5 đ Ta có:
a  b  c   a b a b  c    ab2 ab 2 2 2 2 2 2 2 2 2  2 1 1 1 1 1 1 c   1 0,25    
 ac  bc2 ab  2  a b2 abc c2 1     
Áp dụng các đẳng thức x  y   x  y2 2 2
 2xy và x  y  x  y2 2 2  2xy có:
Thứ 1: ac  bc2  ab  2  ab  bc  ca  2 1 1
 2ac  bcab   1 2
 ab  bc  ca     2 2 1
2 a bc  b ac  ac  bc
Thứ 2: a  b2  abc  c2  a  b  c  abc2  2a  babc  c 0,25 2
 a  b  c  abc   2 2
2 a bc  b ac  ac  bc
 ac  bc2  ab  2  a  b2  abc  c2  ab  bc  ca  2 2 1
1  (a  b  c  abc) Vậy  x   1  y   1  z  
1 là tổng của hai số chính phương. HẾT. Trang 6