Đề thi vào 10 chuyên môn Toán (chung – TN) năm 2023 – 2024 sở GD&ĐT Nam Định

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 TRƯỜNG THPT CHUYÊN NAM ĐỊNH
NĂM HỌC 2023 – 2024 ĐỀ CHÍNH THỨC
Môn thi: TOÁN (chung) – Đề: 1
Dành cho học sinh thi vào các lớp chuyên tự nhiên
Thời gian làm bài: 120 phút (không kể thời gian phát đề) Đề thi gồm 01 trang
Câu 1. (2,0 điểm)
1) Tính giá trị biểu thức P = 2024 + 2 2023 − 2025 + 2 2024 .
2) Tìm tọa độ của điểm M là giao điểm của đường thẳng y = x +1 với trục Oy.
3) Tính diện tích hình tròn ngoại tiếp tam giác vuông có cạnh huyền bằng 2 2 cm.
4) Tính thể tích của hình nón có đường sinh bằng 10 cm và bán kính đáy bằng 6 cm.
Câu 2. (1,5 điểm)  +  Cho biểu thức x 2 x 1 1 P =  + − ⋅ 
(với x ≥ 0 và x ≠ 1). x x 1 x x 1 x 1 − + + − x −   1
1) Rút gọn biểu thức P. 2) Tìm x để 1 P = . 3
Câu 3. (2,5 điểm) 1) Cho phương trình 2 x − (2m + )
1 x + 4m − 2 = 0 ( )
1 (với m là tham số).
a) Tìm tất cả giá trị của m để phương trình ( )
1 có hai nghiệm phân biệt.
b) Gọi x , x là hai nghiệm phân biệt của phương trình ( )
1 . Tìm tất cả giá trị của m để x , x là độ dài hai 1 2 1 2
cạnh của một hình chữ nhật có độ dài đường chéo bằng 13 .
2) Giải phương trình 6 2x + 5 + 4 x + 2 = 3x + 20.
Câu 4. (3,0 điểm)
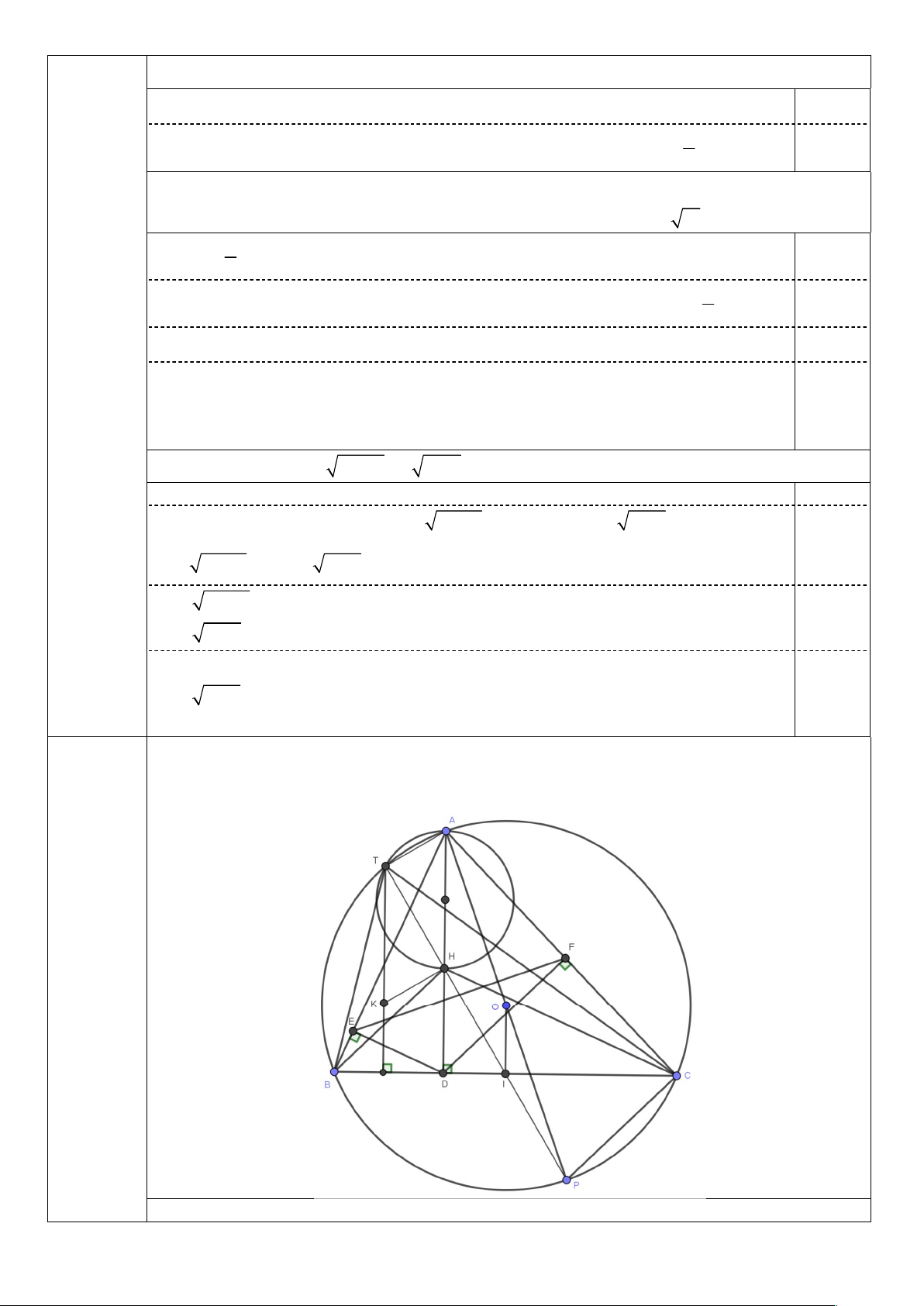
Cho tam giác ABC nhọn ( AB < AC) nội tiếp đường tròn tâm O, AD là đường cao. Gọi E, F lần lượt là hình
chiếu của D trên AB, AC.
1) Chứng minh tứ giác AEDF nội tiếp và AE.AB = AF.AC .
2) Gọi AP là đường kính của đường tròn (O) . Chứng minh AP vuông góc với EF.
3) Gọi H là trực tâm của tam giác ABC. Đường tròn đường kính AH cắt đường tròn (O) tại điểm thứ hai T.
Gọi K là trực tâm của tam giác BTC. Chứng minh tam giác HKT vuông tại H.
Câu 5. (1,0 điểm)  2 2
 4x + 3 − 2 y = y + 3 − 2 2x
1) Giải hệ phương trình  . 2
 x +1 + 3− x = 2 + y + 3− x
2) Xét hai số thực dương x, y thỏa mãn 6x + y = 2xy . Tìm giá trị nhỏ nhất của biểu thức 2 1 42 P = 3x + + + + ( x + y )2. 2 x x y
--------------- THCS.TOANMATH.com ---------------
Thí sinh không được sử dụng tài liệu khi làm bài. Giám thị coi thi không giải thích gì thêm./.
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . . . . . . .
Chữ ký giám thị 1: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Chữ ký giám thị 2: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM THI NAM ĐỊNH
ĐỀ THI TUYỂN SINH LỚP 10 TRƯỜNG THPT CHUYÊN
Năm học: 2023 - 2024
Môn thi: TOÁN (Chung) - Đề 1
Dành cho các học sinh thi vào các lớp chuyên tự nhiên
(Hướng dẫn chấm gồm: 04 trang) Câu Nội dung Điểm Câu 1:
(2,0 điểm) 1) Tính giá trị biểu thức P 
2024  2 2023  2025  2 2024 . P    2    2 2023 1 2024 1 0,25  2023 1  2024   1  2023  2024 . 0,25
2) Tìm tọa độ của điểm M là giao điểm của đường thẳng y  x 1 với trục Oy .
Tọa độ giao điểm là M 0;  1 . 0,5
3) Tính diện tích hình tròn ngoại tiếp tam giác vuông có cạnh huyền bằng 2 2 cm .
Gọi R là bán kính của đường tròn ngoại tiếp. 0,25
Từ giả thiết ta có 2R  2 2  R  2 .
Vậy diện tích của hình tròn là 2
S   R    2 2 cm  . 0,25
4) Tính thể tích của hình nón có đường sinh bằng 10 cm và bán kính đáy bằng 6 cm .
Gọi h là chiều cao của hình nón. Từ giả thiết ta có 2 2
h  10  6  h  8 . 0,25 1 1
Vậy thể tích của hình nón là 2 2
V   R h   .6 .8  96  3 cm  . 0,25 3 3 Câu 2:  x  2 x 1  1
(1,5 điểm) Cho biểu thức P     .
(với x  0 và x  1). x x 1 x  x  1 x 1 x 1  
1) Rút gọn biểu thức P . x  2  x  x  
1   x  x   1 1 P  . 0,25
 x  1x  x  1 x 1
x  2  x  x  x  x 1 1  .  0,25 x  
1  x  x   1 x 1  x  2 1 1  . 0,25
 x  1x  x  1 x 1 1  . 0,25 x  x 1 1
2) Tìm x để P  . 3 1 1 1 P     x  x  2  0 0,25 3 x  x  1 3  x  1  
 x  1l  . 0,25  x  2  Câu 3: 1) Cho phương trình 2
x  2m  
1 x  4m  2  0  
1 (với m là tham số). 1/4
(2,5 điểm) a) Tìm tất cả giá trị của m để phương trình  
1 có hai nghiệm phân biệt. 2
Ta có    m     m   2 2 1 4 4
2  4m 12m  9 . 0,25 3 Phương trình  
1 có hai nghiệm phân biệt khi và chỉ khi   0  m  . 0,25 2
b) Gọi x , x là hai nghiệm phân biệt của phương trình  
1 . Tìm tất cả giá trị của m để x , x 1 2 1 2
là độ dài hai cạnh của một hình chữ nhật có độ dài đường chéo bằng 13 . 3 Với m  thì phương trình  
1 có hai nghiệm phân biệt x  2, x  2m 1 . 0,25 2 1
Vì x , x là độ dài hai cạnh của một hình chữ nhật nên 2m 1  0  m  . 1 2 0,25 2
Ta có x  x  13  2  2m  2 2 2 2 2 1
 13  m  m  2  0 0,25 1 2
m  1l    .
m  2 tm 0,25  Vậy m  2 .
2) Giải phương trình 6 2x  5  4 x  2  3x  20 . Điều kiện: x  2  . 0,25
Phương trình trở thành 2x  5  6 2x  5  9   x  2  4 x  2  4  0     0,25   x 
 2   x   2 2 5 3 2 2  0 
 2x  5  3  0   0,25  x  2  2  0  x  2   
 x  2 tm .  x  2  2  0  0,25
Vậy nghiệm của phương trình là x  2 . Câu 4:
Cho tam giác ABC nhọn  AB  AC nội tiếp đường tròn tâm O , AD là đường cao. Gọi E , (3,0 điểm)
F lần lượt là hình chiếu của D trên AB , AC .
1) Chứng minh tứ giác AEDF nội tiếp và AE.AB  AF.AC . 2/4 Ta có  AED  90 ,  AFD  90 0,25
Xét tứ giác AEDF có  
AED  AFD  90  90  180 suy ra tứ giác AEDF nội 0,25 tiếp.
Trong tam giác vuông ABD có DE là đường cao suy ra 2
AE.AB  AD   1 . 0,25
Trong tam giác vuông ACD có DF là đường cao suy ra 2
AF.AC  AD 2 . 0,25
Từ (1) và (2) ta có AE.AB  AF.AC .
2) Gọi AP là đường kính của đường tròn O . Chứng minh AP vuông góc với EF . AE AF
Do AE.AB  AF.AC   , mà  BAC chung AC AB 0,25 Suy ra A  EF ∽ AC  B  
 AEF  ACB 0,25 Ta có   BAP  BCP 0,25 Suy ra     
AEF  BAP  ACB  BCP  ACP  90 0,25
Vậy AP vuông góc với EF .
3) Gọi H là trực tâm của tam giác ABC . Đường tròn đường kính AH cắt đường tròn O tại
điểm thứ hai T . Gọi K là trực tâm của tam giác BTC . Chứng minh tam giác HKT vuông tại H .
Ta có AH  BC , TK  BC  AH  TK . 0,25
Do BH  AC , PC  AC  BH  PC .
Do CH  AB , PB  AB  CH  PB .
Suy ra tứ giác BHCP là hình bình hành. 0,25 1
Gọi I là trung điểm BC , ta có OI  AH . 2 1 Tương tự OI 
TK  AH  TK . 2 0,25
Khi đó tứ giác AHKT là hình bình hành.  AT  HK . Mà  
ATH  90  THK  90 0,25
Vậy tam giác HKT vuông tại H . Câu 5: 2 2
 4x  3  2 y  y  3  2 2x    1
(1,0 điểm) 1) Giải hệ phương trình  . 2
 x 1  3  x  2  y  3  x 2  0  x  3 
Điều kiện:  y  0 .  2
y  3  x  0 
Phương trình (1) trở thành 2 2 4x  3 
y  3  2 2x  2 y  0 0,25  2x y 2x y     2x y   2   
 0  y  2x . 2 2  4x 3 y 3      
Thay vào phương trình (2) ta được 2
x 1  3  x  2  2x  3  x 0,25 2 t  4 Đặt 2 t 
x 1  3  x  2x  3  x  2 3/4 2 t  4 t  0 Khi đó 2 t  2 
 t  2t  0   2 t  2 
Với t  0 ta được x 1  3  x  0vn . x  1  l 
Với t  2 ta được x 1  3  x  2   x  
1 3  x  0   .
x  3tm 
Với x  3  y  6 .
Vậy nghiệm của hệ phương trình là  ; x y  3;6 .
2) Xét hai số thực dương x , y thỏa mãn 6x  y  2xy . Tìm giá trị nhỏ nhất của biểu thức 2 1 42 P  3x   
  x  y 2 . 2 x x y 2 1 42
Ta có P  4x    y   2 xy 2 x x y 1 6
Do x  0, y  0 và 6x  y  2xy nên   2 0,25 x y
Mặt khác ta có 2xy  6x  y  2 6xy  xy  6  2   1 6   36 
Khi đó P  2x  2x     y 
 2 xy  3.2  2  2.6  2 6  2       x  x y y      P  20  2 6 . 0,25
Dấu bằng xảy ra khi x  1, y  6 .
Vậy giá trị nhỏ nhất của biểu thức P là 20  2 6 . Chú ý:
- Nếu thí sinh làm đúng, cách giải khác với hướng dẫn chấm, phù hợp kiến thức của chương trình
THCS thì tổ chấm thống nhất cho điểm thành phần đảm bảo tổng điểm như hướng dẫn quy định.
- Tổng điểm toàn bài không làm tròn.
---------- HẾT ---------- 4/4
Document Outline

• de-thi-vao-10-chuyen-mon-toan-chung-tn-nam-2023-2024-so-gddt-nam-dinh
• 2. Đáp án đề chung TN