Đề thi vào 10 chuyên môn Toán (chuyên) năm 2021 – 2022 sở GD&ĐT Lâm Đồng

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH VÀO LỚP 10 CHUYÊN LÂM ĐỒNG NĂM HỌC 2021 – 2022 ĐỀ CHÍNH THỨC Môn thi: TOÁN – CHUYÊN (Đề thi có 01 trang)
Thời gian làm bài: 120 phút
Khóa thi ngày: 9, 10, 11/6/2021 Câu 1. (2,0 điểm)
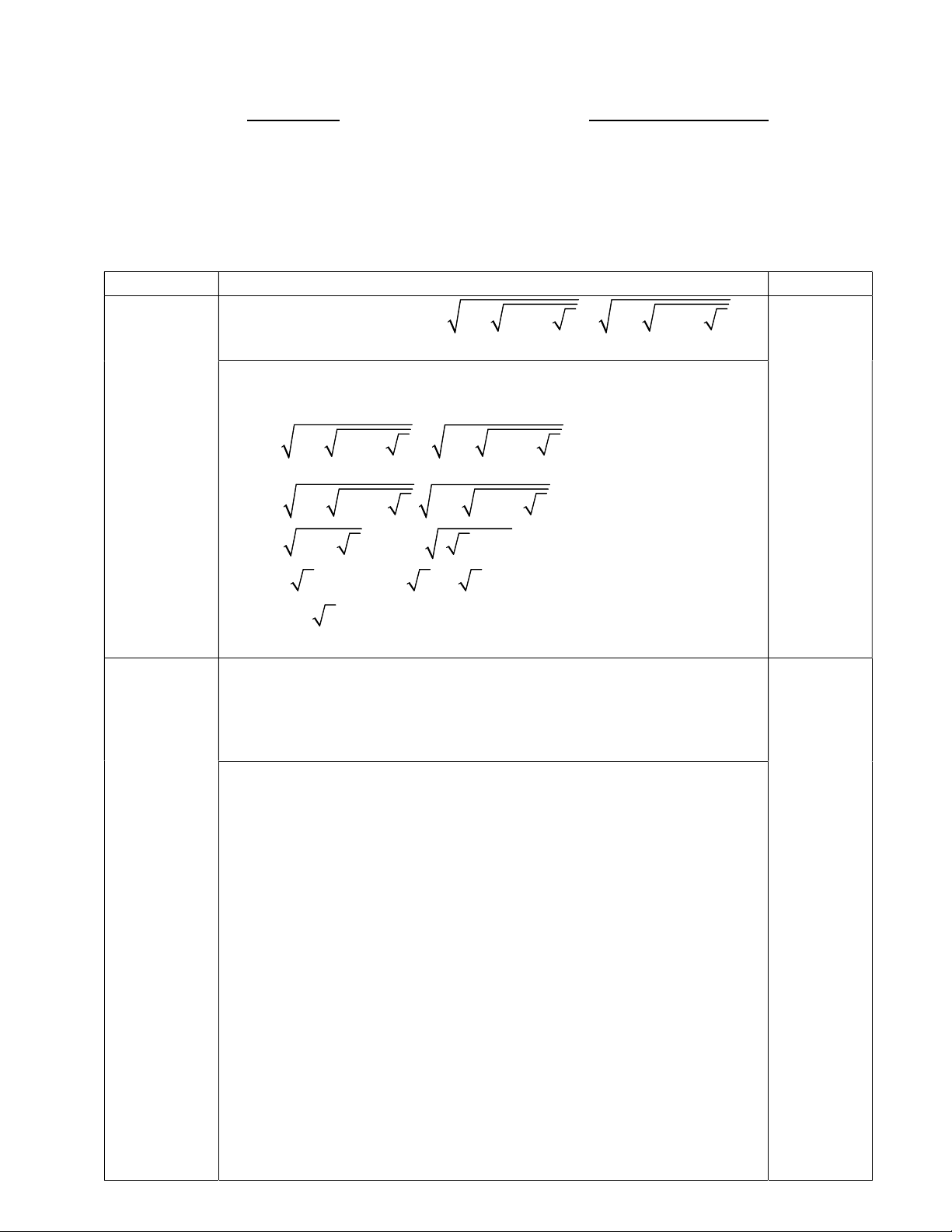
Tính giá trị biểu thức: A  4  10  2 5  4  10  2 5 . Câu 2. (2,0 điểm) Cho 2 3 4 2021 2022
B  2  2  2  2  ...  2
 2 . Chứng minh rằng B  2
không phải là số chính phương. Câu 3. (2,5 điểm)
Cho tam giác ABC, đường cao AH H  BC.Biết BC  AB  2cm, AC  10cm và  0
CAH  30 . Tính diện tích tam giác ABC. Câu 4. (2,0 điểm)
Cho a,b,c là các số nguyên thỏa mãn 3
a  b  20c  c . Chứng minh rằng 3 3 3
a  b  c chia hết cho 6. Câu 5. (2,0 điểm)
Trường THCS X có 60 giáo viên. Tuổi trung bình của tất cả thầy
giáo và cô giáo là 42 tuổi. Biết rằng tuổi trung bình của các thầy
giáo là 50, tuổi trung bình của các cô giáo là 38. Hỏi trường THCS
X có bao nhiêu thầy giáo, bao nhiêu cô giáo? 2
 2x  y  3  x  9  0 Câu 6. (1,5 điểm)
Giải hệ phương trình:  2 y  2xy  9  0. Câu 7. (2,0 điểm) Cho phương trình: 2 x  m   2
1 x  m  2  0 ( x là ẩn, m là tham số).
Tìm giá trị của m để phương trình có hai nghiệm trái dấu thỏa mãn
2 x  x  4 (biết x  x ). 1 2 1 2 Câu 8. (2,5 điểm)
Cho hình vuông ABCD . Vẽ đường tròn tâm O đường kính BC và đường tròn  ;
A AB chúng cắt nhau tại một điểm thứ hai là E ( E
khác B ). Tia CE cắt AD tại điểm F. Chứng minh rằng F là trung điểm của A . D Câu 9. (1,5 điểm) Cho a, ,
b c là các số dương và a  b  c  6. Tìm giá trị nhỏ nhất 3 3 3 a b c biểu thức: P    . 2 2 2 2 2 2 a  4ab  b b  4bc  c c  4ca  a
Câu 10. (2,0 điểm) Cho hình bình hành ABCD có  0
BAD  90 . Gọi H là chân đường
vuông góc kẻ từ A đến BC. Đường trung tuyến kẻ từ C của tam
giác ABC cắt đường tròn ngoại tiếp tam giác ABC tại K . Chứng
minh rằng bốn điểm K, H , D, C cùng thuộc một đường tròn.
------------ HẾT ------------
Họ tên thí sinh:……………………………………Số báo danh:……………………...
Giám thị 1:……………………Ký tên………Giám thị 2: ………………Ký tên:……...
SỞ GIÁO DỤC VÀ ĐÀO TẠO KÌ THI TUYỂN SINH VÀO LỚP 10 CHUYÊN LÂM ĐỒNG NĂM HỌC 2021 – 2022 Môn thi: TOÁN – CHUYÊN
(Hướng dẫn chấm gồm có 06 trang) Khóa thi ngày: 9, 10, 11/6/2021
ĐÁP ÁN, HƯỚNG DẪN CHẤM ĐỀ CHÍNH THỨC CÂU HƯỚNG DẪN CHẤM ĐIỂM Câu 1     
(2,0 điểm ) Tính giá trị biểu thức: A  4 10 2 5 4 10 2 5 . - Lập luận : A  0 0,5 điểm 2 2   A 
4  10  2 5  4  10  2 5   0,5 điểm  
 8  2 4  10  2 5 . 4  10  2 5 2
 8  2 6  2 5  8  2. ( 5 1) 0,5 điểm 2
 8  2( 5 1)  6  2 5  ( 5 1)  A 1 5. 0,5 điểm Câu 2       (2,0 điểm ) Cho 2 3 4 2021 2022 B  2 2 2 2 ... 2 2 . Chứng minh rằng
B  2 không phải là số chính phương. - Biến đổi: 2 3 4 2021 2022
B  2  2  2  2  ...  2  2 2 3 4 2021 2022
 2B  22  2  2  2  ... 2  2  2 3 2022 2023
 2B  2  2  ...  2  2 0,5 điểm - Tính được: 2023 2023 2B  B  2  2  B  2  2 0,5 điểm - Tính được: 2023 2023     B  2 2 2 2 2 0,5 điểm
- Lập luận được: Vì 2023 2
là lũy thừa với số mũ lẻ nên 2023 2
không là số chính phương.
Vậy B  2 không là số chính phương 0,5 điểm Câu 3
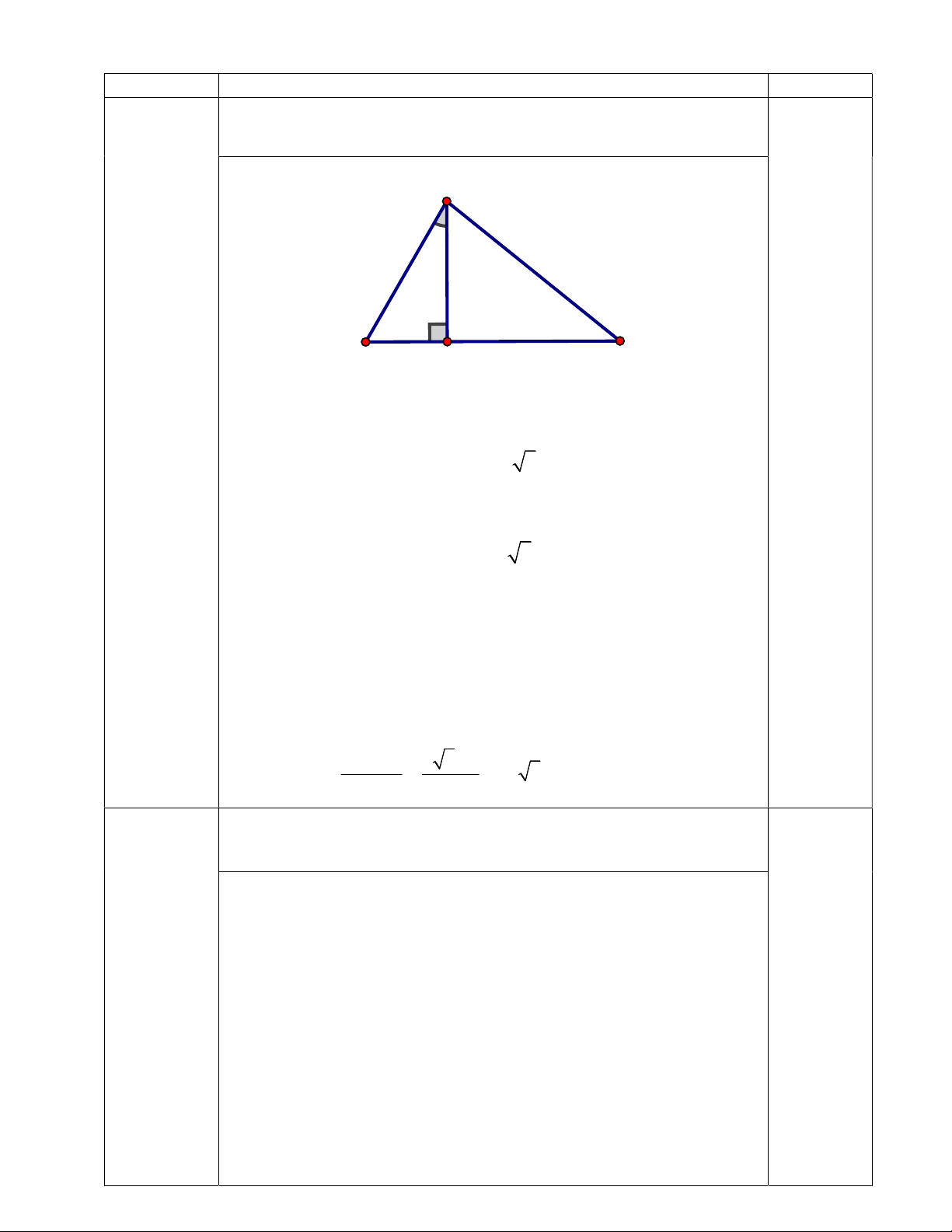
Cho tam giác ABC, đường cao AH H  BC. Biết AC 10c , m
(2,5 điểm ) BC  AB  2cm và  0
CAH  30 . Tính diện tích tam giác ABC. A 10cm 30° C H B - Tính được: 0 CH  AC.sin 30  5cm 0 AH  AC.cos30  5 3cm 0,5 điểm - Viết được: 2 2 2 AB  HB  AH 2
AB  BC  5  5 32 2 0,5 điểm
- Lập luận : BC  AB  2cm  AB  BC  2 0,5 điểm
 BC  2  BC  2 2 5  75        
BC 2 BC 5BC 2 BC 5 75 0,5 điểm - Tính được: BC 16 cm AH.BC 5 3.16 2 0,5 điểm - Vậy S    40 3 ABC cm  2 2 Câu 4
Cho a,b,c là các số nguyên thỏa mãn 3 a  b  20c  c . (2,0 điểm ) Chứng minh rằng 3 3 3
a  b  c chia hết cho 6. - Biến đổi được: 3 3
a  b  20c  c  a  b  c  c  c 18c 0,5 điểm
 a  b  c  cc   1 c   1 18c
- Chứng minh được:  a  b  c  cc   1 c   1 18c6 0,5 điểm - Mặt khác: 3 3 3
a  b  c  (a  b  c)
 (a 1)a(a 1)  (b1)b(b1)  (c1)c(c1)6 0,5 điểm - Lập luận kết luận 3 3 3
a  b  c chia hết cho 6 0,5 điểm Câu 5
Trường THCS X có 60 giáo viên. Tuổi trung bình của tất cả
(2,0 điểm ) thầy giáo và cô giáo là 42 tuổi. Biết rằng tuổi trung bình của
các thầy giáo là 50, tuổi trung bình của các cô giáo là 38. Hỏi
trường THCS X có bao nhiêu thầy giáo, bao nhiêu cô giáo?
- Gọi x và y lần lượt là số cô giáo và số thầy giáo của trường *
THCS X x, y  N ; x, y  60 0,5 điểm
- Lập luận được pt: x  y  60 0,25 điểm 38x  50 y - Lập luận được pt:  42 60 0,5 điểm x  y  60  x  40 - Giải hệ pt:    38x 50 y   42  y  20 0,5 điểm  60 0,25 điểm
- Trả lời: Cô giáo : 40 , thầy giáo : 20 Câu 6 2
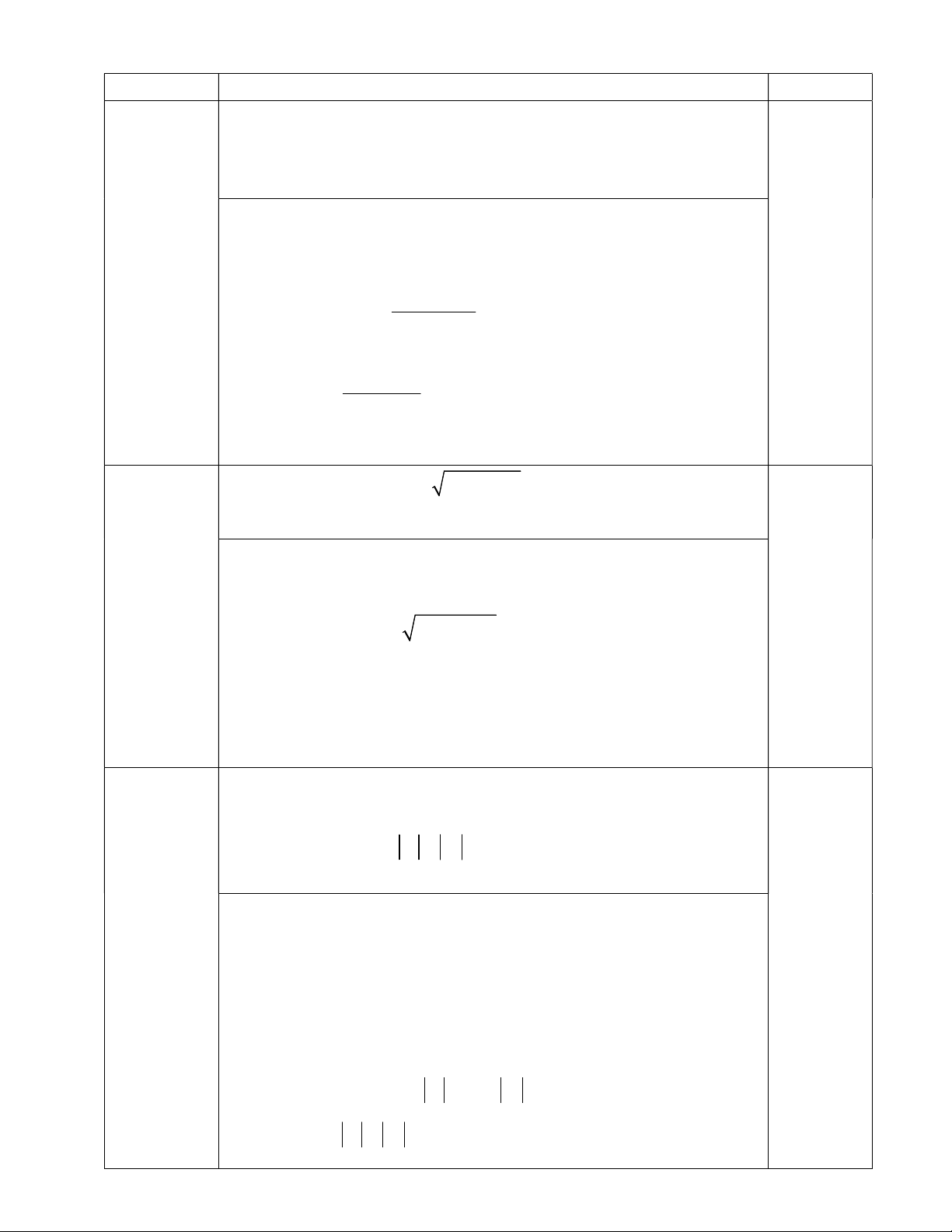
 2x  y 3  x 9  0  1
(1,5 điểm ) Giải hệ phương trình:  2 y  2xy  9  0.  2
- Điều kiện 2x  y  3  0 , 0,25 điểm
- Phương trình (2)   y  x2 2  x  9 0,25 điểm 0,25 điểm - Phương trình   
x  y    y  x2 1 2 3  0 2x  y  3  0 x  3 0,5 điểm          y x 0 y x
- Kiểm tra điều kiện và kết luận hệ phương trình có nghiệm 3;3 0,25 điểm Câu 7 Cho phương trình: 2 x  m   2
1 x  m  2  0 (*) ( x là ẩn, m là (2,0 điểm )
tham số). Tìm giá trị của m để phương trình có hai nghiệm
trái dấu thỏa mãn 2 x  x  4 (biết x  x ). 1 2 1 2
- Lập luận được phương trình (*) có hai nghiệm trái dấu thì P < 0 0,5 điểm ac   2
1. m  2  0 nên phương trình có hai nghiệm trái dấu với mọi giá trị m.
- Do phương trình (*) có hai nghiệm phân biệt trái dấu và x  x 1 2
Suy ra x  0, x  0  x  x , x  x 1 2 1 1 2 2 0,5 điểm
do đó từ gt: 2 x  x  4  2x  x  4 1 1 2   1 2 x  x 1 m (2) 0,25 điểm
- Theo định lí Viet ta có: 1 2  2 x .x  m  2 (3)  1 2 x  x 1 m (2) x  m  5 - Giải hệ 1 2 1    0,25 điểm 2x  x  4 (1) x  6  2m  1 2  2
Mà x  0  x nên ta được m  3. 1 2
- Thay x  m  5, x  6  2m vào (3) ta được phương trình: 1 2 0,25 điểm   2 m
(m 5)(6  2m)  m  2 2   . m  14 0,25 điểm
- Kết hợp m  3 ta được m  2 thỏa yêu cầu bài toán. Câu 8
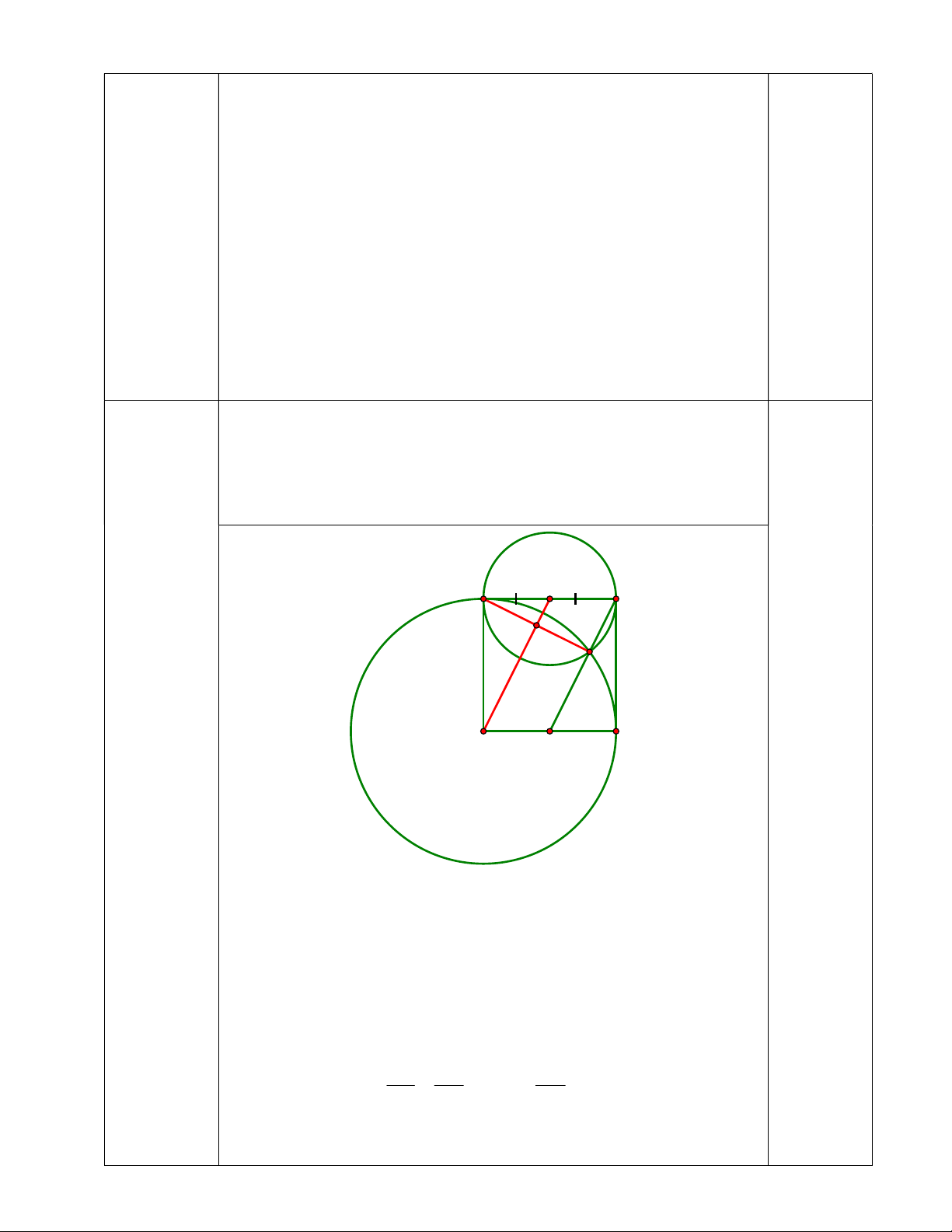
Cho hình vuông ABCD . Vẽ đường tròn tâm O đường kính
(2,5 điểm ) BC và đường tròn ;
A AB chúng cắt nhau tại một điểm thứ hai
là E ( E khác B). Tia CE cắt AD tại điểm F. Chứng minh rằng
F là trung điểm của AD . O B C H E A D F 0,5 điểm
- Kẻ đoạn nối tâm OA và dây chung BE  OA  BE 0,5 điểm
- Chứng minh được: BE  CF 0,5 điểm
- Chứng minh được:OA / /CF 0,5 điểm
- Chứng minh được tứ giác AOCF là hình bình hành  OC  FA . BC AD AD 0,5 điểm - Lập luận: từOC    AF   F là trung điểm của 2 2 2 AD . Câu 9
Cho a, b, c là các số dương và a  b  c  6. Tìm giá trị nhỏ
(1,5 điểm ) nhất biểu thức: 3 3 3 a b c P    . 2 2 2 2 2 2 a  4ab  b b  4bc  c c  4ca  a 3 a b
Với a,b  0 , ta chứng minh  a  . 2 2 a  b 2 1  1  0,25 điểm - Áp dụng: a  b2 2 2  0  a  b  2ab   2 2 a  b 2ab Khi đó: 3 2 2 2 2 2 a a(a  b )  ab ab ab b   a   a   a  2 2 2 2 2 2 a  b a  b a  b 2ab 2 0,25 điểm 3 b c 3 c a   b  ;  c  2 2 b  c 2 2 2 c  a 2
Cộng vế theo vế ba bất đẳng thức trên ta có: 3 3 3 a b c a  b  c    2 2 2 2 2 2 a  b b  c c  a 2 2 2 2 0,25 điểm
- Áp dụng:a  b  0  2a  b   4ab Ta có: 3 3 3 a a 1 a   . ; 2 2 2 2 2 2 2 2 a  4ab  b a  2(a  b )  b 3 a  b 3 3 3 b b 1 b 0,25 điểm   . ; 2 2 2 2 2 2 2 2 b  4bc  c b  2(b  c )  c 3 b  c 3 3 3 c c 1 c   . 2 2 2 2 2 2 2 2 c  4ac  a c  2(c  a )  a 3 c  a
Cộng vế theo vế ba bất đẳng thức trên ta có: 3 3 3 0,25 điểm a b c   2 2 2 2 2 2 a  4ab  b b  4bc  c c  4ca  a 3 3 3 1  a b c  a  b  c     1  2 2 2 2 2 2  3  a  b b  c c  a  6 0,25 điểm
-Vậy giá trị nhỏ nhất của P là 1, dấu “=” xảy ra khi a  b  c  2. Câu 10
Cho hình bình hành ABCD có  0 BAD  90 .Gọi H là chân
(2,0 điểm ) đường vuông góc kẻ từ A đến BC . Đường trung tuyến kẻ từ
C của tam giác ABC cắt đường tròn ngoại tiếp tam giác ABC
tại K .Chứng minh rằng bốn điểm K, H, D, C cùng thuộc một đường tròn. K O M A B C D H
Gọi M là trung điểm AB .
Để chứng minh bốn điểm K, H , D, C cùng thuộc một đường tròn, ta đi chứng minh  DKH   DCH . - Chứng minh được:  DCH   ABC   AKC 0,5 điểm
Khi đó ta đi chứng minh  DKA   HKM .
Bài toán được hoàn thành nếu ta chứng minh được tam giác
DKA đồng dạng tam giác HKM. - Chứng minh được:  KAD   KMH 0,5 điểm Ta có:  KAD  180    KAC   180    DAC    KBC   ACH mà  KMH   MHC   MCH   MBC   MCA   ACH   KBC   ACH Suy ra  KAD   KMH (1) - Chứng minh được: K  MA # B  MC KA BC AD AK MK      (2) KM BM MH AD MH 0,5 điểm
- Từ (1) và (2) suy ra DKA # H  KM   DKA   HKM Mà  DKH   DKA   AKH   HKM   AKH   AKC   DKH   DCH
Và kết luận bốn điểm K, H, D, C cùng thuộc một đường tròn. 0,5 điểm
(Lưu ý: Học sinh giải cách khác đúng giám khảo phân bước cho điểm tương ứng) …………Hết……….