Đề thi vào 10 môn Toán (chuyên) năm 2021 – 2022 trường chuyên Lê Hồng Phong – Nam Định

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH VÀO LỚP 10 NAM ĐỊNH
TRƯỜNG THPT CHUYÊN LÊ HỒNG PHONG NĂM HỌC 2021-2022.
Môn thi: Toán (chuyên)
Thời gian làm bài:150 phút. (Đề thi gồm: 01 trang) Câu 1 (2,0 điểm). a) Cho a, ,
b c ∈  thỏa mãn a + b + c = 0 và 2 2 2
a + b + c =1. Tính giá trị của biểu thức 2 2 2 2 2 2
S = a b + b c + c a .
b) Cho đa thức bậc hai P(x) thỏa mãn P( )
1 =1, P(3) = 3, P(7) = 31. Tính giá trị của P(10). Câu 2 (2,0 điểm). 2 2  x  x a) Giải phương trình 2 7 x + +  4 = ⋅   x +1 x +1 x(2x + )
1 = y(x + y − 2) +  1
b) Giải hệ phương trình 
4 x + 3 + 2 y + 2 =11− .x
Câu 3 (3,0 điểm). Cho tam giác nhọn ABC ( AB < AC) nội tiếp đường tròn (O) . Đường phân giác trong của 
BAC cắt đường tròn (O) tại D ( D ≠ A). Trên cung nhỏ AC của đường tròn (O)
lấy điểm G khác C sao cho AG > GC ; một đường tròn có tâm là K đi qua A, G và cắt đoạn
thẳng AD tại điểm P nằm bên trong tam giác ABC . Đường thẳng GK cắt đường tròn (O) tại
điểm M ( M ≠ G ).
a) Chứng minh các tam giác KPG , ODG đồng dạng với nhau.
b) Chứng minh GP, MD là hai đường thẳng vuông góc.
c) Gọi F là giao điểm của hai đường thẳng OD và KP , đường thẳng qua A và song song
với BC cắt đường tròn (K ) tại điểm E ( E ≠ A). Chứng minh rằng tứ giác DGFP là tứ giác nội tiếp và  0 EGF = 90 . Câu 4 (1,5 điểm).
a) Tìm tất cả các cặp số nguyên dương ( ; x y) thỏa mãn 2 2
x y ( y − x) 2 = 5xy − 27 . b) Cho p , ,
p …, p là các số nguyên tố lớn hơn 3. Chứng minh rằng 2 2 2
p + p ++ p 1 2 12 1 2 12 chia hết cho 12. Câu 5 (1,5 điểm).
a) Cho a,b,c > 0 và a + + +
+ b + c =1. Chứng minh rằng a bc b ca c ab + + ≥ 2 . b + c c + a a + b b) Xét hai tập hợp ,
A B khác ∅ thỏa mãn A B = ∅ và *
A  B =  . Biết rằng A có vô
hạn phần tử và tổng của mỗi phần tử thuộc A với mỗi phần tử thuộc B là phần tử thuộc B . Gọi
x là phần tử bé nhất thuộc B thỏa mãn x ≠ 1. Hãy tìm x. --------- HẾT ---------
Họ và tên thí sinh:……………………………..
Họ tên, chữ ký GT 1:……………………………….
Số báo danh:…………………………………..
Họ tên, chữ ký GT 2:………………………...……..
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM THI NAM ĐỊNH
ĐỀ THI TUYỂN SINH VÀO LỚP 10 TRƯỜNG THPT CHUYÊN
Năm học 2021– 2022.
Môn thi: TOÁN (chuyên)
(Hướng dẫn chấm gồm: 05 trang) Câu 1 (2,0 điểm). a) Cho a, ,
b c ∈  thỏa mãn a + b + c = 0 và 2 2 2
a + b + c =1. Tính giá trị của biểu thức 2 2 2 2 2 2
S = a b + b c + c a .
b) Cho đa thức bậc hai P(x) thỏa mãn P( )
1 =1, P(3) = 3, P(7) = 31. Tính giá trị của P(10). Ý Nội dung Điểm
+ Ta có = (a + b + c)2 2 2 2 0
= a + b + c + 2(ab + bc + ca) =1+ 2(ab + bc + ca) 0,5 suy ra 1
ab + bc + ca = − . 1a 2
1,0đ + Từ (ab +bc + ca)2 2 2 2 2 2 2
= a b + b c + c a + 2abc(a + b + c) 0,5 suy ra 2 2 2 2 2 2 1
S = a b + b c + c a = . 4
a + b + c = P( ) 1 =1  + Đặt ( ) 2
P x = ax + bx + c thì có hệ 9
 a + 3b + c = P(3) = 3 . 0,5
49a +7b+c = P  (7) = 31
1b + Giải hệ được a =1, b = 3 − , c = 3. 0,25
1,0đ + Suy ra P(x) 2
= x − 3x + 3 nên P( ) 2 10 =10 − 3.10 + 3 = 73. 0,25 Cách khác:
+ Thấy P(x) − x có nghiệm là x =1, x = 3 nên có P(x) − x = a(x − ) 1 (x − 3).
+ Từ P(7) = 31 nên 31− 7 = a(7 − ) 1 (7 − 3) ⇔ a =1.
+ Vậy P(x) = (x − )
1 (x − 3) + x ⇒ P(10) = 73. Câu 2 (2,0 điểm). 2 2  x  x a) Giải phương trình 2 7 x + +  4 =  .  x +1 x +1 x(2x + )
1 = y(x + y − 2) +  1
b) Giải hệ phương trình 
4 x + 3 + 2 y + 2 =11− .x Ý Nội dung Điểm
+ Điều kiện xác định x ≠ 1 − . 2a 2 2 2  x  7x 2x
1,0đ + PT cho tương đương với x − +  4 = −   x +1 x +1 x +1 0,25 Trang 1/5-Đáp án 2 2 2  x  x ⇔ − 5. + 4 =   0  x +1 x +1 2 x 2 ⇔ = 1 x (1) hoặc = 4 (2) 0,25 x +1 x +1 1 5 + Giải (1) được x ± = . 0,25 2
+ Giải (2) được x = 2 ± 2 2 .  ±  0,25
Tập nghiệm của phương trình là 1 5  ;2 2 2 ±  2   
Cách khác: Quy đồng, rút gọn được 4 3 2
x − 5x − x + 8x + 4 = 0 ⇔ ( 2 x − x − )( 2
1 x − 4x − 4) = 0  2 1± 5
x − x −1 = 0 x = ⇔  ⇔ 2 (thỏa mãn điều 2 x 4x 4 0  − − = x = 2 ± 2 2 kiện) x(2x + )
1 = y(x + y − 2) +  1 (1) Xét hệ 
4 x + 3 + 2 y + 2 =11− x (2) 0,25
+ Điều kiện xác định: x ≥ 3 − và y ≥ 2 − . + Ta có ( ) 2
⇔ y + y(x − ) 2 1
2 − 2x − x +1 = 0  y = x + 0,25
⇔ ( y − − x)( y − + x) 1 1 1 2 = 0 ⇔  .  y = 1− 2x
+ Với y = x +1, thay vào (2) ta được 2b 11  − x ≥ 0 6 x 3 11 x  + = − ⇔  ⇔ x = 29 − 6 23 . 1,0đ 36
 (x + 3) = (11− x)2 0,25
Khi x = 29 − 6 23 thì y = x +1 = 30 − 6 23 (thỏa mãn điều kiện).
+ Với y =1− 2x , thay vào (2) ta được 2 2
4 x + 3 + 2 3 − 2x =11− x ⇔ ( x + 3 − 2) + ( 3− 2x − ) 1 = 0 0,25  x + 3 = 2 ⇔ 
⇔ x =1. Khi đó có y =1− 2x = 1
− (thỏa mãn điều kiện).  3− 2x =1 Trang 2/5-Đáp án
+ Kết luận: Hệ cho có đúng hai bộ nghiệm ( ;
x y) là (29 − 6 23;30 − 6 23), (1; )1 − .
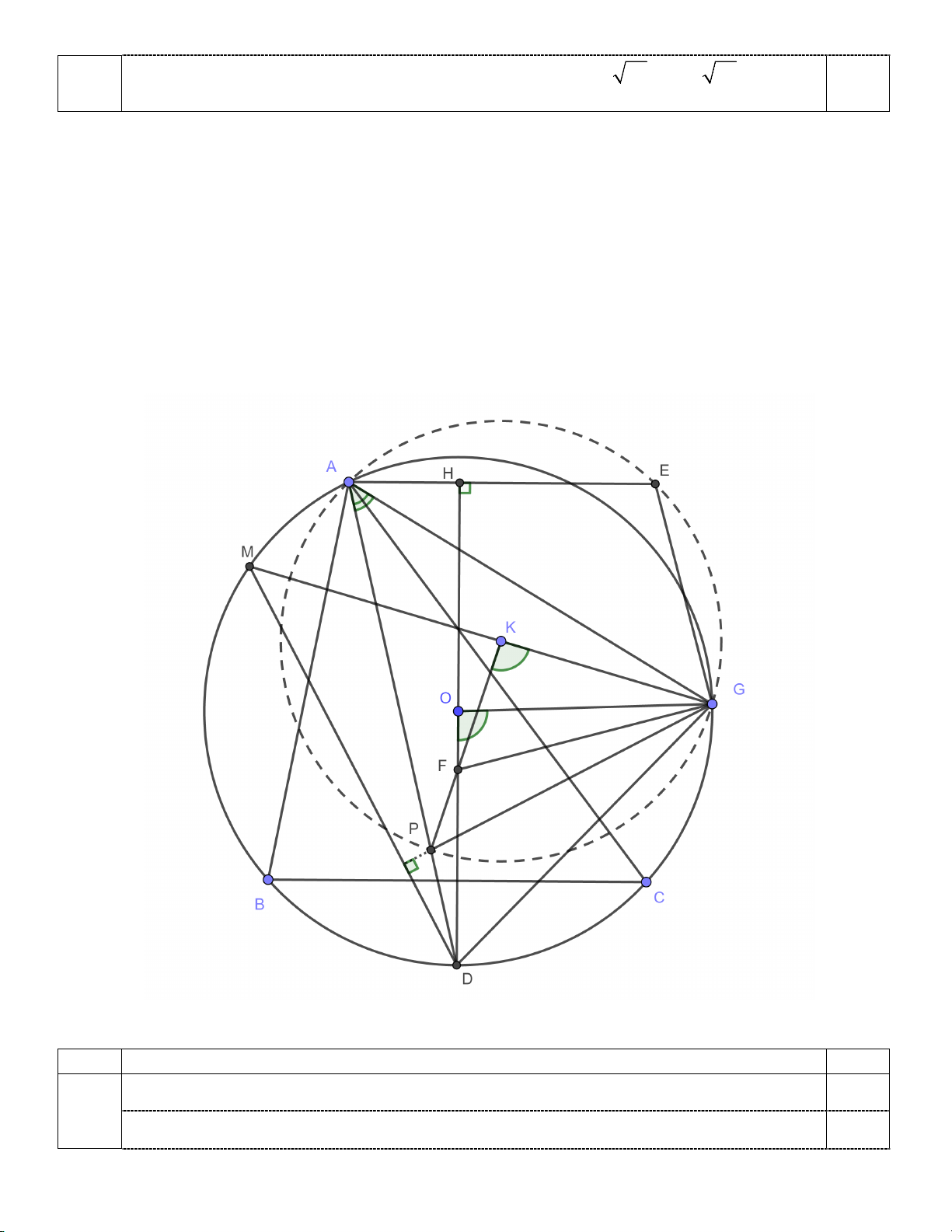
Câu 3 (3,0 điểm). Cho tam giác nhọn ABC ( AB < AC) nội tiếp đường tròn (O) . Đường phân giác trong của 
BAC cắt đường tròn (O) tại D ( D ≠ A). Trên cung nhỏ AC của đường tròn (O) lấy
điểm G khác C sao cho AG > GC ; một đường tròn có tâm là K đi qua A, G và cắt đoạn thẳng AD
tại điểm P nằm bên trong tam giác ABC . Đường thẳng GK cắt đường tròn (O) tại điểm M ( M ≠ G ).
a) Chứng minh các tam giác KPG , ODG đồng dạng với nhau.
b) Chứng minh GP,MD là hai đường thẳng vuông góc.
c) Gọi F là giao điểm của hai đường thẳng OD và KP , đường thẳng qua A và song song với
BC cắt đường tròn (K ) tại điểm E ( E ≠ A). Chứng minh rằng tứ giác DGFP là tứ giác nội tiếp và  0 EGF = 90 . Ý Nội dung Điểm
3a + Xét đường tròn (O) có  =  DOG 2DAG . 0,25
1,0đ + Xét đường tròn (K) có  =  PKG 2PAG . 0,25 Trang 3/5-Đáp án Suy ra  =  DOG PKG (1). 0,25
+ Tam giác PKG cân ở K và tam giác DOG cân ở O (2).
Từ (1) và (2) suy ra hai tam giác này đồng dạng với nhau. 0,25 GKP 3b Có  =   0 0 = − = −  MGP KGP 90 90 DAG 0,5 1,0đ 2 Mặt khác  =  DAG DMG nên  +  0
MGP DMG = 90 , suy ra GP ⊥ DM 0,5 Ta có  =  =  = 
FPG KPG ODG FDG , suy ra tứ giác DGFP nội tiếp 0,5 = = 3c Suy ra  
DFG DPG . Tứ giác APGE nội tiếp nên   DPG AEG . 1,0đ Suy ra  =  AEG DFG hay  = 
HEG DFG với H là giao điểm của OD và AE . 0,25
Suy ra tứ giác HEGF nội tiếp.
OD ⊥ BC nên OD ⊥ AE , suy ra  0 FHE = 90 , do đó  0 = −  0 EGF 180 FHE = 90 . 0,25 Câu 4 (1,5 điểm).
a) Tìm tất cả các cặp số nguyên dương ( ; x y) thỏa mãn 2 2
x y ( y − x) 2 = 5xy − 27 .
b) Cho p , p ,…, p là các số nguyên tố lớn hơn 3. Chứng minh rằng 2 2 2
p + p ++ p chia 1 2 12 1 2 12 hết cho 12. Ý Nội dung Điểm + Giả sử có *
x, y ∈  thỏa mãn yêu cầu. Ta có 2 y ( 3 2
x − x y + 5x) = 27 (1). 0,25 Suy ra 27 chia hết cho 2 y nên 2 y ∈{1; } 9 hay y ∈{1; } 3 .
+ Xét y =1, thay vào (1) có 3 2
x − x + x = ⇔ x( 2 5 27
x − x + 5) = 27. 4a
0,75đ Điều này chứng tỏ x là ước nguyên dương của 27 và có 27
5x ≤ 27 ⇔ x ≤ , suy ra 0,25 5
x =1 hoặc x = 3. Thử trực tiếp hai trường hợp này thấy không thỏa mãn.
+ Xét y = 3, thay vào (1) có 3 2
x − x + x − = ⇔ (x − )( 2 3 5 3 0
2 x − 2x + 3) = 0 ⇔ x =1. 0,25 Vậy ( ; x y) = (1;3) .
+ Với p là số nguyên tố lớn hơn 3 nên có dạng p = k ± ( * 6 1 k ∈ ) 0,25 4b Suy ra 2 2
p −1 = 36k ±12k chia hết cho 12. 0,25
0,75đ + Áp dụng có ( 2 p − ) 1 + ( 2 p − ) 1 + ...+ ( 2
p −1 chia hết cho 12 1 2 12 ) 0,25 Suy ra 2 2 2
p + p ++ p chia hết cho 12. 1 2 12 Cách viết khác:
+ Từ p = k ± ( *
3 1 k ∈  ) suy ra 2 2
p −1 = 9k ± 6k chia hết cho 3.
+ Từ p = k ± ( * 4
1 k ∈  ), khi đó có 2 2
p −1 =16k ± 8k chia hết cho 4. Suy ra 2 p −1 chia hết cho 12. + Áp dụng suy ra 2 2 2
p + p ++ p chia hết cho 12. 1 2 12 Trang 4/5-Đáp án Câu 5 (1,5 điểm).
a) Cho a,b,c > 0 và a + b + c =1. Chứng minh rằng a + bc b + ca c + ab + + ≥ 2 . b + c c + a a + b b) Xét hai tập hợp ,
A B khác ∅ thỏa mãn A B = ∅ và *
A  B =  . Biết rằng A có vô hạn
phần tử và tổng của mỗi phần tử thuộc A với mỗi phần tử thuộc B là phần tử thuộc B . Gọi x là
phần tử bé nhất thuộc B thỏa mãn x ≠ 1. Hãy tìm x. Ý Nội dung Điểm
a + bc a(a + b + c) + bc (a + b)(a + c) + Ta có = = . b + c b + c b + c
Tương tự thì BĐT cần chứng minh được viết lại thành 0,25
(a + b)(a + c) (b + c)(b + a) (c + a)(c + b) + + ≥ 2 . b + c c + a a + b + Theo BĐT Cauchy có 5a
(a +b)(a +c) (b+c)(b+ a)
(a +b)(a +c) (b+c)(b+ a) 0,25 + ≥ 2 . = 2(a + b) (1) 0,75đ b + c c + a b + c c + a
(b + c)(b + a) (c + a)(c + b) Tương tự có +
≥ 2(b + c) (2) c + a a + b
(a + b)(a + c) (c + a)(c + b) +
≥ 2(c + a) (3) . 0,25 b + c a + b
Cộng vế các BĐT (1), (2), (3) suy ra ĐPCM.
+ Chứng minh 1∈ B :
Giả sử ngược lại, 1∈ A, khi đó với x ∈ B có x +1∈ B . 0,25 Có 1∈ ,
A x +1∈ B suy ra x + 2 =1+(x + )1 thuộc B . Cứ như vậy có x, x +1, x + 2,....
đều nằm trong B nên suy ra A là tập hữu hạn, mâu thuẫn. Vậy có 1∈ B .
+ Xét x ≥ 4 : Do 1 < x − 2 < x nên từ tính bé nhất của x trong B suy ra x − 2∈ A , suy
5b ra x −1 = (x − 2) +1 thuộc B, điều này lại mâu thuẫn với tính bé nhất của x trong B. 0,25
0,75đ Vậy phải có x = 2 hoặc x = 3.
+ Với x = 2 , cách chọn A là tập các số nguyên dương chia hết cho 3 và B là tập
hợp các số nguyên dương không chia hết cho 3 thỏa mãn yêu cầu.
Với x = 3, cách chọn A là tập hợp các số nguyên dương chẵn và B là tập hợp các 0,25
số nguyên dương lẻ thỏa mãn yêu cầu.
Tóm lại x = 2 hoặc x = 3. Chú ý:
- Nếu thí sinh làm đúng mà cách giải khác với đáp án và phù hợp kiến thức của chương trình THCS thì tổ
chấm thống nhất cho điểm thành phần đảm bảo tổng điểm như hướng dẫn quy định. Trang 5/5-Đáp án
- Tổng điểm toàn bài không làm tròn.
---------- HẾT ---------- Trang 6/5-Đáp án
Document Outline

• 39. NAM ĐỊNH. Đề Toan chuyen 2021-chuan
• 39. NAM ĐỊNH. Dap an Toan chuyen 2021-chuan