Đề thi vào lớp 10 chuyên môn Toán năm 2020 – 2021 sở GD&ĐT Bình Dương (chuyên)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT CHUYÊN BÌNH DƯƠNG
NĂM HỌC 2020 – 2021 -------------------- Môn Toán chuyên Ngày thi 10/7/2020
Thời gian 150 phút (không kể thời gian phát đề) Câu 1. (3,0 điểm)
a) Giải phương trình  x   x   2 2020
2019 1 x  x  2019 2020  4039. 1 1 1
b) Cho hai số thực m, n khác 0 thỏa mãn
  . Chứng minh rằng phương trình: m n 2
 2x mx  n  2
x  nx  m  0 luôn có nghiệm. Câu 2. (1,5 điểm)
Với các số thực x, y thay đổi thỏa mãn 1 x  y  5. Tìm giá trị nhỏ nhất của biểu thức: P   2 2
2 x  y  4x  y  xy 7. Câu 3. (2,0 điểm)
a) Tìm tất cả các số nguyên x, y thỏa mãn phương trình 2 2 2 2
x  xy  y  x y .
b) Với a, b là các số thực dương thỏa mãn ab  a  b  1. Chứng minh rằng: a b 1 ab   . 2 2 1 a 1 b 2 2 1 a  2 1 b  Câu 4. (3,5 điểm)
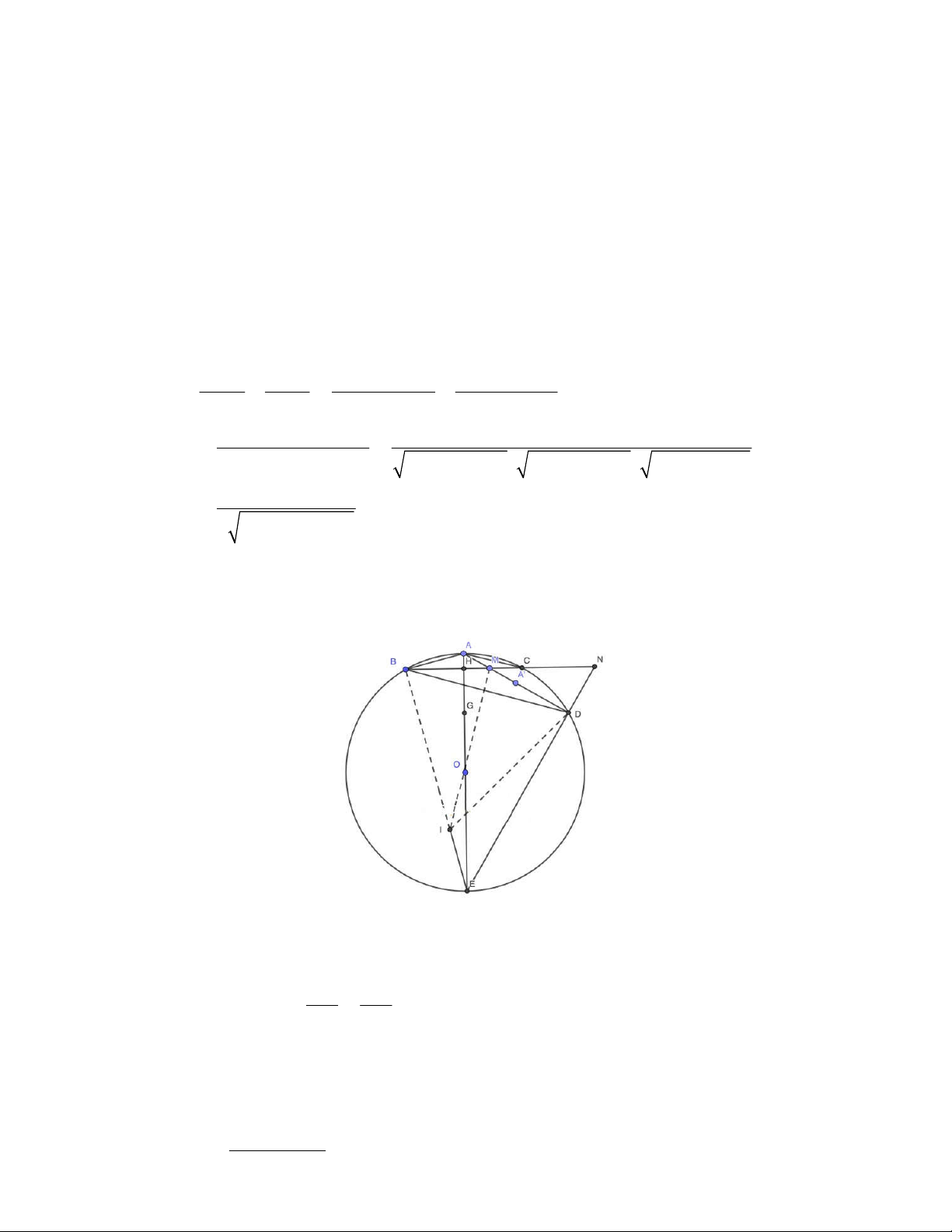
Cho tam giác ABC cân tại  A  0
BAC  90  nội tiếp đường tròn O bán kính R, M là điểm nằm trên cạnh
BC sao cho BM  CM . Gọi D là giao điểm của AM và đường tròn O với D  
A , H là trung điểm của
đoạn thẳng BC. Gọi E là điểm chính giữa cung lớn BC, ED cắt BC tại N.
a) Chứng minh rằng MA MD  MB MC và BN CM  BM CN.
b) Gọi I là tâm đường tròn ngoại tiếp tam giác B .
MD Chứng minh rằng ba điểm B, I , E thẳng hàng. c) Khi 2AB  ,
R xác định vị trí của M để 2MA  AD đạt giá trị nhỏ nhất.
------------------------------ HẾT ------------------------------
LỜI GIẢI CHI TIẾT Câu 1.
a) Điều kiện: x  2019. Nhân cả hai vế của phương trình cho
x  2020  x  2019, ta được:  2
4039 1 x  x  2019 2020  4039 x  2020  x2019
 x  2020  x2019 1 x  2020x2019    
x  2020x  2019  x  2020  
  x 2019   1  0  
  x2019  
1  x  2020   1  0  x2019 1    x  2020.   x  2020 1 
So với điều kiện ban đầu ta thấy x  2020 là nghiệm duy nhất của phương trình. 1 1 1 b) Ta có
   2m  n m . n m n 2
Phương trình tương đương: 2
x  mx  n  0   1 hoặc 2
x  nx  m  0 2. Phương trình  
1 và 2 lần lượt có 2
  m 4n và 2   n 4 . m 1 2
Ta có:     m  n  4m  4n  m  n  2mn  m  n2 2 2 2 2  0. 1 2
Suy ra một trong hai số  hoặc  lớn hơn hoặc bằng 0. 1 2
Do đó một trong hai phương trình  
1 hoặc 2 luôn có nghiệm.
Suy ra phương trình đã cho luôn có nghiệm. Câu 2. 2 2 Ta có: P   2 2
2 x  y  4x  y  xy 7  2x  y  4x  y 7  2x  y   1  5  5.
y  x 1
y  x 1  
Đẳng thức xảy ra khi và chỉ khi    1
  x  y  5 x     . 0; 4  
Chẳng hạn x  2; y  3 hoặc x  3; y  4.
Vậy giá trị nhỏ nhất của P là 5 đạt được khi y  x 1 và x  0; 4. Câu 3. a) Ta có 2 2 2 2
x y  x  xy  y  y  x . y Mặt khác 2 2 2 2
x y  x  xy  y  x  y . x
Suy ra: x  y hoặc x   . y
Với x  y, ta có: 2 4
3x  x  x  0  y  0. x  0 
Với x  y, ta có: 2 4
x  x   x  1 .  x  1 
Với x 1, ta có: y  1.  Với x  1  , ta có: y 1.
Vậy phương trình đã cho có ba nghiệm  ;
x y  0;0, 1;  1 , 1;  1 . b) Ta có: 2 2
ab  a  b  1  1 a  a  ab  a  b  a  ba   1 . Tương tự 2
1 b  a  bb   1 . Suy ra: a b a b    2 2 a 1 b 1
a ba   1
a bb   1
2ab  a  b 1 ab  
a b1 a1b
a b1 a a b1 a 1 a1b 1 ab  2  2 1 a  2 1 b 
Suy ra điều phải chứng minh. Câu 4.     
a) Ta có: ABM  MDC do cùng chắn cung AC và AMB  CM . D MA MB Suy ra BM  A  DMC  do đó:  . MC MD
 MA MD  MB MC.   ABE  và AC 
E có AE là cạnh chung, AB  AC và ABE  ACE nên ABE   AC  E.   ABE  ACE Suy ra   0 ABE  ACE 
 90 (do tứ giác ABEC nội tiếp). 2 
Suy ra AD là đường kính của O. Mà D O nên 0
ADE  90 hay MD  EN. NE NH Ta có NHE   NDM   
 NM  NH  NE  ND   3 . NM MD NC NE Lại có: NC  D  NE  B  
 NB NC  NE  ND 4. ND NB Từ  
3 và 4 suy ra NM  NH  NB  NC  MN  MC . NB
Suy ra: BN  MC  MN  NH  MN  NB  MN NH  NB  MN  BH.
Hay BN CM  MN  BH   5 .  
Tứ giác AHDN nội tiếp do có 0
AHN  NDA  90  MA MD  MH  MN.
Tứ giác ABDC nội tiếp  MA MD  MB MC.
Do đó: MH  MN  MB MC  MB MN CN .
Suy ra: BM CN  MN MB  MH   MN  BH 6. Từ  
5 và 6 suy ra: BN CM  BM CN. b) Ta có:      2  BDM MBD BID BIM MID   0 0 0 0   IBD  90   90   90 
 90 ADC CBD 0   90  . AED 2 2 2  0 
Suy ra: IBD  90  AE . D   0 
Mà EBD  EAD  90  AE . D Do đó  
IBD  EBD hay B, I , E thẳng hàng.   
c) Ta có: ABM  ACB  ADB nên AB  M   . ADB 2 AB AM R Suy ra: 2 
 AD AM  AB  . AD AB 4 2 R
Áp dụng bất đẳng thức AM – GM, ta có: 2AM  AD  2 2AM  AD  2 2  R 2. 4 2
Đẳng thức xảy ra khi và chỉ khi 2 AM  AD hay M là trung điểm .
AD Khi đó AD  . R 2
Vậy giá trị nhỏ nhất của của 2 AM  AD là R 2 đạt được khi M là trung điểm AD với D là điểm sao cho 2 AD  . R 2
------------------------------ HẾT ------------------------------