Đề thi vào lớp 10 môn Toán (chuyên) năm 2023 – 2024 sở GD&ĐT Lai Châu

TUYỂN TẬP ĐỀ THI CHÍNH THỨC VÀO 10 – NĂM 2023-2024 UBND TỈNH LAI CHÂU HƯỚNG DẪN CHẤM
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH VÀO LỚP 10 NĂM HỌC 2023-2024 Môn thi: Toán Câu Đáp án Điểm 1.a. 1,0
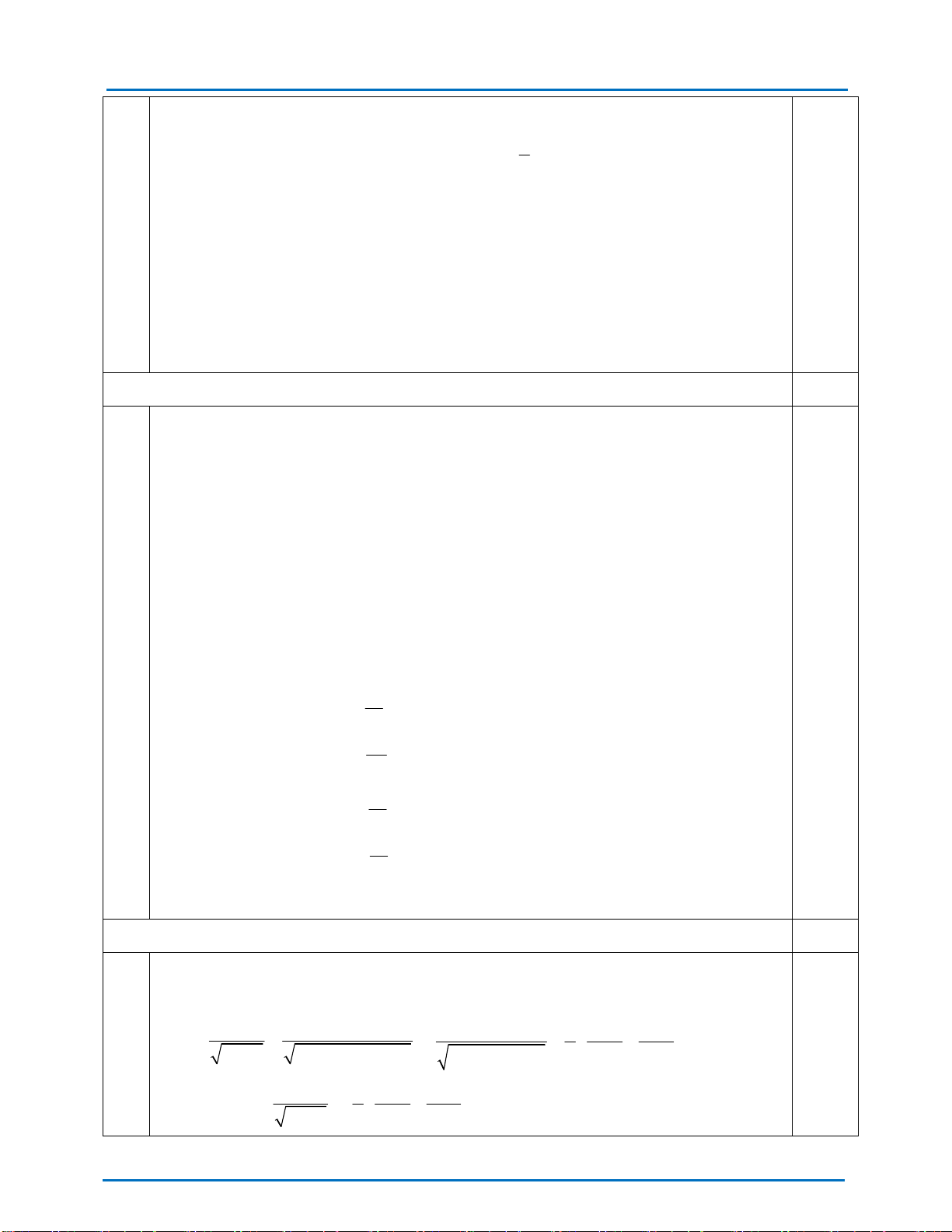
 x  4 x  4 x  x   1 1  A     :      x  x  2 1 
x   x 1 1 x   x x x   22  1    x 1 x 1    :
  x 2 x 1 1 x1 x    
 x  1 x  1      x  2 x  2 x     : x 1 1 
x   x   1  x   1
 x  1 x  1 2 x 1  .  x 1 2 x x x 1 Vậy A 
với x  0, x  1 x 1.b. 1,0 1 2023 A  2023 x 1 1 2023   x 2023 x 1 1 2023    0 x 2023
x. 2023  2023  x  x. 2023   0 x. 2023  2023  x  0  x  2023  x  2023  0  x  2023
Kết hợp với đk x  0, x  1 có 2022 giá trị thỏa mãn điều kiện 2. a. 1,0 CLB Toán THCS Trang 2
TUYỂN TẬP ĐỀ THI CHÍNH THỨC VÀO 10 – NĂM 2023-2024 2 2 
x  y  x  y  8 (1)  2 2
2x  y  3xy  3x  2 y 1  0 (2)  2 2
x  y  x  y  8 
 x y   
1 2x  y   1  0  2 2
x  y  x  y  8 
 x  y 1
 y  2x 1  2 2
x  y  x  y  8  (*) x  y 1    2 2
x  y  x  y  8  (**)
 y  2x 1  2 2
x  y  x  y  8 Giải (*)  x  y 1  x  1 x  y 1  x  y 1  x  y 1 y  2        y  2   y   2 2
1  y   y   2 1  y  8 2 y 8      x  3  y  2     y  2  2 2
x  y  x  y  8
Giải (**)  y  2x 1 
 y  2x 1   x   2x  2 2
1  x  2x   1  8 
 y  2x 1   2
5x  7x  2  8 
 y  2x 1   2
5x  7x  6  0   3  3 x 
 y  2x 1  x    5  5       11 3   x    y 2x 1    y      5 5   x  2    x  2     x  2 
 y  2x 1    y  3    3 11
Vậy hệ phương trình đã cho có 4 nghiệm 1; 2 ;  3  ;  2 ;  2  ;  3 ; ;    5 5  2. b. 1,0
Xét phương trình hoành độ giao điểm của  P và d  : 2
x  x  m 1 2
 x  x  m 1  0 * CLB Toán THCS Trang 3
TUYỂN TẬP ĐỀ THI CHÍNH THỨC VÀO 10 – NĂM 2023-2024
Để d  cắt  P tại 2 điểm phân biệt x ; x thì * có 2 nghiệm phân biệt 1 2 5
   0  1 4 m  
1  0  4m  5  0  m   4 Ta có: 2
x  x  4m 1  0 1 1 2  
Vì x là nghiệm của * 2
 x   x  m 1 thay vào   1 ta được 1 1 1
x  m 1 x  4m 1  0 1 2
   x  x  3m  2  0 1 2 
Theo Viet ta có: x  x  1  1 3m  2  0  m  1 (Nhận). 1 2 Vậy m  1 3. a. 1
a) 2x  y x  y  x  8y  22
 2x  y x  y  32x  y  5 x  y  22
 2x  y x  y  3  5 x  y  3  7
  x  y  32x  y  5  7
Khi đó ta có các khả năng sau:
x  y  3  7  x  2 KN1:   
2x  y  5  1   y  8 
x  y  3  1  x  2  KN2:   
2x  y  5  7 y  2    10 x 
x  y  3  7   3 KN3:    L
2x  y  5  1 2   y    3  10 x 
x  y  3  1   3 KN4:     L
2x  y  5  7 16   y    3
Vậy nghiệm nguyên của phương trình là  ; x y     2  ;8; 2  ; 2 3.b. 1
Ta có: a  b  c  3
 a  b  c2 2 3
 3ab  bc  ac  ab  bc  ac  3 bc bc bc 1  bc bc  Ta có:       2 2 a  3
a  ab  bc  ac
a  ba  c 2  a  b a  c  ac 1  ac ac  Tương tự ta có:     2 b  3 2  a  b b  c  CLB Toán THCS Trang 4
TUYỂN TẬP ĐỀ THI CHÍNH THỨC VÀO 10 – NĂM 2023-2024 ab 1  ab ab      2 c  3 2  b  c a  c 
Cộng vế với vế của các bất đẳng thức trên ta được: ab bc ac 1  bc bc ac ac ab ab            2 2 2 c  3 a  3 b  3 2  a  b a  c a  b b  c b  c a  c  ab bc ac 1  bc ac bc ab ac ab             2 2 2 c  3 a  3 b  3 2  a  b a  b a  c a  c b  c b  c  ab bc ac
1  c a  b
b a  c
a b  c          2 2 2 c  3 a  3 b  3 2 a  b a  c b  c   ab bc ac 1    
a  b  c 2 2 2 c  3 a  3 b  3 2 ab bc ac 3
Mà a  b  c  3 nên     2 2 2 c  3 a  3 b  3 2
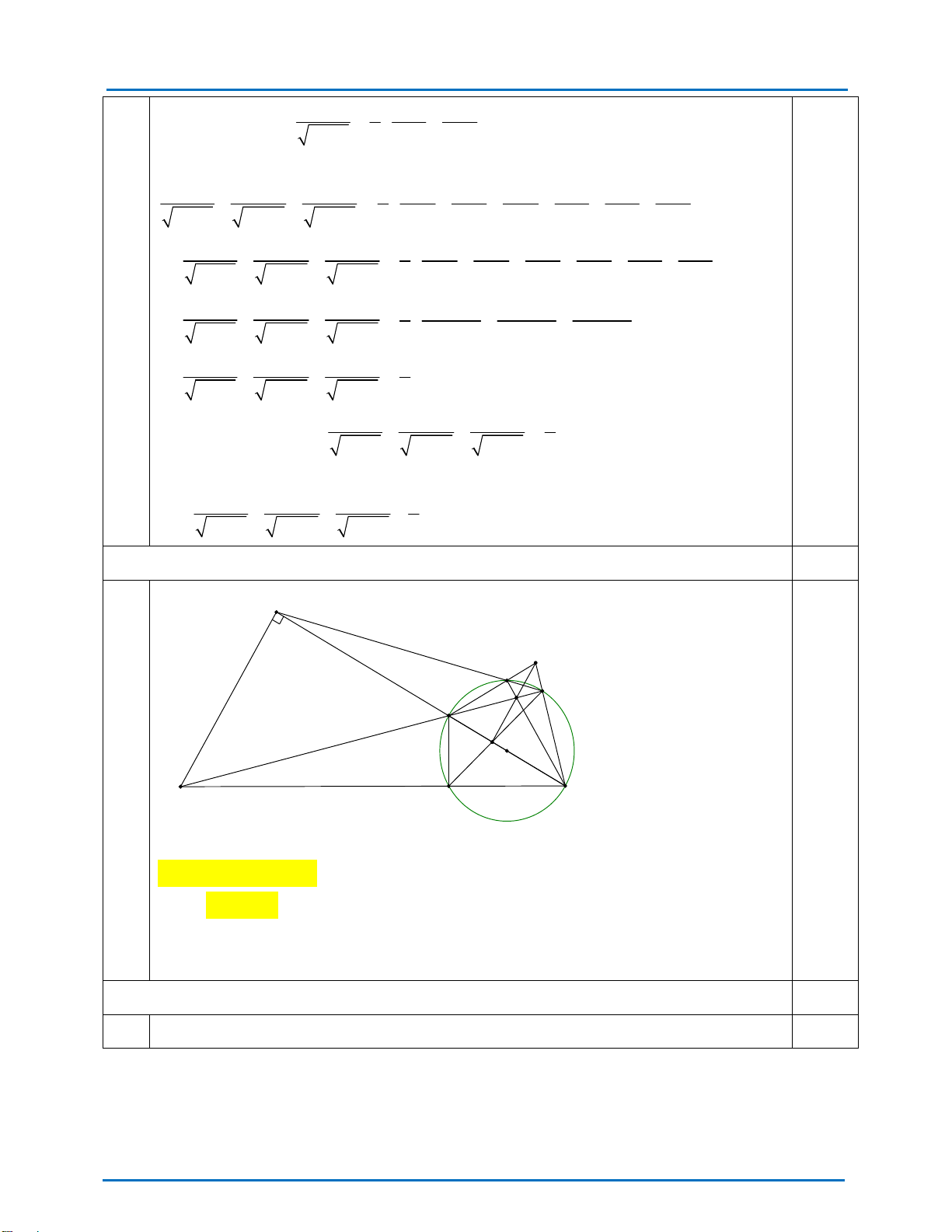
Dấu = xảy ra khi a  b  c  1 ab bc ac 3 Vậy    2 2 2 2 c  3 a  3 b  3 4.a. 1 A I G D F K H O B E C
a. Chứng minh rằng: ABEF là tứ giác nội tiếp. 
Tam giác ABC vuông tại A nên BAC  90 hay  BAF  90  
Ta có: FE  BC tại E nên FEB  FEC  90
Xét tứ giác ABEF có:  
BAF  FEB  180 mà hai góc đối nhau
Nên ABEF là tứ giác nội tiếp. 4.b. 1
b. Chứng minh: FH.CA  CH.FA CLB Toán THCS Trang 5
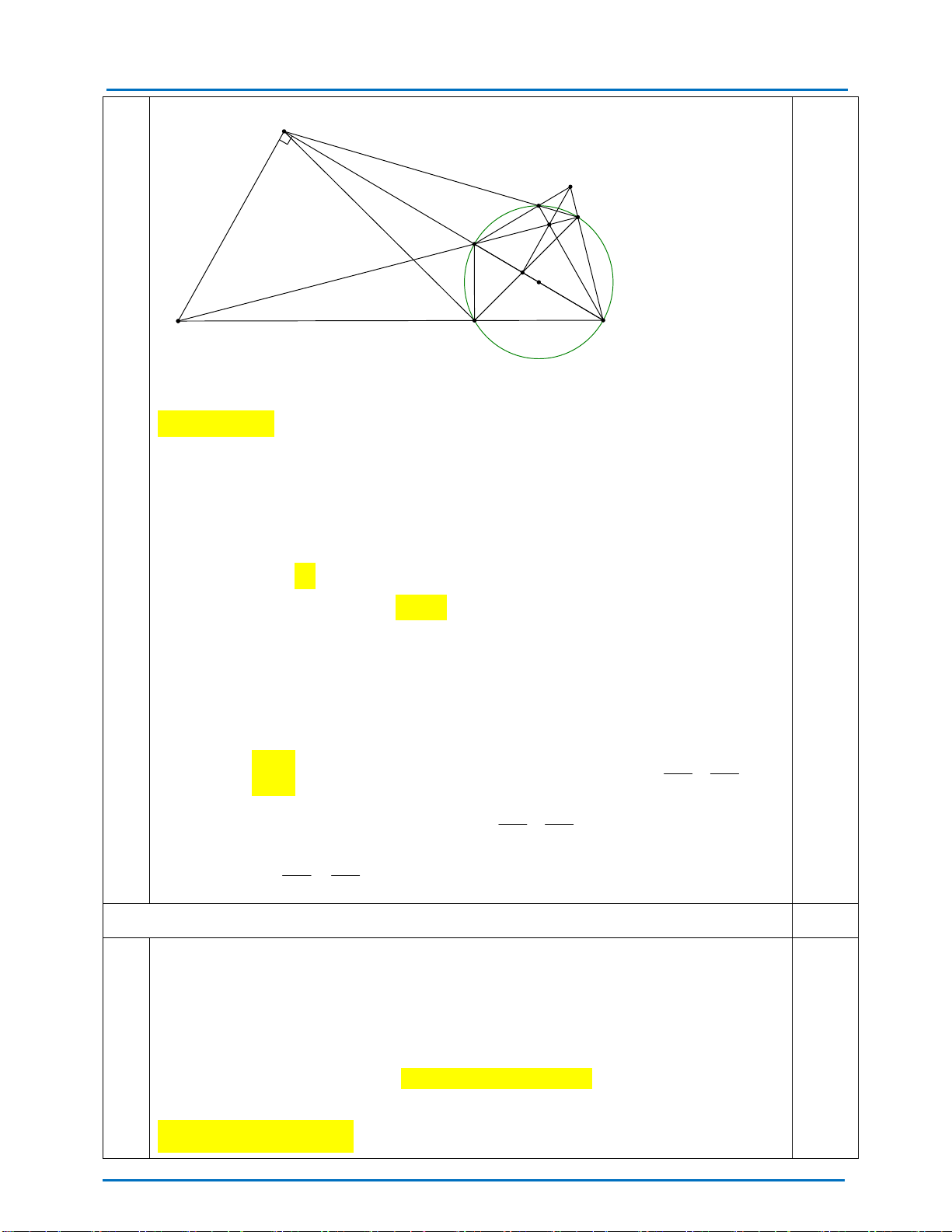
TUYỂN TẬP ĐỀ THI CHÍNH THỨC VÀO 10 – NĂM 2023-2024 A I G D F K H O B E C 
Xét đường tròn tâm O có FDC  90 (góc nội tiếp chắn nửa đường tròn) Hay  BDC  90  
Xét tứ giác ABCD có: BAC  BDC  90 mà hai đỉnh kề
Nên ABCD là tứ giác nội tiếp.  
Xét đường tròn ngoại tiếp tứ giác ABCD có ABD  ACD (hai góc nội tiếp cùng chắn  AD )  
Hay ABF  FCD (1)
Xét đường tròn ngoại tiếp tứ giác ABEF có  
ABF  AEF (hai góc nội tiếp cùng chắn  AF ) (2)  
Xét đường tròn tâm O có FED  FCD (hai góc nội tiếp cùng chắn cung  DF ) (3) Từ (1); (2); (3) ta có:  
AEF  FED nên FE 
là tia phân giác của AED AF AE
Xét tam giác AEH có EF là đường phân giác trong của tam giác nên  (4) FH EH AC AE
EC là đường phân giác ngoài của tam giác nên  (5) CH EH AF AC Từ (4); (5) ta có: 
 AF.CH  FH.AC FH CH 4.c. 1
Đường thẳng AD cắt O tại điểm thứ hai là G , FG cắt CD tại I , CG cắt FD tại K .
Chứng minh rằng K; I ; H thẳng hàng. 
Xét đường tròn tâm O có FGC  90 (góc nội tiếp chắn nửa đường tròn)  CG  FI
Xét tam giác IFC có ,
FD CG là hai đường cao mà FD cắt CG tại K
Nên K là trực tâm tam giác IFC  IK là đường cao IFC
Do đó IK  FC (6)   
Xét đường tròn tâm O có FDA  FCG (hai góc nội tiếp cùng chắn cung GF ) CLB Toán THCS Trang 6
TUYỂN TẬP ĐỀ THI CHÍNH THỨC VÀO 10 – NĂM 2023-2024  
Mà FDA  BCA (hai góc nội tiếp cùng chắn cung 
AB của đường tròn ngoại tiếp tứ giác ABCD )    
Do đó BCA  FCG Hay FCE  FCG     Xét F
 EC và FGC có; FCE  FCG ; FEC  FGC  90 Nên FEC  ∽   F
 GC  g.g   EFC  GFC  
Do đó  GC  EC  1   1 
Xét đường tròn tâm O có GFC  s®GC ; EDC  s®EC 2 2  
 GFC  EDC hay   IFH  HDC  
Xét tứ giác FHDI có: IFH  HDC mà góc ngoài bằng góc trong tại đỉnh đối
Nên FHDI là tứ giác nội tiếp.  
 FHI  FDI  90  IH  FC (7)
Từ (6) và(7 ) ta có K; I; H thẳng hàng. 5: 1
Gọi d là đường thẳng trong 2025 đường thẳng thỏa mãn đề bài, A E B d Q P I H F D G C
Giả sử d cắt AD và BC lần lượt tại P và Q và cắt EG tại I
E; F;G; H là trung điểm của các cạnh như hình 2 Mà S  2S
  DP  QC   2 AP  BQ  GI  2.IE  GI  GE  I cố DCQP ABQP 3 định
Khi đó ta có 2025  4.506 1các đường thẳng thỏa mãn đề bài phải đi qua 4 điểm cố định
Khi đó theo nguyên lý Dirichlet thì có 506 1  507 đường thẳng đi qua một điểm. CLB Toán THCS Trang 7
Document Outline

• de-thi-vao-lop-10-mon-toan-chuyen-nam-2023-2024-so-gddt-lai-chau
• Đề Chuyên Lai Châu 23 - 24