Đề thi vào lớp 10 môn Toán năm 2020 – 2021 trường chuyên Lê Quý Đôn – Đà Nẵng

SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT CHUYÊN LÊ QUÝ ĐÔN
THÀNH PHỐ ĐÀ NẴNG
NĂM HỌC 2020 – 2021 ------------------ Môn: TOÁN (chuyên)
Thời gian làm bài: 150 phút (không kể thời gian phát đề) Câu 1. (2,0 điểm)
a) Chứng minh rằng với mọi giá trị dương, khác 1 của x thì biểu thức A không nhận giá trị nguyên, với:     x 1  x 1 1 x  3 A           x 1 x 1 4 x 4  x  2 x  9 2 2 2 2 2 2
x  y  z x y z b) Xét các bộ  ;
x y; z thỏa mãn   
với a, b, c là các số thực khác 0. 2 2 2 2 2 2
a  b  c a b c 2020 2020 2020 x y z
Tính giá trị của biểu thức: Q    . 2 2 2 2 2 2 b c c a a b
Câu 2. (1,0 điểm) Trên đồ thị hàm số 2
y  0,5x , cho điểm M có hoành độ dương và điểm N có hoành độ
âm. Đường thẳng MN cắt trục Oy tại C với O là gốc tọa độ. Viết phương trình đường thẳng OM khi C là
tâm đường tròn ngoại tiếp tam giác OMN. Câu 3. (2,0 điểm) a) Giải phương trình: 3 2
x  x  x   3 x   3 3 2 28 4 x 7  0. 2 3
 x  4xy x  3yy   3 
b) Giải hệ phương trình:  . 8 2 2
 x 6y 1 y 2x9   3
Câu 4. (1,0 điểm) Tìm tất cả các giá trị của m để phương trình:  2 2
x  x  m  m   2 2 2 2
15 2x  3x  m  2m   14  0
có bốn nghiệm phân biệt x , x , x , x thỏa mãn 2 2 2 2
x  x  x  x  3x x . 1 2 3 4 1 2 3 4 2 3  
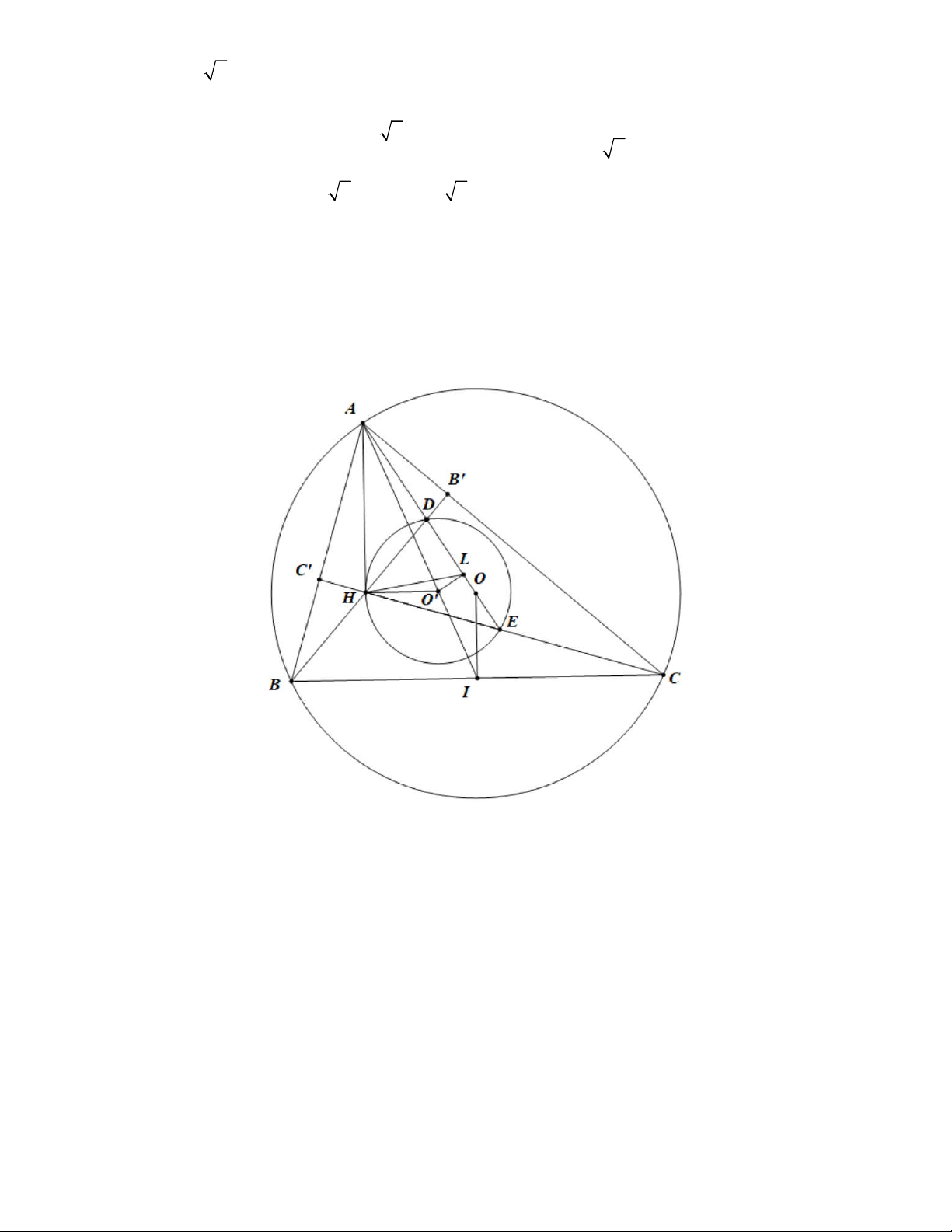
Câu 7. (2,0 điểm) Cho tam giác ABC nhọn B  C, nội tiếp đường tròn tâm .
O Các đường cao xuất phát từ
B và C lần lượt cắt đường thẳng AO lần lượt tại D và E. Gọi H là trực tâm giác ABC và O là tâm đường
tròn ngoại tiếp tam giác HDE. Chứng minh rằng:
a) Tam giác HDE đồng dạng với tam giác ABC và AH là tiếp tuyến của O.
b) Đường thẳng AO đi qua trung điểm của đoạn BC.
Câu 6. (1,0 điểm) Cho tam giác ABC nhọn  AB  AC, nội tiếp đường tròn tâm .
O Kẻ đường phân giác AD,
D  BC của tam giác đó. Lấy điểm E đối xứng với D qua trung điểm của đoạn BC. Đường thẳng vuông góc
với BC tại D cắt AO ở H , đường thẳng vuông góc với BC tại E cắt ở AD tại K. Chứng minh rằng tứ giác BHCK nội tiếp.
Câu 7. (1,0 điểm) Cho các số thực dương x, y, z thỏa mãn x  y  z  3. Chứng minh rằng: 2 2 2 2 2 2   x  y y  z z  x  x  y y  z z  x           
xyx  y
yz y  z
zxz  x 3 2 .  xy yz zx 
---------------------- HẾT ----------------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT CHUYÊN LÊ QUÝ ĐÔN
THÀNH PHỐ ĐÀ NẴNG
NĂM HỌC 2020 – 2021 ------------------ Môn: TOÁN (chuyên)
Thời gian làm bài: 150 phút (không kể thời gian phát đề) Câu 1.
a) Với x  0 và x 1, ta có:     x 1  x 1 1 x  3 A           x 1 x 1   4 x 4  x  2 x  9    x  2 1  x  2 1  1 x 1         s x   1  x  
1 4 x x2 x 9    4 x 1 x 1 1    1 . x 1  4 x x  2 x  9 x  2 x  9 1 Vậy A  1 . x  2 x  9
Nếu A   thì 1 
 x 2 x   9 mà: x 
x    x  2 2 9
1  8 1 nên A không thể là số nguyên. 2 2 2 2 x x y y 2 2 z z b) Ta có:  ,  và  . 2 2 2 2 2 2 2 2 a
a  b  c b
a  b  c 2 2 2 2 c
a  b  c 2 2 2 2 2 2 2 2 2 x y z x y z
x  y  z Từ đó suy ra:       . 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 a b c
a  b  c
a  b  c
a  b  c
a  b  c
Do đó đẳng thức xảy ra khi và chỉ khi x  y  z  0. Từ đó Q  0. Câu 2. Ta gọi: M  2 m  m  N  2 ; 0, 5 , ;
n 0,5n , C x ; y trong đó m  0. C C 
Do C là tâm đường tròn ngoại tiếp tam giác OMN mà C  MN nên tam giác OMN vuông tại O và C là  m  n x   C  2
trung điểm MN. Khi đó  . 2 2  0,5m 0,5n y  C  2 2  m    2 m
Ta có: C  Oy nên x  0 suy ra m   .
n Khi đó C 0; . Suy ra: OC  , OM  . m C    2  2
Mặt khác C là tâm đường tròn ngoại tiếp tam giác OMN nên: 2 m OC  OM 
 m  m  2 do m  0. 2 Suy ra M 2; 2
 . Phương trình đường thẳng OM có dạng y  ax mà đi qua điểm M 2;  2 nên a  1. 
Vậy y  x là đường thẳng cần tìm. Câu 3. a) Điều kiện: 3
x  7. Ta có phương trình tương đương: 2
x x   3 x  x   3x   3 1 2 2 28 4 x  7  0
Nhận xét x  2 là một nghiệm của phương trình.
Nếu x  2, ta có: 2
x x   3 x  x   3x   3 1 2 2 28 4 x 7  0.
Nếu 3 7  x  2, ta có: 2
x x   3 x  x   3x   3 1 2 2 28 4 x 7  0.
Vậy phương trình đã cho có nghiệm duy nhất x  2. 2
x 6y 1 0  b) Điều kiện 
. Phương trình thứ nhất của hệ tương đương: 2
y 2x9 0  2 2
x  4xy  3y 3x 3y  0
 x3yx  y3x 3y 0
 x3yx  y   3  0 x  3y   . x  y 3  
Với x  3y, thay vào phương trình thứ hai của hệ ta được: 8 2 2
9 y 6 y 1 
y  6 y  9  3 8  3y 1   y 3  3 8
Nếu y  3 thì 3y 1  y 3  8  . 3 1 8 1 Nếu y 
thì phương trình tương đương: 13y  3 y 
 y   x 1. 3 3 3 1 8 1 1
Nếu  y  3 thì phương trình tương đương: 3y 1 3 y 
 y  không thỏa do  y  3. 3 3 3 3 
Với x  y  3, thay vào phương trình thứ hai của hệ ta được: y  2 8 2 3 6 y 1 
y  2 y   3  9  3 8 2 2
 y 10  y 2y 3  3
 y 10  y  2 8 2 1  2  3 8 Ta có
y 10   y  2 2
1  2  10  2  31 4 
nên phương trình này vô nghiệm. 3  
Vậy hệ cho có nghiệm duy nhất x y 1 ;  1  ; .    3 Câu 4. 2 2
2x  xm  2m15  0   1 
Phương trình tương đương: .  2 2
2x 3x m  2m 14   0 2  Phương trình  
1 có ac   m 
 m   m 2 2 2 2 15 2
1  28  0 nên có hai nghiệm phân biệt trái dấu.
Tương tự phương trình 2 cũng có hai nghiệm phân biệt trái dấu. Mà 2 2 2 2
3x x  x  x  x  x  0 nên x và x cùng dấu. Không mất tính tổng quát, giả sử x , x là nghiệm 2 3 1 2 3 4 2 3 1 2 của phương trình  
1 và x , x là nghiệm của phương trình 2. 3 4  1    3 x  x   
x  x   1 2    2 3 4  2
Theo định lý Viete, ta có:  và  . 2  m  2m 15  2     m 2m 14  x x   x x   1 2  2 3 4  2 Khi đó
x  x  x  x  x  x 2 x  x 2 2 2 2 2 2x x 2x x 1 2 3 4 1 2 3 4 1 2 3 4 2 2 2 2  1  3
 m 2m15
 m 2m14                2    2                  2 2  2   2     2 2 8m 16  m m m   121  5 63 8 16 126 2  2m 4m    2 4 4 a  5   2 a  8m 16  m   121 . 4
Chú ý rằng phương trình  
1 và phương trình 2 có cùng:      2 m 
 m     2 m   m  2 1 4 2 2 15 9 4 2 2
14  8m 16m 121 a 1. 1 a 1   a Phương trình  
1 có hai nghiệm x  hoặc x  . 4 4 3 a 3 a
Phương trình 2 có hai nghiệm x  , x  . 4 4 1 a 1 a 3 a 3 a
Xét trường hợp x  , x  , x  , x  . 1 2 3 4 4 4 4 4 a  4 a  3 Ta có: x x 
. Yêu cầu bài toán tương đương: 2 3 16 3a 4 a a   3 5   4a  
5 3a 4 a   3  0 4 16
 a 12 a 11 0
Phương trình này vô nghiệm. 1 a 1 a 3 a 3 a
Xét trường hơp x  , x  , x  , x  . 1 2 3 4 4 4 4 4 a  4 a  3 Ta có: x x 
. Yêu cầu bài toán tương đương: 2 3 4 3a  4 a a   3 5   4a  
5 3a  4 a   3  0 4 16
 a 12 a 11 0  a 11 a   1  a 121. m  0
Với a  121, ta có: 2 2 8m 16
 m 121121  m 2m  0   .  m  2 
Vậy m  0 hoặc m  2 là các trị cần tìm. Câu 5.
a) Gọi BB và CC là đường cao của tam giác ABC.    Tứ giác AC HB   nội tiếp nên  C HB   C AB 
  BAC do cùng bù với góc C HB  .     Mà  C HB 
 DHE nên DHE  BAC   1 .  AOC
Tam giác OAC cân tại O nên  0 0   OAC  90 
 90  ABC  BAH. 2   Mặt khác C  AE 
vuông tại C nên 0 C AE 
 AEC  90 hay   0
DEH  BAE  90 .  0  0  
Suy ra DEH  90  BAE  90 BAH  HAE  
 90OAC  HAE 0    90  HAC  . ACB  
Do đó DEH  ACB 2. Từ  
1 và 2 suy ra tam giác HDE đồng dạng với tam giác ABC. Ta có   0  
DEH  ACB  90  HAC  AHB nên HA là tiếp tuyến của O.
b) Gọi I , L lần lượt là trung điểm của BC và DE. Mà tam giác HDE đồng dạng với tam giác ABC mà O là
tâm đường tròn ngoại tiếp tam giác HDE, O là tâm đường tròn ngoại tiếp tam giác ABC nên hai tam giác LHO  
và IAO đồng dạng với nhau nên LHO  IAO   3 .     Ta có O L
  DE và AH  HO nên tứ giác AHO L
 nội tiếp  LHO  LAO hay LHO  O AO    4 . Từ   3 và 4 suy ra:   IAO  O A  O hay ,
A O, I thẳng hàng.
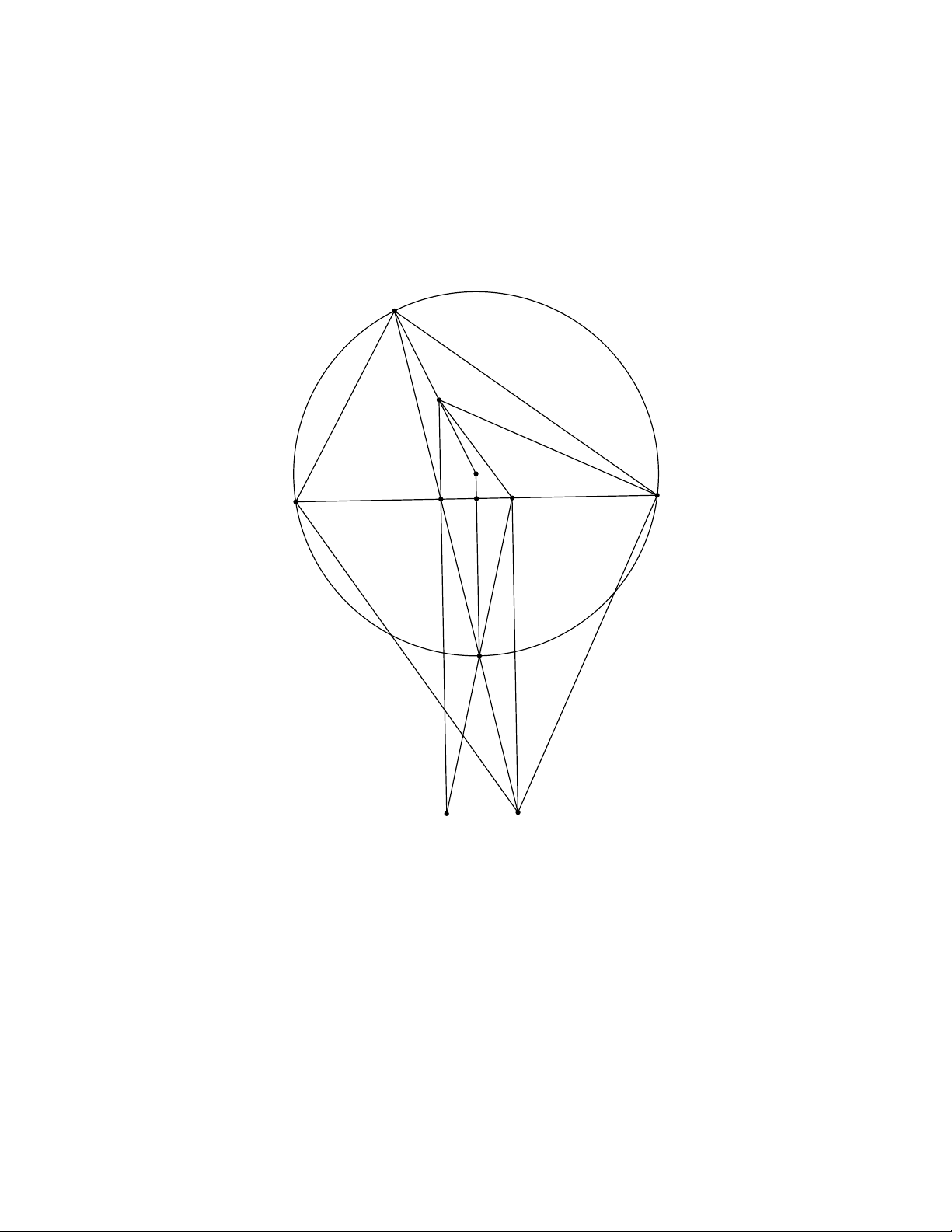
Do đó AO đi qua trung điểm của BC. Câu 6. A H O E C B D M P X K
Gọi P là giao điểm của AD và O thì P là điểm chính giữa cung BC, X là giao điểm của EP và DH.
Ta có OP là trung trực của DE nên OP  DH dẫn đến   
DAH  APO  ADH do đó AHD  cân tại H.
Do M là trung điểm của DE mà MP  EK  DX nên P là trung điểm của DK và EX .
Nên DEKX là hình bình hành, suy ra   BD  X  CEK 
 XBD  KCE. Mà  0
DEX  90 nên DP  DX  DE.
Ta có: XK  BC nên BKXC là hình thang cân nội tiếp đường tròn (1).
Ngoài ra tứ giác AHPX nội tiếp do  
AHD  APX  DH  DX  DA . DP
Mặt khác tứ giác ABPC nội tiếp nên DA DP  DB DC.
Suy ra DH  DX  DB  DC hay BHCX nội tiếp (2).
Từ (1) và (2) suy ra BHCK là tứ giác nội tiếp. Câu 7.
Áp dụng bất đẳng thức Cauchy – Schwars, ta có:   x  y 2  x  y 2  x  y2 2 2 2 2 2 2x  y         
xyx  y 2 x  y
 xyx  y x  y
xyx  y xy
Viết hai bất đẳng thức tương tự rồi công lai theo vế ta được: 2 2 x  y 2 x  y     
xy x  y 2 x  y xy
Do đó ta chỉ cần chứng minh bất đẳng thức sau là bài toán hoàn tất. 2 2 2    3 x  y y  z z  x 2 4 4 Thật vậy, ta có:   . x  y 2 2x  y 2  x  y 2  1 1 1  49 49   Do đó:   4        x  y
 x  y  y  z 
z  x  
x  y  z 3. 2 2 2 2  6 23 6
Đẳng thức xảy ra khi và chỉ khi x  y  z  1.
Vậy ta có điều phải chứng minh.
---------------------- HẾT ----------------------