SỞ GIÁO DỤC VÀ ĐÀO TẠO KÌ THI VÀO LỚP 10 THPT NĂM HỌC 2018-2019 BÌNH PHƯỚC
ĐỀ THI MÔN TOÁN (CHUNG) ĐỀ CHÍNH THỨC
Thời gian 120 phút (không kể thời gian phát đề)
(Đề gồm 01 trang) Ngày thi 01/06/2018 Câu 1 (2,0 điểm):
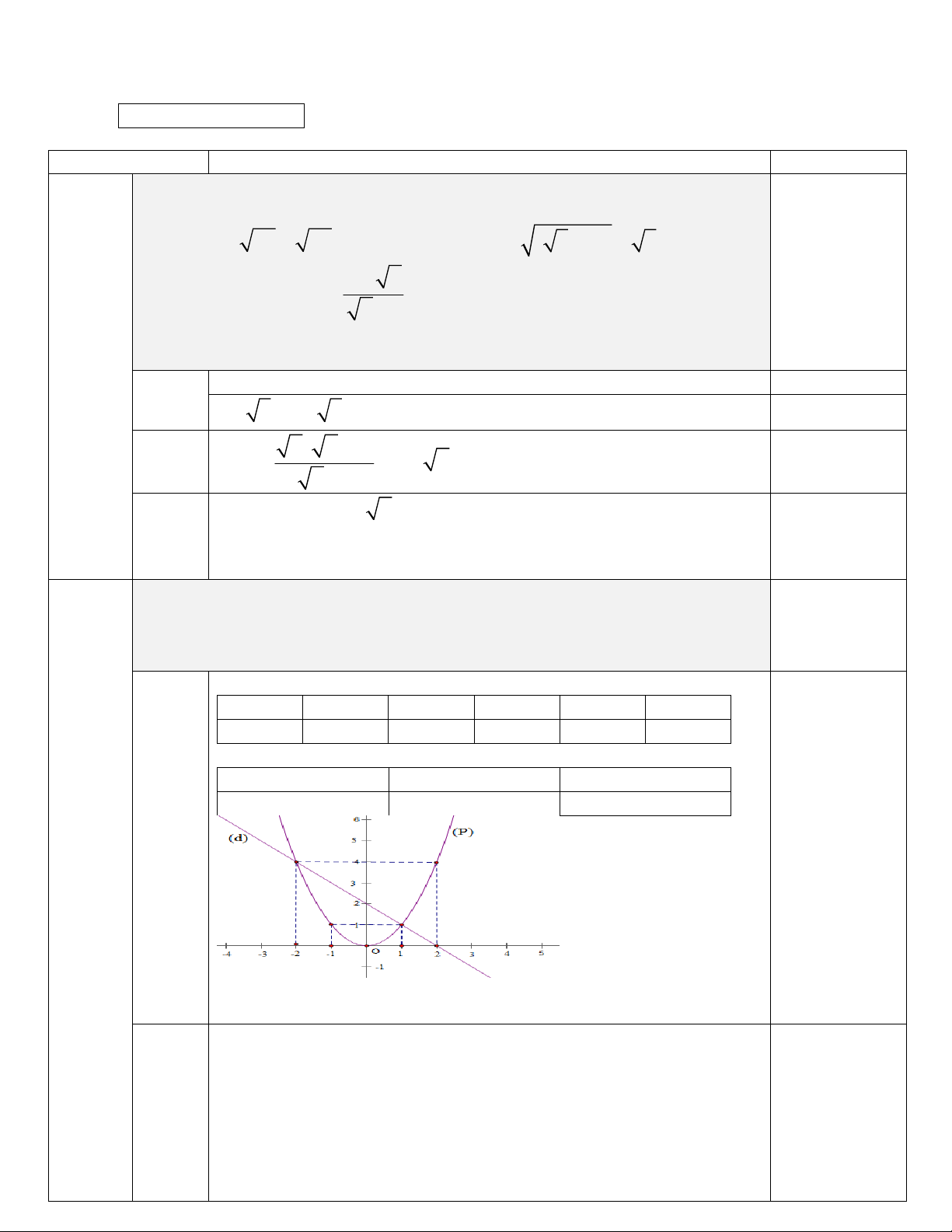
1. Tính giá trị của các biểu thức: M  36  25 2 N  ( 5 1)  5 x  x
2. Cho biểu thức P  1 , với x  0 à v x 1 x 1
a) Rút gọn biểu thức P .
b) Tìm giá trị của x , biết P  3 Câu 2 (2,0 điểm): 1. Cho parabol 2
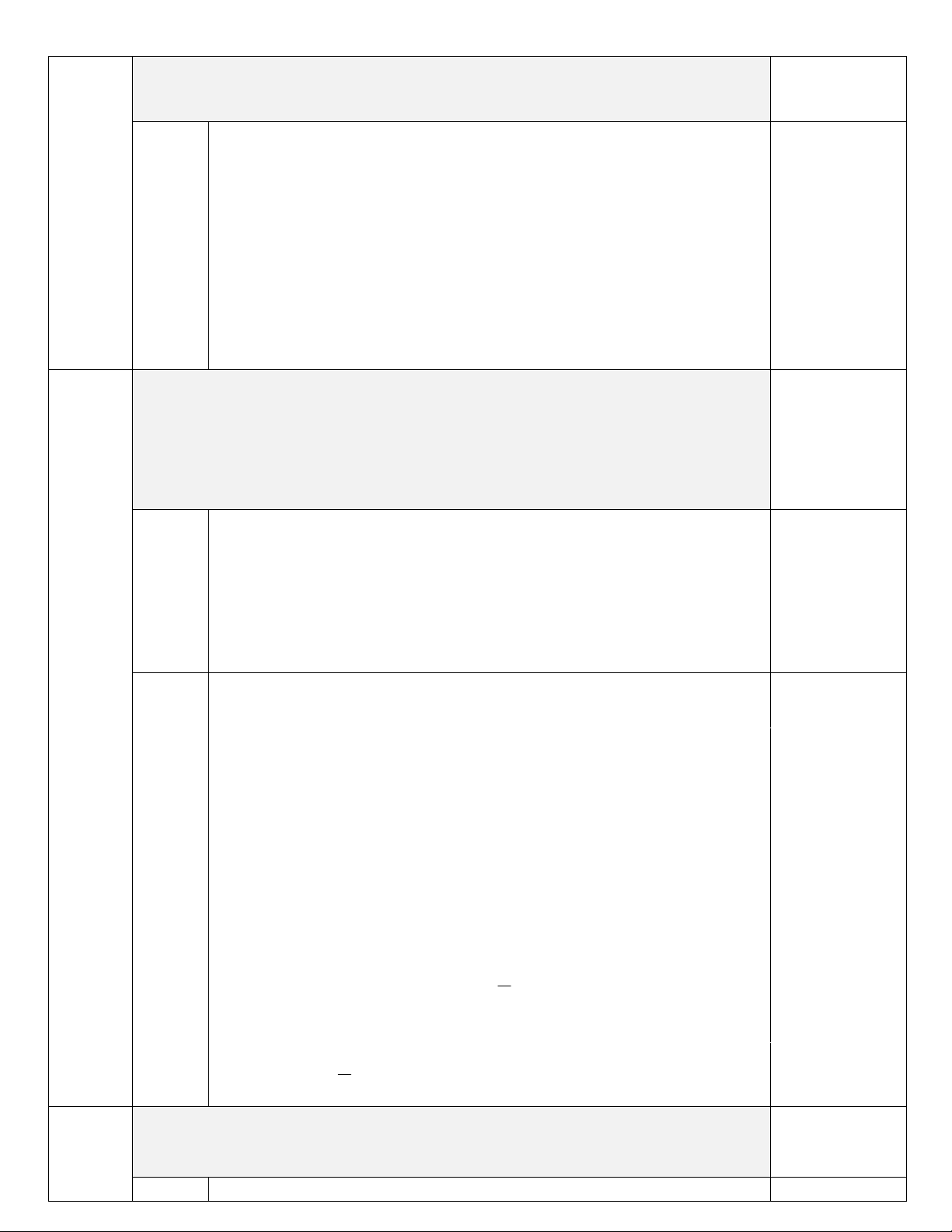
(P) : y  x   
và đường thẳng (d) : y x 2
a) Vẽ parabol (P) và đường thẳng (d ) trên cùng một mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm của parabol (P) và đường thẳng (d ) bằng phép tính. 3
 x  y  5
2. Không sử dụng máy tính, giải hệ phương trình sau: 
2x  y 10 Câu 3 (2,5 điểm): 1. Cho phương trình: 2
x  2mx  2m 1  0 ( m là tham số ) (1)
a) Giải phương trình (1) với m = 2.
b) Tìm m để phương trình (1) có hai nghiệm x , x sao cho: 1 2  2
x  2mx  3 2
x  2mx  2  50 1 1 2 2 
2. Quãng đường AB dài 50 km. Hai xe máy khởi hành cùng một lúc từ A đến B.
Vận tốc xe thứ nhất lớn hơn vận tốc xe thứ hai 10 km/h, nên xe thứ nhất đến B trước
xe thứ hai 15 phút. Tính vận tốc của mỗi xe. Câu 4 (1,0 điểm):
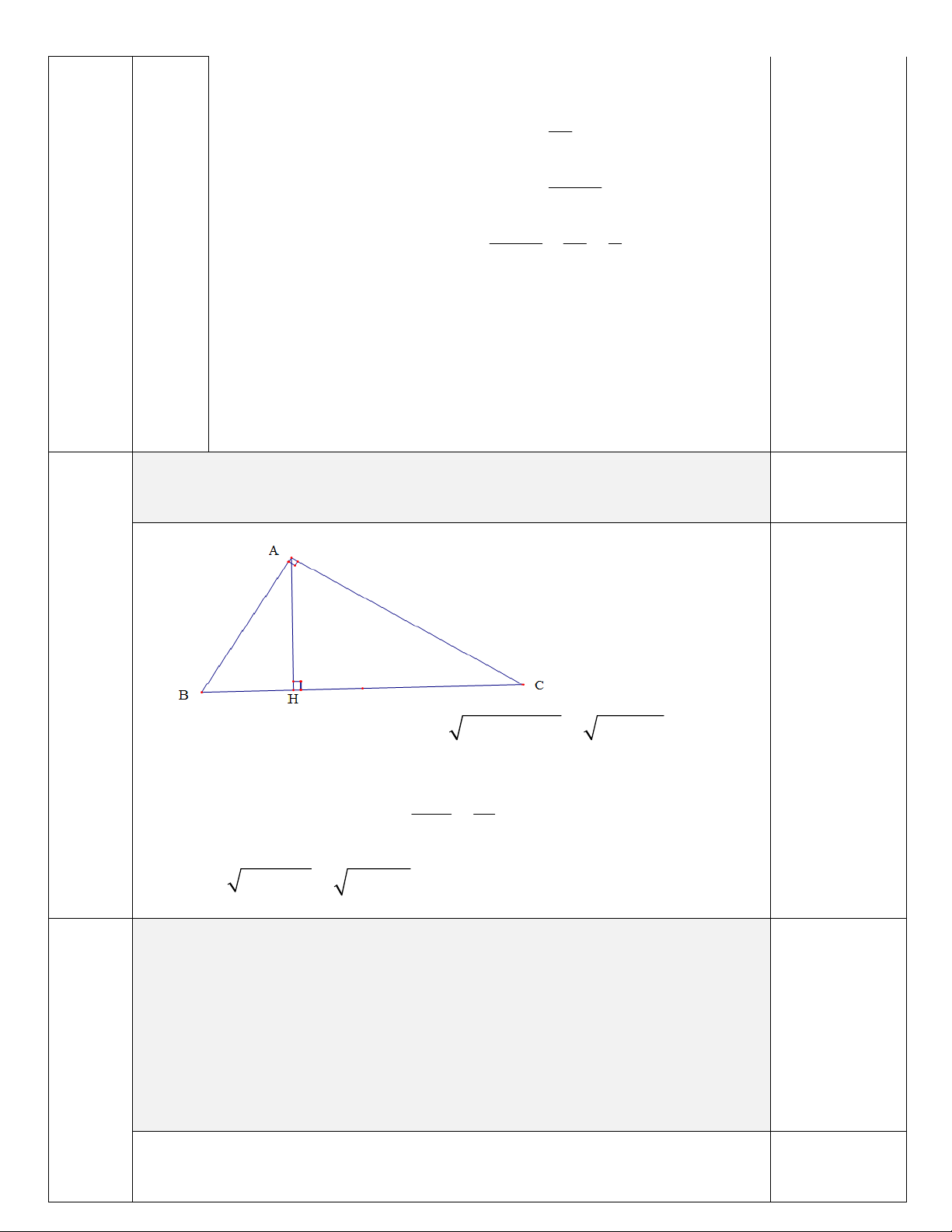
Cho tam giác ABC vuông tại A, đường cao AH H  BC . Biết
AC  8cm, BC  10cm . Tính độ dài các đoạn thẳng AB, BH , CH và AH. Câu 5 (2,5 điểm):
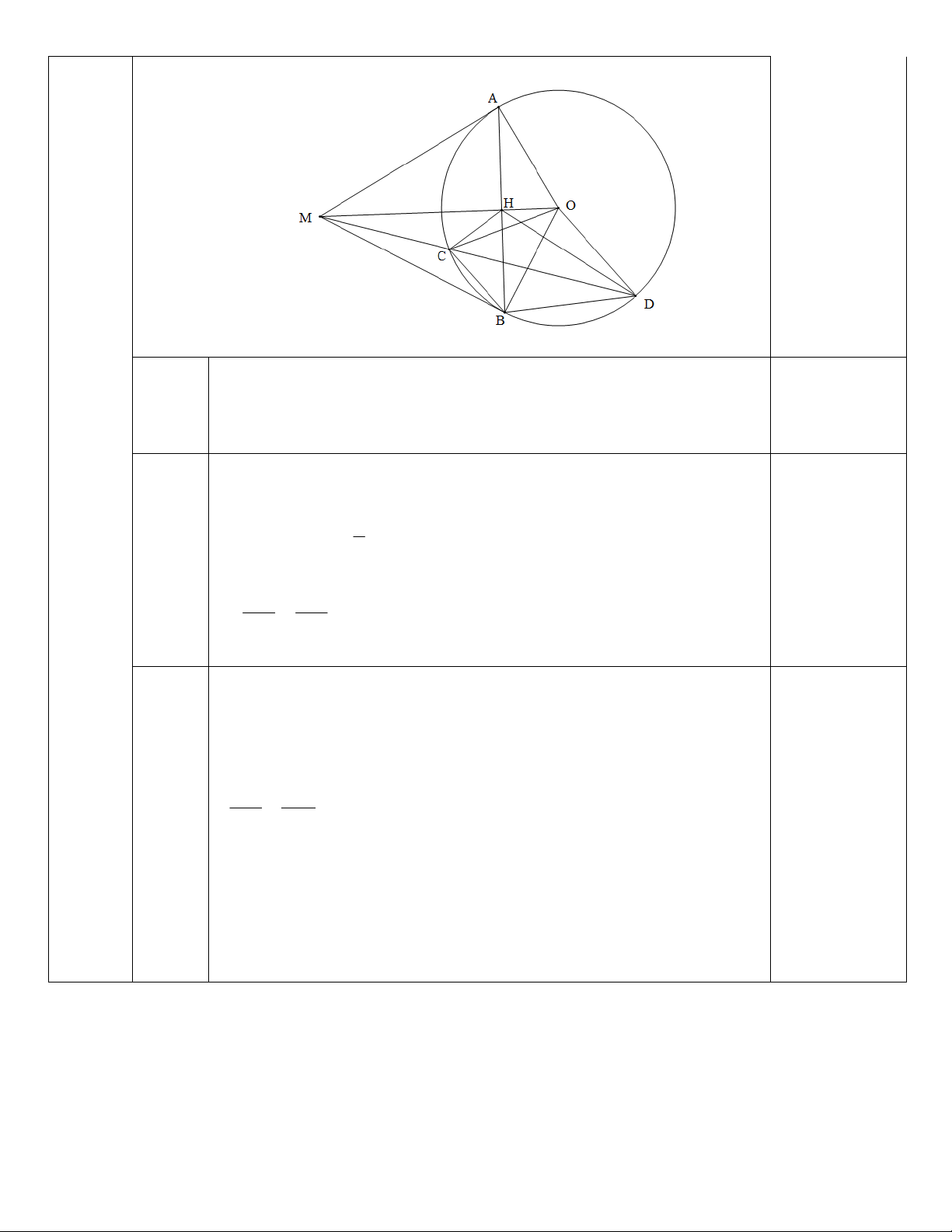
Cho đường tròn tâm (O), từ điểm M ở bên ngoài đường tròn (O) kẻ các tiếp tuyến MA,
MB (A, B là các tiếp điểm), kẻ cát tuyến MCD không đi qua tâm O (C nằm giữa M và
D; O và B nằm về hai phía so với cát tuyến MCD).
a) Chứng minh: tứ giác MAOB nội tiếp. b) Chứng minh: 2
MB  MC.MD
c) Gọi H là giao điểm của AB và OM. Chứng minh: AB là phân giác của  CHD Hết.
Chú ý: Thí sinh không được sử dụng tài liệu, cán bộ coi thi không giải thích gì thêm
Họ tên thí sinh:……………………………………………….SBD…………………
Họ tên, chữ ký giám thị 1:…………………………………………….......................
Họ tên, chữ ký giám thị 2:…………………………………………….......................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI VÀO LỚP 10 THPT NĂM HỌC 2018-2019 BÌNH PHƯỚC
HƯỚNG DẪN CHẤM MÔN TOÁN (CHUNG) ĐỀ CHÍNH THỨC Ngày thi 01/06/2018 Câu Nội dung Điểm Câu 1 (2,0 điểm)
1. Tính giá trị của các biểu thức: M = 36  25 ; N = 2 ( 5 1)  5 x  x 2. Cho biểu thức P = 1 , với x  0 à v x 1 x 1 Câu 1
a) Rút gọn biểu thức P. (2,0
b) Tìm giá trị của x, biết P >3 điểm) 1. M= 6+5 =11 0,25đ+0,25đ ( 1 đ) N= 5 1 5  1  0,25đ+0,25đ 2.a) x( x 1) 1 1 x (0,5 đ) P = 0,25đ+0,25đ x 1
P  3  1  x  3 0,125+0,125đ 2.b)
 x  4 thỏa mãn 0,125đ
(0,5đ) Vậy x  4 thì P > 3 0,125đ Câu 2 (2,0 điểm):
1. Cho parabol (P): y = x2 và đường thẳng (d) : y = - x + 2.
a) Vẽ parabol (P) và đường thẳng (d) trên cùng một mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm của parabol (P) và đường thẳng (d) bằng phép tính. Bảng giá trị x -2 -1 0 1 2 y = x2 4 1 0 1 4 0,125 đ x 0 2 0,125 đ 1a) y = - x + 2 2 0 (0,75 Câu 2 đ) ( 2,0 điểm) 0,25đ + 0,25đ
Ghi chú: Nếu HS không lập bảng giá trị mà chỉ biểu diễn điểm
rồi vẽ đúng vẫn cho điểm tối đa 0,75đ
Phương trình hoành độ giao điểm của (P) và (d): 2 2 x = -x + 2  x + x - 2 = 0 0,125 đ 1b)
 x+2x   1  0 0,125 đ (0,5 đ) x  2   y  4  
x 1 y 1 0,125 đ
Vậy tọa độ giao điểm của (P) và (d) là ( -2; 4), ( 1; 1) 0,125 đ 3
 x  y  5
2. Không sử dụng máy tính giải hệ phương trình sau: 
2x  y 10 5  x 15   0,25 đ
 y  5  3x x  3   (0,75 0,25 đ  y  5  3.3 đ) x  3  y  4 0,25 đ
Vậy nghiệm (x; y) của hệ là (3 ; - 4) Câu 3 (2,5 điểm): 1. Cho phương trình: 2
x  2mx  2m 1  0 (m là tham số) (1)
a) Giải phương trình (1) với m = 2.
b) Tìm m để phương trình (1) có hai nghiệm x , x sao cho: 1 2  2
x  2mx  3 2
x  2mx  2  50 1 1 2 2 
a) Thay m = 2 ta có phương trình x2 – 4x + 3 = 0 0,125 đ  ( x – 1 )( x – 3) = 0 0,125 đ 1a. (0,5 đ) x 1   0,25 đ x  3
Vậy tập nghiệm của phương trình là S = {1;3} 2 2
 '  m  2m  1  (m 1)  0 0,125 đ
 Phương trình (1) luôn có hai nghiệm x 0,125 đ 1, x2 với mọi m
Vì x1, x2 là là hai nghiệm của phương trình (1) nên ta có: 2
x  2mx  3  4  2m 1 1 0,125 đ 2
x  2mx  2  1   2m 2 2 0,125 đ Theo đề bài  2
x  2mx  3 2
x  2mx  2  50 1 1 2 2  Câu 3
 4  2m1 2m (2,5  1b. 50 0,125 đ điểm): (1đ) 2
 4m  6m  54  0 0,125 đ m  3  
m 32m 9 0       9 m  0,25 đ  2  9  Vậy m   3; 
 thỏa điều kiện đề bài 0,125 đ  2
2. Quãng đường AB dài 50 km. Hai xe máy khởi hành cùng một lúc từ A
đến B. Vận tốc xe thứ nhất lớn hơn vận tốc xe thứ hai 10km/h, nên xe thứ
nhất đến B trước xe thứ hai 15 phút. Tính vận tốc của mỗi xe.
Gọi vận tốc xe thứ nhất là x km/h ( x >10) 0,125 đ
Thì vận tốc xe thứ hai là x - 10 km/h 50 0,125 đ
Thời gian xe thứ nhất đi từ A đến B là h x 50 0,125 đ
Thời gian xe thứ hai đi từ A đến B là h x 10 (1 đ) 50 50 1
Theo đề bài ta có phương trình   0,125 đ x 10 x 4 2
 x 10x  2000  0 0,125 đ
 (x  50)(x  40)  0 0,125 đ x  50 (N)   0,125 đ
x  40 (L)
Vậy vận tốc xe thứ nhất là 50 km/h; vận tốc xe thứ hai là 40 km/h 0,125 đ Câu 4 (1,0 điểm):
Cho tam giác ABC vuông tại A, đường cao AH ( HBC ). Biết AC = 8cm,
BC = 10 cm. Tính độ dài các đoạn thẳng AB, BH, CH và AH . Câu 4 (1,0
Theo định lí Py-ta-go ta có 2 2 2 2
AB  BC  AC  10  8  6(cm) 0,25 đ điểm):  0 A  BC ó
c A  90 ; AH  BC 2 2 AB 6 0,25 đ 2
 AB  BH.BC  BH    3,6(cm) BC 10 0,25 đ
CH = BC – BH = 10 – 3,6 = 6,4 ( cm)
AH = BH.CH  3,6.6,4  4,8(c ) m 0,25 đ Câu 5 (2,5 điểm):
Cho đường tròn tâm (O), từ điểm M ở bên ngoài đường tròn (O) kẻ các tiếp
tuyến MA, MB (A, B là các tiếp điểm), kẻ cát tuyến MCD không đi qua tâm
O (C nằm giữa M và D; O và B nằm về hai phía so với cát tuyến MCD).
a) Chứng minh: tứ giác MAOB nội tiếp. b) Chứng minh: 2
MB  MC.MD
c) Gọi H là giao điểm của AB và OM. Chứng minh: AB là phân giác của góc CHD. Vẽ hình đến câu a 0,25đ Câu 5 Ta có:     90O OAM OBM
(vì MA, MB là các tiếp tuyến của (O) ) 0,25đ (2,5 a)   điểm): (0,75đ)   180O OAM OBM 0,25đ
 tứ giác MAOB nội tiếp. 0,25đ
Xét MBC và MDB có: 0,125đ   BMD chung   0,125đ   1 
MBC  MDB ( sd BC) 0,125đ b)  2 (0,75đ)  MB  C  MD  B (g-g) 0,125đ MB MC   MD MB 0,125đ 2
 MB  MC.MD (1) 0,125đ  0 2
MOBcó B  90 ; BH  OM  MB  MH.MO (2) 0,125đ 0,125đ
(1) & (2)  MC.MD = MH.MO ét X MCH & MO  D có:  DMO chung  0,125đ  MC MH c)   ( ì v MC.MD = MH.MO)  MO MD (0,75đ) 0,125đ  
 MCH  MOD (c.g.c)  MHC  ODM (3)
tứ giác OHCD nội tiếp      
 OHD  OCD; mà OCD  ODM (OCD cân)  OHD  ODM (4) 0,125đ       0
(3) & (4)  MHC  OHD do MHC  CHB  OHD  DHB  90   0,125đ
 CHB  DHB  AB là phân giác của  CHD
Ghi chú: HS làm cách khác đúng vẫn cho điểm tối đa