SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT BÌNH PHƯỚC
NĂM HỌC 2018 – 2019
MÔN THI: TOÁN CHUYÊN ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề)
(Đề thi gồm có 01 trang) Ngày thi: 03/06/2018
Câu 1. (2,0 điểm).  a 1 ab  a   a 1 ab  a 
a) Rút gọn biểu thức T    1 :  1  ab 1 ab 1   ab 1 ab 1         
b) Cho x  3  2. Tính giá trị của biểu thức: H  x 5  x 4  x 3  x 2 3 3 6  2 x 0  2023 1 1
Câu 2. ( 1,0 điểm). Cho Parabol P
( ) : y  x2 và đường thẳng d
( ) : y  m  1x  m2  (m là tham số). 2 2
Với giá trị nào của m thì đường thẳng d ( ) cắt Parabol P
( ) tại hai điểm A x ( ;y ),B x
( ;y ) sao cho biểu thức 1 1 2 2
T  y  y  x x đạt giá trị nhỏ nhất. 1 2 1 2
Câu 3. (2,0 điểm).
a) Giải phương trình: x   x   x2 1 6 14  5  2  x    2 1 y   1  10
b) Giải hệ phương trình:    x  y  xy   1  3
Câu 4. (3,0 điểm). Cho đường tròn O;R có hai đường kính AB và CD vuông góc với nhau. Trên dây BC 1
lấy điểm M ( M khác B và C ). Trên dây BD lấy điểm N sao cho  
MAN  CAD ; AN cắt CD tại K . 2
Từ M kẻ MH  AB H AB .
a) Chứng minh tứ giác ACMH và tứ giác ACMK nội tiếp.
b) Tia AM cắt đường tròn O  tạiE (E khác A ). Tiếp tuyến tại E và B của đường tròn O  cắt nhau tạiF .
Chứng minh rằng AF đi qua trung điểm của HM .
c) Chứng minh MN luôn tiếp xúc với một đường tròn cố định khi M di chuyển trên dây BC M khác B và C .
Câu 5. (1,0 điểm).
a) Tìm tất cả các số nguyên tố p sao cho 16p 1 là lập phương của số nguyên dương.
b) Tìm tất cả các bộ số nguyên a,b thỏa mãn  2 2
3 a b   7a b  4 
Câu 6. ( 1,0 điểm). x2 y2
a) Cho x,y là hai số dương. Chứng minh rằng: 
 x  y y x
b) Xét các số thực a,b,c với b  a  c sao cho phương trình bậc hai ax2  bx  c  0 có hai nghiệm thực
m,n thỏa mãn 0  m,n  1. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức a (  b)( a 2  c) M  a a (  b  c) HẾT
Lưu ý: Thí sinh không được sử dụng tài liệu, giám thị coi thi không giải thích gì thêm.
Họ và tên thí sinh:.....................................................Số báo danh:...................................................
Chữ ký của giám thị 1:..............................................Chữ ký của giám thị 2:.................................... Page 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM KÌ THI TUYỂN SINH BÌNH PHƯỚC
LỚP 10 THPT NĂM HỌC 2018-2019
Hướng dẫn chấm gồm 07 trang
MÔN THI: TOÁN CHUYÊN
Lưu ý: Điểm toàn bài lấy điểm lẻ đến 0,125; thí sinh làm cách khác đúng vẫn cho điểm tối đa. Điểm Câu Nội dung  a 1 ab  a   a 1 ab  a 
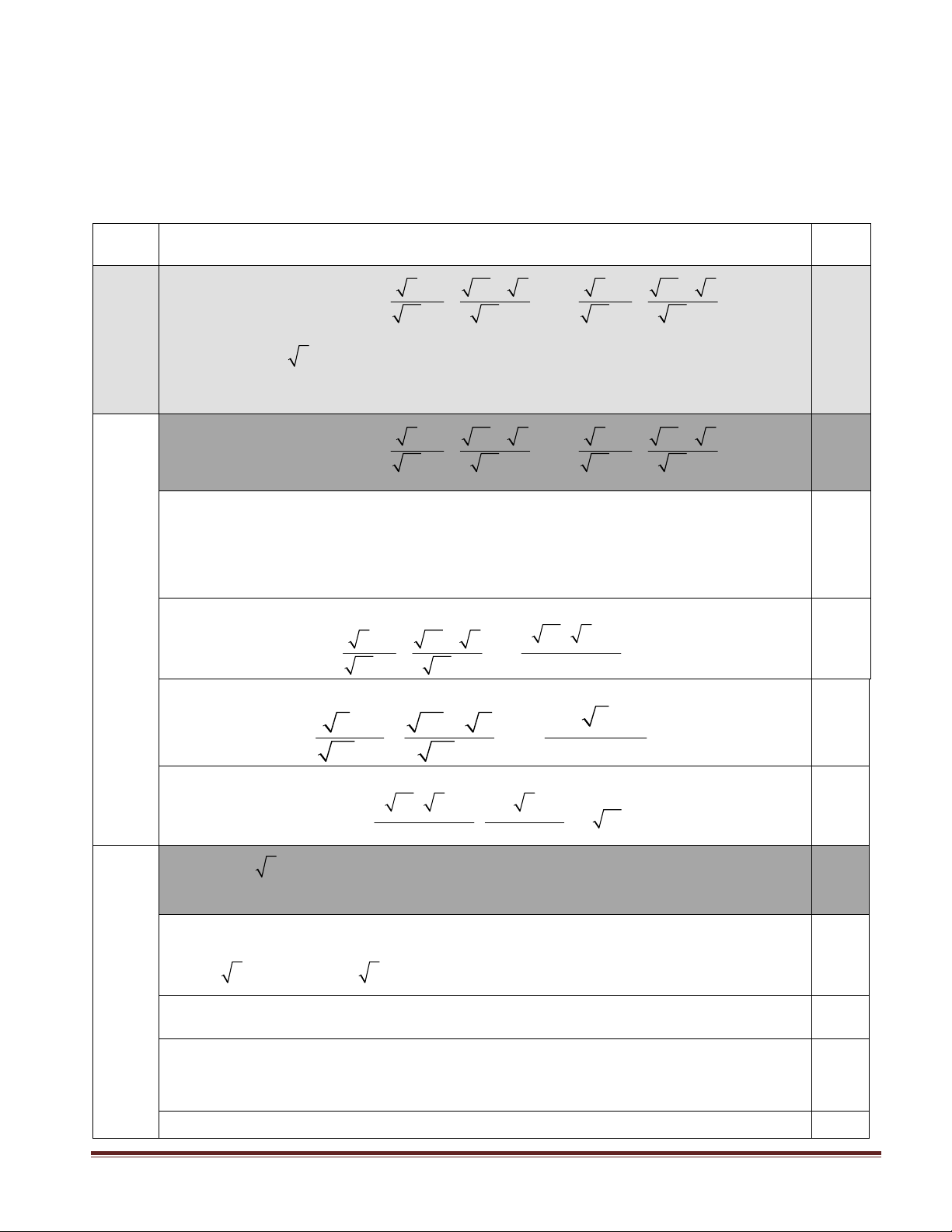
a) Rút gọn biểu thức T    1 :  1  . ab 1 ab 1   ab 1 ab 1          2,0 1
b) Cho x  3  2. Tính giá trị của biểu thức:
H  x 5  x 4  x 3  x2 3 3 6  2 x 0  2023.  a 1 ab  a   a 1 ab  a 
a) Rút gọn biểu thức T    1 :  1  . 1,0 ab 1 ab 1   ab 1 ab 1          a   0  0,25 Điều kiện: b   0 ab  1  Ta có: 2 ab  a 0,25 a ab a    1 1  1  . ab 1 ab 1 ab 1 Và 2 0,25 a  ab  a  a 1 1    1  . ab  1 ab  1 ab  1 Nên
2 ab  a   1 2   a   1 0,25 T  :   ab. ab 1 ab 1
b) Cho x  3  2. Tính giá trị của biểu thức: 1,0
H  x 5  x 4  x 3  x2 3 3 6  2 x 0  2023. Ta có : 0,25 2 x     x 
   x     x  x2   x2 3 2 2 3 2 3 4 4 3  x 4  1  0.
H  x5  x4  x3   x4  x3  x2   x2 4 4 5  x 4  1  2018. 0,25 Suy ra:
H  x 3 x2  x    x2 x2  x    x2 4 1 4 1 5  x 4  1  2018. 0,25 Do x2  x
4  1  0 nên H  2018. 0,25 Page 2 1 1 Cho Parabol P
( ) : y  x2 và đường thẳng d
( ) : y  m  1x  m2  (m là tham số). 2 2 1,0
Với giá trị nào của m thì đường thẳng d ( ) cắt Parabol P ( ) tại hai điểm A x ( ;y ),B x
( ;y ) sao cho biểu thức T  y  y  x x đạt giá trị nhỏ nhất. 1 1 2 2 1 2 1 2
Phương trình hoành độ giao điểm: 1 1 0,125
x 2  m 1x m2   x2  2m 1x  m2 2 1  0 ( ) 1 2 2 Để d ( ) cắt P
( ) tại hai điểm A x ( ;y ),B x
( ;y ) thì phương trình (1) có hai nghiệm. 1 1 2 2
D'   m  2  m2   m  m2 0 1 2 1 2
 0  0  m  2. 0,25
Vậy với 0  m  2 thì đường thẳng d ( )cắt Parabol P
( ) tại hai điểm A x ( ;y ),B x ( ;y ) . 1 1 2 2
Khi đó theo định lý Viet thì x   x   2 1 1 2 m   2  x  x  m2 2   1 1 2 Ta có 0,125 1 y  m (  1 x )  m2  1 1 2 1 y  m (  1 x )  m2  1 2 2 Do đó
T  y y x x  m   1 x x  2
 2m 1x x 1 2 1 2 1 2 1 2 0,125  2m  2 1  4m  2  2
 m  4m  2  2m  2 2 2 1 , m  0,  2 .
Đặt t  m 1. Do m   t   2 0, 2 1,1  t 0,  1 . 0,25
Nên T   m  2 2 2 2 1  2  2t  0.
Vậy giá trị nhỏ nhất của T bằng 0 đạt được khi t   m  2 2 1
1  1  m  0;m  2. 0,125
a) Giải phương trình: x   x   x2 1 6 14  5 3  2 x   2 1 y   1  10 2,0
b) Giải hệ phương trình: 
x yxy   1  3
a) Giải phương trình: x   x   x2 1 6 14  5. 1,0 7
Điều kiện: x  . 3 0,125
Nhận xét: với điều kiện trên thì vế phải của phương trình luôn dương. Ta có: 0,25 2 2
x 1  6x 14  x  5  x 1  2  6x 14  2  x  9. x  3 6x  3  
 x 3x  3  0. 0,25 x 1  2 6x 14  2     x   1 6 3    x 3  0.  0,125  x 1  2 6x 14  2  Page 3 x   3  0 x   3  0,125 1 6        x   1 6 3  0  
 x  3 *.  x 1  2 6x 14  2  x 1  2 6x 14  2 VT   7 *   2  7  Ta có :  x    PT     * VN. 0,125 VP    16  3 *    3
Vậy phương trình có nghiệm duy nhất x  3.  2  x    2 1 y   1  10
b) Giải hệ phương trình:  . 1,0   x  y  xy   1  3  2  x    2 2 2 2 2 1 (y 1)  10 x
 y x y 110 
 x y2 xy  2 1  10      I   0,125  x  y  xy  1  3   x  y  xy   1  3   x y  xy  1  3 x   y  u Đặt  . xy  1  v Khi đó, ta có: 0,125 2 2 2 2             I  u v 10 u v 2uv 10 u v 16       uv   3 uv   3 uv   3  u   1 v   3 u  v 4     u   3    uv   3  v  1     0,125 u  v  4  u   1        uv 3 v   3   u   3  v   1  u  1 x  y 1 - Với    HPTVN  v 0,125   3 xy   4  x  1  u   3 x  y  3 y   2 - Với      0,125 v   1 xy   2 x   2  y   1  x   1  u   1  x  y  1  y   2  0,125 - Với     v   3  xy   2   x   2    y   1  x   0  u   3  x  y  3  y   3  - Với      0,125 v   1  xy   0 x   3   y    0 Page 4
Vậy hệ phương trình có các nghiệm là:
1;2,2; 1,1;2,2; 1,0;3,3;0 0,125
Cho đường tròn O;R có hai đường kính AB và CD vuông góc với nhau. Trên dây BC 1
lấy điểm M ( M khác B và C ). Trên dây BD lấy điểm N sao cho   MAN  CAD ; 2
AN cắt CD tại K .Từ M kẻ MH  AB H AB . 4
a) Chứng minh tứ giác ACMH và tứ giác ACMK nội tiếp. 3,0
b) Tia AM cắt đường tròn O  tạiE (E khác A ). Tiếp tuyến tại E và B của đường
tròn O  cắt nhau tạiF . Chứng minh rằngAF đi qua trung điểm của HM .
c) Chứng minh MN luôn tiếp xúc với một đường tròn cố định khi M di chuyển trên
dây BC M khác B và C .
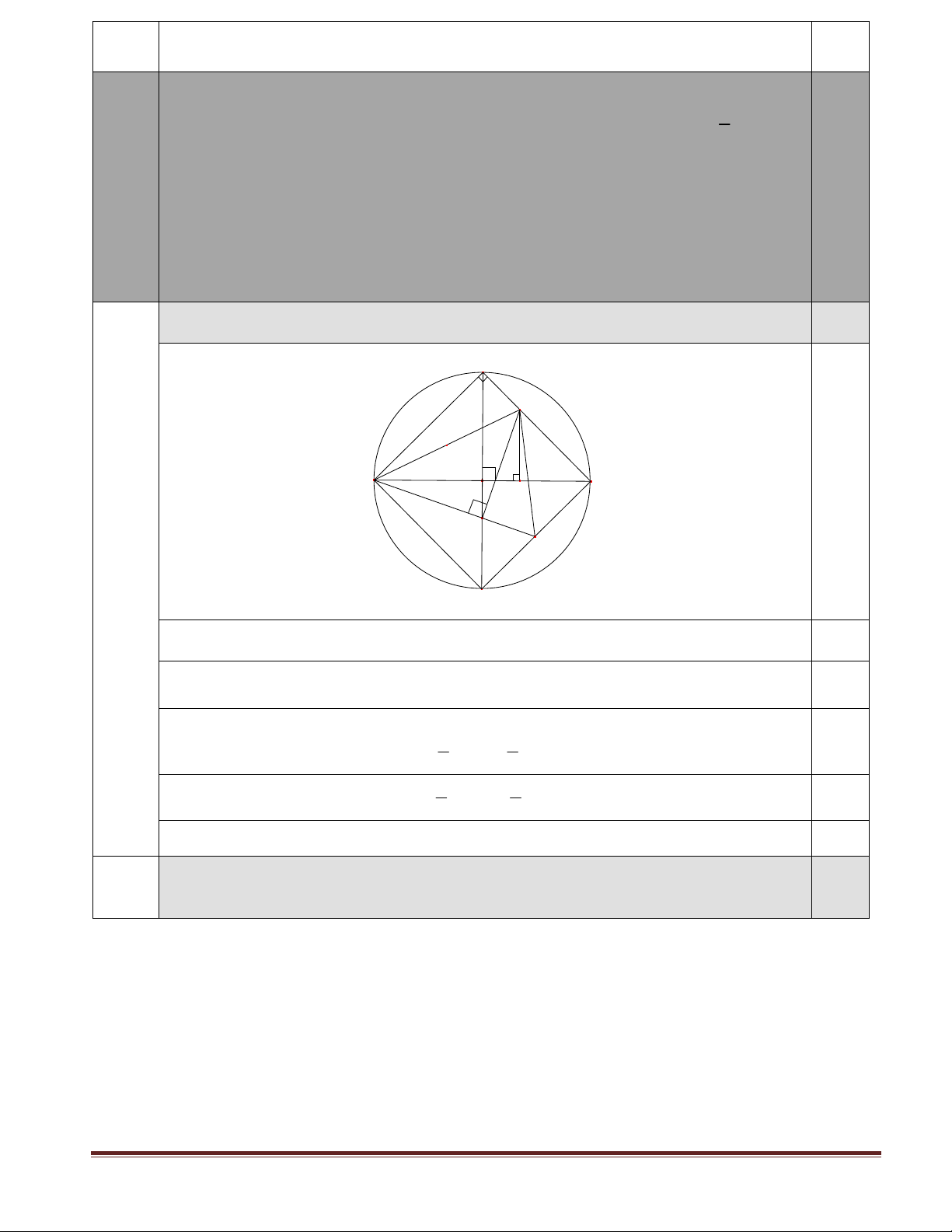
a) Chứng minh tứ giác ACMH và tứ giác ACMK nội tiếp. 1,25 C M A O B H K N D Ta có:  0
ACB  90 ( góc nội tiếp chắn nửa đường tròn) hay  0 ACM  90 . 0,25   0   0
ACM  AHM  90  ACM  AHM  180  tứ giác ACMH nội tiếp. 0,25 Ta lại có: 0,25  1  1 0 0
MAK  CAD  .90  45 . 2 2  1  1 0 0
MCK  sđ DB  .90  45 0,25 2 2  
 MAK  MCK  tứ giácACMK nội tiếp. 0,25
b) Tia AM cắt đường tròn O  tại E (E khác A ). Tiếp tuyến tại E và B của đường
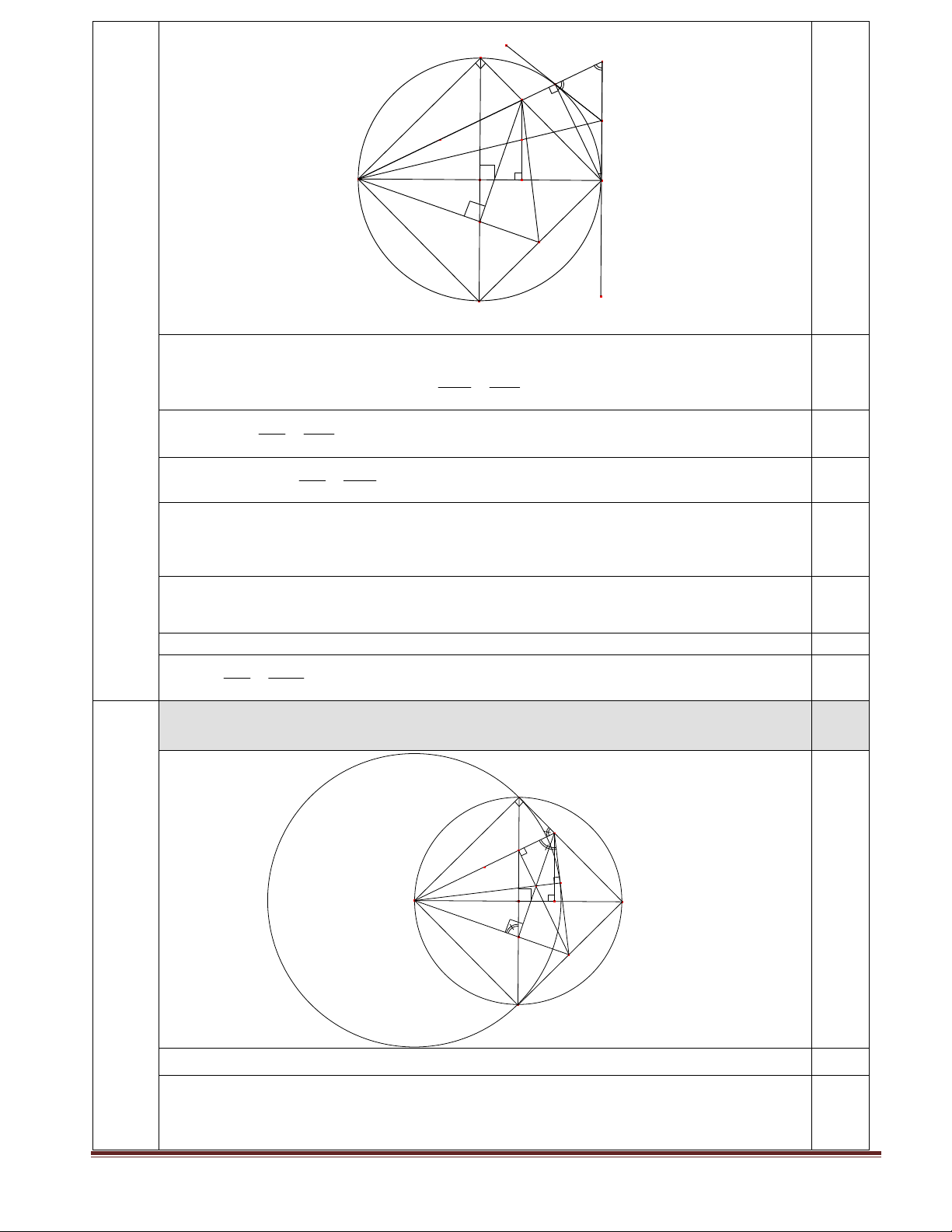
tròn O  cắt nhau tại F . Chứng minh rằngAF đi qua trung điểm của HM . 1,0 Page 5 C E P M F I A O B H K N D
Gọi AF MH  I;AM BF  P. MH AH 0,125
MH / /PB vì cùng vuông góc AB     1 PB AB IH AH IH / /FB   2 FB AB 0,125 IH MH Từ   1 ,2 suy ra  . 0,125 FB PB Ta có:  0  0
AEB  90  BEP  90 . 0,125
Theo tính chất hai tiếp tuyến cắt nhau thì  
 FE  FB  FEB  FBE.  0   0 
FEP  90  FEB;FPE  90  FBE. ;  
 FEP  FPE  FE  FP. 0,125
Vì FE  FP và FE  FB do đó FB  FP mà F BP  BP  2FB. 0,125 IH MH Suy ra: 
 MH  2IH  AF đi qua trung điểm I của MH . 0,25 FB 2FB
c) Chứng minh rằng: MN luôn tiếp xúc với một đường tròn cố định khi M di chuyển
trên dây BC M khác B và C . 0,75 C M G Q A O B H K N D
Vì tứ giác ACMK nội tiếp   0
 ACM  MKN  90 . 0,125
Gọi giao điểm của AM và dây DC là G.
Tứ giác ADNG có   0
NAG  NDG  45  tứ giác ADNG nội tiếp. 0,125   0
 ADN  MGN  90 . Page 6 Vì   0
MKN  MGN  90  tứ giác MGKN nội tiếp  
 AMN  AKC. 0,125 Mà  
AMC  AKC vì cùng chắn  AC nên   AMC  AMN . 0,125
Kẻ AQ vuông góc với MN tại Q . Khi đó A  MC  A
 MQ ch gn  AQ  AC. 0,125 Trong đó: 2 2
AC  R  R  R 2 không đổi và A là một điểm cố định nên khi M di
chuyển trên dây BC thì MN luôn tiếp xúc với đường tròn  ;
A R 2  là một đường tròn 0,125 cố định.
a) Tìm tất cả các số nguyên tố p sao cho 16p 1 là lập phương của số nguyên dương. 1,0 5
b) Tìm tất cả các bộ số nguyên a,b thỏa mãn  2 2
3 a b   7a b  4  .
a) Tìm tất cả các số nguyên tố p sao cho 16p 1 là lập phương của số nguyên dương. 0,5 0,125
Vì 16p 1 là lẻ và lớn hơn 1 nên có thể đặt p    n  3 * 16 1 2 1 , n    . Ta có:
p    n  3  p  n  2 16 1 2 1 8
4n  6n  3 0,125 Vì 2
4n  6n  3 là số lẻ lớn hơn 1 và không phân tích được thành tích của hai số nguyên n   8 0,125 nên từ trên suy ra  2
4n  6n  3  p
Từ đó, ta có p  307. Thử lại ta thấy thỏa mãn. Vậy p  307 là số nguyên tố duy nhất 0,125 thỏa mãn yêu cầu.
b) Tìm tất cả các bộ số nguyên a,b thỏa mãn  2 2
3 a b   7a b  4  . 0,5
Nhân cả hai vế 12 , ta được:
a b  a b     a  2  b  2 2 2 36 84 48 6 7 6 7  50 0,125
Số 50 có thể phân tích thành tổng của hai số chính phương là 50  25  25  1 49 0,125 Page 7
Nhận xét: Do vai trò của a,b như nhau nên nếu a,b thỏa mãn thì b,a  cũng thỏa mãn.
Nên chỉ cần xét các trường hợp sau: TH1: a  2  b  2 6a  7  5   a  2 6a  7  5   1 6a 7 5 b       3    6a  72  25 6a  7  5       1 a      6b  72  25 6a  7  5     3    6a  7  5  b  2  0,125 6a 7 5      1  a  6  a  7  5    3   1   b   3 TH2:  4 a   3 6a 7 1      7  b  6b  7  7  3  6a 7 1  4  a     6a  72 1 6b  7  7    3      b  b    a      6 72 0 49 6 7 1    b   a  1 6 7 7    7 6a  7  1  b     3 6  b  7  7   a  1  b  0
Kết hợp với giả thiết và nhận xét ở trên, ta có các bộ số a,b thỏa mãn là:  0,125 0,  1 ;1,0,2, 2 x 2 y2
a) Cho x,y là hai số dương. Chứng minh rằng: 
 x  y. y x
b) Xét các số thực a,b,c với b  a  c sao cho phương trình bậc hai 1,0 6
ax 2  bx  c  0 có hai nghiệm thực m,n thỏa mãn 0  m,n  1. Tìm giá trị lớn
nhất và giá trị nhỏ nhất của biểu thức a (  b)( a 2  c) M  a a (  b  c) x 2 y2 0,5
a) Cho x,y là hai số dương. Chứng minh rằng: 
 x  y. y x 2 2 x y
Với x,y là hai số dương 3 3 
 x y  x y  xy x y. 0,125 y x Page 8
 x y 2 2
x xy y   xy x y. 0,125
x  xy  y  xy  x  xy  y   x y 2 2 2 2 2 2 0  0 (hiển nhiên). 0,125
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi x  y  0. 0,125
b) Xét các số thực a,b,c với b  a  c sao cho phương trình bậc hai ax2  bx  c  0 có 0,5
hai nghiệm thực m,n thỏa mãn 0  m,n  1. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức a (  b)( a 2  c) M  a a (  b  c)
Giả thiết phương trình ax2  bx  c  0 có hai nghiệm ,
m n 0  m  1,0  n  1 nên b c 0,125
a  0. Theo định lí Viete, ta có: m  n   và m n .  a a  b   c  1   2   a (  b)( a 2  c) a a    
1  m  n2 mn Từ đó suy ra: M    . a a (  b  c) b c
1  m  n  mn 1   0,125 a a
Vì 2  mn  2 và mn  0 nên
1m n.2 M   2. 1  m  n 0,125
Vậy giá trị lớn nhất của M là 2 đạt được khi mn  0 hay c  0.
Do 0  m  1, 0  n  1 nên mn  1, suy ra: 1
m n  1  n m  1  mn  1  0  mn  1  m  n. 3 Do đó: 0,125 1  m  n 3 M   .  1 4
1 m  n  1  m  n 3 3
Vậy giá trị nhỏ nhất của M là đạt được khi m  n  1 hay a  b  c  0 và a  c. 4 Page 9