

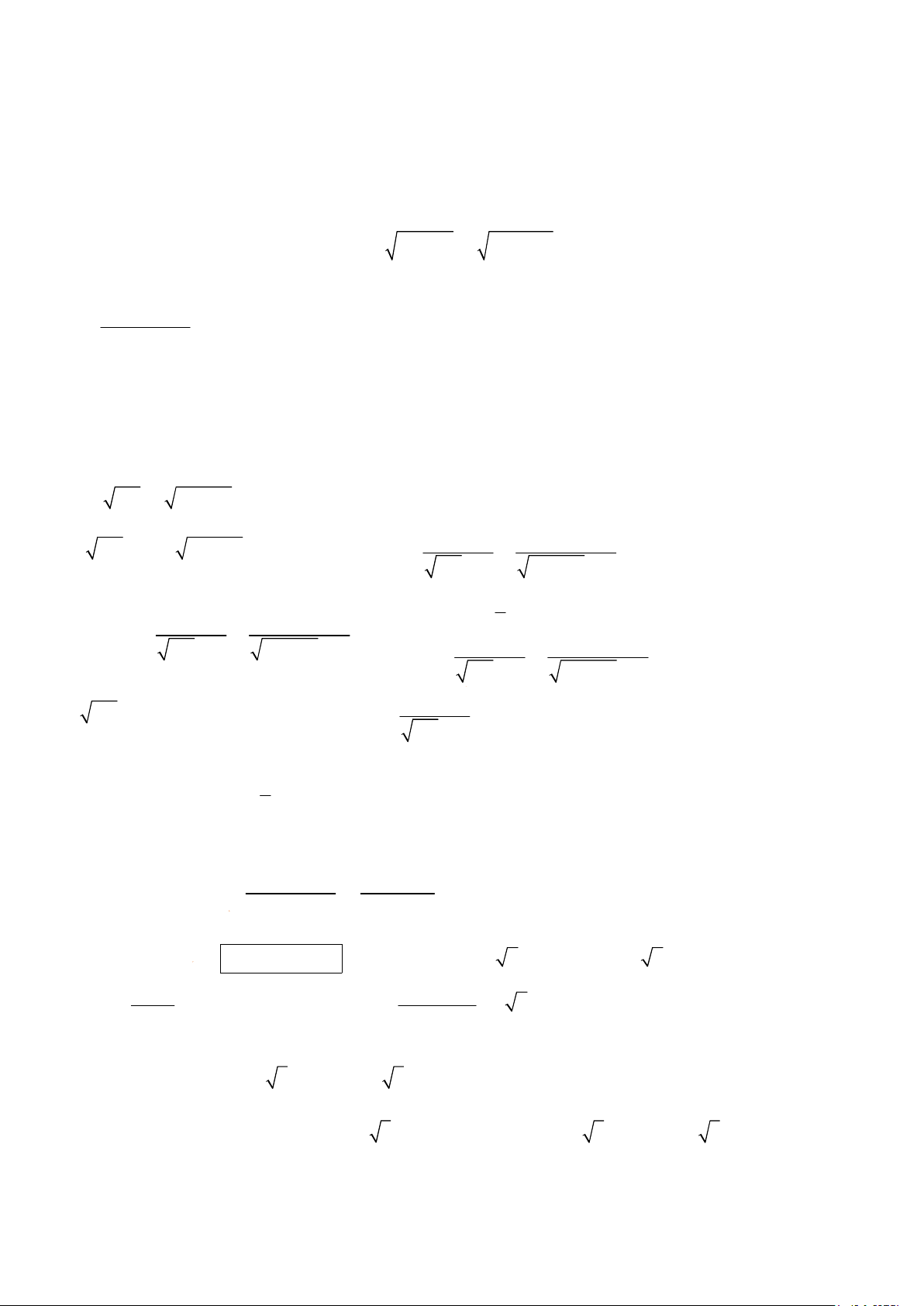
Preview text:
UBND TỈNH BẮC NINH
ĐỀ TUYỂN SINH VÀO LỚP 10 THPT
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2019 - 2020 MÔN THI: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút (không kể thời gian giao đề) -----------------------
I. TRẮC NGHIỆM (3,0 ñiểm) Chọn phương án trả lời ñúng trong các câu sau: 4 Câu 1:
Khi x = 7 biểu thức có giá trị là x + 2 − 1 1 4 4 A. . B. . C. . D. 2 . 2 8 3 Câu 2:
Trong các hàm số sau, hàm số nào ñồng biến trên ℝ ?
A.y = 1 − x .
B. y = 2x − 3 .
C. y = (1− 2)x . D.y = −2x + 6. Câu 3:
Số nghiệm của phương trình 4 2
x − 3x + 2 = 0 là A.1 . B. 2 . C. 3 . D. 4 . Câu 4: Cho hàm số 2
y = ax (a ≠ 0). ðiểm M (1;2) thuộc ñồ thị hàm số khi 1 1 A.a = 2 . B.a = . C.a = 2 − . D.a = . 2 4 Câu 5:
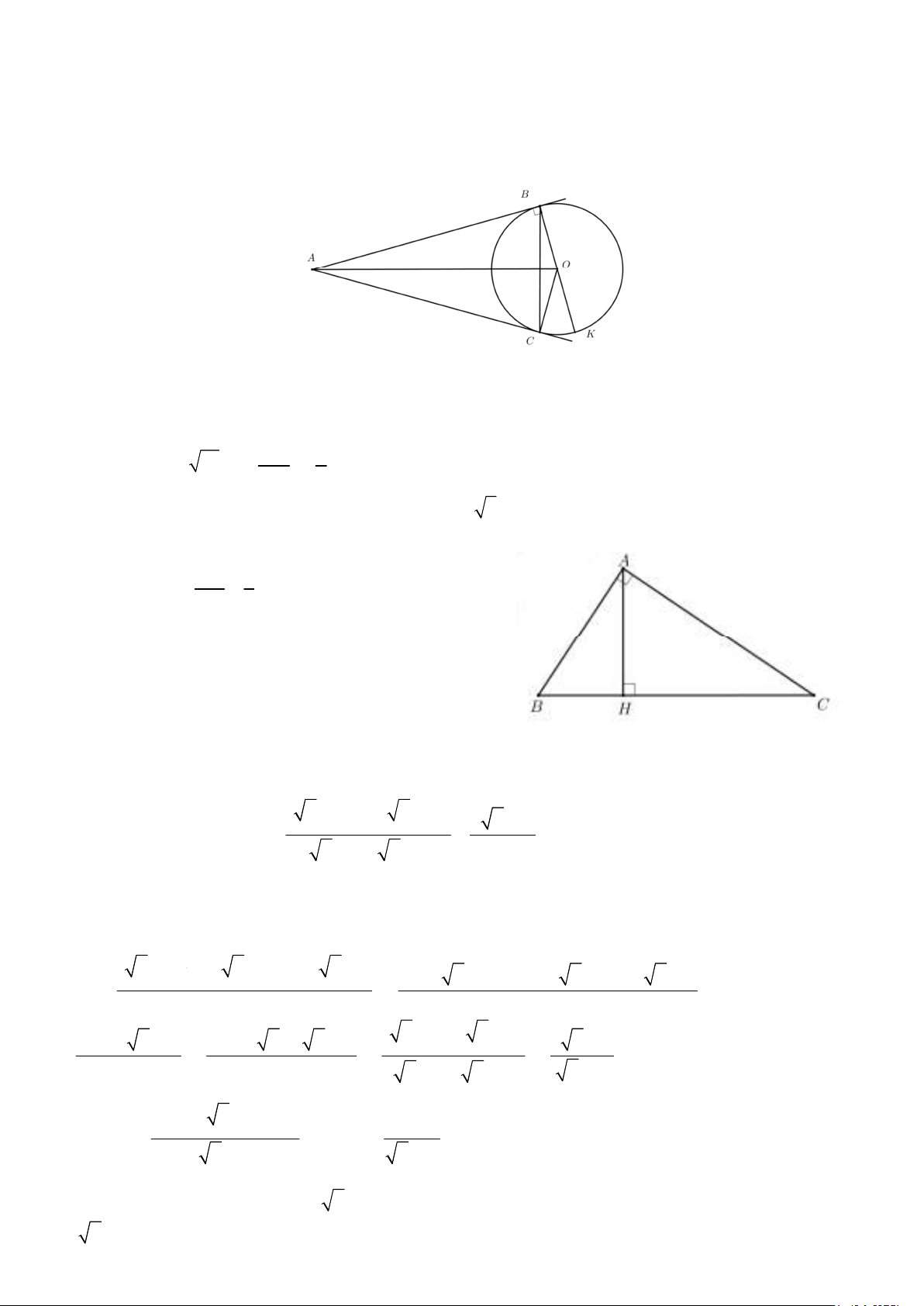
Từ ñiểm A nằm bên ngoài ñường tròn (O) kẻ hai tiếp tuyến AB,AC tới ñường tròn (B,C là các
tiếp ñiểm). Kẻ ñường kính BK . Biết BAC = 30 ,số ñocủa cung nhỏ CK là A. 30° . B. 60° . C.120° . D.150° . Câu 6:
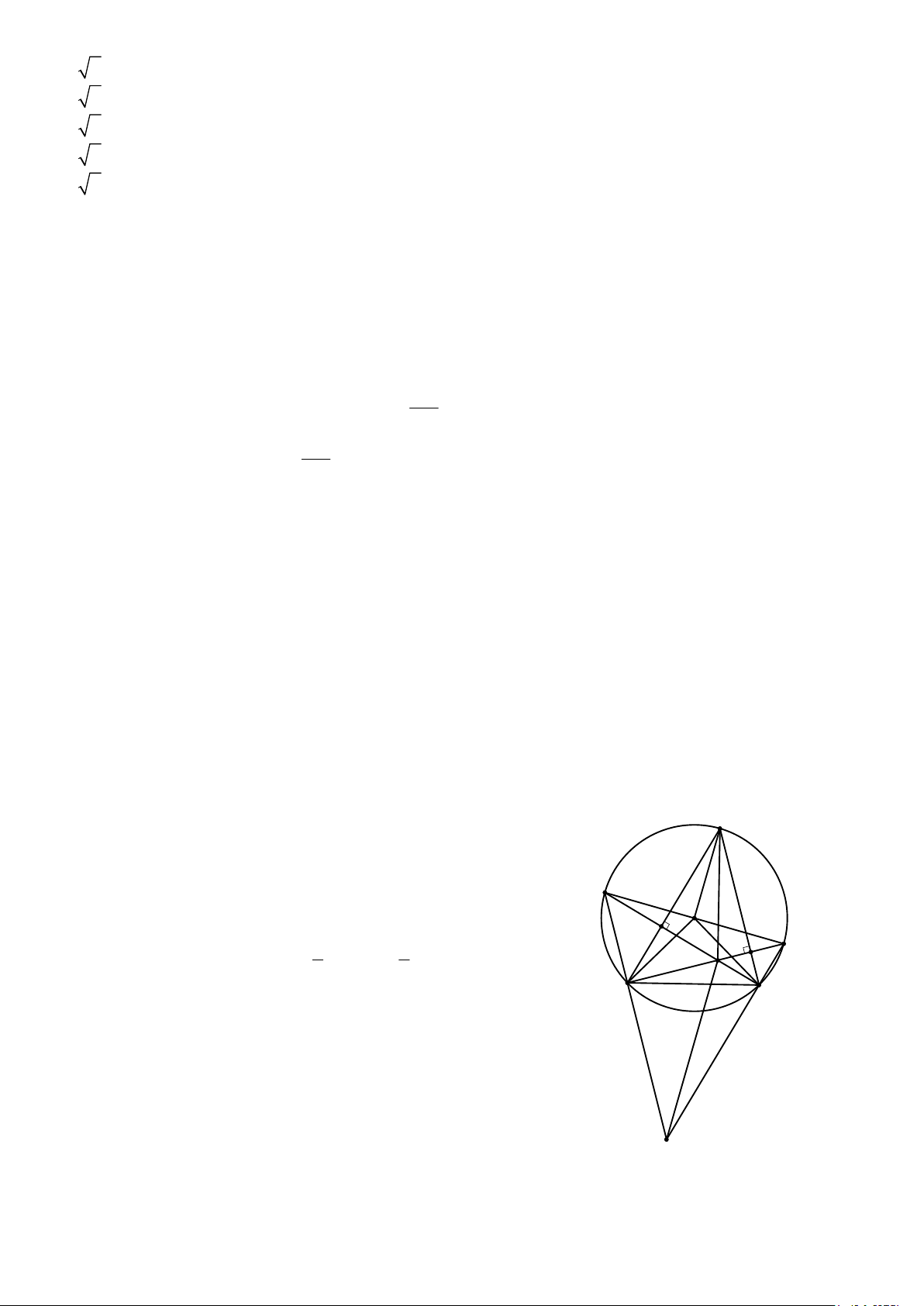
Cho tam giác ABC vuông tại A . Gọi H là chân ñường cao hạ từ ñỉnh A xuống cạnh BC . Biết HB 1 AH = 12cm , =
. ðộ dài ñoạn BC là HC 3 A. 6cm . B. 8cm .
C. 4 3cm . D.12cm .
II. TỰ LUẬN (7,0 ñiểm)
( x + )2 +( x − )2 1 1 3 x + 1
Câu 7: Cho biểu thức A = −
với x ≥ 0 , x ≠ 1 . ( x − )( x + ) x − 1 1 1
a) Rút gọn biểu thức A .
b) Tìm x là số chính phương ñể 2019A là số nguyên.
Câu 8: An ñếm số bài kiểm tra một tiết ñạt ñiểm 9 và ñiểm 10 của mình thấynhiều hơn16 bài. Tổng số
ñiểm của tất cả các bài kiểm tra ñạt ñiểm 9 và ñiểm 10 ñó là 160 . Hỏi An ñược bao nhiêu bài
ñiểm 9 và bao nhiêu bài ñiểm 10 ?
Câu 9: Cho ñường tròn (O), hai ñiểm ,
A B nằm trên (O) sao cho AOB = 90º . ðiểm C nằm trên cung
lớn AB sao cho AC > BC và tam giác ABC có ba góc ñều nhọn. Các ñường cao AI, BK của
tam giác ABC cắt nhau tại ñiểm H . BK cắt (O) tại ñiểmN (khác ñiểmB ); AI cắt (O) tại
ñiểm M (khác ñiểm A ); NA cắt MB tại ñiểm D . Chứng minh rằng:
a) Tứ giác CIHK nội tiếp một ñường tròn.
b) MN là ñường kính của ñường tròn (O).
c) OC song song với DH .
Câu 10: a) Cho phương trình 2
x − 2mx − 2m − 1 = 0 ( )
1 với m là tham số. Tìm m ñể phương trình ( ) 1 có
hai nghiệm phân biệt x , x sao cho x + x + 3 + x x = 2m + 1. 1 2 1 2 1 2
b) Cho hai số thực không âm , a b thỏa mãn 2 2
a + b = 2 . Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 3 3 a + b + 4 M = . ab + 1 ----------Hết--------- BẢNG ðÁP ÁN 1 2 3 4 5 6 D B D A A B
I. TRẮC NGHIỆM (3,0 ñiểm) Chọn phương án trả lời ñúng trong các câu sau: 4
Câu 1: Khi x = 7 biểu thức có giá trị là x + 2 − 1 1 4 4 A. . B. . C. . D. 2 . 2 8 3 Lời giải Chọn: D 4
Thay x = 7 (thỏa mãn) vào biểu thức
ta tính ñược biểu thức có giá trị bằng x + 2 −1 4 4 = = 2 . 7 + 2 −1 3 −1
Câu 2: Trong các hàm số sau, hàm số nào ñồng biến trên ℝ ? A.y = 1 − x .
B. y = 2x − 3 .
C.y = (1− 2)x . D.y = −2x + 6. Lời giải Chọn: B
Hàm số y = 2x − 3 ñồng biến trên ℝ .
Câu 3: Số nghiệm của phương trình 4 2
x − 3x + 2 = 0 là A.1 . B. 2 . C. 3 . D. 4 . Lời giải Chọn: D ðặt 2
t = x (t ≥ 0) . Khi ñó phương trình tương ñương 2
t − 3t + 2 = 0 .
Ta thấy 1- 3 + 2 = 0 . Nên phương trình có hai nghiệm t = 1 (thỏa mãn); t = 2 (thỏa mãn). 2 x =1 x = ±1 Khi ñó ⇒ ⇔ 2 x = 2 x = ± 2 Câu 4: Cho hàm số 2
y = ax (a ≠ 0). ðiểm M (1; )
2 thuộc ñồ thị hàm số khi 1 1 A.a = 2 . B.a = . C.a = −2 . D.a = . 2 4 Lời giải
Chọn A .
Vì M (1;2) thuộc ñồ thị hàm số 2
y = ax (a ≠ 0) nên ta có 2 2 = .
a 1 ⇔ a = 2 (thỏa mãn).
Câu 5: Từ ñiểm A nằm bên ngoài ñường tròn (O) kẻ hai tiếp tuyến AB,AC tới ñường tròn (B,C là các
tiếp ñiểm). Kẻ ñường kính BK . Biết BAC = 30 , số ño của cung nhỏ CK là A. 30° . B. 60° . C.120° . D.150° . Lời giải Chọn: A.
Từ giả thiết ta suy ra tứ giác ABOC nội tiếp nên = BAC COK = 30° , mà COK = sñ CK nên
Số ño cung nhỏ CK là 30° .
Câu 6: Cho tam giác ABC vuông tại A . Gọi H là chân ñường cao hạ từ ñỉnh A xuống cạnh BC . Biết HB 1 AH = 12cm , =
. ðộ dài ñoạn BC là HC 3 A. 6 cm . B. 8 cm . C. 4 3 cm . D.12 cm . Lời giải Chọn: B HB 1 Theo ñề bài ta có:
= ⇒ HC = 3HB . Áp dụng hệ HC 3
thức lượng trong tam giác ABC vuông tại A có ñường cao 2
AH = BH.HC ⇔ 12 = BH .3BH AH ta có 2
⇔ BH = 4 ⇔ BH = 2
⇒ HC = 3.HB = 3.2 = 6
⇒ BC = HB + HC = 2 + 6 = 8 (cm)
II. TỰ LUẬN (7,0 ñiểm)
( x + )2 +( x − )2 1 1 3 x + 1
Câu 7: Cho biểu thức A = −
với x ≥ 0 , x ≠ 1 . ( x − )( x + ) x − 1 1 1
a) Rút gọn biểu thức A .
b) Tìm x là số chính phương ñể 2019A là số nguyên. Lời giải
( x + )2 +( x − )2 1 1 − 3 x − 1
x + 2 x + 1 + x − 2 x + 1 − 3 x − 1 a) A = = x − 1 x − 1
2x − 2 x − x + 1 ( x − )1(2 x x x − − + )1 2 3 1 2 x − 1 = = = = . x − 1 x − 1
( x − )1( x + )1 x + 1 2019(2 x + 2 − 3) 6057 2019A = = 4038 − . x + 1 x + 1 b)
2019A là số nguyên khi và chỉ khi x + 1 là ước nguyên dương của 6057 gồm: 1; 3;9;673, 2019;6057 .
+) x + 1 = 1 ⇔ x = 0 , thỏa mãn.
+) x + 1 = 3 ⇔ x = 4 , thỏa mãn.
+) x + 1 = 9 ⇔ x = 64 , thỏa mãn.
+) x + 1 = 673 ⇔ x = 451584 , thỏa mãn.
+) x + 1 = 2019 ⇔ x = 4072324 , thỏa mãn.
+) x + 1 = 6057 ⇔ x = 36675136 , thỏa mãn. Câu 8:
An ñếm số bài kiểm tra một tiết ñạt ñiểm 9 và ñiểm 10 của mình thấynhiều hơn16 bài. Tổng số
ñiểm của tất cả các bài kiểm tra ñạt ñiểm 9 và ñiểm 10 ñó là 160 . Hỏi An ñược bao nhiêu bài
ñiểm 9 và bao nhiêu bài ñiểm 10 ? Lời giải
Gọi số bài ñiểm 9 và ñiểm 10 của An ñạt ñược lần lượt là x, y (bài)(x,y ∈ ℕ).
Theo giả thiết x + y > 16 .
Vì tổng số ñiểm của tất cả các bài kiểm tra ñó là 160 nên 9x + 10y = 160 . Ta có = x +
y ≥ (x + y) 160 160 9 10 9 ⇒ x + y ≤ . 9 160
Do x + y ∈ ℕ và 16 < x + y ≤
nên x + y = 17 . 9 x + y = 17 x = 17 −y x = 10 Ta có hệ ⇔ ⇔ (thỏa mãn). 9
x + 10y = 160 9
(17 − y) + 10y = 160 y = 7
Vậy An ñược 10 bài ñiểm 9 và 7 bài ñiểm 10 .
Câu 9: Cho ñường tròn (O), hai ñiểm ,
A B nằm trên (O) sao cho AOB = 90º . ðiểm C nằm trên cung
lớn AB sao cho AC > BC và tam giác ABC có ba góc ñều nhọn. Các ñường cao AI, BK của
tam giác ABC cắt nhau tại ñiểm H . BK cắt (O) tại ñiểmN (khác ñiểmB ); AI cắt (O) tại
ñiểm M (khác ñiểm A ); NA cắt MB tại ñiểm D . Chứng minh rằng:
a) Tứ giác CIHK nội tiếp một ñường tròn.
b) MN là ñường kính của ñường tròn (O).
c) OC song song với DH . Lời giải a)Ta có C H K ⊥ KC
⇒ HKC + HIC = 90º +90º = 180º . H I ⊥ IC N
Do ñó,CIHK là tứ giác nội tiếp. O
b) Do tứ giác CIHK nội tiếp nên K 1 1 M
45º = ICK = BHI = sñBM + sñAN . I 2 2 H A ⇒ B
sñBM + sñAN = 90° .
Suy ra, sñMN = sñAB + s
( ñBM + sñAN ) hay = 90° + 90° = 180º
MN là ñường kính của (O). D
c) Do MN là ñường kính của (O) nên MA ⊥ DN,NB ⊥ DM . Do ñó, H là trực tâm tam giác DMN hay DH ⊥ MN .
Do I , K cùng nhìn AB dưới góc 90º nên tứ giác ABIK nội tiếp.
Suy ra, CAI = CBK ⇒ sñCM = sñCN ⇒ C là ñiểm chính giữa của cung MN ⇒ CO ⊥ MN .
Vì AC > BC nên ∆ABC không cân tại C do ñó C,O, H không thẳng hàng. Từ ñó suy ra CO //DH .
Câu 10: a) Cho phương trình 2
x − 2mx − 2m − 1 = 0 ( )
1 với m là tham số. Tìm m ñể phương trình ( ) 1 có
hai nghiệm phân biệt x , x sao cho x + x + 3 + x x = 2m + 1. 1 2 1 2 1 2
b) Cho hai số thực không âm , a b thỏa mãn 2 2
a + b = 2 . Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 3 3 a + b + 4 M = . ab + 1 Lời giải
a) ∆′ = m + m + = (m + )2 2 2 1 1 . Phương trình ( )
1 có hai nghiệm phân biệt khi và chỉ khi ∆′ > 0 ⇔ m ≠ 1 − .
Áp dụng ðL Vi-ét ta có x + x = 2m;x .x = 2 − m − 1 . 1 2 1 2
Ta có 2m + 2 − 2m = 2m + 1 ( ðK 0 ≤ m ≤ 1 (*) ) 2m − 1 2m − 1
⇔ 2m − 1 + 2 − 2m − 1 − (2m − ) 1 = 0 ⇔ − − (2m − ) 1 = 0 2m + 1 2 − 2m + 1 1 m = (t / m( ) * ) ⇔ ( m − ) 1 1 2 2 1 − − 1 = 0 ⇔ + − + 1 1 2m 1 2 2m 1 − − 1 = 0 ( ) 2 2m + 1 2 − 2m + 1 1
Vì 2m + 1 ≥ 1, ∀m thỏa mãn 0 ≤ m ≤ 1 ⇒
≤ 1 . Do ñó, VT (2) < 0 =VP (2) hay (2)vô 2m + 1 nghiệm. 1
Vậy giá trị cần tìm là m = . 2 b) Ta có 3 3 a + b + = ( 3 3 4 a + b + )
1 + 3 ≥ 3ab + 3 . Dấu bằng xảy ra khi và chỉ khi a = b = 1. 3 3 3(ab a b + + + ) 1 4
Vì ab + 1 > 0 nên M = ≥ = 3 . ab + 1 ab + 1
Do ñó, giá trị nhỏ nhất của biểu thức M là 3 ñạt ñược khi a = b = 1.
This image cannot currently be display ed. +) Vì 2 2 a + b = 2 nên Suy ra 3 3 a + b + ≤ ( 2 2 4
2 a + b ) + 4 = 2 2 + 4 . 1 3 3 a + b + 4 Mặt khác
≤ 1 do ab +1 ≥ 1. Suy ra M = ≤ 2 2 + 4 . ab +1 ab +1
Dấu bằng xảy ra khi và chỉ khi 2 2 a + b = 2
⇔ (a;b) = (0; 2) ∨ (a;b) = ( 2;0). a b = 0
Giá trị lớn nhất của biểu thức M là 4 + 2 2 ñạt ñược khi (a;b) = (0; 2) ∨ (a;b) = ( 2;0)
--------------- HẾT ---------------




