Đề Toán tuyển sinh lớp 10 THPT chuyên 2018 – 2019 sở GD và ĐT Nam Định (đề chung)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 TRƯỜNG THPT CHUYÊN NAM ĐỊNH
Năm học: 2018 – 2019
Môn thi: Toán (chung) – Đề 1 ĐỀ CHÍ NH THỨC
Dành cho học sinh thi vào các lớp chuyên tự nhiên
Thời gian làm bài: 120 phút
(Đề thi gồm: 01 trang)
Câu 1 (2,0 điểm)
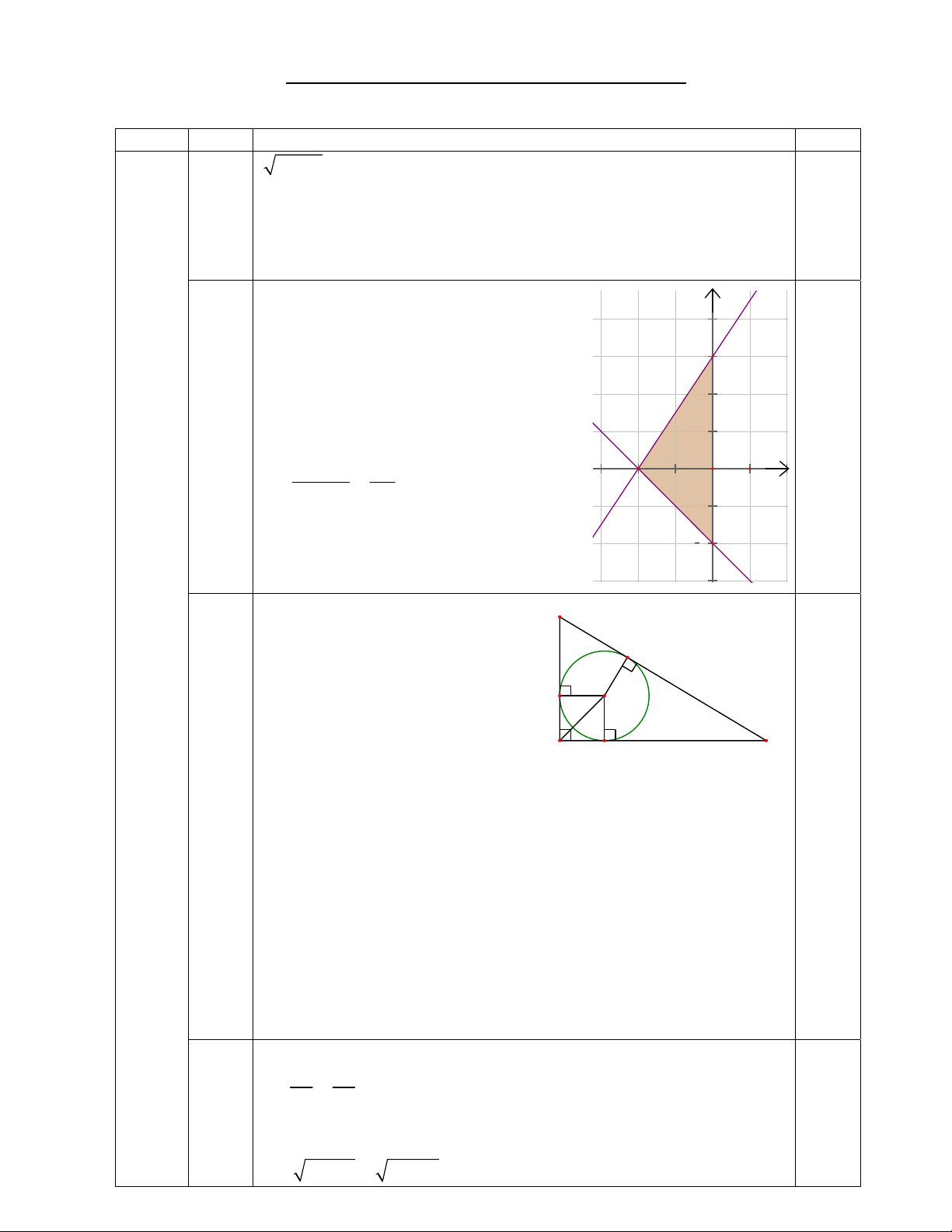
1) Giải phương trình 2x  3  x . 3
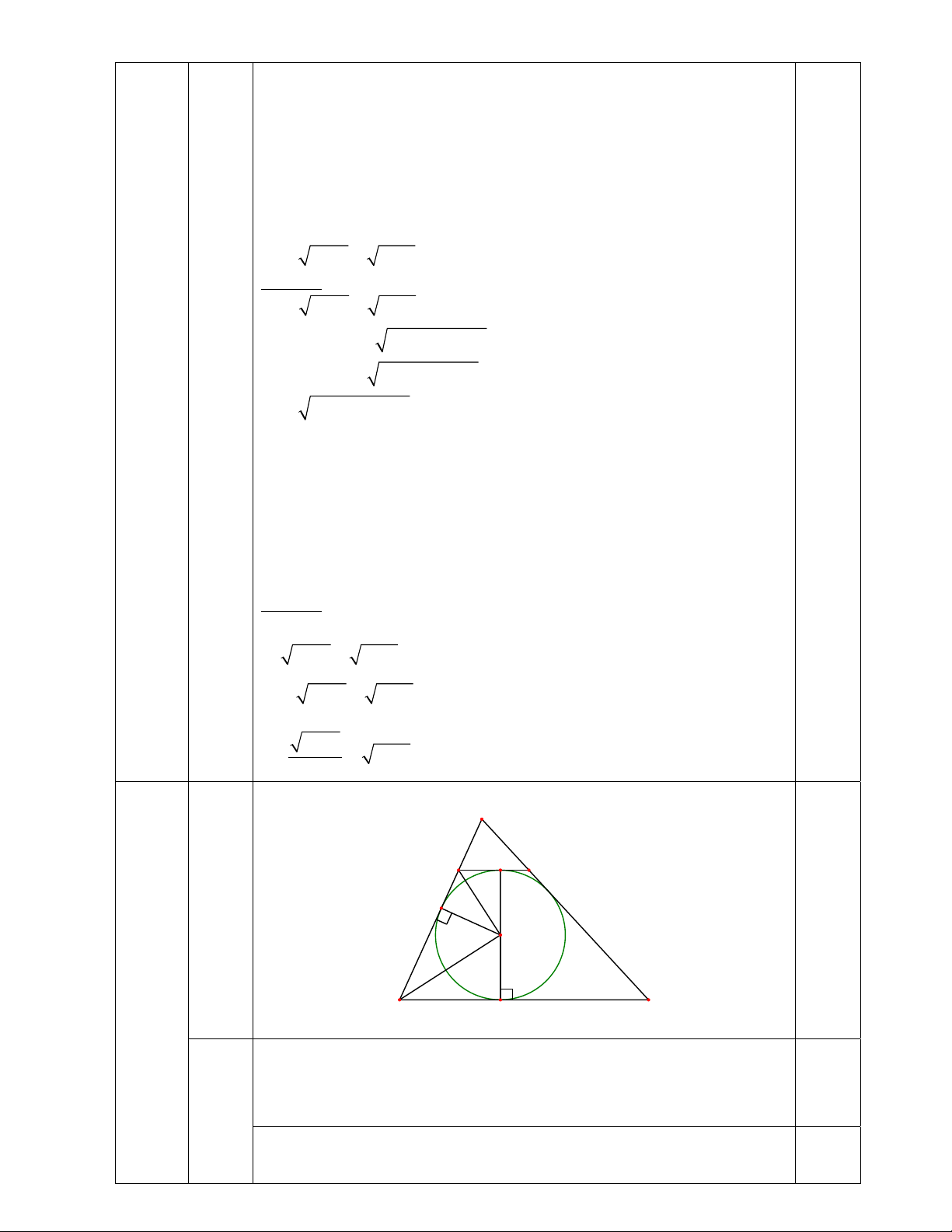
2) Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng y  x  2 (d ) và y  x  3 (d ) . Gọi A, 1 2 2
B lần lượt là giao điểm của (d1), (d2) với trục Oy và C là giao điểm của (d1) với (d2). Tính diện tích tam giác ABC.
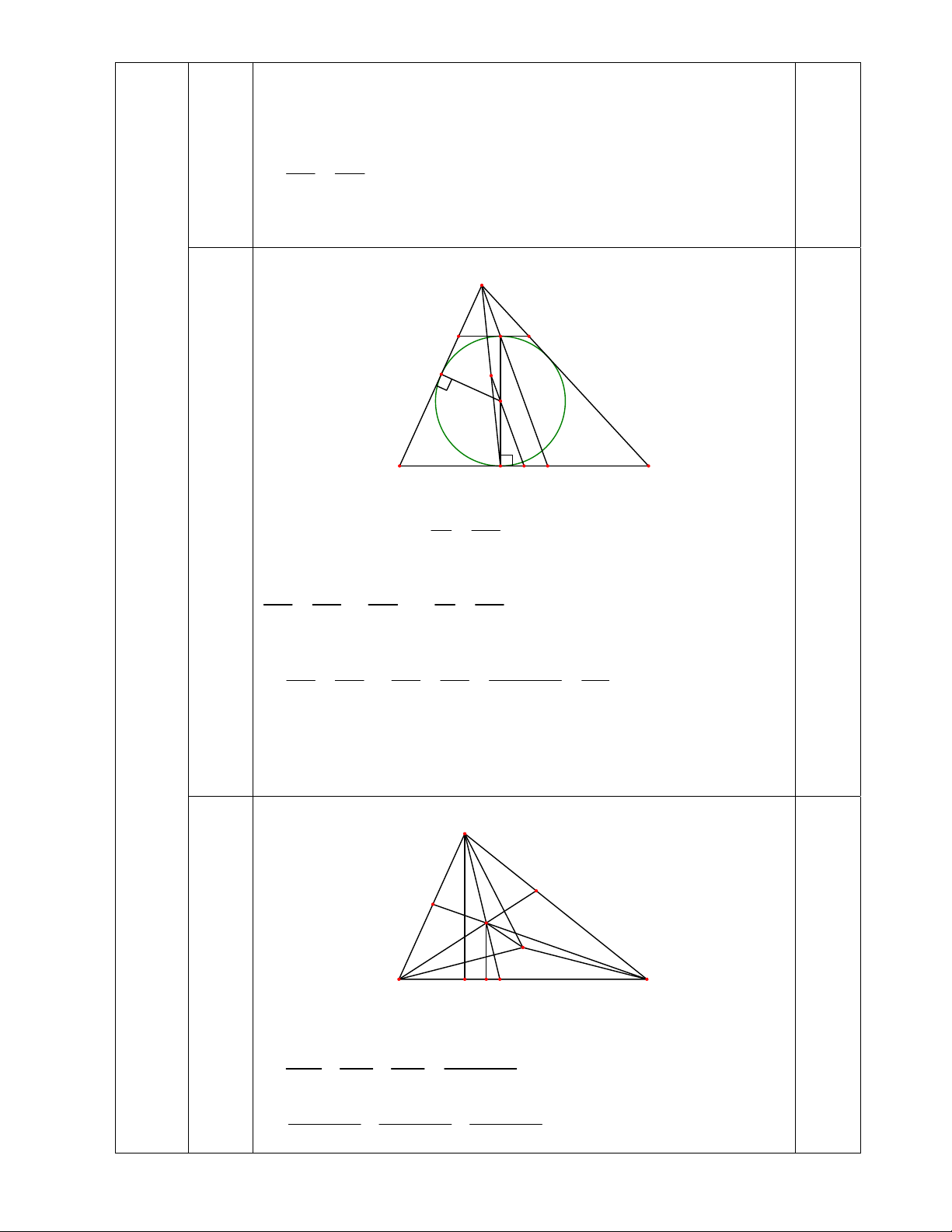
3) Cho tam giác ABC có AB  8(cm), BC  17(cm),CA  15(cm) . Tính chu vi đường tròn nội tiếp tam giác ABC.
4) Một hình nón có chu vi đường tròn đáy là 6 (cm) , độ dài đường sinh là 5(cm) . Tính thể tích hình nón đó. 
1   x 1 1 x 
Câu 2 (1,5 điểm) Cho biểu thức P  x  :    
 (với x  0 và x  1).  x   x x x    
1) Rút gọn biểu thức P.
2) Chứng minh rằng với mọi x  0 và x  1 thì P  4 .
Câu 3 (2,5 điểm) 1) Cho phương trình 2 2
x  mx  m  m  4  0 (với m là tham số).
a) Chứng minh với mọi giá trị của tham số m, phương trình đã cho luôn có hai nghiệm phân biệt.
b) Gọi x , x là hai nghiệm của phương trình đã cho (x  x ) . Tìm tất cả các giá trị của tham 1 2 1 2
số m để x  x  2 . 2 1 2) Giải phương trình 2
6 x  2  3 3  x  3x 1 4 x  x  6 .
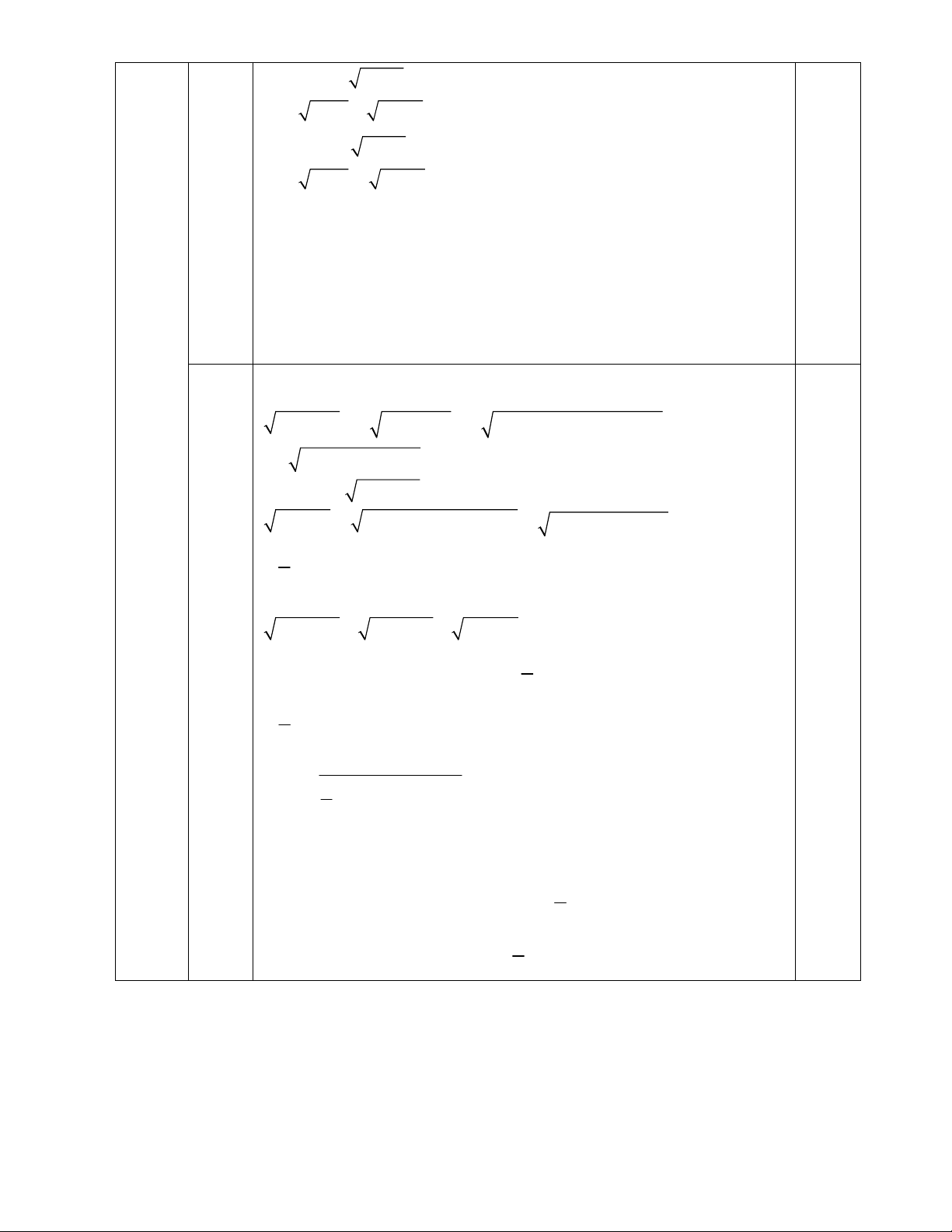
Câu 4 (3,0 điểm) Cho tam giác ABC (với AB < AC) ngoại tiếp đường tròn (O; R). Đường tròn (O; R)
tiếp xúc với các cạnh BC, AB lần lượt tại D, N. Kẻ đường kính DI của đường tròn (O; R). Tiếp tuyến
của đường tròn (O; R) tại I cắt các cạnh AB, AC lần lượt tại E, F.
1) Chứng minh tam giác BOE vuông và 2
EI.BD  FI.CD  R .
2) Gọi P, K lần lượt là trung điểm của các đoạn thẳng BC, AD; Q là giao điểm của BC và AI.
Chứng minh AQ  2KP .
3) Gọi A1 là giao điểm của AO với cạnh BC, B1 là giao điểm của BO với cạnh AC, C1 là giao điểm
của CO với cạnh AB và (O1; R1) là đường tròn ngoại tiếp tam giác ABC. 1 1 1 2 Chứng minh:    . AA BB CC R  OO 1 1 1 1 1
Câu 5 (1,0 điểm)
(2x  4y 1) 2x  y 1  (4x  2y  3) x  2y  (1)
1) Giải hệ phương trình  2 2
x  8x  5  2(3y  2) 4x  3y  2 2x  5x  2  (2)
2) Cho a, b, c là các số thực dương thỏa mãn ab  2bc  2ca  7 . Tìm giá trị nhỏ nhất của biểu
11a 11b 12c thức Q  . 2 2 2
8a  56  8b  56  4c  7
-------------------- HẾT --------------------
Họ và tên thí sinh: .............................................
Họ tên, chữ kí GT 1: ...........................
Số báo danh: ......................................................
Họ tên, chữ kí GT 2: ...........................
HƯỚNG DẪN GIẢI VÀ BIỂU ĐIỂM DỰ KIẾN: Câu Phần Nội dung Điểm
2x  3  x (1) (ĐK: x  0 ) x  1  2 2
 x  x   x  x    x  x    1) (1) 2 3 2 3 0 ( 1)( 3) 0  x  3 0.5
Kết hợp với điều kiện  x  3
Vậy nghiệm của phương trình là x = 3.
Đường thẳng (d1) đi qua các điểm y (0; – 2) và (– 2; 0) 4
Đường thẳng (d2) đi qua các điểm (0; 3) và (– 2; 0) B Theo đề bài, ta có:
A(0; – 2) , B(0; 3) , C(– 2; 0) 2  CO = 2; AB = 5 d 2) 1
Diện tích của  ABC là: 0.5 AB.OC 5.2 S  
 5 (đơn vị diện tích) O x C 2 2 d2 2 A Ta có: BC2 = 172 = 289 B Câu 1 AB2 + AC2 = 82 + 152 = 289 F (2,0đ)  BC2 = AB2 + AC2
  ABC vuông tại A (định lí D O Py-ta-go đảo)
Vẽ (O; R) nội tiếp  ABC, (O)
tiếp xúc AB, AC, BC lần lượt tại A E C D, E, F. 3) Tứ giác ADOE có    0 DAE  ADE  AED  90 0.5
 Tứ giác ADOE là hình chữ nhật Lại có OD = OE = R
Tứ giác ADOE là hình vuông  AD = OD = R
Theo tính chất của hai tiếp tuyến cắt nhau, ta có: AD = AE, BD = BF, CE = CF
 AB + AC = AD + BD + AE + CE = AD + BF + AD + CF = 2AD + BC
 AD = (AB + AC – BC) : 2 = (8 + 15 – 17) : 2 = 3(cm)  R = 3cm.
Bán kính đường tròn đáy là: C 6 r    3 (cm) 2 2 4)
Gọi  là độ dài đường sinh, h là chiều cao của hình nón 0.5
Áp dụng định lí Py-ta-go, ta có: 2 2 2 2
h    r  5  3  4 (cm) Thể tích hình nón là: 1 1 2 2 V  r  h  .  3 .4  12 (cm3) 3 3 
1   x 1 1 x  P  x  :       x  x x   x  x
 x  1 x  11 1   x  : x x  x   1
x 1 x 11  x : x x  x   1 x 1 x  x 1)  : x x  x   1 1.0 Câu 2
 x  1 x  1 x x  1 (1,5đ)  : x x  x   1  x  2 1  x  x  2 1 Vậy P 
với x  0 và x  1. x
Với x  0 và x  1, ta có:
 x  2  x  2 1 1  4 x 2) 4    x P  4 0.5 x x x
Vậy với mọi x  0 và x  1 thì P  4 . Phương trình 2 2
x  mx  m  m  4  0 2 2  1  15
c  m  m    m    1a) Ta có hệ số 4 0    2  4 0.75
 ac  0  Phương trình có hai nghiệm trái dấu
Vậy phương trình luôn có hai nghiệm phân biệt.
Vì phương trình có hai nghiệm trái dấu x  x  x  0  x 1 2 1 2
Do đó: x  x  2  x  x  2 2 1 2 1 Câu 3 1b)
Áp dụng hệ thức Vi-ét, ta có: x  x  m 0.75 (2,5đ) 1 2  m  2
Vậy m  2 là giá trị cần tìm. 2
6 x  2  3 3  x  3x 1 4 x  x  6
 6 2  x  3 3  x  3x 1 4 (2  x)(3  x) 2) ĐK: 2  x  3 1.0 Đặt 2 2
a  2  x , b  3  x (a,b  0)  3x 1  4a  b 10 Phương trình trở thành: 2 2
6a  3b  4a  b 10  4ab 2
 3(2a  b)  (2a  b) 10 2
 (2a  b)  3(2a  b) 10  0
 (2a  b  2)(2a  b  5)  0
 2a  b  5  0 (do a,b  0  2a  b  2  0)
 2a  b  5
 2 2  x  3  x  5 Cách 1:
2 2  x  3  x  5
 4(2  x)  4 (2  x)(3  x)  3  x  25
 3x 11 4 (2  x)(3  x)  25
 4 (2  x)(3  x)  14  3x 2 2
 16(6  x  x )  196  84x  9x (do x  3  14  3x  0) 2
 25x 100x 100  0 2
 x  4x  4  0 2  (x  2)  0
 x  2 (thỏa mãn ĐK)
Vậy nghiệm của phương trình đã cho là x  2 Cách 2:
Áp dụng bất đẳng thức Bunhiacopxki, ta có:
  x   x2  2 2 2 2 3
2 1 2  x  3  x  25
 2 2  x  3  x  5 Dấu “=” xảy ra 2  
x  3 x  2 x 12 4x  x  2 2 A I E F N 1 0.25 O 2 Câu 4 (3,0đ) 1 B D C
Theo tính chất của hai tiếp tuyến cắt nhau, ta có:
OB là tia phân giác của góc NOD, OE là tia phân giác của góc NOI 0.75
Mà góc NOD kề bù với góc NOI 1)
 OB  OE   BOE vuông tại O Ta có:     0 0 0 1
O  O2  DOI  BOE  180  90  90   0 1
B  O2  90 (  BOD vuông tại D)    1 O  1 B
 IOE và  DBO có:   0   OIE  ODB  90 , 1 O  1 B  IO  E # D  BO (g.g) OI EI 2    EI.BD  OI.OD  R BD OD
Chứng minh tương tự, ta được 2 FI.CD  R Vậy 2 EI.BD  FI.CD  R A I E F N K O B D P Q C 2) EI CD Từ EI.BD  FI.CD   (1) 0.5 FI BD
EF // BC (  DI ). Áp dụng hệ quả của định lí Ta-lét, ta có: EI FI  AI  EI BQ     (2) BQ CQ  AQ    FI CQ Từ (1) và (2) CD BQ CD BD CD  BD BC        1 BD  CQ BD CQ BQ CQ BQ  CQ BC
Lại có BP = CP  BP – BD = CP – CQ  PD = PQ Vì KD = KA và PD = PQ
 KP là đường trung bình của  DAQ  AQ = 2KP A C B 1 1 O O 3) 1 1.0 B S R A1 C Ta có: 1 1 1 2    AA BB CC R  OO 1 1 1 1 1 R  OO R  OO R  OO 1 1 1 1 1 1     2 AA BB CC 1 1 1 R  OO O A  OO OA AA  OA OA Lại có: 1 1 1 1 1 1 1     1 AA AA AA AA AA 1 1 1 1 1 Kẻ OR  BC, AS  BC OA OR OR.BC 2S S 1 OBC OBC      AA AS AS.BC 2S S 1 ABC ABC R  OO OA S 1 1 1 OBC   1  1 AA AA S 1 1 ABC R  OO S R  OO S Tương tự, ta có: 1 1 OAC 1 1 OAB  1 ;  1 BB S CC S 1 ABC 1 ABC R  OO R  OO R  OO  S S S  1 1 1 1 1 1 OBC OAC OAB     3      AA BB CC S S S 1 1 1  ABC ABC ABC  R  OO R  OO R  OO S 1 1 1 1 1 1 ABC     3   3 1  2 AA BB CC S 1 1 1 ABC
Dấu “=” xảy ra  O  O   ABC đều (vô lí, vì AB < AC) 1 1 1 1 2 Vậy    (đpcm). AA BB CC R  OO 1 1 1 1 1
(2x  4y 1) 2x  y 1  (4x  2y  3) x  2y  (1)  2 2
x  8x  5  2(3y  2) 4x  3y  2 2x  5x  2  (2)
Đặt u  2x  y 1 , v  x  2y u,v  0 .
Phương trình (1) trở thành: 2 2
(2v 1)u  (2u 1)v 2 2
 2uv  u  2u v  v  0
 2uv(v  u)  (v  u)  0
 (v  u)(2uv 1)  0
 v  u  0 (do u,v  0  2uv 1  0)  v  u Câu 5
 x  2y  2x  y 1 1) 0.5 (1,0đ)
 x  2y  2x  y 1
 3y  x 1
Thay 3y  x 1 vào phương trình (2) được: 2  1 
x  8x  5  2(x 1) 3x 1  2 (x  2)(2x 1) ĐK: x      3  2
 (x  2x 1)  6x  4  2(x 1) 3x 1  2 (x  2)(2x 1) 2
 (x 1)  3x 1 2(x 1) 3x 1  
 x  2  2x 1 2 (x  2)(2x 1)   0   2
 x 1 3x 12   x  2  2x 1  0
 x 1 3x 12   x  2  2x 12  0
x 1 3x 1  0
  x2  2x10
x 1  3x 1
  x2  2x1 2 x  x  0
 x2 2x1  x  1 (TMĐK)
Với x  1 thì y  0
Thử lại thấy (x, y)  (1;0) là nghiệm của hệ.
Vậy nghiệm của hệ phương trình là (x, y)  (1;0) .
Sử dụng giả thiết ab  2bc  2ca  7 và áp dụng bất đẳng thức Cô-si, ta có: 2 2 2
8a  56  2 2(a  7)  2 2(a  ab  2bc  2ca)
 2 2(a  b)(a  2c)  2(a  b)  a  2c  3a  2b  2c Tương tự: 2
8b  56  3b  2a  2c 2 2
4c  7  4c  ab  2bc  2ca  (2c  a)(2c  b) 1
 2c  a  2c  b 2 Do đó: 2 2 2
8a  56  8b  56  4c  7 1 2)
 (3a  2b  2c)  (3b  2a  2c)  (4c  a  b) 0.5 2 1
 11a 11b 12c 2 11a 11b 12   c Q  2
1 11a 11b12c 2 Dấu “=” xảy ra
2(a  b)  a  2c  b  2c a  b  1  
 2c  a  2c  b   3 c 
ab 2bc 2ca 7       2 3
Vậy min Q  2 khi a  b  1,c  . 2 Thầy Nguyễn Mạnh Tuấn
Trường THCS Cẩm Hoàng – Cẩm Giàng – Hải Dương