Đề Toán tuyển sinh lớp 10 THPT năm 2018 – 2019 sở GD và ĐT Đắk Lắk

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 TRUNG HỌC PHỔ THÔNG TỈNH ĐẮK LẮK NĂM HỌC 2018 - 2019 MÔN THI: TOÁN
(Thời gian 120 phút không kể thời gian phát đề)
ĐỀ THI CHÍNH THỨC Ngày thi 08/6/2018
Câu 1: (1,5 điểm)
1) Tìm x, biết: 2 x  3 2) Giải phương trình: 2
43x  2018x 1975  0
3) Cho hàm số y  a   2
1 x . Tìm a để hàm số nghịch biến khi x  0 và đồng biến khi x  0
Câu 2: (2,0 điểm) Cho phương trình: 2
x  m   2 2
1 x  m  2  0   1 , m là tham số.
1) Tìm m để x  2 là nghiệm của phương trình (1);
2) Xác định m để phương trình (1) có hai nghiệm phân biệt x , x thỏa mãn điều 1 2 kiện 2 2
x  x  10 . 1 2
Câu 3: (2,0 điểm)
1) Trong mặt phẳng tọa độ Oxy cho các đường thẳng có phương trình:
d : y  x  2; d : y  2  ;
d : y  k  1 x  k. 1   2   3   
Tìm k để các đường thẳng trên đồng quy.
2) Rút gọn và tìm giá trị lớn nhất của biểu thức:  1 x  2 x  x 1 A      :
x  0, x   1 1  x x x 1 x  x  1 3  
Câu 4: (3,5 điểm)
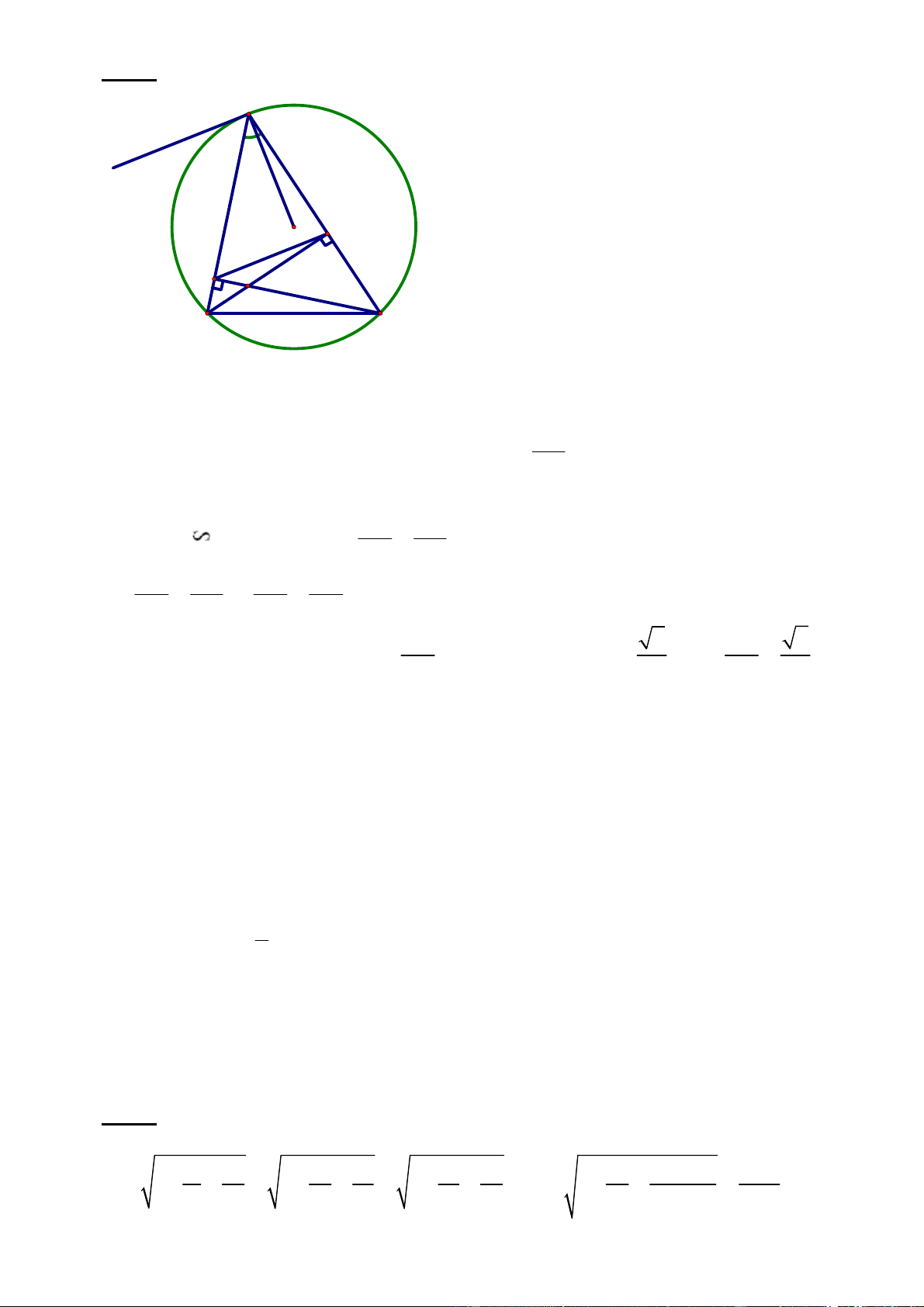
Cho tam giác ABC có ba góc nhọn và  0
A  45 . Gọi D, E lần lượt là hình chiếu
vuông góc của B, C lên AC, AB; H là giao điểm của BD và CE.
1) Chứng minh tứ giác BEDC nội tiếp. ED
2) Chứng minh: DE.AB = BC.AD và tính tỉ số . BC
3) Chứng minh: HE + HD = BE + CD.
4) Gọi I là tâm đường tròn ngoại tiếp của tam giác ABC. Chứng minh AI  DE .
Câu 5: (1,0 điểm)
Cho n là số tự nhiên khác 0. Tìm giá trị nhỏ nhất của: 1 1 1 1 1 1 1 1 101 Q  1    1    1      1    2 2 2 2 2 2 2 1 2 2 3 3 4 n n  2 1 n 1
Nguyễn Dương Hải – GV THCS Nguyễn Chí Thanh – BMT – Đăk Lăk (Sưu tầm - giới thiệu) trang 1
SƠ LƯỢC BÀI GIẢI
Câu 1: (1,5 điểm) 3 9 9
1) ĐK: x  0 . Ta có 2 x  3  x   x  (TMĐK). Vậy x  2 4 4
2) Vì a  b  c  43  2018 1975  0 . 1975
Vậy phương trình có hai nghiệm là x  1; x  1 2 43 3) Hàm số
y  a   2 1 x nghịch biến khi x  0 và đồng biến khi
x  0  a  1  0  a  1 
Câu 2: (2,0 điểm)
1) x  2 là nghiệm của phương trình (1) 2   m   2 2 2
1  2  m  2  0
 m  m    m  2 2 4 2 0 2
 2  0  m  2  2 m  2  2   0 m  2  2  0 m  2  2     m  2  2  0  m  2  2 
2) Phương trình (1) có hai nghiệm phân biệt x , x 1 2 1
   0  m  2 1   2
m  2  0  2m 1  0  m  2
x  x  2 m  1 1 2   Theo Viét, ta có:  2 x x  m  2  1 2 2 2 Khi đó 2 2
x  x  10   x  x   2x x  10  2m   1   2    2 m  2  10 1 2 1 2 1 2   m 1  0 m  1 tm 2  
 m  4m  5  0  m  
1 m  5  0     m  5  0 m  5  l   
Vậy m  1 thì PT (1) có hai nghiệm phân biệt x , x thỏa mãn điều kiện 2 2
x  x  10 . 1 2 1 2
Câu 3: (2,0 điểm)
 y  x  2 x  4 
1) Tọa độ giao điểm của d , d là nghiệm của hệ   1   2   y  2 y  2  
Do đó các đường thẳng trên đồng quy  d đi qua điểm  4  ;  2 3  2
 2  4k  
1  k  3k  2  k   3  1 x  2 x  x 1 2) A      : 1  x x x 1 x  x  1 3  
x  x   1  x  2  x  x   1 3 x  2 1 3 3    
 x  1x  x  1 x 1  x  2
1  x  x   x  x 1 1 3
Vì x  0  x 
x  1  1  A   3 x  x  1
Đẳng thức xảy ra  x  0 tmdk  . Vậy Max A  3  x  0 .
Nguyễn Dương Hải – GV THCS Nguyễn Chí Thanh – BMT – Đăk Lăk (Sưu tầm - giới thiệu) trang 2
Câu 4: (3,5 điểm) A 450 x I D E H B C
1) Chứng minh tứ giác BEDC nội tiếp.   0
BDC  BEC  90  BD  AC, CE  AB . Vậy tứ giác BEDC nội tiếp. ED
2) Chứng minh: DE.AB = BC.AD và tính tỉ số . BC 
Xét ADE và ABC, ta có: A (góc chung);  
AED  ACB (tứ giác BEDC nội tiếp) AD AB  ADE ABC (g.g)  
 DE  AB  BC.AD (đpcm) DE BC AD AB DE AD Từ    . DE BC BC AB  AD 2 DE 2 Lại có ABD: 0
ADB  90  gt   0 
 cos BAD  cos 45  . Vậy  AB 2 BC 2
3) Chứng minh: HE + HD = BE + CD.  ABD: 0 ADB   gt   0 BAD   gt   0 90 , 45  ABD  45  BEH: 0 BEH   gt    0 90
, EBH  ABD  45 cmt 
Do đó BEH vuông cân tại E  HE = BE (a)
Chứng minh tương tự có: CDH vuông cân tại D  HD = CD (b)
Từ (a), (b) suy ra HE + HD = BE + CD (đpcm)
4) Chứng minh AI  DE .
Kẻ tiếp tuyến Ax của đường tròn (I)  Ax  AI (*)   1 
và BAx  ACB 
sd AB (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn 2 
cung AB của đường tròn (I))   Lại có  
AED  ACB (tứ giác BEDC nội tiếp)  BAx  AED  Ax / / DE **
Từ *, ** suy ra AI  DE (đpcm)
Câu 5: (1,0 điểm)
Cho n là số tự nhiên khác 0. Tìm giá trị nhỏ nhất của: 1 1 1 1 1 1 1 1 101 Q  1    1    1      1    2 2 2 2 2 2 2 1 2 2 3 3 4 n n  2 1 n 1
Vì n là số tự nhiên khác 0, nên ta có:
Nguyễn Dương Hải – GV THCS Nguyễn Chí Thanh – BMT – Đăk Lăk (Sưu tầm - giới thiệu) trang 3 2 2 1 1 1 1 2  1    2 1    1     1   2     n n  2 1  n n  1 n n   1 n n   1 n n   1   2  1  1 1 1  1   1   1     . nn   1 nn   1 n n  1    1 1   1 1   1 1   1 1  101
Do đó: Q  1    1    1      1             1 2   2 3   3 4   n n 1 n 1 1 101 100  n  1    n 1  n  1 n  1 n 1 100
Vì n là số tự nhiên khác 0 nên n  1  0;
 0 . Áp dụng BĐT A  B  2 AB n  1 100
Ta có Q  2 n   1   2 100  20 n  1 100 2
Dấu “=” xảy ra  n  1   n   1
 100  n  1  10  n  9 do n 1  0 n  1
Vậy MinQ  20  n  9
Nguyễn Dương Hải – GV THCS Nguyễn Chí Thanh – BMT – Đăk Lăk (Sưu tầm - giới thiệu) trang 4