Đề Toán tuyển sinh lớp 10 THPT năm 2019 – 2020 sở GD&ĐT Thanh Hóa

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT THANH HÓA
NĂM HỌC 2019 – 2020 MÔN: TOÁN 10
(Thời gian làm bài 120 phút) Câu 1: (2.0 điểm) x  2 5 1 Cho biểu thức A   
với x  0 và x  4 x  3 x  x  6 x  2 1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x  6  4 2 Câu 2: (2,0 điểm)
1. Cho đường thẳng d  : y  ax  b . Tìm a,b đế đường thẳng d  song song với đường thẳng
d: y  5x  6 và đi qua điểm A2;3 . 3
 x  2y 11
2. Giải hệ phương trình  .
x  2y  5 Câu 3: (2.0 điểm)
1. Giải phương trình 2
x  4x  3  0 .
2. Cho phương trình 2
x  2m  
1 x  2m  5  0 ( m là tham số). Chứng minh rằng phương
trình luôn có hai nghiệm phân biệt x , x với mọi m . Tìm m để các nghiệm đó thỏa mãn hệ 1 2 thức:  2
x  2mx  x  2m  3 2
x  2mx  x  2m  3  19 1 1 2 2 2 2  Câu 4: (3,0 điểm)
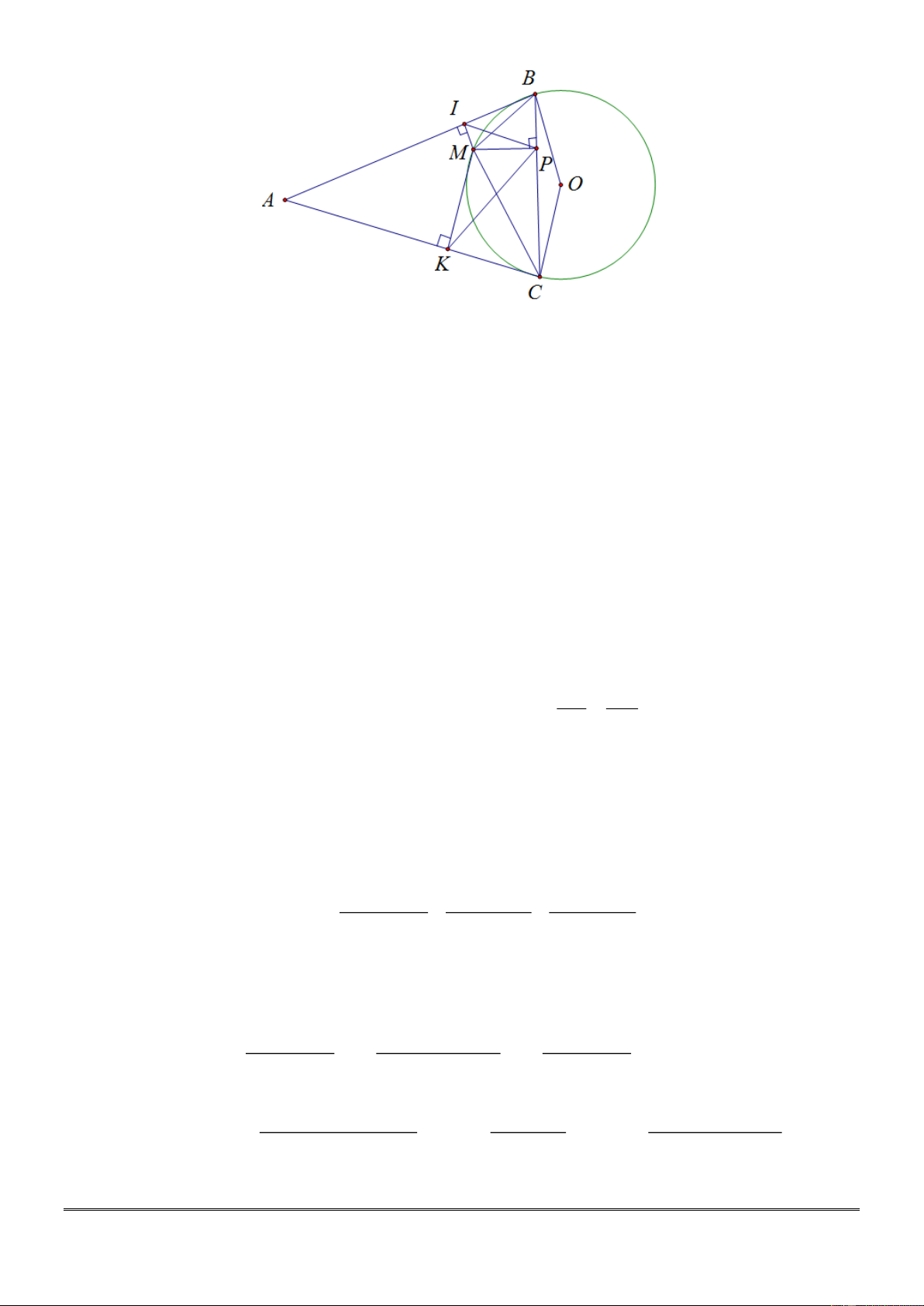
Từ một điểm A nằm ngoài đường tròn tâm O bán kính R , kẻ các tiếp tuyến A , B AC với
đường tròn ( B,C là tiếp điểm). Trên cung nhỏ BC lấy một điểm M bất kỳ khác B và C . Gọi
I , K, P lần lượt là hình chiếu vuông góc của điểm M trên các đường thẳng AB, AC, BC .
1. Chứng minh rằng AIMK là tứ giác nội tiếp.
2. Chứng minh MPK  MBC .
3. Xác định vị trí điểm M trên cung nhỏ BC để tích MI.MK.MP đạt giá trị nhỏ nhất. Câu 5:
Cho các số thực dương a, ,
b c thỏa mãn abc  1. Chứng minh rằng ab bc ca   1 4 4 4 4 4 4
a  b  ab
b  c  bc
c  a  ca
-------------- HẾT -------------- Trang 1/5
ĐÁP ÁN THAM KHẢO MÔN TOÁN
ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2019 – 2020
SỞ GD&ĐT THANH HÓA Câu 1: (2,0 điểm) x  2 5 1 Cho biểu thức A   
với x  0 và x  4 x  3 x  x  6 x  2 1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x  6  4 2 Lời giải 1. Rút gọn biểu thức A.
Với x  0 và x  4 x  2 5 1 x  2 5 1 Ta có: A       x  3 x  x  6 x  2 x  3
 x 3 x 2 x 2 x  4 5 x  3    
x  3 x  2  x  3 x  2  x  3 x  2
x  4  5  x  3 x  x 12 x  4    
x  3 x  2  x  3 x  2 x  2 x  4
Vậy Với x  0 và x  4 thì A= x  2
2. Tính giá trị của A khi x  6  4 2
Với x  6  4 2 ( Thỏa mãn ĐKXĐ) 2 2 x  6  4 2 2
 2  2.2. 2   2  2 2 Suy ra 2
x  (2  2)  2  2 x  4 2  2  4 2  2
Thay x = 2  2 vào biểu thức A= ta được A   1 2 x  2 2  2  2 2
Vậy với x  6  4 2 thì A  1 2 . Câu 2: (2,0 điểm)
1. Cho đường thẳng d  : y  ax  b . Tìm a,b đế đường thẳng d  song song với đường thẳng
d: y  5x  6 và đi qua điểm A2;3 . 3
 x  2y 11
2. Giải hệ phương trình  .
x  2y  5 Lời giải
1. Đường thẳng d  song song với đường thẳng d : y  5x  6 suy ra a  5 ; Trang 2/5
Vì d  đi qua điểm A2;3 suy ra 3  5.2  b  b  7  .
Kết luận a  5, b  7  . 3
 x  2y 11 3
 x  2y 11 x  3 x  3 2.        .
x  2y  5 2x  6 9   2y 11 y 1 Câu 3: (2.0 điểm)
1. Giải phương trình 2
x  4x  3  0 .
2. Cho phương trình 2
x  2m  
1 x  2m  5  0 ( m là tham số). Chứng minh rằng phương
trình luôn có hai nghiệm phân biệt x , x với mọi m . Tìm m để các nghiệm đó thỏa mãn hệ 1 2 thức:  2
x  2mx  x  2m  3 2
x  2mx  x  2m  3  19 1 1 2 2 2 2  Lời giải
1. Phương trình bậc hai có dạng đặc biệt a  b  c  0 nên có hai nghiệm x 1 và x  3
2. Ta có   m  2 2
1  2m  5  m  4m  6  m  2 2  2  0
Do đó phương trình đã cho luôn có hai nghiệm phân biệt x , x với mọi giá trị của tham số m 1 2 Dễ thấy 2
x  m   x  m     2 2 1 2 5 0
x  2mx  2m  3  2x  2  0 Vì x , x
là hai nghiệm của phương trình đã cho nên ta có 2
x  2mx  2m  3  2  2x và 1 2 1 1 1 2
x  2mx  2m  3  2  2x 2 2 2 Do đó  2
x  2mx  x  2m  3 2
x  2mx  x  2m  3  19 1 1 2 2 2 2    2 2  2x  x
2  2x  x  19  2  x  x
 6 x  x  x x  15 . 1 2   1 2  1 2   2 1  1 2
x  x  2 m 1 1 2  
Áp dụng định lý Viet ta có x x  2m5  1 2 m  0 2  Ta có 8m   1 12 m  
1  2m  5  15 2
 8m  26m  0  13 m   4
Có 2 giá trị của m thỏa mãn yêu cầu. Câu 4: (3,0 điểm)
Từ một điểm A nằm ngoài đường tròn tâm O bán kính R , kẻ các tiếp tuyến A , B AC với
đường tròn ( B,C là tiếp điểm). Trên cung nhỏ BC lấy một điểm M bất kỳ khác B và C . Gọi
I , K, P lần lượt là hình chiếu vuông góc của điểm M trên các đường thẳng AB, AC, BC .
1. Chứng minh rằng AIMK là tứ giác nội tiếp.
2. Chứng minh MPK  MBC .
3. Xác định vị trí điểm M trên cung nhỏ BC để tích MI.MK.MP đạt giá trị nhỏ nhất. Lời giải Trang 3/5
1. Chứng minh rằng AIMK là tứ giác nội tiếp.
Tứ giá AIMK có các góc AIM  AKM  90 nên là tứ giác nội tiếp
2. Chứng minh MPK  MBC .
IMPB là tứ giác nội tiếp suy ra MIP  MBP (cùng chắn cung MP )
Mà MCK  MBP (cùng chắn cung MC )
MKCP là tứ giác nội tiếp suy ra MCK  MPK (cùng chắn cung MK )
Suy ra MCK  MPK (1)
Tương tự ta có MPI  MKP (2) Suy ra I  MP và P
 MK đồng dạng, do đó ta có MPK  MIP
Do đó MBP  MPK .
3. Xác định vị trí điểm M trên cung nhỏ BC để tích MI.MK.MP đạt giá trị nhỏ nhất. Hai tam giác I  MP và P
 MK đồng dạng, do đó ta có IM MP  MP MK Suy ra 2
IM .MK  MP 3
 MI.MK.MP  MP
Để MI.MK.MP đạt giá trị lớn nhất khi và chỉ khi MP lớn nhất, nên M là điểm chính giữa cung nhỏ . BC Câu 5: (1,0 điểm)
Cho các số thực dương a, ,
b c thỏa mãn abc  1. Chứng minh rằng ab bc ca   1 4 4 4 4 4 4
a  b  ab
b  c  bc
c  a  ca Lời giải Áp dụng bổ đề 4 4    2 2 a b
ab a  b  ta có ab ab 1 Ta có A       4 4
a  b  ab ab  2 2
a  b  ab 2 2
a  b  ab 2 2
a  b 1  2 2 a  b  2 2    a  b 
a b2 a b2    1     1  2 2 2 2 a  b  1  a  b 1   2   2 2 a  b   1   Trang 4/5  2 2
a  b2  a  b2
a b a b Ta đi chứng minh   hay   4 . 2 2 2 2 a  b   1  2 2 a  b   1 Vì vai trò của a, ,
b c như nhau nên giả sử a  b  c a b
a b b  cc  a 2 2  4 
a b  c2    2 2 a  b 1 2  2 2 2
a  b  c   3 2  2 2 2
a  b  c   3 a b2 bc2 c a2 a b2 bc2 a c2
a bbc a c       2 2 2 2 2 2 2 2 2 2 2 2 a  b  b  c  c  a  a  b  b  c  c  a   2 2 2 1 1 1 1 1 1
2 a  b  c   3 4a  c2  . 2 2 2 2
a  b  c   3
4a  b  c2 4a  c2 Ta cần chứng minh   . 2 4 2 2 2
a  b  c   3 2 2 2 2
a  b  c   3
 a  b  c2  a  c2   2 2 2
2 a  b  c   3 Mặt khác 3 2 2 2
ab  bc  ca  3 a b c  3 Ta đi chứ 2 2
ng minh a  b  c  a  c   2 2 2
2 a  b  c   ab  bc  ca 2 2 2
 a  b  c  ab  bc  ca 2 2
 a  ac  c   2 2 2 2 2
2 a  b  c   ab  bc  ca 2  b
  ab  bc  ac  0
 ba b  ca b  0
 a  bb  c  0 luôn đúng. Ta được điều phải chứng minh.
-------------- HẾT -------------- Trang 5/5