Đề Toán tuyển sinh vào lớp 10 THPT 2018 – 2019 sở GD và ĐT Bắc Giang

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH LỚP 10 THPT BẮC GIANG NĂM HỌC 2018-2019 Môn thi : Toán
Thời gian : 120 phút không kể thời gian giao đề ĐỀ THI CHÍNH THỨC
Ngày thi 6 tháng 6 năm 2018 Câu 1. (2 điểm)
1.Tính giá trị biểu thức A  5  20  51
2 .Tìm tham số m để đường thẳng y = (m-1)x +2018 có hệ số góc bằng 3.
Câu 2: (3 điểm) x4y8
1.Giải hệ pt: 2x5y 13     a  a    2 1 6 10 2
2.Rút gọn biểu thức: B       với a > 0,a1 a 1 
a a  a  a 1 4 a a)Rút gọn biểu thức B.
b)Đặt C  B.a  a   1 . So sánh A với 1. 3. Cho pt: 2
x  (m  2)x  3m  3  0 (1)
(với x là ẩn m là tham số) a)Giải pt (1) khi m = -1 .
b)Tìm các giá trị của m để Pt (1) có hai nghiệm phân biệt x , x sao cho x , x là độ dài 1 2 1 2
hai cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng 5. Câu 3: (1,5 điểm)
Bạn Linh đi xe đạp từ nhà đến trường với quãng đường 10km. Khi đi từ trường về nhà,
vẫn trên con đường ấy, do lượng xe giao thông tham gia nhiều hơn nên bạn Linh phải giảm vận
tốc 2km/h so với khi đến trường. Vì vậy thời gian về nhà nhiều hơn thời gian đến trường là 15
phút. Tính vận tốc xe đạp khi bạn Linh đi từ nhà đến trường.
Câu 4: (3 điểm)
Cho tam giác ABC nhọn. Đường tròn tâm O đường kính BC cắt các cạnh AB, AC lần lượt
tại các điểm M, N ( M  B, N  C ). Gọi H là giao điểm của BN và CM; P là giao điểm can AH và BC.
1.Chứng minh tứ giác AMHN là tứ giác nội tiếp. 2.Chứng minh BM.BA = BP.BC
3.Trong trường hợp đặc biệt khi tam giác ABC đều canh bằng 2a. Tính chu vi đường tròn
ngoại tiếp tứ giác AMHN theo a.
4. Từ điểm A kẻ các tiếp tuyến AE và AF can đường tròn (O) đường kính BC (E, F là các
tiếp điểm). Chứng minh ba điểm E, H, F thẳng hàng. Câu 5: (0,5điểm) 2
81x  18225 x  1 6 x  8
Tìm giá trị nhỏ nhất của biểu thức: P   với x > 0 9 x x  1
HƯỚNG DẪN CHẤM (Học sinh tham khảo) Câu Ý Nội dung Điểm 1 1
A  5  20  51
A  5. 20  52 1 0,25đ 0,25đ A  100 5 1 A  10 5 1 0,25đ A  6 Vậy A = 6 0,25đ 2
Để đường thẳng y = (m-1)x+2018 có hệ số góc bằng 3 thì m-1 = 3 0,5đ  m  3 1  m  4 0,25đ
Vậy m = 4 thì Để đường thẳng y = (m-1)x+2018 có hệ số góc bằng 3 0,25đ 2 1
x  4y  8
2x 8y 16   0,25   
2x 5y 13
2x 5y 13   3  y  3 y  1 y  1      0,25 2x  5y  13 2x  5.1  13 x  4   
Vậy hệ phương trình đã cho có nghiệm duy nhất (x; y) = (4; 1) 0,25
2a Với a > 0, a  1 ta có:     a 2        a a a  2 1 1 6 10 2 6 10 2 B         a 1  a a a a 1 4 a  a 1   
 a  1a 1      4 a    6  a  
1 10  2 a  a  2 1 B    0,25đ a   1 a   1 4 a  a a   2 1 4 4 B  
 a  1a 1 4 a  a  2 1 4 a   1  a a   2 1 4 4 1 B     
 a  1a 1 4 a  0,25đ a  2 1  a   4 1 a a 1 Vậy B  với a > 0, a  1 a 0,25đ 2b
a a  1 1 Ta có: C  .
B a  a   1 
a a  1  a a  a a a a a      2 1 1 2 1 Xét C 1  1   0,25đ a a a
Vì a> 0  a  0 và  a  2
1  0 với a > 0, a  1 nên C – 1 > 0  C  1 Vậy C > 1 0,25đ 3a 2
Xét Pt: x m  2 x  3m  3  0 (1)
a)Thay m = - 1 vào phương trình (1) ta được: 2
x  x  6  0 0,25    2 1  4. 6    25    5
Phương trình có hai nghiệm phân biệt 1 5 x   3 1 2 1 5 x   2 2 2
Vậy khi m = - 1 thì phương trình (1) có tập nghiệm S  3;  2 0,25 3b 2
b) x m  2 x  3m  3  0 (1)   
 m   2   m  2 2 Δ 2 4 3
3  m 8m 16  (m  4)  
Để pt (1) có hai nghiệm phân biệt     m  2 0 4
 0  m  4  0  m  4
x  x  m  2
Theo hệ thức Viet ta có 1 2
x x 3m3  1 2
Theo đề bài hai nghiệm x , x của PT (1) là độ dài 2 cạnh góc vuông của một 1 2   0 x x  0
tam giac vuông có cạnh huyền bằng 5  1 2   0,25đ x  x  0  1 2 2 2
x  x  25  1 2 m  4 m  4   m  4 3m  3  0 m  1         m  1 m  2  0 m  2    2
m  2m 15  0 (2)
x x 2 2x x 25
m 22 2 3m 3 25           1 2 1 2    
Giải PT (2) được m = 5 (Thỏa mãn); m = - 3 (không thỏa mãn)
Vậy m = 5 là giá trị cần tìm 0,25đ 3 1
Đổi 15 phút = (giờ) 4
Gọi vận tốc xe đạp khi bạn Linh đi từ nhà đến trường là x (km/h) ĐK: x >2 0,25 10
Thời gian bạn Linh đi xe đạp từ nhà đến trường là: (giờ) x
vận tốc xe đạp khi bạn Linh đi từ trường về nhà là : x-2 (km/h) 0,25 10
Thời gian bạn Linh đi xe đạp từ trường về nhà là: (giờ) x  2 1
Vì thời gian về nhà nhiều hơn thời gian đến trường là (giờ) nên ta có PT 4 10 10 1 0,25   x  2 x 4 2
 x  2x 80  0
Giải PT được x  10 (thỏa mãn) 1 0,5
x  8 (loại) 2 0,25
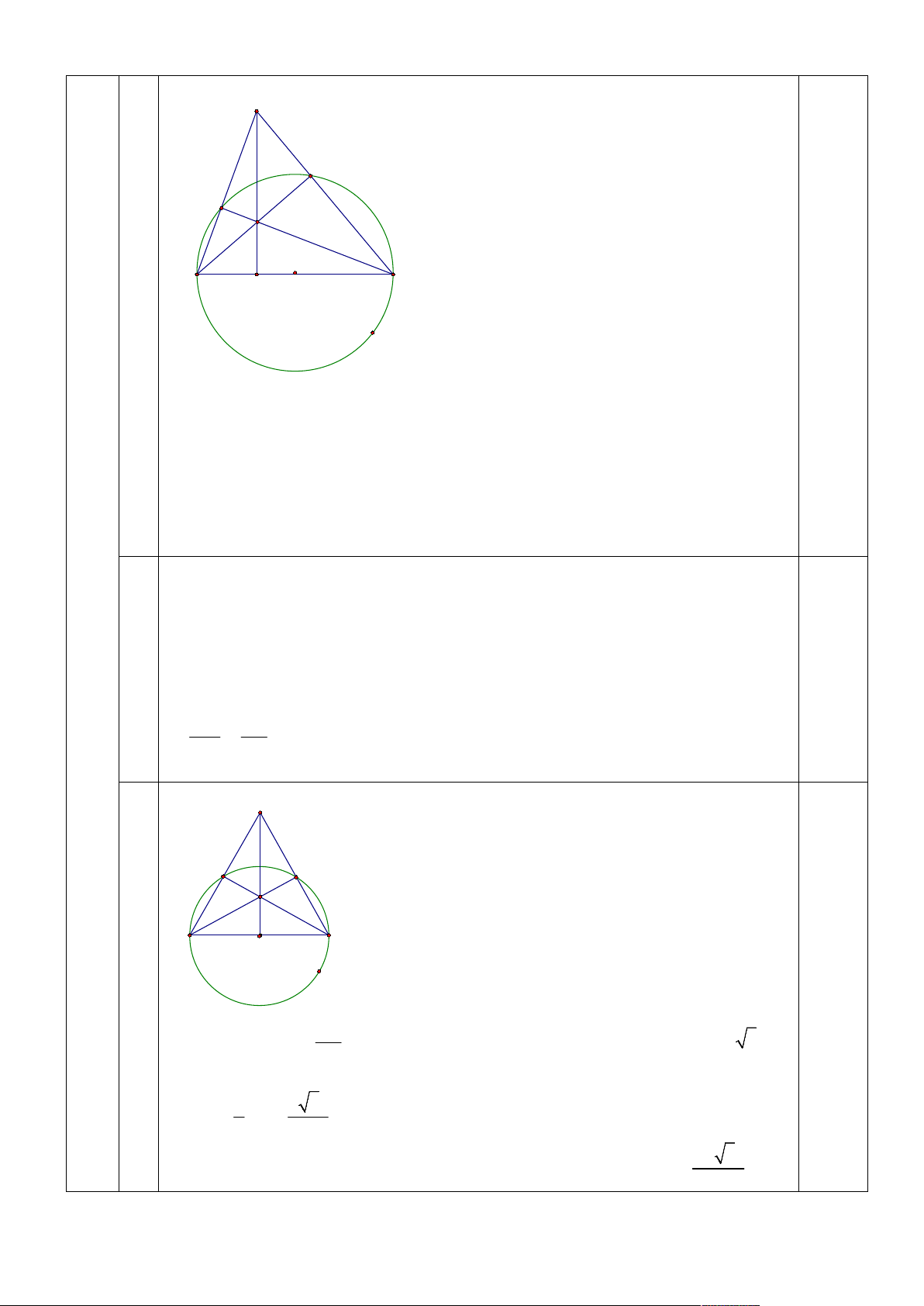
Vậy vận tốc xe đạp khi bạn Linh đi từ nhà đến trường là 10 (km/h) 4 1 A N M H B C p O
Xét đường tròn (O) có  0
BMC  90 (góc nội tiếp chắn nửa đường tròn (O))  0  AMH  90 0,25  0
BNC  90 (góc nội tiếp chắn nửa đường tròn (O))  0  ANH  90 0,25
Xét tứ giác AMHN có 0,25   0 0 0
AMH  ANH  90  90  180 ,mà hai góc này là 2 góc đối nhau
nên tứ giác AMHN là tứ giác nội tiếp 0,25 2
Chứng minh được H là trực tâm ΔABC
Suy ra AP là đường cao  0  APB  90    0
BPA  BMC  90 0,25
Xét ΔBPA và ΔBMC có  ABP là góc chung   0
BPA  BMC  90 0,25
Δ BPA ~ ΔBMC (gg) BP BA  
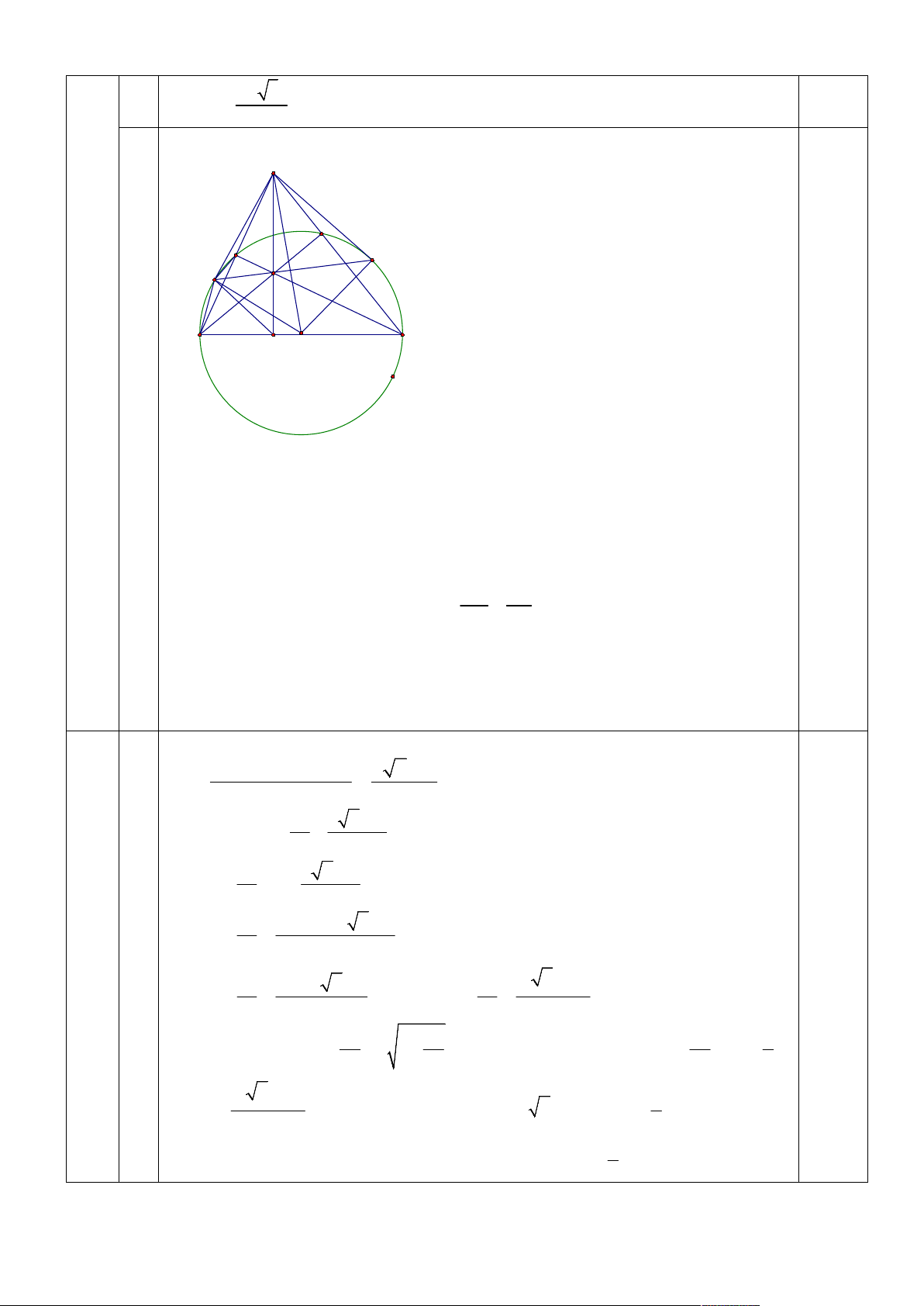
 BM .BA  B . P BC (đpcm) 0,25 BM BC 3 A M N H p B C O BC 0,25 A
 BC đều  PC   a . Tính 2 2 2 2 2 2
AP  AC  PC  4a  a  3a  AP  3a 2 A
 BC đều mà H là trực tâm A
 BC  H đồng thời là trọng tâm của A  BC 2 2 3a  AH  AP  3 3 0,25  2 3a
Chu vi đường tròn ngoại tiếp tứ giác AMHN là: C   d   .AH  0,25 3  2 3a Vậy C  3 4 A M N F E H C B p O Ta có:    0
AEO  AFO  APO  90 Suy ra 5 điểm A, E, P, O, F cùng nằm trên
một đường tròn. Mà AE = AF (tính chất 2 tiếp tuyến cắt nhau)    AE  AF Do đó  
AEF  APE (do 2 góc nội tiếp chắn 2 cung bằng nhau)(1) 0,25
Chứng minh Δ AEM ~ ΔABE (gg) 2
 AE  AM.AB (2)
Chứng minh Δ AMH ~ ΔAPB (gg)  AM.AB  AH.AP (3) AE AP
Từ (2) và (3) suy ra 2
AE  AH.AP  
 Δ AEH ~ ΔAPE (c.g.c) AH AE Từ đó suy ra   AEH  APE (4)
Từ (3) và (4) suy ra  
AEH  AEF  3 điểm E, H, F cùng nằm trên tia EF. Do 0,25
đó 3 điểm E, H, F thẳng hàng. 5 Ta có: 2
81x  18225 x  1 6 x  8 P   với x > 0 9 x x  1 1 6 x  8
P  9x  2025   9x x 1 1 6 x  8 P  9x  9  2016 9x x 1 1
9x  9  6 x 8 P  9x    2016 9x x 1  x x x    2 3 1 1 9 6 1 1 P  9x    2016  9x    2016 9x x 1 9x x 1 0,25 1 1 1 1 Theo BĐT cô si 9x   2 9x.
 2 Dấu bằng xảy ra khi 9x   x  9x 9x 9x 9  x  2 3 1 1 Ta có:
 0 Dấu bằng xảy ra khi 3 x 1  0  x  x 1 9 1
Do đó P  2  0  2016  2018 . Dấu bằng xảy ra khi x  (thỏa mãn) 9 1
Vậy minP = 2018 khi x  9 0,25