ĐỀ TƯ DUY TOÁN HỌC TSA SỐ 03

ĐỀ TƯ DUY TOÁN HỌC TSA SỐ 03
TSA 1: [ILP] Xét tính chẵn lẻ của 3 hàm số sau đây:
| x −1| − | x +1| f (x) = −x 2 g( )
x = x (| x +1| − | x −1|) 3
h(x) = x − x +1
Khẳng định nào sau đây đúng?
A. f và g là hàm số lẻ
B. g và h là hàm số lẻ
C. f là hàm số chẵn
D. g là hàm số chẵn
TSA 2: [ILP] Tập hợp các giá trị của tham số m để hàm số 2
y = 2x + 2mx − 2m +1 đồng biến trên
khoảng (3; +∞) là: A. [−3; +∞). B. [−6; +∞). C. (−∞; −6]. D. (−∞; −3].
TSA 3: [ILP] Có bao nhiêu giá trị nguyên âm của tham số m để hàm số sau xác định x  R : 2 f
= (m + 4)x − (m − 4)x − 2m +1 ? ( x) A. 1 B. 2 C. 3 D. Vô số TSA 4: [ILP] Cho 2
f (x) = mx − 2mx + 4 . Tập hợp tất cả các giá trị của tham số m để f ( ) x  0, x   là: A. (− ;  0) (4;+ )  . B. (0; 4) . C. (− ;  0][4;+ )  . D. [0; 4) . 2 x − 4x + 3
TSA 5: [ILP] Số nghiệm nguyên của bất phương trình  0 2 x − là: 16 A. Vô số. B. 0. C. 6. D. 8.
TSA 6: [ILP] Tìm m để phương trình 2
x − 2x + m = 2x +1 có nghiệm? A. m < −3 B. m > −2 C. m ≥ 1 D. m = 5
TSA 7: [ILP] Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? NHẬN ĐỊNH ĐÚNG SAI Hàm số x y = 3sin
tuần hoàn với chu kì π. 2
Tập giá trị của hàm số y = 3 sin x − cos x − 2 là [−4;0].
TSA 8: [ILP] Cho dãy số u = = +  n xác định bởi: u 1, u 2u 3 (n
2) . Các khẳng định sau là đúng hay 1 n 1 + n sai? NHẬN ĐỊNH ĐÚNG SAI
un lập thành cấp số nhân.
Số hạng tổng quát của dãy là 2n+1 − 3
TSA 9: [ILP] Một chiếc guồng nước có dạng hình tròn bán kính 2,5m; trục của nó đặt cách mặt nước 2m.
Khi guồng quay đều, khoảng cách h (mét) từ một chiếc gầu gắn tại điểm A của guồng đến mặt nước   
được tính theo công thức h = |y|, trong đó 1
y = 2 + 2,5sin 2 t −  
 với t (phút) là thời gian quay của   4 
guồng. Ta quy ước y > 0 khi gầu ở trên mặt nước và y < 0 khi gầu ở dưới nước.
Điền số thích hợp vào ô trống:
Sau khi guồng nước bắt đầu quay, thời điểm đầu tiên chiếc gầu ở vị trí thấp nhất là: ______ phút.
TSA 10: [ILP] Số điểm biểu diễn nghiệm của phương trình 2 sin x − 2cos .
x sin x +1 = 0 trên đường tròn lượng giác là: A. 1 B. 0 C. 2 D. 3
TSA 11: [ILP] Khi một vận động viên nhảy dù nhảy ra khỏi máy bay, giả sử quãng đường người ấy rơi
tự do (tính theo feet) trong mỗi giây liên tiếp theo thứ tự trước khi bung dù lần lượt là: 16; 48; 80; 112;
144;… (các quãng đường này tạo thành cấp số cộng).
Khẳng định nào đúng, khẳng định nào sai? NHẬN ĐỊNH ĐÚNG SAI
Công sai của cấp số cộng trên là d = 30
Tổng chiều dài quãng đường rơi tự do của người đó trong 10 giây đầu tiên là 1060 feet n
TSA 12: [ILP] Cho dãy số (a có a = , n
  *. Tìm số hạng lớn nhất của dãy số (a . n ) n ) n 2 n +100 1 1 1 1 A. . B. . C. . D. . 20 30 25 21
TSA 13: [ILP] Cho cấp số cộng un = 5n − 1. Tính A = u26 + u27 + ... + u100? A. 23550. B. 26750. C. 25150. D. 1600
TSA 14: [ILP] Bốn góc lượng giác có số đo dương lập thành 1 cấp số nhân có tổng là 360∘. Tìm số đo
góc lớn nhất, biết rằng số đo của góc đó gấp 8 lần số đo của góc nhỏ nhất: A. 24⁰ B. 192⁰ C. 48⁰ D. 90⁰
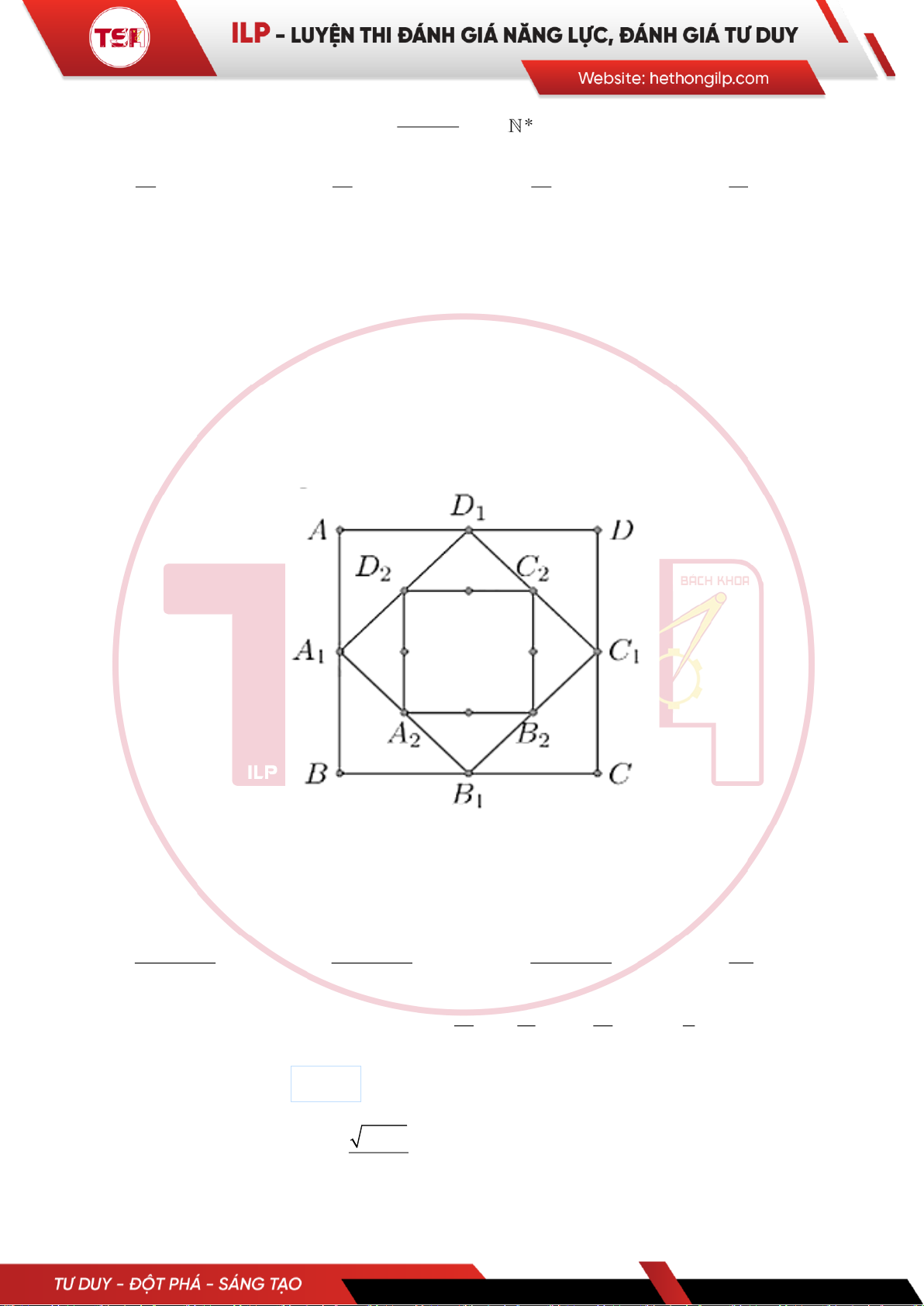
TSA 15: [ILP] Cho hình vuông ABCD có các cạnh bằng a và có diện tích bằng S1. Nối bốn trung
điểm A1, B1, C1, D1 theo thứ tự của bốn cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích S2.
Tiếp tục quá trình trên ta được hình vuông thứ ba là A2B2C2D2 có diện tích S3 … và cứ tiếp tục như thế
ta được các hình vuông lần lượt có diện tích S4, S5, ..., S50 (tham khảo hình vẽ).
Tổng S = S1 + S2 + ... + S50 bằng: 2 a ( 50 2 − ) 1 2 a ( 50 2 − ) 1 2 a ( 49 2 − ) 1 2 a A. B. C. D. 49 2 50 2 48 2 50 2  1  1   1 
TSA 16: [ILP] Giá trị của giới hạn L = lim 1− 1− ... 1−    
 bằng a (phân số tối giản). 2 2 2  2  3   n  b
Khi đó, tổng a + b bằng ______ . 2 x + 2
TSA 17: [ILP] Tính giới hạn lim : x→− x A. +∞ B. −∞ C. 1 D. −1
TSA 18: [ILP] Cho hàm số y = |x − 1|. Chọn phát biểu đúng?
A. Hàm số liên tục và có đạo hàm tại x = 1
B. Hàm số liên tục tại x = 1 nhưng không có đạo hàm tại x = 1
C. Hàm số có đạo hàm tại x = 1 nhưng không liên tục tại đó
D. Hàm số không liên tục và không có đạo hàm tại x = 1
TSA 19: [ILP] Biết hàm số 3 2
f (x) = ax + bx + cx + d(a  0) có đạo hàm là f '( ) x  0 với x   . Mệnh đề nào sau đây đúng? A. 2
b − 3ac  0 B. 2
b − 3ac  0 C. 2
b − 3ac  0 D. 2
b − 3ac  0 1
TSA 20: [ILP] Một vật rơi tự do theo phương thẳng đứng có quãng đường dịch chuyển 2 S (t) = gt , 3
với t là thời gian tính bằng giây (s) kể từ lúc vật bắt đầu rơi, S là quãng đường tính bằng mét (m). Vận
tốc tức thời của vật tại thời điểm t = 6 s là bao nhiêu? (g = 9,8 m/s2). A. 39,2 m/s. B. 19,6 m/s. C. 156,8 m/s. D. 78,4 m/s.
TSA 21: [ILP] A, B, C, D, E, F cùng đi xem phim. 6 bạn mua được 3 vé chẵn, 3 vé lẻ. A và F muốn
được ngồi ghế chẵn, C và D muốn được ngồi ghế lẻ. B và E không có yêu cầu gì. Các nhận định sau đúng hay sai? NHẬN ĐỊNH ĐÚNG SAI
Số cách để sắp xếp vị trí cho 6 bạn là 72 cách
B và E có thể cùng chẵn hoặc cùng lẻ
Số cách để sắp xếp vị trí cho 6 bạn là 720 cách
TSA 22: [ILP] Cho tập hợp A = {1;2;3;4;5;6}.
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? NHẬN ĐỊNH ĐÚNG SAI
Tập hợp A có 64 tập con khác rỗng.
Tập hợp A có 20 tập con có 3 phần tử.
Số tập con có 2 phần tử của A bằng số tập con có 4 phần tử của A.
TSA 23: [ILP] Cho khai triển 20 2 20 (1− 2x)
= a + a x + a x ++ a x . 0 1 2 20
Trong các khẳng định sau, khẳng định nào đúng? NHẬN ĐỊNH ĐÚNG SAI
Giá trị của a − a + a bằng 801. 0 1 2
Tổng a + a + a ++ a bằng −1. 0 1 2 20
TSA 24: [ILP] Có bao nhiêu số có 5 chữ số đôi một khác nhau và trong đó có đúng một chữ số lẻ? Đáp án: ______
TSA 25: [ILP] Cho tập hợp A = {1;2;3;4;5}. Gọi S là tập hợp tất cả các số tự nhiên có ít nhất 3 chữ số,
các chữ số đôi một khác nhau được lập thành từ các chữ số thuộc tập A. Chọn ngẫu nhiên một số từ tập
S, xác xuất để số được chọn có tổng các chữ số bằng 10 được viết dưới dạng phân số tối giản a (a, b  ). b Tổng a + b = ______
TSA 26: [ILP] Tại buổi tất niên công ty, Dương và Nguyên cùng tham gia trò chơi và giành chiến thắng.
Phần quà của hai bạn được đặt trong 1 hộp kín, gồm 6 tờ 20.000 và 4 tờ 50.000. Dương lấy trước, Nguyên
lấy sau. Xác suất để Nguyên lấy được tờ 50.000 là a/b (a/b là phân số tối giản). Tổng a + b = ______
TSA 27: [ILP] Cho hình chóp S.ABC có đáy là tam giác vuông tại A, cạnh huyền BC = 6(cm), các cạnh
bên cùng tạo với đáy một góc 600.
Kéo biểu thức trong các ô thả vào vị trí thích hợp trong các câu sau: 6 cm 6cm 16π cm2 48π cm2
Các cạnh bên của hình chóp bằng: ______
Diện tích mặt cầu ngoại tiếp hình chóp S.ABC bằng: ______
TSA 28: [ILP] Cho hình chóp S. ABCD có đáy là một hình vuông cạnh a , mặt bên (SAD) là một tam giác đều và (SA ) D ⊥ (ABC )
D . Tính chiều cao của hình chóp: 3a 2a 2a 3a A. B. C. D. 3 2 3 2
TSA 29: [ILP] Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh ,
a SA ⊥ (ABC) , góc giữa SC
và mặt phẳng (ABC) bằng 30 . Tính khoảng cách giữa hai đường thẳng SB và AC. a 3 2a a 39 a 39 A. . B. . C. . D. . 13 13 13 3
TSA 30: [ILP] Cho hình chóp S.ABCD có đáy ABCD là một hình thang với đáy AD và BC.
Biết AD = a , BC = b. Gọi I và J lần lượt là trọng tâm các tam giác SAD và SBC. Mặt phẳng (ADJ) cắt
SB, SC lần lượt tại M, N. Mặt phẳng (BCI) cắt SA, SD tại P, Q. Khẳng định nào sau đây là đúng?
A. MN song song với PQ B. MN chéo với PQ C. MN cắt với PQ D. MN trùng với PQ
TSA 31: [ILP] Cho hình chóp S. ABCD có SA vuông góc với mặt phẳng (ABCD), SA = a, đáy ABCD
là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Góc giữa hai mặt phẳng (SBC) và (SCD) bằng: A. 30⁰. B. 150⁰. C. 90⁰. D. 60⁰.
TSA 32: [ILP] Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? NHẬN ĐỊNH ĐÚNG SAI Chữ số tận cùng của 10 9 9 là 9
Số dư của 31000 khi chia cho 5 là 2
TSA 33: [ILP] Những hình nào sau đây có ít nhất hai trục đối xứng?  Hình thang cân.  Hình thoi.  Hình tam giác đều.  Hình bình hành.
TSA 34: [ILP] Tìm số tự nhiên k để dãy: k + 1, k + 2, …, k + 10 chứa nhiều số nguyên tố nhất. Khi đó: k = ______
TSA 35: [ILP] Gọi S là tập có n phần tử. Mỗi phân hoạch của S được định nghĩa là tập gồm k tập
con S , S ,, S khác rỗng của S , đôi một rời nhau và hợp của chúng là S . Tức là: 1 2 k
S = S  S  S , S  , S  S =  (i  j), i
 , j = 1;2;;k $ 1 2 k i i j
Ví dụ: Tập hợp A ={ , a }
b chỉ có 1 phân hoạch là A = {{ } a ,{ } b }. 1 Tập hợp B ={ , a , b }
c có 4 phân hoạch làCho tập C = { , a , b , c d} .
Hỏi tập C có bao nhiêu phân hoạch? A. 10 B. 13 C. 11 D. 8
TSA 36: [ILP] Bạn Hải lấy một cặp số tự nhiên phân biệt rồi tính số dư khi chia tổng lập phương của
hai số cho tổng các chữ số của số lớn trong hai số đó. Nếu làm theo đúng quy tắc của bạn Hải với cặp
số (31, 175) ta thu được kết quả bằng: A. 2 B. 5 C. 0 D. 3
TSA 37: [ILP] Khoảng 200 năm trước, hai nhà khoa học Pháp là Clô-zi-ut và Cla-pay-rông đã thấy rằng
áp suất p của hơi nước (đo bằng milimet thủy ngân, kí hiệu là mmHg) gây ra khi nó chiếm khoảng trống k
phía trên của mặt nước chứa trong một bình kín được tính theo công thức t 273 p .10 a + = , với t là nhiệt
độ ∘C của nước, a và k là hằng số. Cho biết k ≈ −2258,624 và khi nhiệt độ của nước là 100∘C thì áp suất
của hơi nước là 760mmHg. Tìm [a], với [a] có giá trị nguyên không vượt quá a:
A. [a] = 863118842.
B. [a] = 863188842.
C. [a] = 863118841.
D. [a] = 863188841.
TSA 38: [ILP] Cho phương trình 2
(2m +1) cos 2x − (3m −1)sin 2x − 3m +1 = 0 (m là tham số thực). Có
tất cả bao nhiêu giá trị nguyên của m để phương trình có đúng hai nghiệm phân biệt thuộc (−π; π). A. 2 B. 4 C. 5 D. 3 2
ax +1 − bx − 2
TSA 39: [ILP] Cho biết lim (a, b  ) 3 x 1 → x − 3x +
có kết quả là một số thực. Giá trị của biểu thức 2 2 2 a + b bằng? 45 9 A. 6 + 5 3 . B. . C. . D. 87 − 48 3 . 16 4 
TSA 40: [ILP] Cho lăng trụ đứng ABC .
D A' B 'C ' D' có đáy ABCD là hình thoi, AB = a 3, BAD = 120
Góc giữa đường thẳng AC' và mặt phẳng (ADD'A') là 30 . M là trung điểm A'D', N là trung điểm BB'
Tính khoảng cách từ N đến mặt phẳng ( C'MA ): a 6 a 3 a 6 a 3 A. B. C. D. 3 3 2 2