
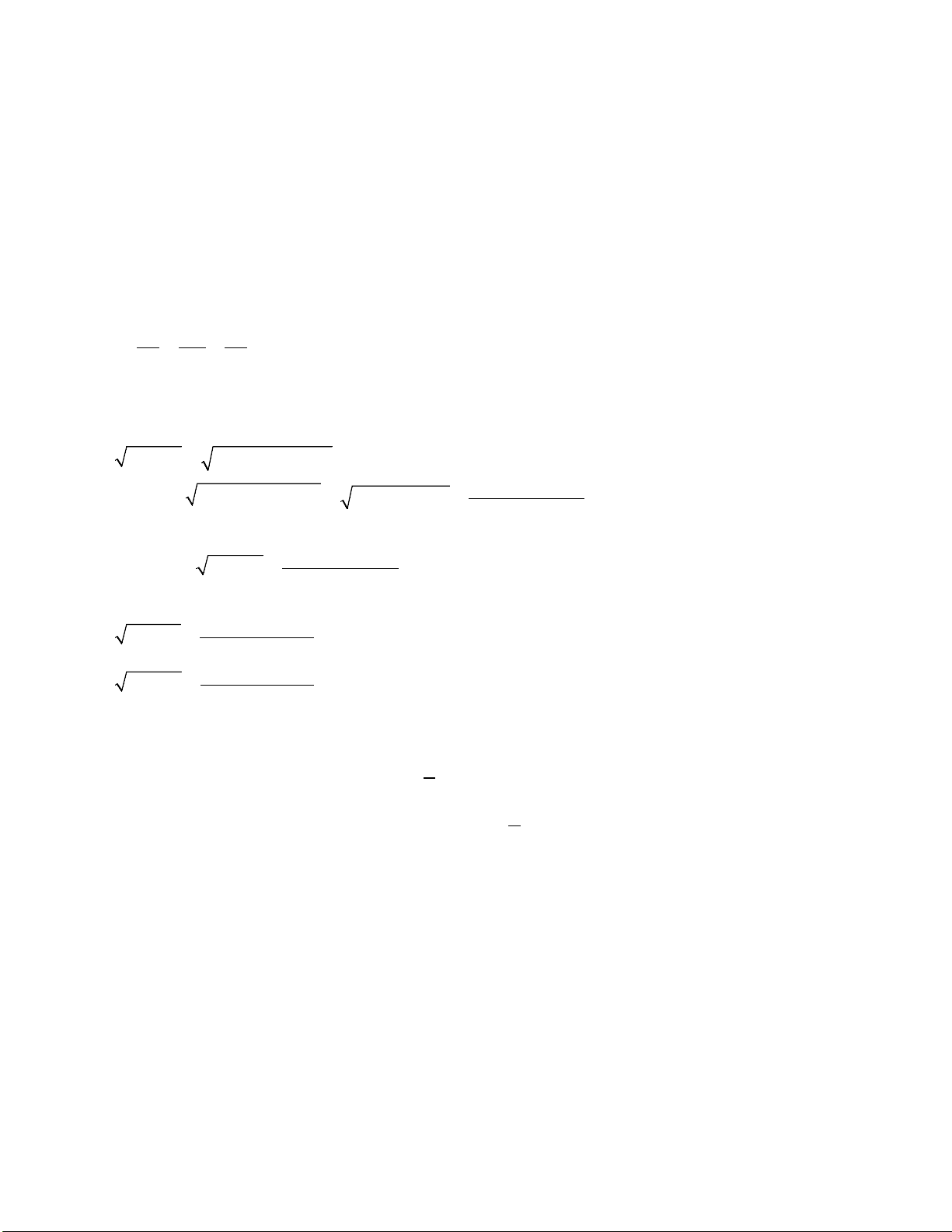
Preview text:
HƯỚNG DẪN GIẢI ĐỀ THI VÀO 10 TỈNH QUẢNG NAM Câu 1. a) 6 2 A = 18 − + (1− 2) . 3 = 3 2 − 2 + 3− 2 2 = 3.
b) Với x > 0 ta có: x − 4 x + 2 x + x − x x + = + x B ( 2)( 2) ( 2) = +
= x − 2 + x + 2 = 2 x. x + 2 x x + 2 x Câu 2.
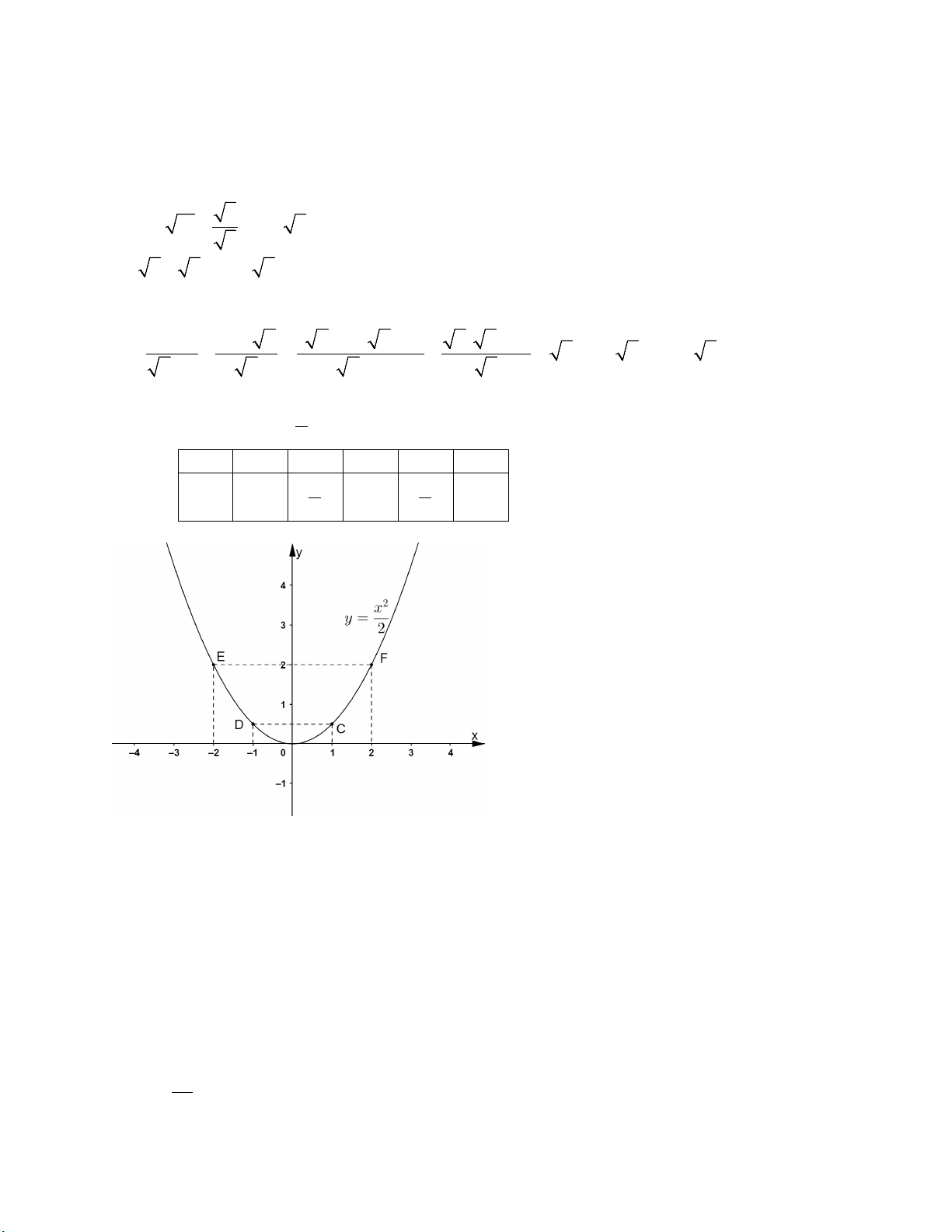
a) Vẽ đồ thị hàm số 1 2 y = x 2 x 2 − 1 − 0 1 2 y 2 1 0 1 2 2 2 b) 3 x − y = 7 9
x − 3y = 21 11 x = 33 x = 3 ⇔ ⇔ ⇔ 2x 3y 12 2x 3y 12 2x 3y 12 + = + = + = y = 2
Vậy hệ phương trình có nghiệm ( ; x y) = (3;2) . Câu 3. a) Đặt 2
x = t (t ≥ 0) , ta có: 2
2t − t −1 = 0
⇔ (t −1)(2t +1) = 0 t =1 (TM ) ⇔ 1 − t = (L) 2 x = 1 Với t =1 ⇔ x = 1 −
Vậy phương trình có tập nghiệm S = {1;− } 1 .
b) Để phương trình đã cho có hai nghiệm phân biệt thì: 2 2
∆ ' = m − (m + m − 3) = 3− m > 0 ⇔ m < 3
x + x = 2m Hệ thức Vi-et: 1 2 2
x x = m + m − 3 1 2
Ta có: x − x = m ⇒ m ≥ 0 (Vì x − x ≥ 0 ). Vậy 0 ≤ m < 3 1 2 1 2 ⇔ ( x − x )2 2 2 2 2
= m ⇔ x + x − 2x x = m ⇔ (x + x )2 2
− 4x x = m (1) 1 2 1 2 1 2 1 2 1 2
Thay hệ thức Vi-et vào (1) ta có: ( m)2 − ( 2 m + m − ) 2 2 4 3 − m = 0 2 2 2
⇔ 4m − 4m − 4m +12 − m = 0
⇔ (m + 6)(m − 2) = 0 m = 6 − (L) ⇔ m = 2 (TM ) Vậy m = 2 . Câu 4. a) Ta có:
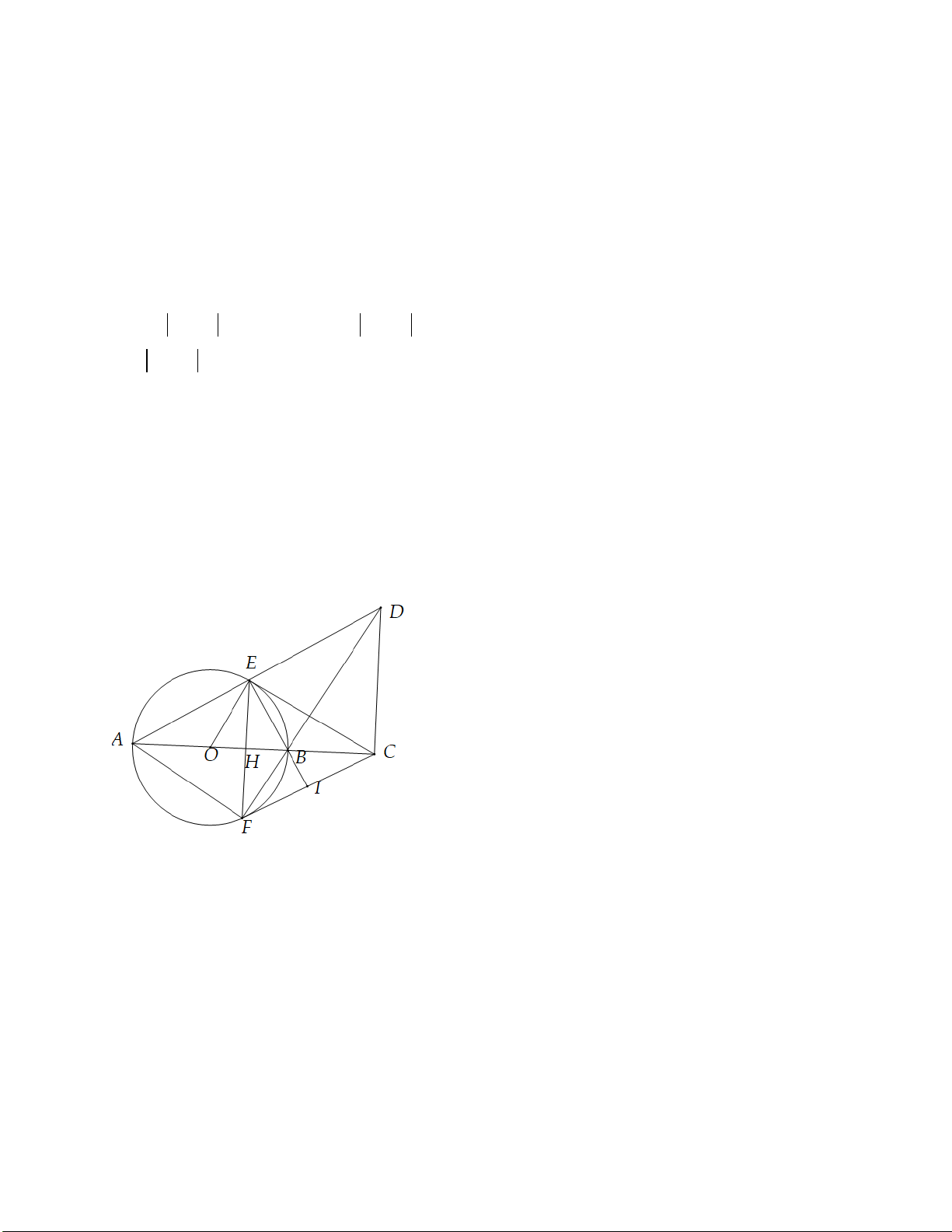
AEB = 90° (Góc nội tiếp chắn nửa đường tròn) ⇒ DEB = 90° mà DCB = 90° (Giả thiết)
Suy ra tứ giác BCDE nội tiếp. b) Ta có: BEC =
BDC (Vì tứ giác BCDE nội tiếp) Mặt khác: EFB =
BEC (Góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung) Suy ra EFB =
BDC , mà hai góc này ở vị trí so le trong nên EF / /DC hay EF / /d . EF / /CD c) Ta có:
⇒ EF ⊥ AB tại H AB ⊥ CD
⇒ H là trung điểm EF (Quan hệ vuông góc giữa đường kính và dây)
∆BFE có BH vừa là đường cao vừa là đường trung tuyến nên ∆BFE cân tại B Suy ra: FEB = BFE (1)
∆CEF có CH là đường cao đồng thời là đường trung tuyến nên ∆CEF cân tại C (dhnb) ⇒ CEF = CFE mà EFB = BEC (cmt) (2) Từ (1) và (2) suy ra BFI = FEB = FEB = BEC
Xét ∆IEF và ∆IFB có: FIE chung BFI = FEB (cmt)
Vậy ∆IEF đồng dạng với ∆IFB (g-g)
⇒ IE = FE = IF IF FB IB Mặt khác: FEB = BEC (cmt) suy ra Câu 5. Ta có:
2a + bc = (a + b + c)a + bc (Do a + b + c = 2 ) 2 ( + ) + ( + ) = + + + = ( + )( + ) ≤ a b a c a ab bc ac a b a c
(Áp dụng bất đẳng thức với hai 2
số dương a + b và a + c ) Vậy ta có: ( + ) + ( + ) 2 + ≤ a b a c a bc (1) 2 Tương tự: ( + )+( + ) 2 + ≤ a b b c b ca (2) 2 ( + ) + ( + ) 2 + ≤ a c b c c ab (3) 2
Cộng (1), (2) và (3) theo vế ta được:
Q ≤ 2(a + b + c) = 4
Dấu “=” xảy ra khi và chỉ khi 2
a = b = c = 3
Suy ra giá trị lớn nhất của Q bằng 4 khi 2
a = b = c = . 3
_____ THCS.TOANMATH.com _____
Document Outline
- de-tuyen-sinh-lop-10-chuyen-mon-toan-chung-nam-2022-2023-so-gddt-quang-nam
- 41. QUẢNG NAM




