Đề tuyển sinh lớp 10 chuyên môn Toán (chung) năm 2023 – 2024 sở GD&ĐT Hà Nam

UBND TỈNH HÀ NAM
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2023 - 2024
Môn: Toán (Đề chung) ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút, không kể thời gian giao đề
(Đề thi gồm 01 trang)
Câu I. (2,0 điểm)
1. Rút gọn biểu thức A = 2 3 − 3 27 + 7 7 + 4 3. 2. Cho biểu thức 1 1 x P = − +
(với x ≥ 0, x ≠ 4 ).
2 x − 4 2 x + 4 x − 4 a) Rút gọn biểu thức . P
b) Tìm tất cả các số nguyên x để P đạt giá trị nguyên.
Câu II. (1,5 điểm) 1. Giải phương trình 2
x + 2x −15 = 0.
x(4 − 2y) = 7 + y − 2xy
2. Giải hệ phương trình   x − =  ( y − ) . 2 14 2 3
Câu III. (1,5 điểm) Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình 2 y = x ,
đường thẳng (d) có phương trình 2
y = 2x + m − 4m + 9 (với m là tham số) và đường thẳng
(∆) có phương trình y = (a −3)x + 4 (với a là tham số).
1. Tìm a để đường thẳng (d) và đường thẳng (∆) vuông góc với nhau.
2. Chứng minh đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt , A B với
mọi m . Gọi A(x ; y ,B x ; y (với x < x ), tìm tất cả các giá trị của tham số m sao cho 1 1 ) ( 2 2) 1 2
x − 2023 − x + 2023 = y + y − 48. 1 2 1 2
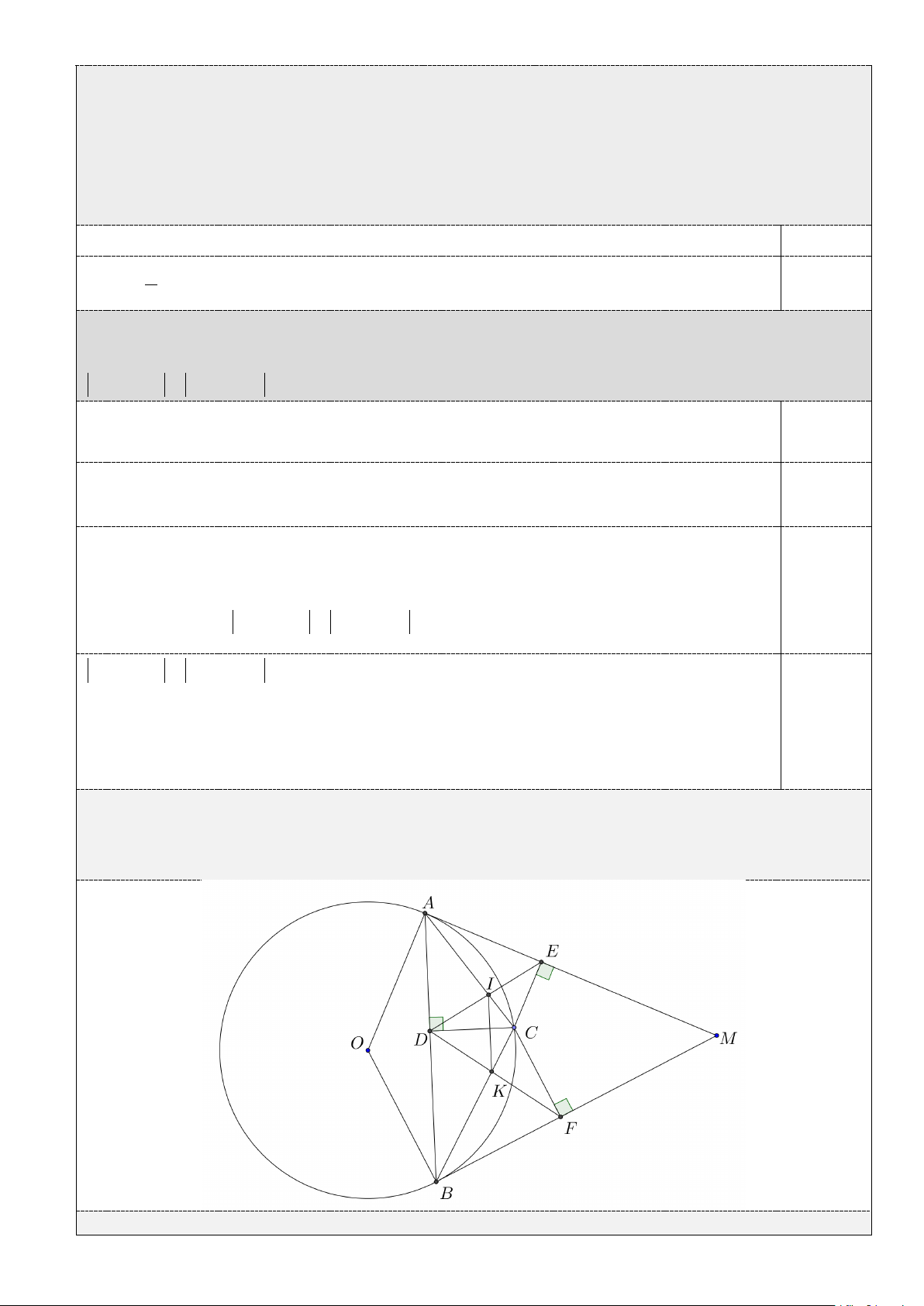
Câu IV. (4,0 điểm) Cho đường tròn (O) . Từ điểm M bên ngoài đường tròn kẻ hai tiếp tuyến ,
MA MB với đường tròn (O) ( ,
A B là các tiếp điểm). Lấy điểm C trên cung nhỏ AB
(C không nằm chính giữa cung AB , C khác A và B ). Gọi D, E, F lần lượt là hình chiếu
vuông góc của C trên các đường thẳng AB, AM , BM .
1. Chứng minh tứ giác AECD nội tiếp đường tròn.
2. Chứng minh rằng  =  CDE C . FD
3. Gọi I là giao điểm của AC và ED , K là giao điểm của CB và DF . Chứng minh CD ⊥ IK.
4. Đường tròn ngoại tiếp hai tam giác CIE và CKF cắt nhau tại điểm thứ hai N ( N
khác C ). Chứng minh đường thẳng NC đi qua trung điểm của đoạn thẳng AB .
Câu V. (1,0 điểm) Cho a,b,c là các số không âm thỏa mãn a + b + c =1011. Chứng minh: (b − c)2 (c − a)2 (a −b)2 2022a + + 2022b + + 2022c + ≤ 2022 2. 2 2 2 --- HẾT---
Thí sinh được sử dụng máy tính bỏ túi không có chức năng soạn thảo văn bản và
không có thẻ nhớ.
Họ và tên thí sinh:…………………………………...Số báo danh:...................................
Cán bộ coi thi số 1…………………………......Cán bộ coi thi số 2……………................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN HÀ NAM Năm học: 2023-2024
(Hướng dẫn chấm thi có 04 trang) ĐỀ CHÍNH TH ỨC
HƯỚNG DẪN CHẤM MÔN TOÁN (ĐỀ CHUNG) Ghi chú:
- Điểm toàn bài không làm tròn.
- Các cách giải khác mà đúng cho điểm tương đương. Nội dung Điểm
Câu I (2,0 điểm) .
1. (1,0 điểm) Rút gọn biểu thức A = 2 3 − 3 27 + 7 7 + 4 3. A = − + ( + )2 2 3 9 3 7 2 3 0,5
A = 2 3 − 9 3 + 7(2 + 3) 0,25 A =14 0,25
2. (1,0 điểm) Cho biểu thức 1 1 x P = − +
(với x ≥ 0, x ≠ 4 ).
2 x − 4 2 x + 4 x − 4
a) (0,5 điểm) Rút gọn biểu thức . P 8 x P = + 0,25 4x −16 x − 4 x + 2 1 P = = 0,25 x − 4 x − 2
b) (0,5 điểm) Tìm tất cả các số nguyên x để P đạt giá trị nguyên.
P đạt giá trị nguyên ⇔ x − 2 = 1 ± 0,25
x − 2 =1 ⇔ x = 3 ⇔ x = 9 (thỏa mãn điều kiện x ≥ 0, x ≠ 4 ). 0,25 x − 2 = 1
− ⇔ x =1 ⇔ x =1(thỏa mãn điều kiện x ≥ 0, x ≠ 4 ).
Câu II (1,5 điểm).
1. (0,75 điểm) Giải phương trình 2
x + 2x −15 = 0. ∆ ' =1+15 =16 > 0 0,25
Phương trình có hai nghiệm phân biệt x = 1 − + 16 = 3 0,25 1 x = 1 − − 16 = 5 − 0,25 2
x(4 − 2y) = 7 + y − 2xy
2. (0,75 điểm) Giải hệ phương trình   x − =  ( y − ) . 2 14 2 3
x(4 − 2y) = 7 + y − 2xy 4x − y = 7 4x − y = 7  ⇔  ⇔  0,25 2x −14 = 2  ( y −3) 2x − 2y = 8 x − y = 4 3  x = 3
⇔ x− y = 4 0,25 x = 1 ⇔  0,25 y = 3 −
Vậy hệ phương trình có nghiệm ( ; x y) = (1; 3 − ) 2
Câu III. (1,5 điểm) Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình 2 y = x ,
đường thẳng (d) có phương trình 2
y = 2x + m − 4m + 9 (với m là tham số) và đường thẳng (∆)
có phương trình y = (a − 3) x + 4 (với a là tham số).
1. (0,5 điểm) Tìm a để đường thẳng (d) và đường thẳng (∆) vuông góc với nhau.
(d) ⊥ (∆) ⇔ 2.(a − 3) = 1 − 0,25 5 ⇔ a = . 0,25 2
2. (1,0 điểm) Chứng minh đường thẳng (d) luôn cắt (P) tại hai điểm phân biệt ,
A B với mọi m .
Gọi A(x ; y , B x ; y (với x < x ), tìm tất cả các giá trị của tham số m sao cho 1 1 ) ( 2 2) 1 2
x − 2023 − x + 2023 = y + y − 48. 1 2 1 2
Phương trình hoành độ giao điểm của đường thẳng (d) và (P) 2 2 2 2
x = 2x + m − 4m + 9 ⇔ x − 2x − m + 4m − 9 = 0( ) 1 0,25
∆ = m − m + = (m − )2 2 ' 4 10 2 + 6 > 0 m ∀ 0,25
Vậy đường thẳng (d) luôn cắt (P) tại hai điểm phân biệt ,
A B với mọi m
a c = −m + m − = −(m − )2 2 . 4 9 2 − 5 < 0 m ∀ ⇒ Phương trình ( ) 1 luôn có hai nghiệm
trái dấu x < 0 < x 1 2 0,25 x − 2023 < 0 1 
⇒ x − 2023 − x + 2023 = − x + x 1 2 ( 1 2) x + 2023 >  0 2
x − 2023 − x + 2023 = y + y − 48 ⇔ −(x + x ) 2 2 = x + x − 48 1 2 1 2 1 2 1 2
⇔ −(x + x ) = (x + x )2 2
− 2x .x − 48 ⇔ 2 − = 2 − 2( 2
−m + 4m − 9 − 48 1 2 1 2 1 2 ) 0,25 m = 6 2
⇔ m − 4m −12 = 0 ⇒  . m = 2 −
Câu IV. (4,0 điểm) Cho đường tròn (O) . Từ điểm M bên ngoài đường tròn kẻ hai tiếp tuyến ,
MA MB với đường tròn (O) ( ,
A B là các tiếp điểm). Lấy điểm C bất kì trên cung nhỏ AB (C
khác A và B ). Gọi D, E, F lần lượt là hình chiếu vuông góc của C trên các AB, AM , BM .
1. (1,0 điểm) Chứng minh tứ giác AECD nội tiếp đường tròn. 3 ⊥ ⇒  DC AD ADC = 90° 0,25 ⊥ ⇒  AE EC AEC = 90° 0,25  +  ADC AEC =180° 0,25
⇒ Tứ giác AECD nội tiếp đường tròn. 0,25
2.(1,0 điểm) Chứng minh rằng  =  CDE C . FD
Tứ giác AECD nội tiếp ⇒  =  CDE CAE. 0,25  + 
CDB CFB =180° ⇒ Tứ giác CDBF nội tiếp ⇒  =  CFD C . BD 0,25 Mà  = 
CBD CAE ( Cùng chắn cung AC ) 0,25 ⇒  =  CDE C . FD 0,25
3.(1,0 điểm) Gọi I là giao điểm của AC và ED , K là giao điểm của CB và DF . Chứng minh CD ⊥ IK.
Tứ giác CDBF nội tiếp ⇒  =  CFD C . BD  = 
CDE CFD (Chứng minh trên) ⇒  =  CDE CBD hay  =  CDI CBA( ) 1 0,25
Tứ giác CDBF nội tiếp  =  CDF CBF Mà  = 
CBF CAB (Cùng chắn cung BC ) ⇒  =  CDK CAB(2)
Từ ( ) ( ) ⇒  +  =  +  +  1 , 2
ICK IDK ICK IDC CDK =  +  +  0 ACB CBA CAB =180 0,25
⇒ Tứ giác CIDK nội tiếp Suy ra  =  CIK CDK Mà  = 
CDK CAB (Chứng minh trên) 0,25 ⇒  =  CIK CAB ⇒ IK // AB
Mà CD ⊥ AB ⇒ CD ⊥ IK. 0,25
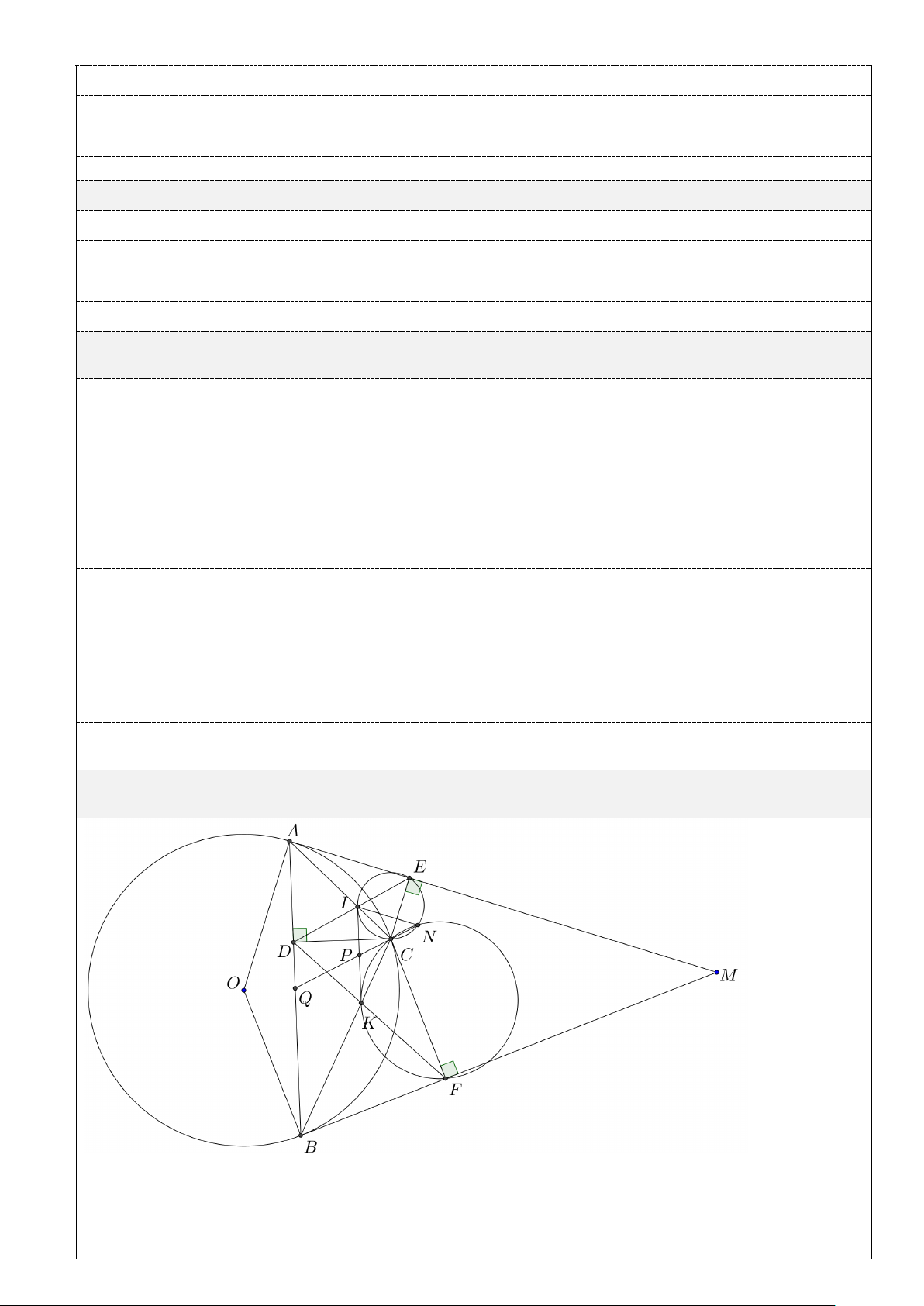
4. (1,0 điểm) Đường tròn ngoại tiếp hai tam giác CIE và CKF cắt nhau tại điểm thứ hai là N .
Chứng minh đường thẳng NC đi qua trung điểm của đoạn thẳng AB .
Gọi NC cắt IK, AB lần lượt tại P,Q  = 
CIK CAB (Chứng minh trên).
Tứ giác AECD nội tiếp đường tròn ⇒  =  CAD CED hay  =  CAB CEI 4 ⇒  =  CEI CIK
⇒ IK là tiếp tuyến của đường tròn ngoại tiếp tam giác CIE
Chứng minh tương tự: IK là tiếp tuyến của đường tròn ngoại tiếp tam giác CKF 0,25
Xét hai tam giác PIC, PNI có  IPN chung,  = 
PIC PNI (cùng chắn cung IC ) 0,25 ⇒ PI ∆ C∽ PN ∆ I PI PC 2 ⇒ =
⇒ PI = PC.PN PN PI Chứng minh tương tự: 2
PK = PC.PN 0,25 Vậy PI = PK IK // AB IP CP PK ⇒ = = AQ CQ QB Mà PI 0,25
= PK ⇒ AQ = QB
Hay Q là trung điểm của AB
Câu V. (1,0 điểm) Cho a,b,c là các số không âm thỏa mãn a + b + c =1011 . Chứng minh rằng: (b − c)2 (c − a)2 (a −b)2 2022a + + 2022b + + 2022c + ≤ 2022 2 2 2 2 Ta có: (b − c)2 (b + c)2 (b + c)2 2022a + = 2022a +
− 2bc ≤ 2022a + (vì bc ≥ 0) 2 2 2 0,25 (b − c)2 ( − a)2 1011 ⇒ 2022a + ≤ 2022a + 2 2 (b − c)2 ( + a)2 1011 ⇒ 2022a + ≤ 2 2 0,25 (b − c)2 + bc  = 0 ⇒ 1011 2022 a a + ≤ dấu = xảy ra ⇔ 2  2
a + b + c = 1011 (c − a)2 Tương tự: 1011 2022 + b b + ≤ 2 2 0,25 (c −b)2 1011 2022 + c c + ≤ 2 2 (b − c)2 (c − a)2 (a −b)2 3.1011 2022 + + 2022 + + 2022
+ a + b + c a b c + ≤ 2 2 2 2 (b − c)2 (c − a)2 (a −b)2 ⇒ 4.1011 2022a + + 2022b + + 2022c + ≤ = 2022 2 2 2 2 2 0,25
a + b + c = 1011 Dấu = xảy ra ⇔ 
ab = bc = ca = 0
(Khi trong ba số a,b,c có một số bằng 1011 và hai số bằng 0).
-----------------Hết-----------------
Document Outline

• Đề toán chính thức ( toán chung) 2023-2024
• Đáp án đề chính thức (toán chung) 2023-2024