Đề tuyển sinh lớp 10 chuyên môn Toán (chuyên) 2022 – 2023 sở GD&ĐT Gia Lai

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH VÀO LỚP 10 CHUYÊN GIA LAI
NĂM HỌC 2022 – 2023 ĐỀ CHÍNH THỨC
Môn thi: TOÁN (Chuyên)
( Đề thi có 01 trang)
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
Họ và tên thí sinh:……………..………………………..……………….; SBD……………….
Câu 1: (2,0 điểm)
a) Xác định tọa độ giao điểm của parabol (P) 2
: y = 3x và đường thẳng (d ) : y = 2x + 8. b) Cho 1 1 1 1 A = + + ++ 1+ 3 3 + 5 5 + 7 2021 + 2023 và 2023 2 2022 B − = . 2 + 5 − 6 + 20 . 4
Không sử dụng máy tính cầm tay, hãy chứng tỏ A > B .
Câu 2: (2,0 điểm) 3
a) Tìm một đa thức bậc ba P(x) với hệ số nguyên nhận 2 4 x + = là một nghiệm và 3 P( ) 1 = 6 − .
b) Tìm nghiệm tất cả các số nguyên x, y thỏa mãn: 2 2 2 2 2
x y − 2x y + 3x + 4xy − 4x + 2y − 4y −1 = 0.
Câu 3: (2,0 điểm)
a) Giải phương trình x + 4 x −3 +1 + x − 4 x −3 +1 = x −11. 8
 xy − x −14y + 4 = 0
b) Giải hệ phương trình  . 2 2 2 8
 x y + 7xy − 20y + 2 = 0
Câu 4: (3,0 điểm)
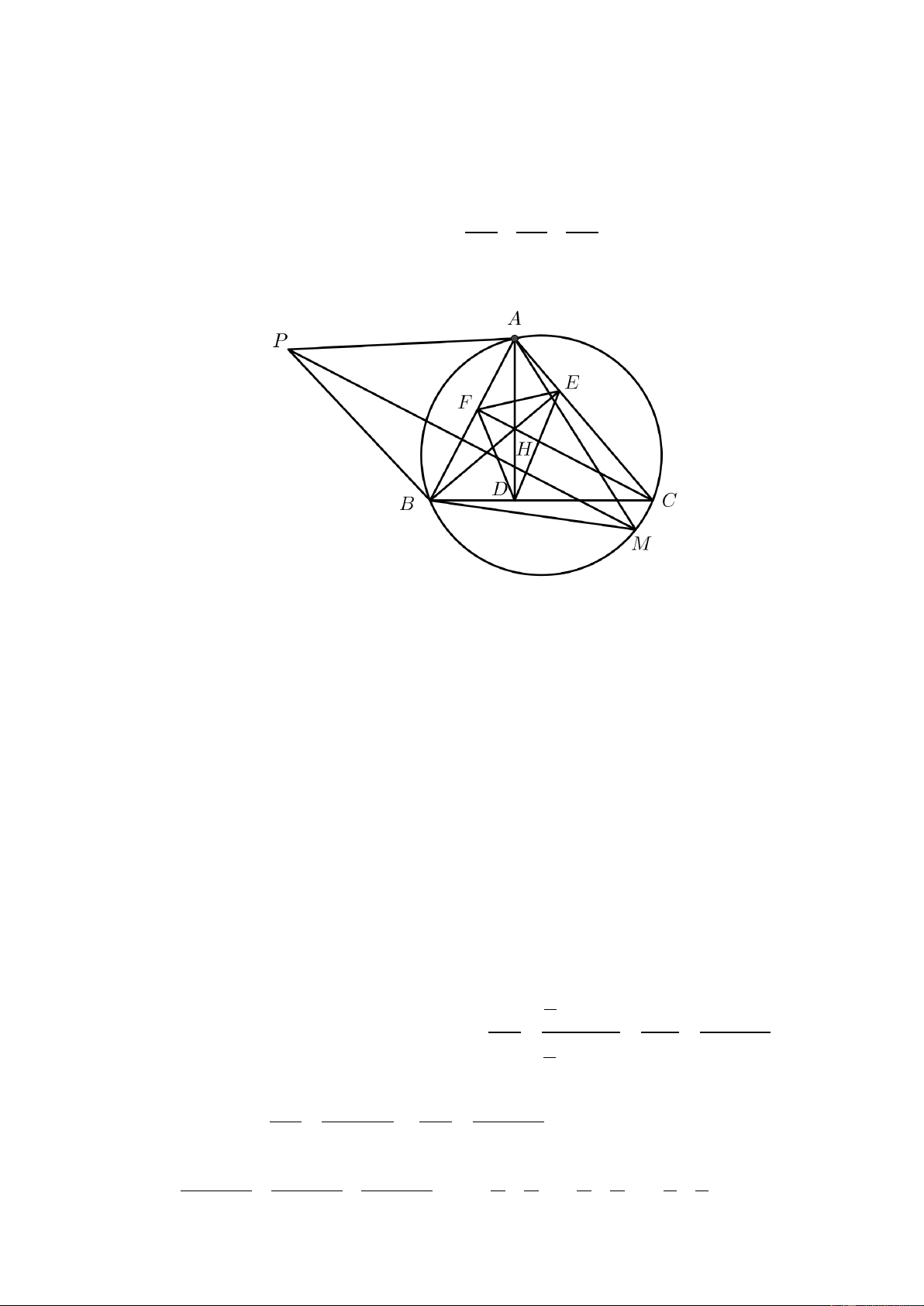
Cho tam giác ABC nội tiếp đường tròn (O) , kẻ ba đường cao AD, BE, CF cắt nhau tại
H , lấy điểm M trên cung nhỏ BC ( M ≠ B, C ). Gọi P là điểm đối xứng với M qua . AB a) Chứng minh:  = 
APB ACB và tứ giác AHBP nội tiếp một đường tròn.
b) Chứng minh: H là tâm đường tròn nội tiếp tam giác FDE .
c) Tìm giá trị nhỏ nhất của biểu thức AD BE CF T = + + . HD HE HF
Câu 5: (1,0 điểm)
Cho các số thực dương x, y, z thoả mãn 1 1 1 + + = 3. Chứng minh rằng x y z 2 2 2
x + y + z − 2xyz ≥1.
------------------HẾT----------------
Chữ ký giám thị 1…………………………… Chữ ký giám thị 2…………………..………………… HƯỚNG DẪN GIẢI
Câu 1: (2,0 điểm)
a) Xác định tọa độ giao điểm của parabol (P) 2
: y = 3x và đường thẳng (d ) : y = 2x + 8. b) Cho 1 1 1 1 A = + + ++ 1+ 3 3 + 5 5 + 7 2021 + 2023 và 2023 2 2022 B − = . 2 + 5 − 6 + 20 . 4
Không sử dụng máy tính cầm tay, hãy chứng tỏ A > B . Lời giải
a) Phương trình hoành độ giao điểm của parabol (P) và đường thẳng (d ) là 2 2
3x = 2x + 8 ⇔ 3x − 2x −8 = 0 (∗). Ta có: ∆′ = (− )2 1 − 3.( 8 − ) = 25 > 0 . ( ) ( )
Suy ra (∗) có hai nghiệm phân biệt: 1 25 x − − + = = 2 và 1 25 4 x − − − = = − . 3 3 3
Với x = 2 thì thay vào phương trình của (P) ta được y =12 . Với 4
x = − thì thay vào phương trình của (P) ta được 16 y = . 3 3
Vậy tọa độ các giao điểm của parabol (P) và đường thẳng (d ) là (2 ;12) và  4 16 ;  −  . 3 3    b) Ta có: 1 n + 2 − n n + 2 − n = = n ∗ ∀ ∈  .
n + n + 2 ( n + 2 + n )( n + 2 − n ) , 2 Do đó, 3 1 5 3 7 5 2023 2021 2023 1 A − − − − − = + + ++ = . 2 2 2 2 2 Mặt khác, 2022 2 2022 1 B − + = . 2 + 5 − 5 + 2 5 +1 4 2  −  =   + − ( + )2 2022 1 . 2 5 5 1  2  2022 −1 = . 2 + 5 − ( 5 + ) 1 2 2022 −1 = . 2 Vì 2023 − − > 2022 nên ta có 2023 1 2022 1 > hay A > B . 2 2
Câu 2: (2,0 điểm) 3
a) Tìm một đa thức bậc ba P(x) với hệ số nguyên nhận 2 4 x + = là một nghiệm và 3 P( ) 1 = 6 − .
b) Tìm nghiệm tất cả các số nguyên x, y thỏa mãn: 2 2 2 2 2
x y − 2x y + 3x + 4xy − 4x + 2y − 4y −1 = 0. Lời giải 3 a) Ta có 2 + 4 3 x =
⇔ 3x − 2 = 4 ⇔ (3x − 2)3 3 2
= 4 ⇔ 27x −18x +12x −12 = 0. 3
Suy ra đa thức bậc ba P(x) thỏa đề có dạng P(x) = k ( 3 2
27x −18x +12x −12) với k là hằng số. Vì P( ) 1 = 6 − nên 3 − k = 6 − ⇔ k = 2.
Vậy có đa thức cần tìm là P(x) 3 2
= 54x − 36x + 24x − 24.
b) Tìm nghiệm tất cả các số nguyên x, y thỏa mãn: 2 2 2 2 2
x y − 2x y + 3x + 4xy − 4x + 2y − 4y −1 = 0. Ta có 2 2 2 2 2
x y − 2x y + 3x + 4xy − 4x + 2y − 4y −1 = 0 ⇔ ( 2 2 2 2
x y − 2x y + x ) + ( 2 2
2x + 4xy + 2y ) − 4x − 4y −1= 0
⇔ (xy − x)2 + 2(x + y)2 − 4(x + y) + 2 = 3
⇔ (xy − x)2 + 2(x + y − )2 1 = 3
Vì x, y là các số nguyên nên ( − )2
xy x và (x + y − )2 1 là các số tự nhiên. (
 xy − x)2 =1   x y −1  = 1 2 2  ( ) 2
Do đó, (xy x) 2(x y ) 1 3  − + + − = ⇔  ⇔  (  x + y − )2 2 1 =1   x +  ( y − )2 1 + 2x( y − ) 1 =1 x  ( y − ) 1 =1 x  ( y − ) 1 = 1 − ⇔  hoặc  . 2 x +  ( y − )2 1 = 1 − 2 x +  ( y − )2 1 = 3
Cả hai trường hợp đều không thỏa mãn.
Vậy không tồn tại các số nguyên x, y thỏa mãn đề bài.
Câu 3: (2,0 điểm)
a) Giải phương trình x + 4 x −3 +1 + x − 4 x −3 +1 = x −11. 8
 xy − x −14y + 4 = 0
b) Giải hệ phương trình  . 2 2 2 8
 x y + 7xy − 20y + 2 = 0 Lời giải
a) Điều kiện: x ≥ 3.
Với điều kiện đó, ta có x + 4 x −3 +1 + x − 4 x −3 +1 = x −11
⇔ x −3+ 4 x −3 + 4 + x −3− 4 x −3 + 4 = x −11
⇔ ( x −3 + 2)2 + ( x −3 − 2)2 = x −11
⇔ x − 3 + 2 + x − 3 − 2 = x −11
Nếu x <11 thì x −11< 0, không thỏa mãn phương trình.
Nếu x ≥11 thì x −3 − 2 > 0 , ta có
x − 3 + 2 + x − 3 − 2 = x −11
⇔ 2 x − 3 = x −11 2
⇔ x − 26x +133 = 0 x = 7 (ktm)
⇔ x =19(tm)
Vậy phương trình đã cho có nghiệm duy nhất x =19. 8
 xy − x −14y + 4 = 0 b) Ta có  . 2 2 2 8
 x y + 7xy − 20y + 2 = 0
Nếu y = 0 thì không thỏa mãn hệ.  x 4   1  x 8x − −14 + = 0 4 2x + − −14 = 0 (1)  y y    y  y
Nếu y ≠ 0 thì hệ tương đương với  ⇔  . 2  2 x 2   1 8x + 7 − 20 + = 0  x 2 2 2x + − − 20 = 0 (2)  y y     y  y  1 2x + = 1 − 2      y
Trừ (2) cho (1) theo vế ta được 1 1 2 2x + − 4 2x + − 6 = 0 ⇔   .  y     y   1 2x + = 3  y TH1: 1 1 2x + = 1 − ⇔ = 2 − x −1. y y Thay vào (1), ta có 2 1 145 4 x( 2x 1) 14 0 2x x 18 0 x − ± − − − − − = ⇔ + − = ⇔ = . 2 TH1: 1 1 2x + = 3 ⇔ = 2 − x + 3. y y x = 2 Thay vào (1), ta có 2 12 x( 2x 3) 14 0 2x 3x 2 0  − − + − = ⇔ − − = ⇔ 1 . x = −  2
Vậy hệ phương trình đã cho có 4 nghiệm:  1 − − 145 145   − +     ; , 1 145 145  ; − , (2 ; − ) 1 , 1 1 −  ; . 2 145       2 145   2 4 
Câu 4: (3,0 điểm)
Cho tam giác ABC nội tiếp đường tròn (O) , kẻ ba đường cao AD, BE, CF cắt nhau tại
H , lấy điểm M trên cung nhỏ BC ( M ≠ B, C ). Gọi P là điểm đối xứng với M qua . AB a) Chứng minh:  = 
APB ACB và tứ giác AHBP nội tiếp một đường tròn.
b) Chứng minh: H là tâm đường tròn nội tiếp tam giác FDE .
c) Tìm giá trị nhỏ nhất của biểu thức AD BE CF T = + + . HD HE HF Lời giải
a) P đối xứng với M qua AB nên  =  +  =  +  = 
APB APM MPB AMP PMB AMB (1) . Do  AMB và 
ACB là các góc nội tiếp cùng chắn cung AB nên  =  AMB ACB (2) .
Từ (1) và (2) suy ra  =  APB ACB (3) .
Tứ giác DHEC có  = 
HDC HEC = 90° (vì AD, BE là các đường cao của ABC ∆ ) nên  + 
ECD EHD =180°. Suy ra  +  ACB AHB =180° (4).
Từ (3) và (4) suy ra  + 
APB AHB =180° . Do đó, tứ giác AHBP nội tiếp một đường tròn.
b) Dễ thấy, HFAE , AEDB , DBFH là các tứ giác nội tiếp nên  =  =  = 
HFE HAE HBD HFD . Suy ra HF là đường phân giác của tam giác FDE .
Tương tự, HD cũng là đường phân giác của tam giác FDE .
Vậy H là tâm đường tròn nội tiếp tam giác FDE . 1 . AD BC + + c) Đặt S = x S = y S = z . Ta có: AD 2 S x y z ABC = = = . HBC , HCA , HAB HD 1 . S x HBC HD BC 2
Tương tự, ta cũng có: BE x + y + z = ; CF x + y + z = . HE y HF z Suy ra
x + y + z x + y + z x + y + z 3  x y   y z   z x T  = + + = + + + + +      + . x y z
 y x   z
y   x z 
Áp dụng bất đẳng thức AM - GM, ta có: x y + ≥ 2 x y ⋅ = 2; y z + ≥ 2 y z ⋅ = 2; z x + ≥ 2 z x ⋅ = 2 . y x y x z y z y x z x z Suy ra T ≥ 9 .  x y =  y x  AD = 3HD
Đẳng thức xảy ra khi và chỉ khi  y z  x y z 
= ⇔ = = ⇔ BE = 3HE ⇔ H là trọng tâm tam z y  C  F =  3HF  z x  =  x z giác ABC .
Mà H cũng là trực tâm của tam giác ABC nên lúc đó ABC là tam giác đều.
Câu 5: (1,0 điểm)
Cho các số thực dương x, y, z thoả mãn 1 1 1 + + = 3. Chứng minh rằng x y z 2 2 2
x + y + z − 2xyz ≥1. Lời giải
Áp dụng bất đẳng thức AM - GM, ta có: 2 2 2 2 2 2
x + y ≥ 2xy; y + z ≥ 2yz; z + x ≥ 2zx . Suy ra 2 2 2
x + y + z ≥ xy + yz + zx . Ta có: 1 1 1
+ + = 3 ⇔ xy + yz + zx = 3xyz . x y z Do đó, 2 2 2
x + y + z − 2xyz ≥ xyz (1).
Dễ dàng chứng minh bất đẳng thức AM – GM cho ba số không âm a, b, c : 3
a + b + c ≥ abc .
Áp dụng bất đẳng thức này, ta có 1 1 1 1 1 1
3 = + + ≥ 3.3 ⋅ ⋅ ⇔ xyz ≥1 (2) . x y z x y z Từ (1) và (2) suy ra 2 2 2
x + y + z − 2xyz ≥1.
Đẳng thức xảy ra khi x = y = z =1.
Document Outline

• de-tuyen-sinh-lop-10-chuyen-mon-toan-chuyen-2022-2023-so-gddt-gia-lai
• 21. GIA LAI