Đề tuyển sinh lớp 10 chuyên môn Toán (chuyên) năm 2021 – 2022 sở GD&ĐT Lào Cai

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN LÀO CAI NĂM HỌC 2021 – 2022 Môn: Toán (Chuyên 1) ĐỀ CHÍNH THỨC Khóa ngày: 03/06/2021 Đề thi gồm có 01 trang
Thời gian: 150 phút (không kể giao đề) Câu 1. (2,0 điểm)
 a a 1 a a 1  a  2  a) Cho biểu thức A     :   
 với a  0; a  1; a  2 . Tìm tất cả các giá trị a  a a   a   a  2 
nguyên dương của a đề P nhận giá trị nguyên.
b) Cho x  1 2021 . Tính giá trị biểu thức: 5 4 3 2
x  2x  2021x  3x  2018x  2021. Câu 2. (2,5 điểm)
1) Một người dự định đi xe đạp từ A đến B cách nhau 40km trong một thời gian nhất định. Sau khi đi
được 20km người đó đã dừng lại nghỉ 20 phút. Do đó để đến B đúng thời gian dự định người đó phải tăng
vận tốc thêm 3km/h. Tính vận tốc dự định của người đó. 2) Cho phương trình 2 x  2m  
1 x  2m  5  0 (trong đó m là tham số).
a) Chứng minh rằng phương trình luôn có 2 nghiệm x ; x với mọi m. 1 2
b) Tìm tất cả các giá trị của m để phương trình có 2 nghiệm x ; x thỏa mãn điều kiện: 1 2
 2x 2mx 2m 1 2x  mx  m  1 1 2 2 2 2 1 0. Câu 3. (3,5 điểm)
Cho tam giác nhọn  ABC không cân (AB < AC) có đường tròn ngoại tiếp (O; R) và đường tròn nội
tiếp (I; r). Đường tròn (I; r) tiếp xúc với các cạnh BC , CA, AB lần lượt tại D, E, F. Kéo dài AI cắt BC tại M
và cắt đường tròn (O;R) tại điểm thứ 2 là N (N khác A). Gọi Q là giao điểm của AI và FE. Nối AD cắt đường
tròn (I; r) tại điểm thứ 2 là P (P khác D). Kéo dài DQ cắt đường tròn (I; r) tại điểm thứ 2 là T (T khác D). Chứng minh rằng: a) 2 AF  A . P AD
b) Tứ giác PQID nội tiếp và 2 NB  NM .N . A
c) QA là phân giác của  PQT d)  ADF   QDE Câu 4. (2,0 điểm) 2 1 1
a) Cho hai số thực dương ;
x y thỏa mãn: x  y  . Tìm giá trị nhỏ nhất của A  53x  53y   . 3 2 2 x y
b) Cho ba số thực dương ; x y , z thỏa mãn: 2 2 2
x  y  z  3 . Chứng minh rằng:  4 4 4 x  y  z    3 3 3
x  y  z   3 x  y  z . Câu 5. (1,0 điểm)
a) Tìm tất cả các bộ số nguyên  x ; y thỏa mãn phương trình: 2 2
x  2x  2y  2 xy   1
b) Cho p là số nguyên tố sao cho tồn tại các số nguyên dương x ; y thỏa mãn 3 3 x  y  p  6xy  8.
Tìm giá trị lớn nhất của p .
--------------------- HẾT ---------------------
HƯỚNG DẪN GIẢI ĐỀ THI TUYỂN SINH LỚP 10 THPT CHUYÊN – LÀO CAI (2021-2022) Câu 1. (2,0 điểm)
 a a 1 a a 1  a  2  a) Cho biểu thức A     :   
 với a  0; a  1; a  2 . Tìm tất cả các giá trị a  a a   a   a  2 
nguyên dương của a đề P nhận giá trị nguyên.
b) Cho x  1 2021 . Tính giá trị biểu thức: 5 4 3 2
x  2x  2021x  3x  2018x  2021. Lời giải: a  0  a) Với:  a   1,  2   a a  a a    a  
 a  1a a  1  a  1a a  1 1 1 2  a  2  Ta có: A   :      a  a a   a   a    a a a a a            1    : 2 1    2  
 a  a 1 a  a 1  a  2   a  2  2a  4 8 A     :  2   2         a a   a  2   a  2  a  2 a  2 8 Để A   2 
  a  2U 8 1; 2; 4;  8 a  2  a Do: 
 a  2  5  a  2  8  a 6 TM  a   1;  2 Vậy a  6  A  b) Đặt: 5 4 3 2 5 4 3 3 2 2
M  x  2x  2021x  3x  2018x  2021  x  2x  2020x  x  2x  2020x  x  2x  2020 1. 3 M  x  2 x  x   x 2x  x   2x  x   2x  x  3 2 2020 2 2020 2 2020 1 2 2020 x  x   1 1 Mà: x    x    x  2 2 1 2021 1 2021
1  2021  x  2x  2020  0.  M  1 Câu 2. (2,5 điểm)
1) Một người dự định đi xe đạp từ A đến B cách nhau 40km trong một thời gian nhất định. Sau khi đi
được 20km người đó đã dừng lại nghỉ 20 phút. Do đó để đến B đúng thời gian dự định người đó phải tăng
vận tốc thêm 3km/h. Tính vận tốc dự định của người đó. 2) Cho phương trình 2 x  2m  
1 x  2m  5  0 (trong đó m là tham số).
a) Chứng minh rằng phương trình luôn có 2 nghiệm x ; x với mọi m. 1 2
b) Tìm tất cả các giá trị của m để phương trình có 2 nghiệm x ; x thỏa mãn điều kiện: 1 2
 2x 2mx 2m 1 2x  mx  m  1 1 2 2 2 2 1 0. Lời giải:
1) Gọi vận tốc dự định của xe đạp là: x km / h; x 0.
Vận tốc sau khi tăng tốc là: x  3 km / h. 40 Thời gian dự định là: h. x
Quãng đường từ lúc tăng tốc là: 40  20  20 km. 20
Thời gian lúc chưa tăng tốc là: h. x 20
Thời gian từ lúc tăng tốc là: h. x  3 20 1 20 40 x  12 TM  Theo đề bài ta có:      x 3 x  3 x x  1  5  KTM 
Vậy vận tốc dự định của xe đạp là: 12 (km/h) 2) a) Ta có:     m   2 2 '
1   2m  5  m  4m  6  
m  22  2  0 m
=> Phương trình luôn có 2 nghiệm phân biệt với mọi m. x  x  m  1 2 2 1 b) Theo Vi-et ta có:  x x  2m  5  1 2 Do: 1 x ; 2
x là nghiệm của phương trình nên ta có: 2 x  2m   2 2 x  m  
x  mx  x  m    x  mx  m    1 1 1 2 5 0 1 2 1 2 1 2 1 4 0 1 2 1 2 1 4 2 1    x      2 x  2m   2 2 x  m  
x  mx  x  m    x  mx  m    2 1 2 2 5 0 2 2 2 2 2 2 1 4 0 2 2 2 2 1 4 2 2    x Mà:  2 x  2mx  2m   1  2 x  mx  m     x  x    x  x  x x  1 1 2 2 2 2
1 0 4 2 14 2 2 0 16 8 1 2 4 1 2 0   m   m   3 16 8.2 1 4 2
5  0  12  8m  0  m  2 Câu 3. (1,0 điểm)
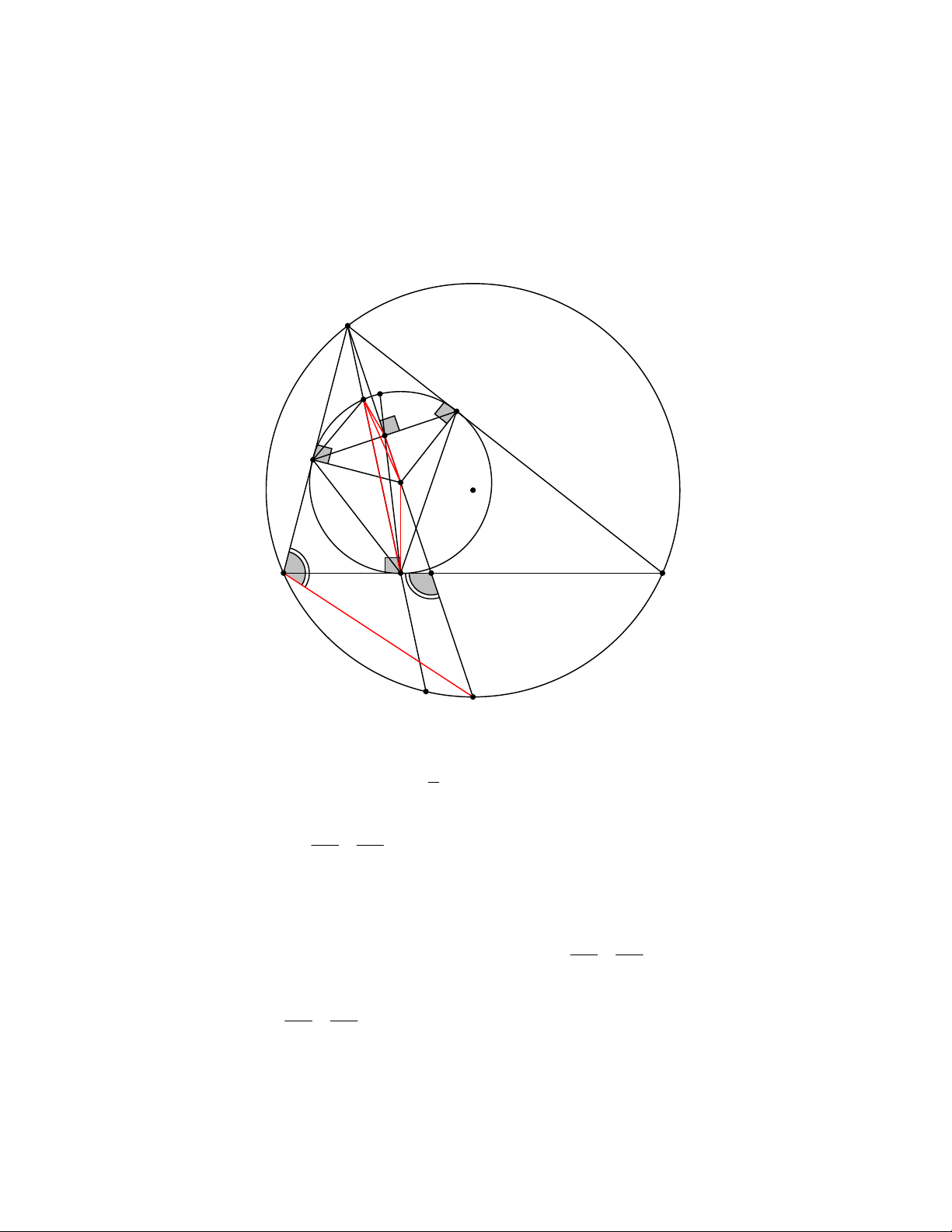
Cho tam giác nhọn  ABC không cân (AB < AC) có đường tròn ngoại tiếp (O; R) và đường tròn nội
tiếp (I; r). Đường tròn (I; r) tiếp xúc với các cạnh BC , CA, AB lần lượt tại D, E, F. Kéo dài AI cắt BC tại M
và cắt đường tròn (O;R) tại điểm thứ 2 là N (N khác A). Gọi Q là giao điểm của AI và FE. Nối AD cắt đường
tròn (I; r) tại điểm thứ 2 là P (P khác D). Kéo dài DQ cắt đường tròn (I; r) tại điểm thứ 2 là T (T khác D). Chứng minh rằng: a) 2 AF  A . P AD
b) Tứ giác PQID nội tiếp và 2 NB  NM .N . A
c) QA là phân giác của  PQT d)  ADF   QDE Lời giải: A 1 2 T P E Q F O I 2 B C 1 D M N 1
a) Xét  AFP và  ADF có:  AFP   ADF   FP ;  A Chung 2
  AFP ∽  ADF g g AF AP 2 .    AF  A . P AD (đpcm) AD AF
b) Vì: AF và AE là 2 tiếp tuyến của I   AI là trung trực của FE  AI  FE tại Q. AP AI 2  A F  A .
Q AI (hệ thức lượng)  AQ AI  AP AD  2 . .  A F    AQ AD AP AI Xét  APQ và  AID có:  cmt;  A Chung AQ AD
  APQ ∽  AID  .cg .c   AQP  
ADI  PQID nội tiếp (vì: 
AQP là góc ngoài tại đỉnh Q) Ta có:  A    NB  NC  B  1 2
A (vì: AI là tia phân giác)     A 1 2
Xét  ABN và  BMN có:  B   A cmt;  N Chung 1 2
  ABN ∽  BMN g g AN BN 2 .    NB  N . A NM (đpcm) BN MN  IPD   IDP IP  ID  r  c) Ta có:    IDP    IQD IPD   1 IQD       ID    2    IDP    AQP cmt Mà:    AQP   AQT   đpcm  AQT    IQD doi dinh
d) Gọi K là giao điểm của AI với I    FK   EK Mà:  AQP   AQT cmt    KP   KT   FP   T E   FDP   EDT  đpcm Câu 4. (2,0 điểm) 2 1 1
a) Cho hai số thực dương ;
x y thỏa mãn: x  y  . Tìm giá trị nhỏ nhất của A  53x  53y   . 3 2 2 x y
b) Cho ba số thực dương ; x y , z thỏa mãn: 2 2 2
x  y  z  3 . Chứng minh rằng:  4 4 4 x  y  z    3 3 3
x  y  z   3 x  y  z . Lời giải: 1 1 CoSi 1 1 a) Dự đoán điểm rơi: 3 2 x  y    ax  ax  3.3 ax ax  3. a   ax  a  27 2 2 2 3 x x x 1 1  1   1  Ta có: A  53x  53y    27x  27x      27 y  27 y     x  y 2 2 2 2 x y  x   y  CoSi 1 1 2 160  A  3.3 27x 27x   3.3 27 y 27 y 
  x  y  27  27  x  y  54   2 2 x y 3 3 1
Dấu “=” xảy ra khi x  y  3 160 1 Vậy  Min A   x  y  3 3 b) Ta có: 4 4 2 4 4 2 4 4 2
x 1  2. x .1  2x ; y 1  2. y .1  2y ; z 1  2. z .1  2z 4 4 4  x  y  z   2 2 2
x  y  z    VT   2 2 2 x  y  z  3 3 3 2 3 2  3  x  y  z Tương tự: 3 3 2 3 3 2 3 3 2
x  x  2. x . x  2x ; y  y  2. y . y  2y ; z  z  2. z . z  2z 3 3 3  x  y  z   2 2 2
x  y  z x  y  z  VT   2 2 2
x  y  z  x  y  z   2 2 2 2 2 2 x  y  z  3  VT   2 2 2
x  y  z x  y  z   2 2 2 x  y  z    2 2 2 3 3
x  y  z x  y  z  3.33  VT   2 2 2
x  y  z  x  y  z  6 Mà: 2 2 2 2 2 2
x 1  2. x .1  2x ; y 1  2. y .1  2y ; z 1  2. z .1  2z 2 2 2
 x  y  z  2 x  y  z 3  VT  2x  y  z  3x  y  z  6 x  y  z  3 (đpcm) Câu 5. (1,0 điểm)
a) Tìm tất cả các bộ số nguyên  x ; y thỏa mãn phương trình: 2 2
x  2x  2y  2 xy   1
b) Cho p là số nguyên tố sao cho tồn tại các số nguyên dương x ; y thỏa mãn 3 3 x  y  p  6xy  8.
Tìm giá trị lớn nhất của p . Lời giải: a) Ta có: 2 2
x  x  y   xy   2 2 2 2 2 2 2 2
1  x  2x  2y  2xy  2  x  2xy  y  y  2x  2  x  y2 2
 2x  y  2y 1 2y  3  x  y2  2x  y   y  2
1  3   x  y2  2 x  y 1  y  2 1  4
 x  y  2   y  2   2 2 1 1 4  0  2  x  y 1  0 x  y 1  0 y 1  0 y 1  0          y 1  2  y 1  2 x  y 1  2 x  y 1  2 x  4 x  0  y  1 y  1          y  3  y  1 x  0 x  4
Vậy  x ; y  4 ; 3 ; 0;  1 ; 0 ;  1 ; 4 ;  1 . b) Ta có: 3 3 3 3
x  y  p  6xy  8  p  x  y  6xy  8  p  x  y3  3xy  x  y  6xy  8
 p  x  y3    xy x  y    p  x  y   x  y2 8 3 2 2
 2x  y  4 3     xy x  y  2 1
Do p là số nguyên tố nên: 
  x  y2  2x  y  4 3xy 1
x  y2  2x  y 43xy 1 (Vì: x; 
y    x  y  2  4 )
 x  y2  x  y 2 2 2 2 2
 4  3xy 1  x  2xy  y  2x  2y  3xy  3  x  xy  y  2x  2y  3 2 2
 x  xy  y  x  y     x  y2 2 4 4 4 8 8 12 2
 3y  42x  y  4 12y 12  4
  x  y  2   y  2   2 2 2 2 3 2 4  1  3.1  2x  y  2  1 2x  y  2  1 2x  y  2  1 2x  y  2  1           y  2  1  y  2  1   y  2 1  y  2  1  x  3 x  2 x  2 x  1          y  3  y  1  y  3  y  1 x  3 TH1:   p  8 KTM   y  3 x  2 TH2:   p  5 TM   y  1 x  2 TH3:   p  7 TM   y  3 x  1 TH4:   p  4 KTM   y  1
Vì: p là số nguyên tố lớn nhất  p  7
Vậy p  7 thỏa mãn yêu cầu bài toán.
__________ THCS.TOANMATH.com __________