Đề tuyển sinh lớp 10 chuyên môn Toán (chuyên) năm 2021 – 2022 sở GD&ĐT Vĩnh Long

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 CHUYÊN TỈNH VĨNH LONG Năm học: 2021 - 2022 Môn thi: TOÁN ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 120 phút
(Không kể thời gian phát đề) Câu 1. (2,0 điểm) x 2x  x x x 1 a) Cho biểu thức A   và B 
1 với x  0, x  1. Rút gọn A và chứng x 1 x  x x 1 minh B > A. b) So sánh 24  26 và 10. Câu 2. (1,0 điểm) Cho Parabol (P): 2
y  x và đường thẳng (d): y  m  
1 x  m  4 (m là tham số). Tìm m để (d) cắt
(P) tại 2 điểm nằm về 2 phía của trục tung. Câu 3. (1,5 điểm)
a) Giải phương trình: 43  x  x 1  x 1  x    x  y 2
b) Giải hệ phương trình:  y 3 2y    x  y 2 Câu 4. (1,5 điểm)
a) Chứng minh rằng tổng các bình phương của 6 số nguyên liên tiếp không thể là số chính phương.
b) Tìm các nghiệm nguyên dương của phương trình: 2 x y  2xy  y  32x Câu 5. (1,0 điểm) 3
Cho hình vuông ABCD và điểm E trên cạnh BC biết AB = 4cm, BE  BC . Tia Ax vuông góc với AE tại 4 A cắt tia CD tại F. a) Tính diện tích  AEF
b) Gọi I là trung điểm của đoạn thẳng EF, tia AI cắt CD tại K. Chứng minh: 2 AE  KF .CF Câu 6. (2,0 điểm)
Cho O; R và điểm M sao cho OM = 2R. Kẻ các tiếp tuyến MA, MB với O (A, B là các tiếp
điểm). Trên đoạn thẳng AB lấy điểm I (Với AI < BI và I khác A). Qua I vẽ dây CD sao cho IC = ID và C
thuộc cung nhỏ AB. Tiếp tuyến của O tại C cắt OI tại Q. Chứng minh:
a) Tứ giác OCQD nội tiếp được đường tròn.
b)  AMB là tam giác đều. c) OQ  MQ Câu 7. (1,0 điểm) 3  x 6  x
Cho số thực x thỏa mãn 1  x  2 . Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: T   x 3  x
= = = = = = = = = = = = = = = = = = = Hết = = = = = = = = = = = = = = = = = = =
--------------------------------------------
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1. (2,0 điểm) x 2x  x x x 1 a) Cho biểu thức A   và B 
1 với x  0, x  1. Rút gọn A và chứng x 1 x  x x 1 minh B > A. b) So sánh 24  26 và 10. Lời giải x x x x x 2 x   1 2
a) Với x  0, x  1.Ta có: A     x 1 x  x x 1 x  x   1 x 2 x 1 x  2 x 1     x 1 x 1 x 1 x 1 x x  x  1x x   1 1 và B  1  1  x  x   1 1  x  x x 1 x 1
Ta lại có: B  A  x  x   x    x  x    x  2 1 2 1
1  0 với x  0, x  1.  B  A (đpcm) b) Ta co:   2 2 24 26
 24  26  2. 24.26  50  2. 624  50  2. 625  100 10  24  26  10 Câu 2. (1,0 điểm) Cho Parabol (P): 2
y  x và đường thẳng (d): y  m  
1 x  m  4 (m là tham số). Tìm m để (d) cắt
(P) tại 2 điểm nằm về 2 phía của trục tung. Lời giải
Xét PT hoành độ giao điểm: 2 x  m   2
1 x  m  4  x  m   1 x  m  4  0 *
Ta có:   m  2  m   2  m  m   m    2 1 4 4 2 1 4 16 m  2m   1 16  m  2 1 16  0  m
 pt (*) luôn có 2 nghiệm phân biệt hay (d) luôn cắt (P) tại 2 điểm phân biệt m x  x  m 1 Theo Vi-et ta có: 1 2  x x  m   1 2 4
Để (d) cắt (P) tại 2 điểm nằm về 2 phía của trục tung thì pt (*) luôn có 2 nghiệm phân biệt trái dấu hay:
m  4  0  m   4 Câu 3. (1,5 điểm)
a) Giải phương trình: 43  x  x 1  x 1  x    x  y 2
b) Giải hệ phương trình:  y 3 2y    x  y 2 Lời giải
a) ĐK: 43  x  0  x  43 x 1 0  x 1 1    x  43 1    x  43  Phương trình          x  43  x   x   7 2 2 2 1
43 x  x  2x 1 x  x  42  0   x  7  x  6  0 b) ĐK: x  y  2x 2x   1  x  y 2
 x  x  y  2x  1   x  y   1 Hệ phương trình     2  y 4 y  
 y  x  y  2y  3 x  y 2 4 3  x  y
Cộng vế với vế của (1) với (2) ta được: 2x  x  y  2x  4y  x  y  2y  2 x  y x  y  0 x  y KTM 
 2x  yx  2y  0     x  2y  0 x  2  y TM  2y 1 7 7  Với x  2  y  2  y    y   x  3  y 2 12 6  7 x   Thử lại ta thấy 6  TM  7  y   12  7 x  
Vậy hệ pt có nghiệm là: 6  7 y   12 Câu 4. (1,5 điểm)
a) Chứng minh rằng tổng các bình phương của 6 số nguyên liên tiếp không thể là số chính phương.
b) Tìm các nghiệm nguyên dương của phương trình: 2 x y  2xy  y  32x Lời giải
a) Giả sử 6 số nguyên liên tiếp lần lượt là: x; x 1; x  2; x  3; x  4; x  5 x Ta có: 2 x   x  2
1  x  22   x  32   x  42   x  52 2 2 2 2 2 2
 x  x  2x 1 x  4x  4  x  6x  9  x  8x 16  x 10x  25 2 2 2 2 2 2
 x  x  2x 1 x  4x  4  x  6x  9  x  8x 16  x 10x  25 2  6x  30x  55 32x b) Ta có: 2
x y  2xy  y  32x  y  2 x  2x   1  32x  y  x  2 1 Do: 
x y   x   x  2  x x     x  2 2 ; 32 1 32 2
1 32x  64x  32  32  x  2 1 32  x  2 1
x  2  U       x  2 1 32 1;2; 4;8;16;32
1  4;16  (Vì:  x  2
1  1 và là số chính phương) x  1 TM 2   TH1:  x   2
1  4  x  2x  3  0    y  8 TM  x  3  KTM  x  3 TM 2   TH2:  x   2
1  16  x  2x 15  0    y  6 TM  x  5   KTM 
Vậy nghiệm của pt là:  ;
x y  1;8 ; 3;6 Câu 5. (1,0 điểm) 3
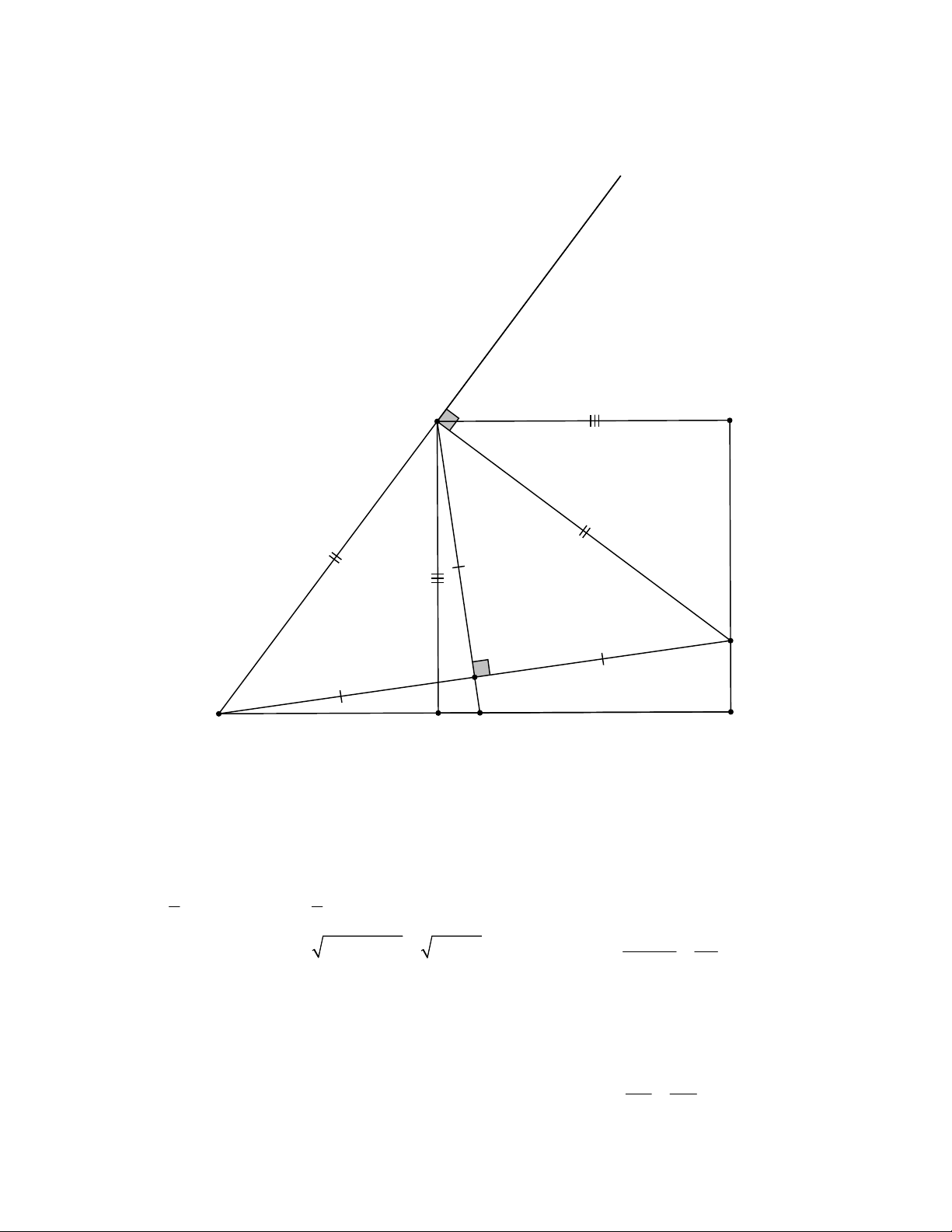
Cho hình vuông ABCD và điểm E trên cạnh BC biết AB = 4cm, BE  BC . Tia Ax vuông góc với AE tại 4 A cắt tia CD tại F. a) Tính diện tích  AEF
b) Gọi I là trung điểm của đoạn thẳng EF, tia AI cắt CD tại K. Chứng minh: 2 AE  KF .CF Lời giải x A B 3 2 1 1 E I 1 F C D K a) Ta có:  A   A (cùng phụ với  A ) 1 3 2  A    A cmt 1 3  
Xét  ABE và  ADF có: 
  ABE   ADF g .c.g   B   D  90  gt 
 AD = AE (2 cạnh tương ứng)   AEF  cân tại A. 3 3
Mà: BE  BC (gt)  BE   4  3cm 4 4 AE.AF 5.5 Theo Pi-Ta-Go ta có: 2 2 2 2
 AE  AB  BE  4  3  5cm  S    12,5 AEF  2 cm  2 2
b) Vì:  AEF  cân tại A (cmt)   E   F  45 1 1
Mà: FI  EI  gt  AI là trung trực của EF  AI  EF   IAE ;  IAF cân tại I.  FI  EI  AI   I   C  90  IF KF
Xét  IKF và  CEF có: 
  IKF ∽ CEF g .g     KF.CF  IF.EF   CF EF  F chung
 KF CF  IF EF  IF  IE 2 2 2 2 . . . 2
 2IE  IE  IA  AE (đpcm) Câu 6. (2,0 điểm)
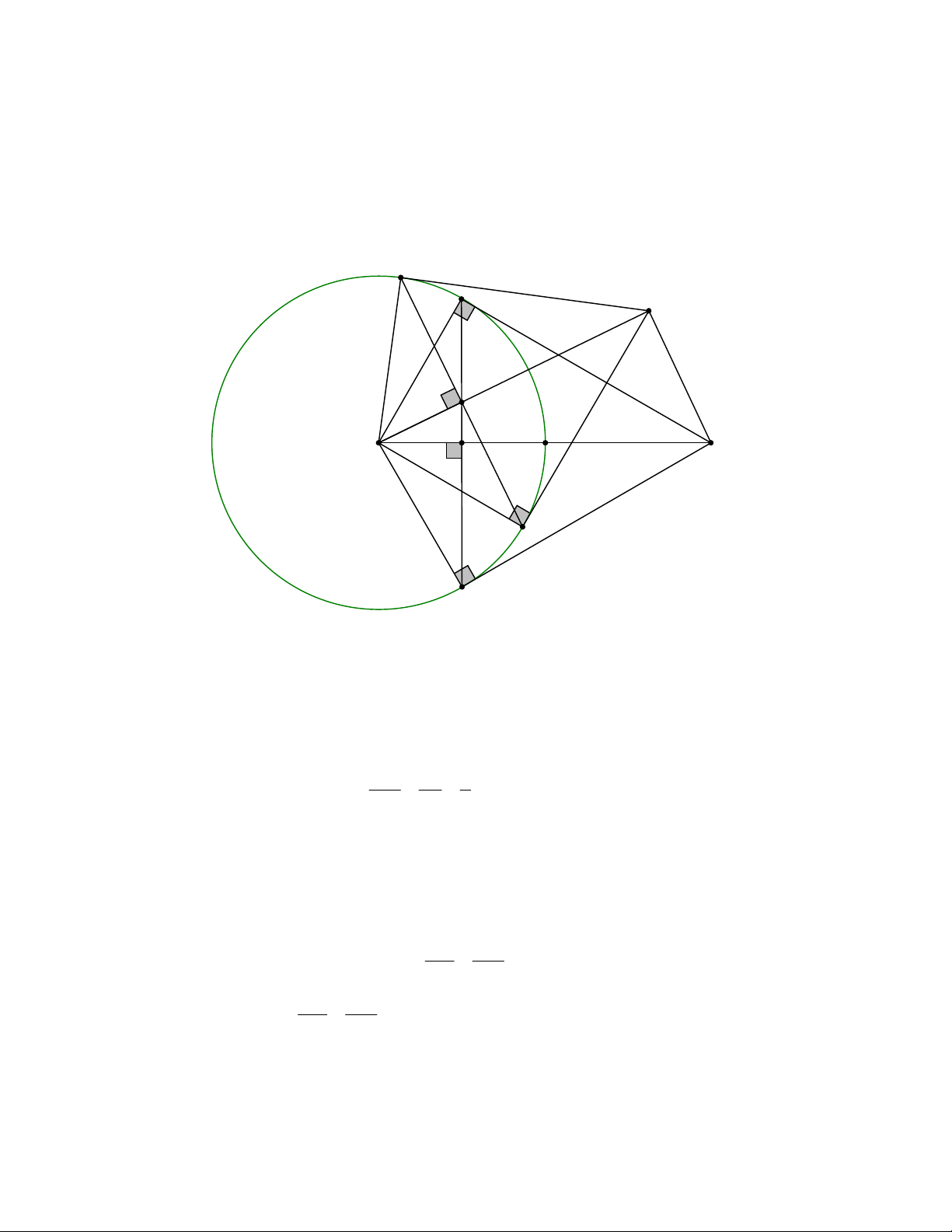
Cho O; R và điểm M sao cho OM = 2R. Kẻ các tiếp tuyến MA, MB với O (A, B là các tiếp
điểm). Trên đoạn thẳng AB lấy điểm I (Với AI < BI và I khác A). Qua I vẽ dây CD sao cho IC = ID và C
thuộc cung nhỏ AB. Tiếp tuyến của O tại C cắt OI tại Q. Chứng minh:
a) Tứ giác OCQD nội tiếp được đường tròn.
b)  AMB là tam giác đều. c) OQ  MQ Lời giải D A Q I 1 O M H 2 C B
a) Ta có: IC  ID  gt  OI  CD tại I (Đường kính vuông góc với dây cung đi qua trung điểm)
 OI là đường trung trực của CD  OQ là đường trung trực của CD  QD  QC
Xét  DOQ và  COQ có: QD  QC cmt ; OC  OD  R  gt ; OQ chung   DOQ =  COQ  . c . c c   OCQ   ODQ  90   OCQ   ODQ  180   DOCQ nội tiếp. OA R 1
b) Xét  AOM  tại A có: sin M      M  30 1 1 M O 2R 2
Gọi H là giao điểm của AB và OM ta có: MA = MB (Tính chất 2 tiếp tuyến cắt nhau)
Mà: OA = OB = R  OM là đường trung trực của AB  OM  AB tại H   HAM  90   M       hay  BAM   1 90 30 60 60
Mặt khác:  ABM cân tại A (Vì: MA = MB)   ABM đều (đpcm)
c) Theo hệ thức lượng trong tam giác vuông ta có: 2 2 OI.OQ  OD  R OI OM  OI.OQ  OH.OM   2 2 OH.OM  OA  R OH OQ OI OM Xét  OHI và  OQM có:  cmt ;  O chung OH OQ   OHI OQM c.g .c   OQM   OHI  90 ∽  OQ  MQ (đpcm) Câu 7. (1,0 điểm) 3  x 6  x
Cho số thực x thỏa mãn 1  x  2 . Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: T   x 3  x Lời giải 3  x 6  x
3 x3 x6 x 2 2 2 x 9  x  6x  x 2x  6x  9 Ta có: T      x 3  x x 3  x 2 2 3x  x x  3x  T  2 x  x 2 2 2
 x  x   Tx  Tx  x  x    T   2 3 2 6 9 3 2 6 9 0
2 x  6  3T  x  9  0   *
Có:     T 2  T   2   T  T  T    2 6 3 4 2 .9 36 36 9 36 72 9 T  8T 12 T  2
Để phương trình (*) có nghiệm thì   0  9 2 T  8T 12 2
 0  T  8T 12  0   T  6 2 2x  6x  9 Với 2 2 T  2 
 2  2x  6x  9  2x  6x   9  0 (vô lý) 2 x  3x 2 2x  6x  9 3 Với 2 2 2 T  6 
 6  2x  6x  9  6x 18x  4x 12x  9  0  x  TM  2 x  3x 2 3  T  6  x  Min 2 2 2x  6x  9 13
Vì: 1  x  2 . Thay x = 2 vào T ta được: T    6,5  2 2 2x  6x  9 13 2 x  3x 2  x  3x 2 x  1 2 2 2 2
 4x 12x 18  13x  39x  9x  27x 18  0  x  3x  2  0   TM  x  2 x  1  T  6,5  Max  x  2
---------------------- THCS.TOANMATH.com ----------------------